馬爾可夫性在獎懲系統中的應用
李慧雪
(浙江財經大學數據科學學院 浙江 杭州 310018)
馬爾可夫性在獎懲系統中的應用
李慧雪
(浙江財經大學數據科學學院 浙江 杭州 310018)
在非壽險精算之中,汽車保險不但是非壽險保險公司的重要業務之一,也是非壽險保險公司盈利的主要方式,如何合理制定保費標準,從而擴大受益至關重要。獎懲系統是馬爾可夫(Markov)過程的一種特殊形式,進行馬爾可夫分析,能夠更好地幫我們評價獎懲系統好壞。本文簡單介紹了Markov鏈的一些基本原理,并在基于汽車保險業務,建立了馬爾可夫獎懲系統,推導了穩態分布和Loimaranta效率表達式,并根據R語言數值模擬結果,對荷蘭許多保險公司所采用的獎懲系統的優劣性進行了評價。
Markov鏈;獎懲系統;穩態分布;Loimaranta效率;數值模擬
現如今我國的保險市場全面放開,各保險公司相互之間的競爭愈發激烈,不斷增強對“獎懲系統”作用的重視[2]。在“獎懲系統”中,“無賠款優待系統”是一種重要的形式,在下一年續保時,對那些無索賠的投保者給以相應的獎勵,而對有過索賠記錄的投保者,在保費上給以相對應的懲罰。作用是讓保險公司收取的保費,更接近于保險指標的風險,激勵發生事故頻率較低的那部分被保險者能夠繼續在同一家公司進行續保[5]。
一、基本概念
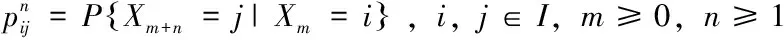
(1.1)
稱πj,j∈I為平穩分布,若它滿足
πj= ∑i∈Iπipij,∑j∈Iπj= 1,πj≥0。 (1.2)
顯然有
(1.3)
其中初始概率為pj=PX0=j,絕對概率為pj(n)=PXn=j。
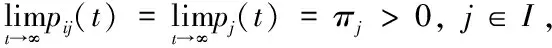
(1.4)

二、獎懲系統模型
在非壽險業務中,汽車保險作為其重要分支之一,在許多國家的總保費收入中占到了最大比例。保險的本質是,“不幸運的”保單持有者的損失由“幸運的”保單持有者所承擔。若保險者想要將這種補貼利益共同體強加給客戶,那么“好的”被保險人會紛紛離去,剩下的只能是“差的”被保險人。經驗費率系統中的獎勵被認為是給予謹慎駕駛員的獎勵,相應地,增加的保費是給予經常發生事故的駕駛員額外增加的罰款。
將獎懲系統引入汽車保險的目的是:1、減少保險公司對于小額度理賠的支出費用;2、在一定程度上,鼓勵被保險者在駕駛車輛時,更加集中注意力,從而主動盡可能減少風險;3、保費負擔公平化,使得被保險人交納的保險費,能夠與其真實的風險水平成比例。另一方面,獎懲系統也有一些缺點,比如:1、被保險者之間的合作互助關系有所減弱了;2、與大數定律相違背,有組織地放棄了保險基本的原則;3、可能破壞了被保險者的經濟穩定性,因為在獎懲系統當中,被保險者在承擔基本保費的同時,還要同時承擔續期保費所存在的變異性。但即使這樣,獎懲系統依然得廣泛應用于實踐當中[4]。
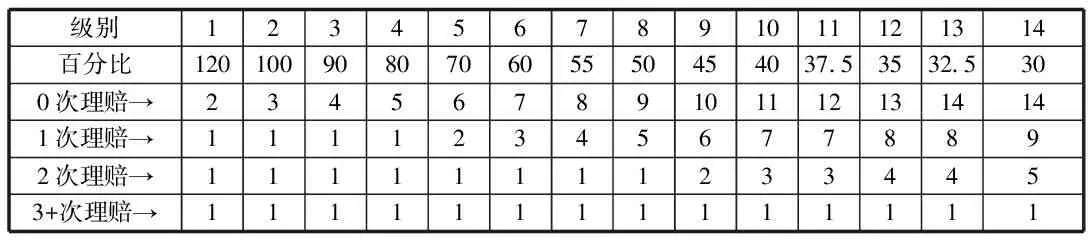
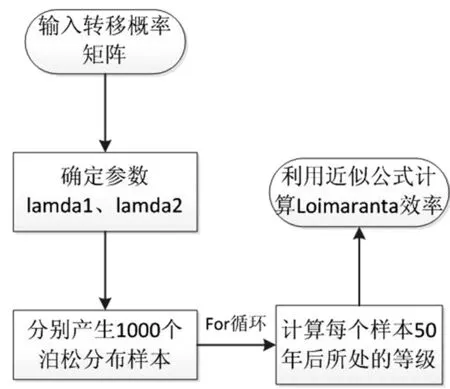
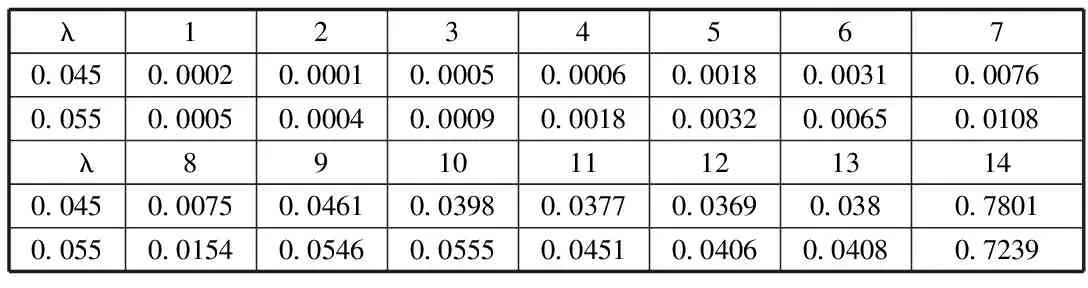
駕駛員本身的狀況稱為自身狀態,假定有n個狀態。設在一個特定的獎懲系統中,有一個駕駛員,若他在第i-1,i年中有理賠記錄,那他在i+1年需要繳納一個較高保費ci+1;若他在第i-1年中有理賠記錄,而在第i年無理賠記錄,或第i年中有理賠記錄而在第i-1年中無理賠記錄,那他在i+1年需要繳納一個保費ci;否則他只需要繳納保費ci-1,ci-1 (一)馬爾可夫分析 定理2[3]存在一個平穩分布是不可約的非周期馬爾可夫鏈是正常返的充要條件,并且這個平穩分布即是極限分布i/μj,j∈I。 因為有限狀態的非周期不可約馬爾可夫鏈有且僅有正的常返態狀態,所以根據定理2知,一定存在一個平穩分布,另一方面獎懲系統之中的馬爾可夫鏈是有限狀態的不可約非周期馬爾可夫鏈,因此該系統中的馬爾可夫鏈一定存在一個平穩分布。 假如一名駕駛員在初始的時刻處在狀態i=1,…,n的概率是PT(0)=(p1,p2,…,pn),則在m個周期之后處于狀態i=1,…,n的概率為PT(m)=PT(0)p(m)=PT(m-1)P。因為平穩分布存在,不妨設π=π1,…,πn,有π=πP,可利用R軟件來計算出該等式的數值解。很明顯,得到的平穩分布為P的特征根等于1所對應的左特征向量。由定理2可得: (2.1) 表示司機從一個狀態i,i=1,2,…,n回到初始狀態所花費的平均時間分別是:μ年。若假定每個保單索賠頻率服從P(λ),對應的穩態概率分布為πi(λ),則其平均獎懲系數就是 (2.2) 該方法的作用在于,能夠找出繳納了高額保費的司機,若按這種狀態進展下去,而加以必要的治理手段,想要讓保費重新達到一個低的狀態幾乎是不可能的,所以必須對其加以干涉,采取各種有效的方式,來改善保費的水平。 設齊次馬爾可夫過程{X(t),t≥0}的狀態空間I={0,1,…},轉移概率為pij(t),如果 (2.3) 則稱{X(t),t≥0} 為生滅過程[8],λi,μi分別稱為出生率和死亡率。由定理1得 (2.4) 逐步遞推得平穩分布 (2.5) 顯然可見平穩分布存在的充要條件是 (2.6) 事實上,上述獎懲系統的生滅過程是在有限狀態之下的,并且λi=c,μi=a,則平穩分布: (2.7) (2.8) 注意: 當市場條件有所變動時,再采用本文方法獲得的結果會和實際差距很大,若隨意采用,就可能出現很大的錯誤,對此必須特別分析討論[6]。 (二)Loimaranta效率 獎懲系統的制定標準是,讓每位保單持有者所交納的保費,最大可能地與其年理賠額的平均值相接近[1]。想要弄清某個獎懲系統能否實現此標準,必須弄明白保費是怎樣依賴于理賠頻率參數λ的。穩定狀態下的保費可表示為b(λ)=π*(c1,…,cn)T,它是在初始狀態影響消失之后,還需交納的平均保費,在一般情況下,此保費應和λ成一定的比例,由于理賠頻率數參數等于λ的駕駛員,他的平均每年的理賠總額會是單個平均理賠額的λ倍,并且在這里已提前規定單個理賠額和理賠頻數無關。 我們稱 (2.9) 為 Loimaranta 效率,由于彈性系數=因變變量的變動比/自變變量的變動比例,因此e(λ)表示穩態保費b(λ)關于λ的彈性。計算彈性時有一種近似的計算方法,首先給定λ的一個值,計算對應b(λ)的值,接著增加一個非常小量Δλ,獲得λ+Δλ,進一步計算b(λ+Δλ),則可得到參數λ的彈性近似值 (2.10) 我們很容易就可以利用R軟件,求得不同取值的λ相對應的彈性系數。對于充分小的h,由泰勒展開可得: b(λ(1+h))≈b(λ)+λh (2.11) (2.12) 所以理想情況下,功效應為e(λ)≈1,功效小于1則表示差駕駛員占便宜。因為穩態保費并不會依賴于初始狀態,因此 Loimaranta 效率也和初始狀態無關,雖然兩者都和理賠頻數λ高度相關。在幾乎所有的系統中,保費的百分比都是一個正的有限數,即b(0)>0,b(∞)<∞,但是大部分的實際獎懲系統中都有b(∞)<∞,因此 (2.13) (2.14) 在本文中,令n代表狀態個數,引入函數tij(k),i,j=1,2,…,n來表示轉移規則,如下: tij(k)=1,如果一年之中有k個理賠,則從狀態i到j; tij(k)=0,else. 當參數為λ時,從狀態i到j的轉移概率為 (3.1) 考慮初始分布l(0)=(l1(0),…,ln(0)),其中lj(0)為在時刻t=0,單個保單處在初試狀態j,j=1,2,…,n的概率;那么在t+1時刻,發現一個駕駛員處在狀態j的概率向量可以由時刻t時地狀態向量l(t)表示如下: (3.2) 對于每一個t,lj(t)的和等于1。對t→∞取極限,可以發現在穩態下: (3.3) 穩態向量l(∞)=(l1(∞),…,ln(∞))是矩陣P,的特征值為1的左特征向量。在穩定狀態之下,可以計算得理賠頻數λ的漸近平均保費[1](穩態保費): (3.4) 其中bj為狀態j時地保費。注意到,lj(∞)依賴于λ,但是不依賴與狀態的初始分布。 如果有一種算法來計算(3.4)式中的b(λ),就能很容易地近似Loimaranta效率e(λ),所要做的就是利用(2.6)式。其實,也有可能精確地計算Loimaranta效率e(λ)。 (3.5) gj(λ)可以通過對方程組(3.3)求導數得到,容易得如下的方程: (3.6) 其中Pij(λ)的導數等于: (3.7) 利用∑jgj(λ)=0這個事實,對每個λ,通過求解所得線性方程組計算Loimaranta效率e(λ)。利用這種方法,我們可以根據效率來比較各個獎懲系統地優劣。 雖然Loimaranta效率e(λ)可以根據公式(3.5)-(3.7),并用近似對λ(1-ε)和λ(1+ε),利用P(210)的任一行計算穩態分布,再利用 (3.8) 計算得到,但在本文中我們利用R語言來模擬得到。 用M個駕駛員在T年后的模擬獎懲位置來估計穩態分布,并由T年支付的平均保費,再用近似的方法得到e(λ)。本文根據荷蘭許多保險公司采用的獎懲標準,來計算其穩態分布和e(λ)。表4.1是該獎懲標準,包括應支付基礎保費的百分比,經過0,1,2,3次或更多次理賠后的轉換情況。在原則上,新來被保險人應該是進入保費水平100%的級別。 表 4.1 數值模擬對應的算法流程圖如圖1: 圖4.1 算法流程圖 從圖1中,我們可以清晰地看到算法的過程,首先輸入轉移概率矩陣,然后根據確定的參數產生泊松分布的樣本,再利用for循環,計算出每個樣本在50年以后所處的等級,最后利用近似公式計算效率值。 表4.2 14個級別的穩態分布 在本文中,取泊松分布參數λ1=0.045,λ2=0.055,駕駛員人數M=10000,年數T=50,通過R語言編程模擬,可以得到14個級別的穩態分布情況如表4.2。觀察表4.2,可以發現穩態分布中,處于等級14的概率最大,分別達到0.7801和0.7239,說明大部分駕駛員在很多年后很有可能只需繳納30%的保費。另外,可以得到Loimaranta效率e(λ)=0.136,值小于1,這表明在該懲罰系統中,資金會從好的駕駛員向差的駕駛員轉移,即該懲罰系統所制定的規則對于差的駕駛員的懲罰力度不夠。 [1]R.卡爾斯等著,唐啟鶴等譯,現代精算風險理論[M].北京:科學出版社,2005:131-143. [2]劉源,徐昕.保險精算中的多零索賠現象探析[J].統計與決策,2008,21:21-23. [3]劉嘉錕,王公恕.應用隨機過程[M].北京:科學出版社,2004. 李慧雪(1995-),女,漢族,碩士研究生,研究方向:生存分析。


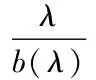
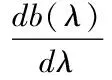
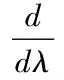


三、模型求解-求穩態保費和Loimaranta效率

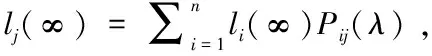
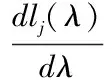

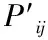
四、數值模擬