T(0,1)模態(tài)導(dǎo)波在彎管上傳播的仿真與實(shí)驗(yàn)

李陽(yáng)，鄒云，張雙楠，蔡桂喜

?

T(0,1)模態(tài)導(dǎo)波在彎管上傳播的仿真與實(shí)驗(yàn)

李陽(yáng)1，鄒云1，張雙楠2，蔡桂喜2

(1. 鄭州大學(xué)機(jī)械工程學(xué)院，河南鄭州 450001；2. 中國(guó)科學(xué)院金屬研究所，遼寧沈陽(yáng) 110016)

由于彎管的幾何形狀復(fù)雜，超聲導(dǎo)波在彎管中的傳播特性比在直管中復(fù)雜。彎管超聲導(dǎo)波檢測(cè)中，衡量其檢測(cè)有效性的一個(gè)重要參數(shù)是透過(guò)率。通過(guò)有限元模擬研究了激勵(lì)頻率、彎曲半徑、彎管角度對(duì)T(0,1)模態(tài)導(dǎo)波透過(guò)率的影響。發(fā)現(xiàn)：不同激勵(lì)頻率的導(dǎo)波在彎管上有不同的透過(guò)率，并且激勵(lì)頻率高的導(dǎo)波由于脈沖寬度小，更易產(chǎn)生新的波前；在不同的彎曲半徑和彎曲角度的彎管中，最小透過(guò)率的T(0,1)模態(tài)導(dǎo)波的頻率也各不一樣；隨彎管角度的變化，信號(hào)的透過(guò)率呈規(guī)律性變化。通過(guò)實(shí)驗(yàn)驗(yàn)證了不同激勵(lì)頻率下，T(0,1)模態(tài)導(dǎo)波透過(guò)率和激勵(lì)頻率的關(guān)系。在實(shí)際檢測(cè)有彎管段的管道時(shí)，需采用多頻率檢測(cè)。

透過(guò)率；彎管；T(0,1)模態(tài)；傳播特性

0 引言

自Gazis[1-2]推導(dǎo)出空心圓管中的導(dǎo)波頻散方程以來(lái)，超聲導(dǎo)波引起了科研人員的極大關(guān)注。導(dǎo)波在直管上的傳播機(jī)制，以及一些特征體對(duì)導(dǎo)波的反射已有了深入研究。近年來(lái)，無(wú)損檢測(cè)儀器公司紛紛推出了各自的導(dǎo)波設(shè)備，使得超聲導(dǎo)波檢測(cè)技術(shù)進(jìn)入了一個(gè)嶄新的階段。但是，一些導(dǎo)波檢測(cè)應(yīng)用難題仍未得到很好的解決，需要更完善的理論指導(dǎo)。如：由于超聲導(dǎo)波在彎管上的傳播特性相對(duì)直管變得復(fù)雜，而導(dǎo)致超聲導(dǎo)波在彎管和過(guò)彎管后的檢測(cè)靈敏度較低。為解決這個(gè)問題，科研人員對(duì)此進(jìn)行了大量的研究。國(guó)外，Takahiro Hayashi[3]等在準(zhǔn)柱坐標(biāo)系上建立了彎管有限元模型，利用半分析有限元方法模擬了導(dǎo)波在彎頭的傳播過(guò)程，減少了計(jì)算時(shí)間。A Demma[4]等將彎管視為圓環(huán)的一部分，利用有限元方法計(jì)算了頻率和速度的關(guān)系，畫出了彎管的頻散曲線，發(fā)現(xiàn)導(dǎo)波經(jīng)過(guò)彎管后的透過(guò)率和管子的形狀、激勵(lì)導(dǎo)波的頻率等因素有關(guān)。R M Sanderson[5]等將經(jīng)過(guò)彎管后的信號(hào)看成是進(jìn)入彎管前直管上的信號(hào)與彎管結(jié)構(gòu)響應(yīng)函數(shù)的卷積，利用有限元方法分析了不同彎管的響應(yīng)函數(shù)。Hideo Nishino[6]等利用寬頻激光超聲激勵(lì)導(dǎo)波，研究了縱向模態(tài)L(0,1)導(dǎo)波在彎管中轉(zhuǎn)換為彎曲模態(tài)F(1,1)的現(xiàn)象，彎管的彎曲角度越大，模態(tài)轉(zhuǎn)換得越嚴(yán)重。國(guó)內(nèi)，周邵萍[7]等人研究了縱向模態(tài)L(0,2)超聲導(dǎo)波在90°彎管中的傳播特性，并分析了L(0,2)模態(tài)超聲導(dǎo)波對(duì)彎管內(nèi)缺陷的檢測(cè)敏感性，發(fā)現(xiàn)彎頭外側(cè)的缺陷更易被檢測(cè)到；并建議采用多個(gè)頻率進(jìn)行實(shí)際檢測(cè)。鄧菲[8]等人采用激勵(lì)寬頻導(dǎo)波的研究方法，可快速選擇出管狀結(jié)構(gòu)檢測(cè)的最優(yōu)導(dǎo)波模態(tài)和激勵(lì)頻率，這可為彎管檢測(cè)中最優(yōu)激勵(lì)頻率的選取提供參考。王悅民[9]等人利用磁致伸縮導(dǎo)波檢測(cè)技術(shù)，發(fā)現(xiàn)彎管中的導(dǎo)波能量的衰減與激勵(lì)頻率存在密切聯(lián)系。

通過(guò)以上研究可知，導(dǎo)波在彎管中的傳播過(guò)程比較復(fù)雜，具有特殊的傳播特性，如：模態(tài)轉(zhuǎn)變、能量集中、透過(guò)率變化等。其中，彎管上導(dǎo)波的透過(guò)率[4]定義為：特定模態(tài)導(dǎo)波經(jīng)過(guò)彎管后橫截面上該模態(tài)合成信號(hào)的峰-峰值除以過(guò)彎管前信號(hào)的峰-峰值。通過(guò)導(dǎo)波的透過(guò)率，可反映出導(dǎo)波對(duì)彎管后缺陷的檢測(cè)靈敏度。因此，彎管超聲導(dǎo)波檢測(cè)中，衡量其檢測(cè)有效性的一個(gè)重要參數(shù)是透過(guò)率。由于T(0,1)模態(tài)導(dǎo)波無(wú)頻散，且T(0,1)模態(tài)導(dǎo)波的質(zhì)點(diǎn)振動(dòng)只包含周向分量而不含徑向和軸向分量，所以在檢測(cè)有液體浸沒的管道或運(yùn)輸液體的管道時(shí)，T(0,1)模態(tài)導(dǎo)波衰減小，傳播距離遠(yuǎn)，因此T(0,1)模態(tài)是應(yīng)用最為廣泛的導(dǎo)波檢測(cè)模態(tài)之一[10]。為利用T(0,1)模態(tài)導(dǎo)波檢測(cè)有彎管段的管道，需要清楚地了解影響導(dǎo)波在彎管上透過(guò)率的因素，并觀察導(dǎo)波在彎管中的傳播現(xiàn)象。

本文通過(guò)一系列有限元模擬和實(shí)驗(yàn)，研究T(0,1)模態(tài)導(dǎo)波在彎管上透過(guò)率的變化規(guī)律，并找出影響導(dǎo)波透過(guò)率的因素，以此來(lái)指導(dǎo)超聲導(dǎo)波在工程檢測(cè)中激勵(lì)頻率的選擇。首先，利用有限元方法模擬激勵(lì)頻率、彎曲半徑和彎曲角度對(duì)T(0,1)模態(tài)導(dǎo)波經(jīng)過(guò)彎管后透過(guò)率的影響。然后，通過(guò)實(shí)驗(yàn)驗(yàn)證在不同的激勵(lì)頻率下，導(dǎo)波透過(guò)率與激勵(lì)頻率的關(guān)系。

1 有限元模擬

1.1 有限元模型

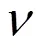
圖1 彎管模型示意圖。其中，A-A和B-B為接收位置，R為彎曲半徑，θ為彎曲角度。橫截面上任意質(zhì)點(diǎn)的三個(gè)位移分量：Da為軸向位移，Dc為周向位移，Dr為徑向位移。

Fig.1 Geometry of the FE model, where the position A-A and B-B are the receiving points, R represents bend radius and θ represents bend angle. Three displacement components of each node on the cross section: Da represents axial displacement, Dc represents circumferential displacement and Dr represents radial displacement

管上每點(diǎn)的振動(dòng)可分解為三個(gè)分量：周向位移、徑向位移和軸向位移，其中周向位移和徑向位移在質(zhì)點(diǎn)所在橫截面的面內(nèi)，周向位移垂直于半徑方向，徑向位移與半徑方向重合，軸向位移方向垂直于橫截面與管的軸向平行。在圖1管子的激勵(lì)端所有節(jié)點(diǎn)上，加載相同的周向位移載荷信號(hào)，信號(hào)為加漢寧窗的5周期正弦函數(shù)信號(hào)，以激勵(lì)出特定頻率的T(0,1)模態(tài)導(dǎo)波。在兩個(gè)接收位置A-A和B-B的管壁上，均勻分布12個(gè)點(diǎn)接收周向位移導(dǎo)波信號(hào)，如圖1所示。規(guī)定：點(diǎn)1對(duì)應(yīng)的角度為180°，點(diǎn)4對(duì)應(yīng)的角度為90°，點(diǎn)7對(duì)應(yīng)的角度為0°，點(diǎn)10對(duì)應(yīng)的角度為-90°。

1.2 激勵(lì)頻率與透過(guò)率的關(guān)系

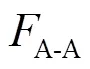
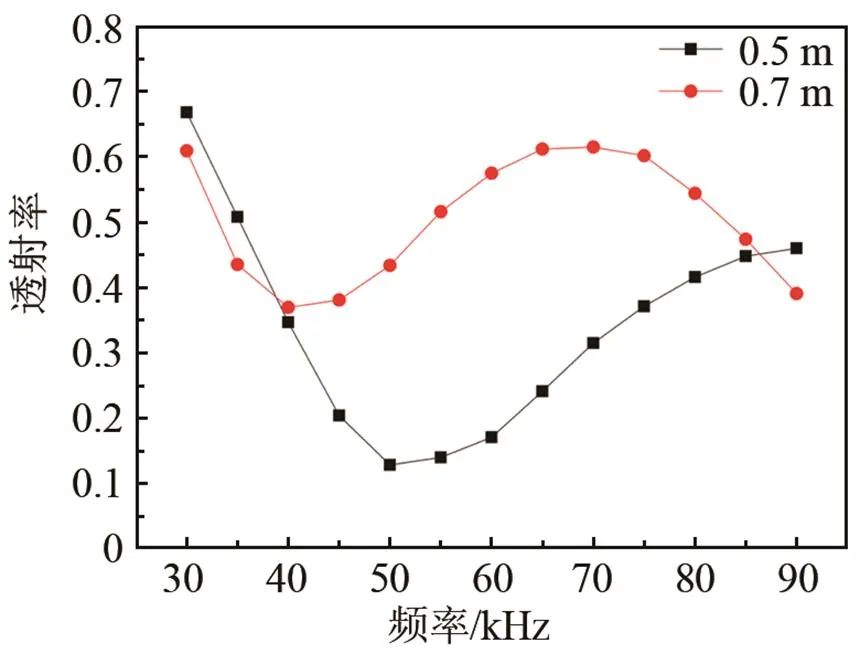
圖2 在彎曲角度90°、彎曲半徑分別為0.5 m和0.7 m的彎管上，T(0,1)模態(tài)導(dǎo)波經(jīng)過(guò)彎管的透過(guò)率與激勵(lì)頻率的關(guān)系

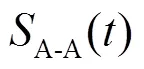
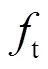
(a) 彎曲半徑為0.7 m

(b) 彎曲半徑為0.5 m

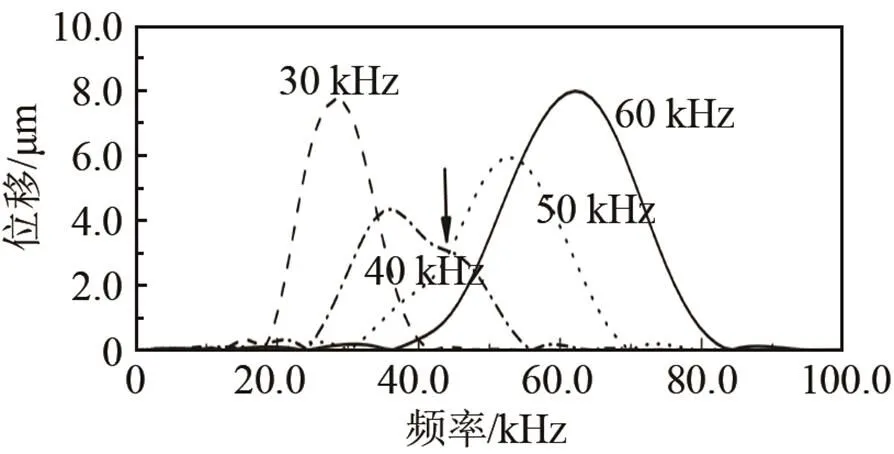
圖3 不同激勵(lì)頻率下，T(0,1)導(dǎo)波的頻域信號(hào)

Fig.3 Frequency spectrums of receiving mode T(0,1) after propagating through bends with (a) 0.7 m and (b) 0.5 m at different excitation frequencies

根據(jù)Brath[13]等人和Qi[14]等人的研究，導(dǎo)波在彎管中傳播一定距離后會(huì)產(chǎn)生新的波前，這是由于彎管的外側(cè)傳播距離長(zhǎng)、內(nèi)側(cè)傳播距離短，內(nèi)側(cè)波前向外側(cè)擴(kuò)展，傳播一定距離后形成新的波前。將激勵(lì)頻率提高到150 kHz，在彎曲半徑為0.5 m、彎管角度為90°的彎管上激勵(lì)T(0,1)模態(tài)導(dǎo)波。對(duì)比激勵(lì)頻率為50 kHz和150 kHz兩個(gè)模型，導(dǎo)波在彎管上傳播的形態(tài)和所提取的T(0,1)模態(tài)導(dǎo)波信號(hào)，如圖4所示。

從圖4(a)和4(b)可以看出：激勵(lì)頻率為150 kHz相較于50 kHz，彎管中有新波前產(chǎn)生，新波前從彎管內(nèi)側(cè)向外側(cè)擴(kuò)展。將接收位置A-A處的12個(gè)點(diǎn)所收到的時(shí)域波形以周向分布形式畫出，如圖4(c)和4(d)所示。其中，橫軸代表時(shí)間，縱軸代表角度位置，圖中顏色代表位移幅度。對(duì)比圖4(c)和4(d) 可知：激勵(lì)頻率為50 kHz時(shí)比150 kHz時(shí)的T(0,1)導(dǎo)波脈沖寬度大，各點(diǎn)信號(hào)嚴(yán)重不均衡。50 kHz時(shí)，由于低頻導(dǎo)波有更大的波長(zhǎng)，所以相同的周期數(shù)下脈沖更寬，那么新產(chǎn)生的波前和原波前未能分離開，導(dǎo)致兩者相互疊加形成干涉，引起透過(guò)率的降低；而150 kHz時(shí)，由于導(dǎo)波脈沖較窄，新形成的波前和原波陣面清晰可辨，所以干涉效果較弱。因此，150 kHz時(shí)的透過(guò)率會(huì)大于50 kHz時(shí)的透過(guò)率，如圖4(e)和4(f)所示。在圖4(a)～4(d)中，兩種頻率下的導(dǎo)波能量分布和集中程度也不一致，但能量都在彎管外側(cè)集中較強(qiáng)。

(a) 激勵(lì)頻率為50 kHz，波動(dòng)位移分布圖

(b) 激勵(lì)頻率為150 kHz，波動(dòng)位移分布圖

(c) 激勵(lì)頻率為50 kHz，接收位置A-A上12個(gè)點(diǎn)的信號(hào)周向分布圖

(d) 激勵(lì)頻率為150 kHz，接收位置A-A上12個(gè)點(diǎn)的信號(hào)周向分布圖

(e) 激勵(lì)頻率為50 kHz，T(0,1)導(dǎo)波信號(hào)

(f) 激勵(lì)頻率為150 kHz，T(0,1)導(dǎo)波信號(hào)

圖4 激勵(lì)頻率分別為50 kHz和150 kHz時(shí)：(a)與(b)是某時(shí)刻導(dǎo)波在彎管上的波動(dòng)位移分布圖；(c)與(d)是過(guò)彎管接收位置A-A上12個(gè)點(diǎn)的信號(hào)周向分布圖；(e)與(f)是由12個(gè)接收信號(hào)相加所提取的T(0,1)導(dǎo)波信號(hào)

Fig.4 When the excitation frequencies are respectively 50 kHz and 150 kHz, the displacement contours of the bend are shown in (a) and (b); the displacements at 12 evenly circumferential points are shown in (c) and (d); and the signals of T(0,1) mode after adding the 12 received signals are shown in (e) and (f)

1.3 彎曲半徑和透過(guò)率的關(guān)系

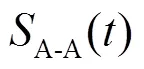
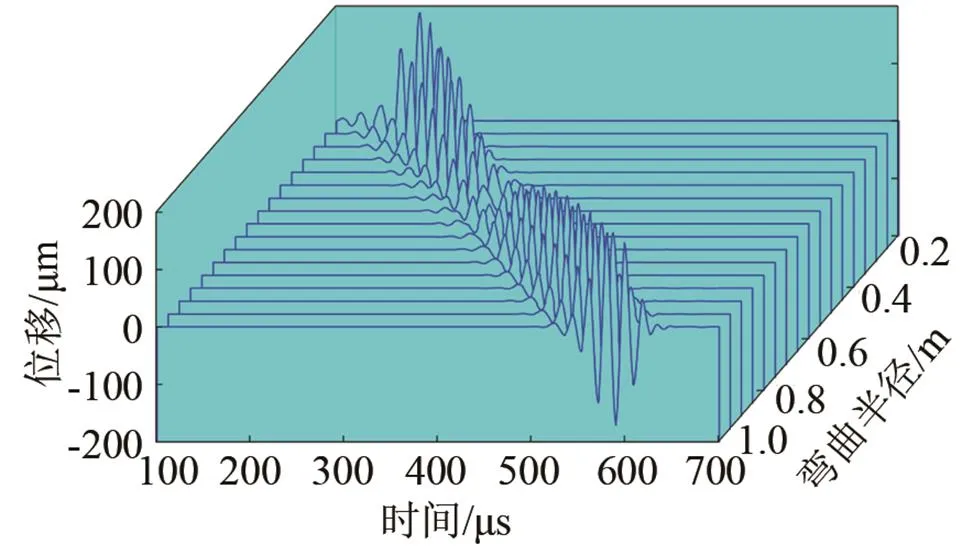
(a) 時(shí)域信號(hào)

(b) 透過(guò)率隨彎曲半徑的變化曲線

圖5 在彎曲角度為90°時(shí)，不同彎曲半徑彎管上的接收信號(hào)及透過(guò)率

Fig.5 (a)- the received signals of T(0,1) mode after propagating across the bends of 90° bend angle with different bend radii and (b)- the transmission coefficients vs. the bend radius

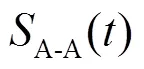
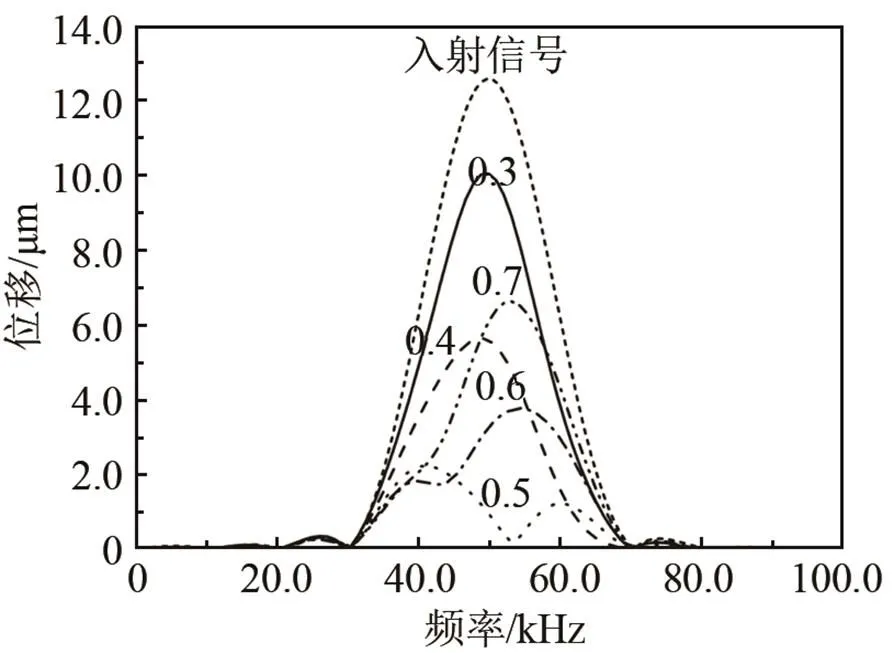
圖6 經(jīng)過(guò)不同彎曲半徑的彎管后，T(0,1)模態(tài)導(dǎo)波的頻域信號(hào)

從圖7可知：激勵(lì)頻率50 kHz的T(0,1)模態(tài)導(dǎo)波分別經(jīng)過(guò)彎曲半徑0.5 m和1.0 m的彎管后，接收端的12個(gè)信號(hào)不僅在幅度上而且在相位上也存在差別。當(dāng)12個(gè)信號(hào)相加提取T(0,1)模態(tài)導(dǎo)波時(shí)，由于導(dǎo)波經(jīng)過(guò)彎曲半徑0.5 m的彎管后的12個(gè)信號(hào)相位相差大(如圖7(a))，所以形成相減干涉，導(dǎo)致透過(guò)率降低；而導(dǎo)波經(jīng)過(guò)彎曲半徑1.0 m的彎管后的12個(gè)信號(hào)相位相近(如圖7(c))，所以透過(guò)率降低較小。

1.4 彎管角度和透過(guò)率的關(guān)系

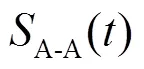
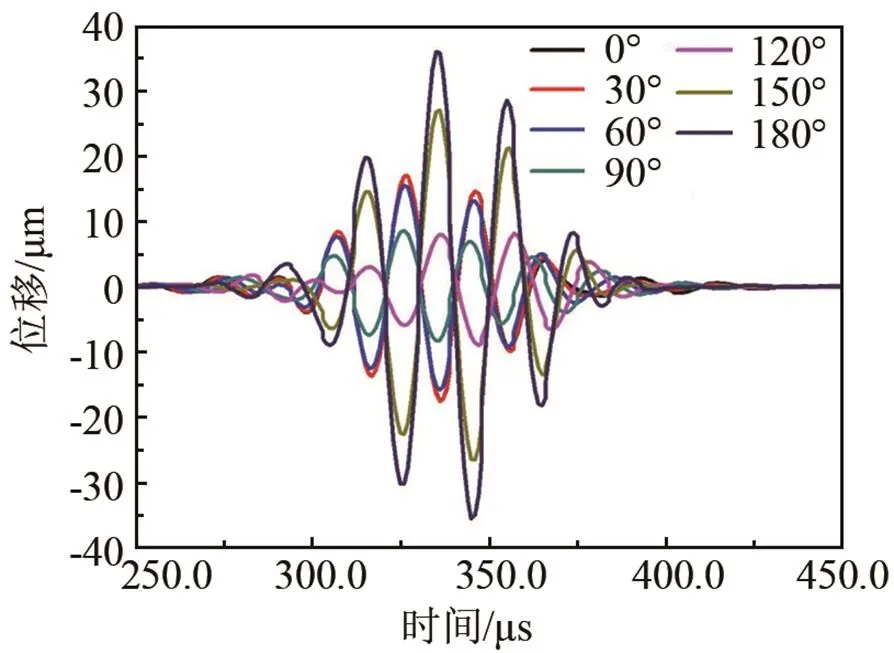
(a) 彎曲半徑為0.5 m時(shí)，接收端7點(diǎn)接收的時(shí)域信號(hào)

(b) 彎曲半徑為0.5 m時(shí)，導(dǎo)波T(0,1)信號(hào)

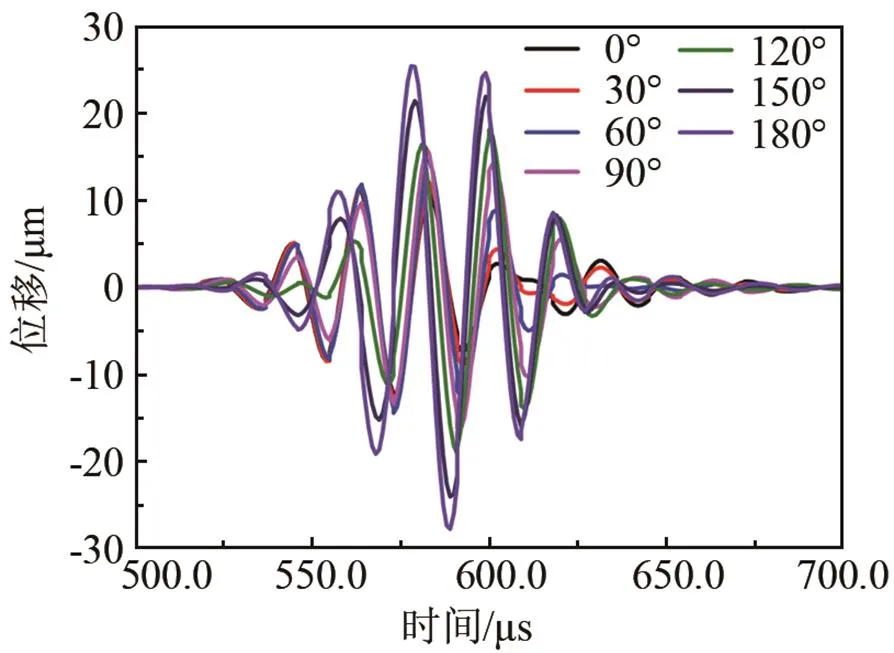
(c) 彎曲半徑為1.0 m時(shí)，接收端7點(diǎn)接收的時(shí)域信號(hào)

(d) 彎曲半徑為1.0 m時(shí)，導(dǎo)波T(0,1)信號(hào)

圖7 彎管彎曲半徑為0.5 m和1.0 m時(shí)，A-A接收端7點(diǎn)接收的時(shí)域信號(hào)分別為(a)、(c)；A-A接收端12個(gè)信號(hào)相加后提取的T(0,1)導(dǎo)波信號(hào)分別為(b)、(d)

Fig.7 When the bend radius are respectively 0.5 m and 1.0 m, the seven signals received at the seven points of the A-A monitoring end are shown in (a) and (c) and the signal of T(0,1) mode from adding 12 signals received respectively at the 12 points of the A-A monitoring end are shown in (b) and (d)

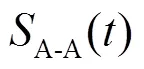
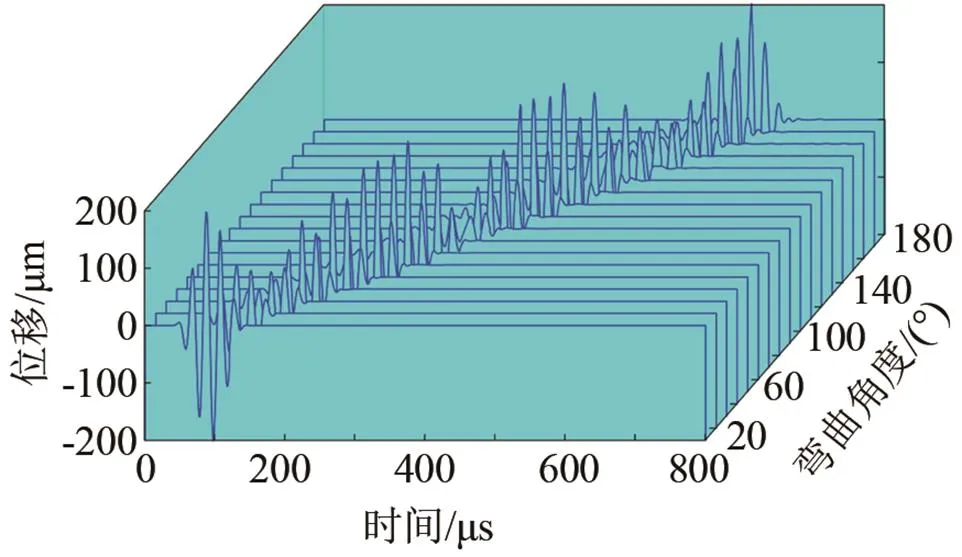
(a) T(0,1)模態(tài)態(tài)導(dǎo)波的時(shí)域信號(hào)

(b) 透過(guò)率隨彎曲角度的變化曲線

圖8 在彎曲半徑0.5 m的不同彎曲角度的彎管上接收的信號(hào)及透過(guò)率

Fig.8 (a)- the received signals of T(0,1) mode after propagating across the bends of 0.5 m bend radius with different bend angles and (b)- the transmission coefficient vs. the bend angle

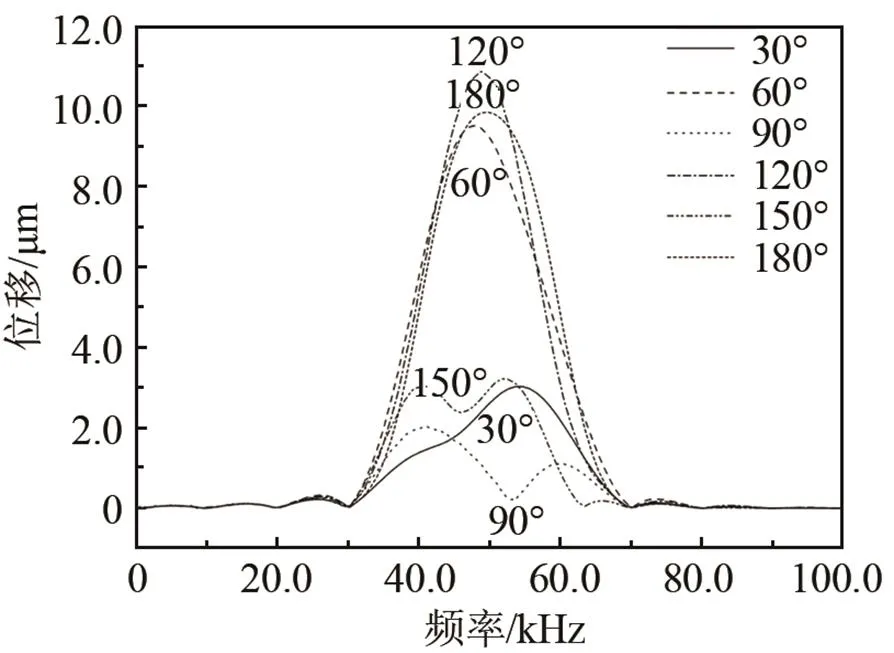
圖9 經(jīng)過(guò)不同角度的彎管，T(0,1)模態(tài)導(dǎo)波的頻譜曲線

由圖9可知：在彎曲角度為30°、90°和150°的彎管上都發(fā)生了相減干涉，并且90°和150°彎管上的頻譜曲線都出現(xiàn)了波谷，且最小值出現(xiàn)在不同的頻率上。

2 實(shí)驗(yàn)

2.1 實(shí)驗(yàn)材料及方法

實(shí)驗(yàn)用彎管的規(guī)格：外徑108 mm，壁厚8 mm。彎管角度90°，彎曲半徑0.7 m，管子的材料為45#鋼。采用自制導(dǎo)波檢測(cè)儀和探頭環(huán)，探頭環(huán)由周向均勻分布的12個(gè)橫向切變模的壓電探頭組成，并可通過(guò)機(jī)械裝置裝卡在管子外壁上。探頭使管外壁周向振動(dòng)，激勵(lì)T(0,1)模態(tài)導(dǎo)波。導(dǎo)波激勵(lì)信號(hào)為加漢寧窗的5周期正弦函數(shù)信號(hào)。在彎管的兩端分別布置探頭環(huán)A和探頭環(huán)B，如圖10所示。探頭環(huán)B激勵(lì)T(0,1)導(dǎo)波，導(dǎo)波經(jīng)過(guò)彎管后被探頭環(huán)A接收，其接收信號(hào)的峰峰值記為I；然后，將探頭環(huán)B裝卡在距離探頭環(huán)A相同距離1.1 m(彎管段的長(zhǎng)度)的直管段上，探頭環(huán)A接收信號(hào)的峰峰值記為II。那么，T(0,1)導(dǎo)波經(jīng)過(guò)彎管后的透過(guò)率=I/II。

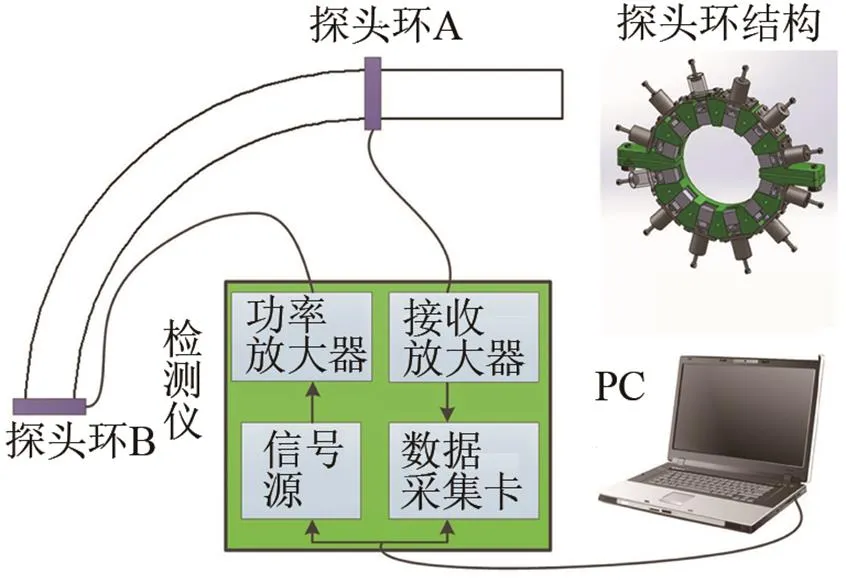
圖10 檢測(cè)裝置示意圖

2.2 實(shí)驗(yàn)結(jié)果

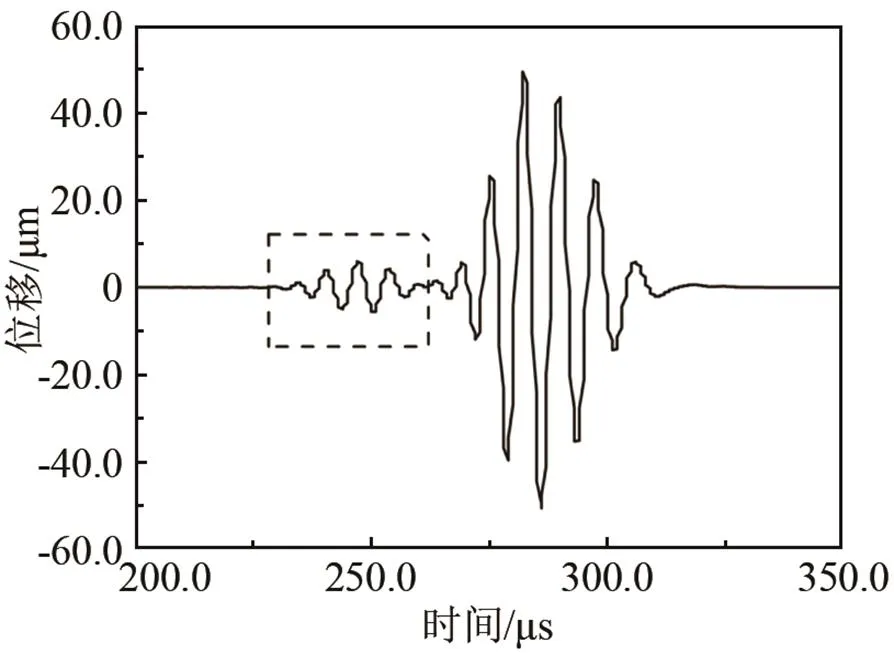
改變探頭的激勵(lì)頻率從25 kHz到85 kHz，以5 kHz的間隔變化。其中，激勵(lì)頻率為30 kHz的T(0,1)模態(tài)導(dǎo)波信號(hào)如圖11(a)所示，從時(shí)域信號(hào)中計(jì)算得到T(0,1)模態(tài)導(dǎo)波的群速度為3 323 m/s，與理論計(jì)算得到的群速度相差不大，由此可說(shuō)明管中的導(dǎo)波為T(0,1)模態(tài)。對(duì)導(dǎo)波信號(hào)進(jìn)行傅里葉變換，得到如圖11(b)中的信號(hào)頻譜圖。從圖11(b)中可以看出，導(dǎo)波信號(hào)的中心頻率大致為30 kHz，說(shuō)明探頭的性能良好。得到不同激勵(lì)頻率下透過(guò)率和激勵(lì)頻率的關(guān)系，如圖12所示。

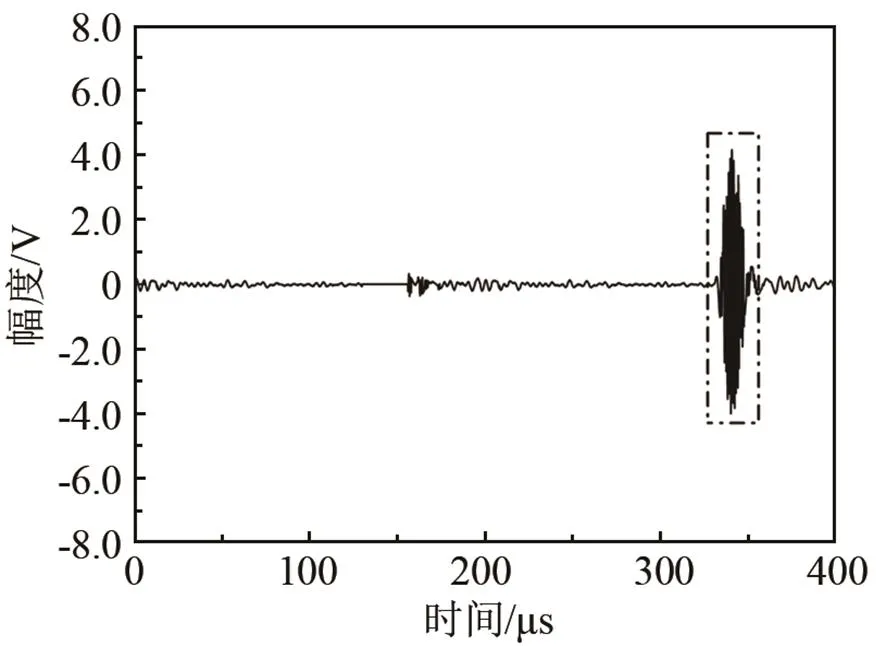
(a) 時(shí)域信號(hào)

(b) 頻域信號(hào)

圖11 探頭環(huán)A接收到的探頭環(huán)B激勵(lì)的30 kHz的T(0,1)模態(tài)信號(hào)

Fig.11 (a)- the signal of T(0,1) mode activated by ring B and (b)- the signal received by ring A

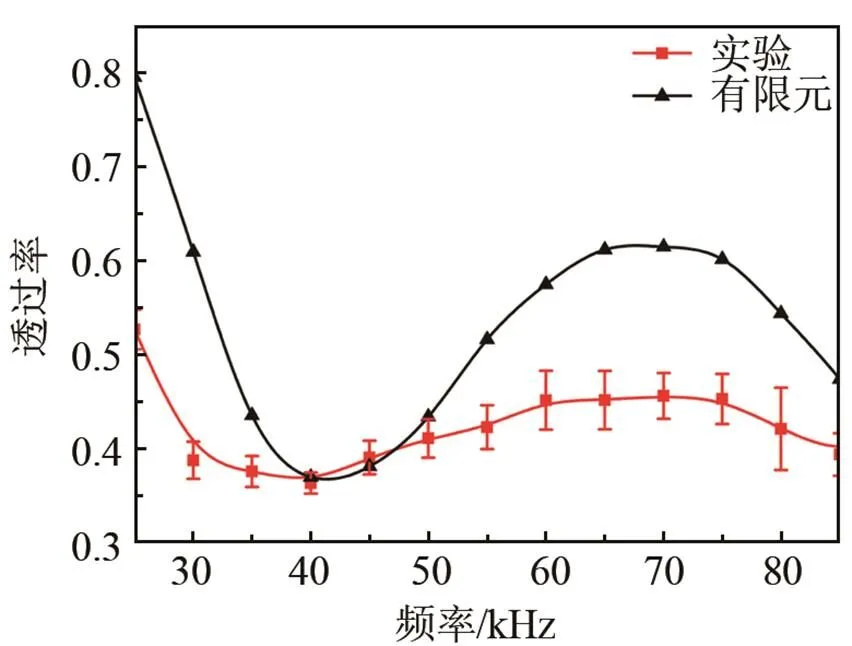
圖12 不同激勵(lì)頻率下的透過(guò)率

從圖12中可知：實(shí)驗(yàn)結(jié)果和有限元模擬結(jié)果有一定的誤差，但是在整體的變化趨勢(shì)上是一致的。誤差來(lái)源的可能原因：其一，由于探頭環(huán)需要兩次機(jī)械裝卡，無(wú)法保證裝卡的一致性；其二，探頭環(huán)上的12個(gè)探頭無(wú)法保證其性能完全均勻一致。因此，在提取T(0,1)模態(tài)導(dǎo)波時(shí)，實(shí)驗(yàn)結(jié)果不能得到有限元模擬的理想結(jié)果。在實(shí)際檢測(cè)中，頻率選擇不當(dāng)就會(huì)造成透過(guò)率很小，如實(shí)驗(yàn)中40 kHz時(shí)的情況。

3 結(jié)論

T(0,1)模態(tài)導(dǎo)波在經(jīng)過(guò)彎管時(shí)，由于探頭環(huán)安裝在管子的某個(gè)截面上，導(dǎo)波在彎管上傳播到達(dá)探頭環(huán)的各個(gè)探頭的時(shí)間就不同，使探頭環(huán)的各通道接收的信號(hào)產(chǎn)生相位差異，不同的激勵(lì)頻率產(chǎn)生不同的相位差，從而形成了不同程度的干涉，造成彎管透過(guò)率的變化。

由于彎管參數(shù)不同，導(dǎo)致各個(gè)通道接收信號(hào)的相位差變化。因此，T(0,1)模態(tài)導(dǎo)波在不同彎曲半徑、彎曲角度的彎管上傳播時(shí)，形成不同程度的干涉，導(dǎo)致透過(guò)率變化。

激勵(lì)頻率為50 kHz的T(0,1)模態(tài)導(dǎo)波，在彎曲角度為90°的彎管上，其透過(guò)率隨彎管角度呈周期性變化。

為了避免相減干涉的發(fā)生，提高信號(hào)的透過(guò)率，應(yīng)采用多個(gè)頻率來(lái)檢測(cè)有彎管段的管道。

[1] Gazis D C. 3-Dimensional investigation of the propagation of waves in hollow circular cylinder. 1. analytical foundation[J]. J. Acoust. Soc. Am., 1959, 31(5): 568-573.

[2] Gazis D C. 3-Dimensional investigation of the propagation of waves in hollow circular cylinders. 2. numerical results[J]. J. Acoust. Soc. Am., 1959, 31(5): 573-578.

[3] Hayashi T, Kawashima K, Sun Z Q, et al. Guided wave propagation mechanics across a pipe elbow[J]. J. Pressure Vessel Technol., 2005, 127(3): 322-327.

[4] Demma A, Cawley P, Lowe M, et al. The effect of bends on the propagation of guided waves in pipes[J]. J. Pressure Vessel Technol., 2005, 127(3): 328-335.

[5] Sanderson R M, Hutchins D A, Billson D R, et al. The investigation of guided wave propagation around a pipe bend using an analytical modeling approach[J]. J. Acoust. Soc. Am., 2013, 133(3): 1404-1414.

[6] Nishino H, Yoshida K, Cho H, et al. Propagation phenomena of wideband guided waves in a bended pipe[J]. Ultrasonics, 2006, 44: 1139-1143.

[7] 周紹萍, 張蒲根, 呂文超, 等. 基于導(dǎo)波的彎管裂紋缺陷的檢測(cè)[J]. 機(jī)械工程學(xué)報(bào), 2015, 51(6): 58-65. ZHOU Shaoping, ZHANG Pugen, Lü Wenchao, et al. Detection of cracks in elbow pipes using guided waves[J]. Journal Of Mechanical Engineering, 2015, 51(6): 58-65.

[8] 鄧菲, 陳洪磊, 張僖. 基于寬頻激勵(lì)的管型結(jié)構(gòu)導(dǎo)波檢測(cè)[J]. 機(jī)械工程學(xué)報(bào), 2014, 50(18): 23-28. DENG Fei, CHEN Honglei, ZHANG Xi. Pipe structure detection based on broadband guided wave excitation[J]. Journal of Mechanical Engineering, 2014, 50(18): 23-28.

[9] 王悅民, 宗侶, 朱龍翔, 等. 多彎頭管道磁致伸縮導(dǎo)波無(wú)損檢測(cè)技術(shù)[J]. 海軍工程大學(xué)學(xué)報(bào), 2015, 27(2): 42-45. WANG Yuemin, ZONG Lü, ZHU Longxiang, et al. Guided wave non-destructive testing technology of multi-elbow pipe based on magnetostrictive effect[J]. Journal of Naval University of Engineering, 2015, 27(2): 42-45.

[10] Alleyne D N, Pavlakovic B, Lowe M J S, et al. Rapid long-range inspection of chemical plant pipework using guided waves[J]. Insight, 2001, 43(2): 93-98.

[11] 趙繼辰, 吳斌, 何存富. 螺旋波紋管導(dǎo)波檢測(cè)技術(shù)的數(shù)值仿真和試驗(yàn)研究[J]. 機(jī)械工程學(xué)報(bào), 2012, 48(24): 8-13. ZHAO Jichen, WU Bin, HE Cunfu. Numerical simulation and experimental research on helical bellows by using guided wave technology[J]. Journal of Mechanical Engineering, 2012, 48(24): 8-13.

[12] 程載斌, 王志華, 張立軍, 等. 管道超聲縱向?qū)Р鸭y檢測(cè)數(shù)值模擬[J]. 應(yīng)用力學(xué)學(xué)報(bào), 2004, 21(4): 76-80. CHENG Zaibin, WANG Zhihua, ZHANG Lijun, et al. Ma hongwei. numerical simulation of crack detection in pipes using ultrasonic longitudinal guided wave[J]. Chinese Journal of Applied Mechanics, 2004, 21(4): 76-80.

[13] Brath A J, Simonetti F, Nagy P B, et al. Guided wave radiation from a point source in the proximity of a pipe bend[J]. 40th Annual Review of Progress in Quantitative Nondestructive Evaluation: Incorporating the 10th International Conference on Barkhausen Noise and Micromagnetic Testing, 2014, 33a& 33b(1581): 316- 323.

[14] QI Minxin, ZHOU Shaoping, NI Jing, et al. Investigation on ultrasonic guided waves propagation in elbow pipe[J]. International Journal of Pressure Vessels and Piping, 2016, 139-140:250-255.

Numerical and experimental research on T(0,1) guided waves propagating in bended pipes

LI Yang1, ZOU Yun1, ZHANG Shuang-nan2, CAI Gui-xi2

(1. School of Mechanical Engineering, Zhengzhou University, Zhengzhou 450001,He’nan, China;2. Institute of Metal Research, Chinese Academy of Sciences, Shenyang 110016,Liaoning, China)

Propagation of guided waves in bended pipes is more complicated than that in straight pipes because of the complex geometry of bends. The transmission coefficient is an important factor used to evaluate the accuracy of the test. In this study, the finite-element method (FEM) is used to investigate the influences of the angle of bends, the radius of bends and the excitation frequencies on the transmission coefficients of T(0,1) guided waves. Our results show that the transmission coefficients varied with the excitation frequencies of guided waves when propagating through a bend. Given that the frequency of guided wave is high enough, new wave fronts are more easily produced after the guided wave propagating through a bend. It is also found that when guided waves propagating through a bend with the minimal transmission coefficient, their frequencies are correlated with the angle and the radius of the bend. The transmission coefficients oscillate periodically with increasing angle of the bend. The correlation between transmission coefficients and frequencies of the guided waves is verified by experimental data. In conclusion, it is suggested that guided waves propagating at various frequencies should be used to test bended pipes.

transmission coefficients; bended pipes; T(0,1) mode; propagation characteristic

TB559

A

1000-3630(2017)-05-0442-08

10.16300/j.cnki.1000-3630.2017.05.008

2016-09-13;

2016-12-30

河南省教育廳高等學(xué)校重點(diǎn)科研項(xiàng)目(18A460032)

李陽(yáng)(1988－), 男, 河南焦作人, 博士, 講師, 研究方向?yàn)槌晫?dǎo)波的工程化應(yīng)用。

李陽(yáng), E-mail: yangli@zzu.edu.cn