一種新的抗滑樁加固邊坡穩定的計算方法

孫 博

(中國電建集團成都勘測設計研究院有限公司， 四川 成都 610072)

一種新的抗滑樁加固邊坡穩定的計算方法

孫 博

(中國電建集團成都勘測設計研究院有限公司， 四川 成都 610072)

以抗滑樁的設計理論為基礎，結合Rocscience Slide軟件(或Slope/W軟件)和理正軟件，提出一種新的抗滑樁加固邊坡穩定的計算方法。該方法采用剛體極限平衡法計算邊坡的穩定性，彈性計算方法計算抗滑樁的內力和位移，并將邊坡穩定計算和抗滑樁內力計算有機的結合起來，避免了傳統設計方法中兩部分內容的相互脫節。同時，該方法避免了傳統設計方法的復雜性和繁瑣性，可以考慮多種荷載的影響，提高了設計效率和設計準確性。

抗滑樁；邊坡；穩定；剛體極限平衡法；設計

0 前 言

抗滑樁是一種廣泛應用的加固邊坡的方法，特別適用于土質邊坡或堆積體邊坡。與其他處理措施(如削坡、格構錨索、擋土墻等)相比，抗滑樁對坡體的擾動較小、受雨水或庫水弱化的影響較小、耐久性及經濟性較好。因此，在處理深厚覆蓋層邊坡或堆積體邊坡時，抗滑樁處理措施成為設計工程師的首選。

抗滑樁的受力非常復雜，包括作用在樁后的橫向滑坡推力(有地下水時，應計入孔隙水壓力)和樁前土體抗力(由樁前土體剩余抗滑力、被動土壓力或彈性抗力中小者決定)。目前，國內抗滑樁的計算方法主要有懸臂樁法[1]、地基系數法[1-4]和數值方法[5-7]等。相對來說，數值方法可以真實的考慮樁、土之間的相互作用，計算精度相對較高。但是，數值方法計算過程比較復雜，且耗時較長，對設計人員來說在工程前期階段采用數值方法進行抗滑樁的設計是不太現實的，故目前設計人員采用的主要是地基系數法。采用地基系數法，有兩個問題比較難以解決：一是滑動面的確定；二是作用于樁上的滑坡推力和樁前滑體抗力，并且兩個問題相互影響。一般來說，邊坡滑動面的確定是采用二維剛體極限平衡法，且該方法比較成熟，有專業的商業軟件，如Rocscience slide[8]、Slope/W[9]等。而對于樁上滑坡推力和樁前滑體抗力，國內一般是采用傳遞系數法[10]，而傳遞系數法需要假定滑動面為折線形，計算過程異常復雜，且考慮孔隙水壓力和庫水壓力時計算量劇增。鑒于此，計算滑坡推力時大都假定折線形滑面，且對荷載進行一定的簡化。

傳統設計方法在處理邊坡穩定和抗滑樁設計時，一般是采用剛體極限平衡法確定邊坡滑動面；然后采用傳遞系數法計算抗滑樁的滑體抗力和滑坡推力；最后采用地基系數法計算抗滑樁的內力和位移，并進行配筋設計。大多情況下，傳統設計方法不會再進行邊坡穩定的復核。當滑動面比較明確(如軟弱結構面、斷層等)時，傳統設計方法不會有問題。但當滑動面不唯一時，有可能出現新的失穩滑動面(如從樁頂剪出)。鑒于傳統設計方法的復雜性和不可靠性，本文結合Rocscience Slide軟件(或Slope/W軟件)和理正軟件，提出一種新的抗滑樁加固邊坡的設計方法，以提高設計效率和設計準確性。

1 計算方法簡介

抗滑樁的設計涉及兩方面的內容：一是邊坡的穩定，二是抗滑樁自身設計。其中邊坡穩定分析包括天然(未加固)邊坡的穩定狀況和加固后的穩定狀況，而抗滑樁自身設計包括樁截面、長度、樁間距和配筋設計等。本文提出的計算方法綜合考慮了這兩方面因素，并通過Rocscience Slide軟件(或Slope/W軟件)與理正軟件將兩者有機的結合起來。該方法主要計算流程見圖1。

(1)天然邊坡的穩定性分析。基于Rocscience Slide軟件(或Slope/W軟件)，采用剛體極限平衡法計算未加固邊坡的穩定性，確定最可能失穩滑動面。

(2)抗滑樁的初步設計。根據天然邊坡的穩定性，并類比相關工程，初步確定抗滑樁的截面尺寸、樁長、樁間距和布置位置，其中布置位置可根據最可能失穩滑動面初步確定，無嚴格要求。

圖1 計算流程示意

在Rocscience Slide軟件(或Slope/W軟件)中，分析樁的抗滑作用，只需輸入樁的間距、抗剪力大小及其方向三個關鍵參數即可。三個參數中，樁間距是明確的，而抗剪力大小及其方向是令人困惑的。眾所周知，抗滑樁斜截面是可以承擔剪力的，故抗剪力方向可以認為平行于滑動面。一般來說，抗滑樁是不布置彎起鋼筋的，其斜截面承載力主要由混凝土和箍筋決定，故其抗剪力大小可按式(1)計算[11]：

(1)

式中V——抗滑樁斜截面抗剪力設計值；

Vc——混凝土的受剪承載力；

Vsv——箍筋的受剪承載力；

Asv——配置在同一截面內箍筋各肢的全部截面面積；

ft——混凝土軸心抗拉強度設計值；

fyv——箍筋抗拉強度設計值；

γd——結構系數；

b——抗滑樁截面寬度；

h0——抗滑樁截面有效高度；

s——沿構件長度方向上箍筋的間距。

(3)抗滑樁加固后邊坡穩定性驗算。采用Rocscience Slide軟件(或Slope/W軟件)計算抗滑樁加固后的邊坡穩定性。如果邊坡安全系數不滿足規范要求，則根據滑坡體與抗滑樁的位置關系(見圖2)，按下文調整相關參數。

圖2 滑坡體與抗滑樁位置關系

①圖(a)所示：滑動面剪出口位于抗滑樁上部邊坡，這表明抗滑樁位置偏低，需向上布置。

②圖(b)所示：滑動面剪出口位于抗滑樁以下邊坡，且滑動面從抗滑樁底部穿過，這表明抗滑樁樁長不夠，需增加樁的長度。

③圖(c)所示：滑動面剪出口位于抗滑樁下部邊坡，且滑動面穿過抗滑樁，這表明抗滑樁抗剪力不夠，需增加抗滑樁抗剪力。對于抗滑樁來說，增加其抗剪力主要有兩種方式，一是增加箍筋面積；二是增大樁的截面尺寸。計算時一般先調整箍筋面積，如仍不滿足，則再考慮調整樁的截面尺寸。

不斷調整抗滑樁的相關設計參數并進行邊坡穩定驗算，直到邊坡穩定安全系數達到或稍大于規范允許值為止。需要注意的是，在調整抗滑樁的相關參數時，各參數每次調整量不宜過大，以避免抗滑樁設計過于保守。

(4)抗滑樁設計復核。基于理正軟件中抗滑樁設計模塊，分析抗滑樁受力、樁體位移及其配筋面積。在計算過程中，樁前滑體抗力和樁上滑坡推力是兩個關系參數。在以往計算中，這兩個參數大都是通過傳遞系數法來計算的，計算過程復雜、繁瑣。而在該計算方法中，兩個荷載分別為步驟(1)和(3)中樁后的條塊受到樁前條塊給予的條間力，一般取水平力即可。需注意兩個荷載對應的條塊是相同的，即兩個步驟中的滑動面是一致的。

(5)校核。對比分析步驟(2)、(3)和(4)，確保兩個軟件中有關抗滑樁的設計參數一致，且抗滑樁加固后邊坡穩定。同時，根據步驟(4)的相關成果，并結合工程經驗，合理配置抗滑樁鋼筋。

2 新方法的特點

與傳統的抗滑樁加固邊坡的設計方法相比，新方法具有以下特點：

(1)新方法將邊坡穩定計算與抗滑樁復核計算有機的結合到一起，避免了傳統設計方法中兩部分計算內容的相互脫節以及由此導致的計算錯誤。

(2)新方法容易獲得樁前滑體抗力和樁上滑坡推力，且兩個荷載的計算方法與邊坡穩定計算方法是一致的，均是通過折減巖土體強度參數(c,φ)達到極限平衡狀態得到的，避免了傳遞系數法的復雜性、繁瑣性、不一致性(與邊坡穩定計算方法)和不準確性(荷載的簡化、滑動面的簡化等)。

(3)新方法能夠考慮多種荷載(如孔隙水壓力、庫水壓力、地震力等)對邊坡穩定的影響，而傳統方法對荷載一般采取一定的簡化以避免計算的繁瑣性和復雜性。

(4)新方法能夠解決復雜地質條件的邊坡失穩與加固問題，而傳統方法會對地質條件進行一定的簡化。

(5)新方法可以采用多種計算方法(如Bishop法、Janbu法等)和多種失穩模式(如圓弧形、折線形等)計算邊坡的穩定性，而傳統設計方法計算邊坡穩定性的方法和形式比較單一。

3 驗證分析

本節以抗滑樁加固某簡單邊坡為例，詳細介紹本文提出的抗滑樁加固邊坡穩定的計算方法，其中邊坡穩定計算采用Rocscience Slide軟件，抗滑樁設計采用理正軟件。

3.1 計算模型及計算參數

以文獻[12]中的簡單均質邊坡為例，計算模型幾何尺寸見圖3。邊坡土體參數：容重γ=20 kN/m3，φ′=40°，c′=12 kPa，ru=0.5。

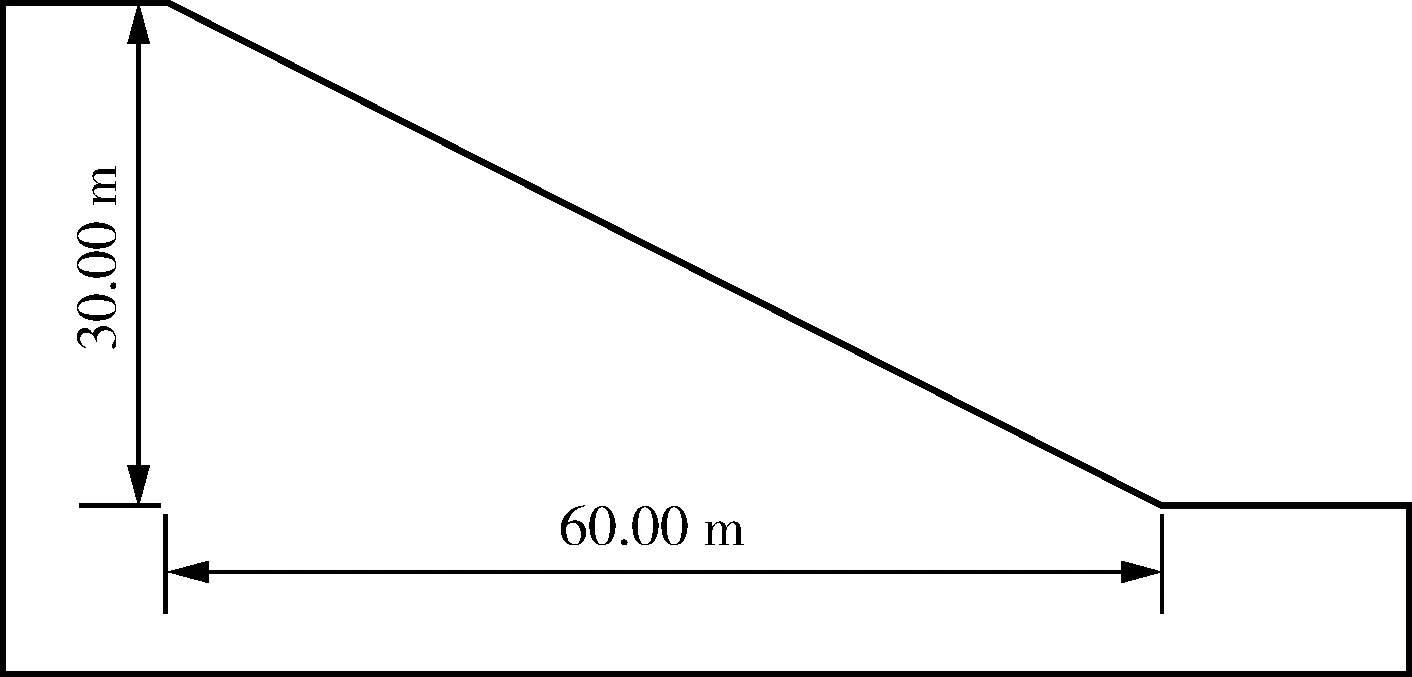
圖3 計算模型

3.2 計算分析

(1)未加固邊坡的穩定性分析。基于Rocscience Slide軟件，假定為圓弧滑動，采用Spencer法得到邊坡的安全系數為1.02，與文獻[12]的結果相同，最小滑動面見圖4。假定該邊坡設計安全系數為1.10，下面將采用抗滑樁對其進行加固處理。

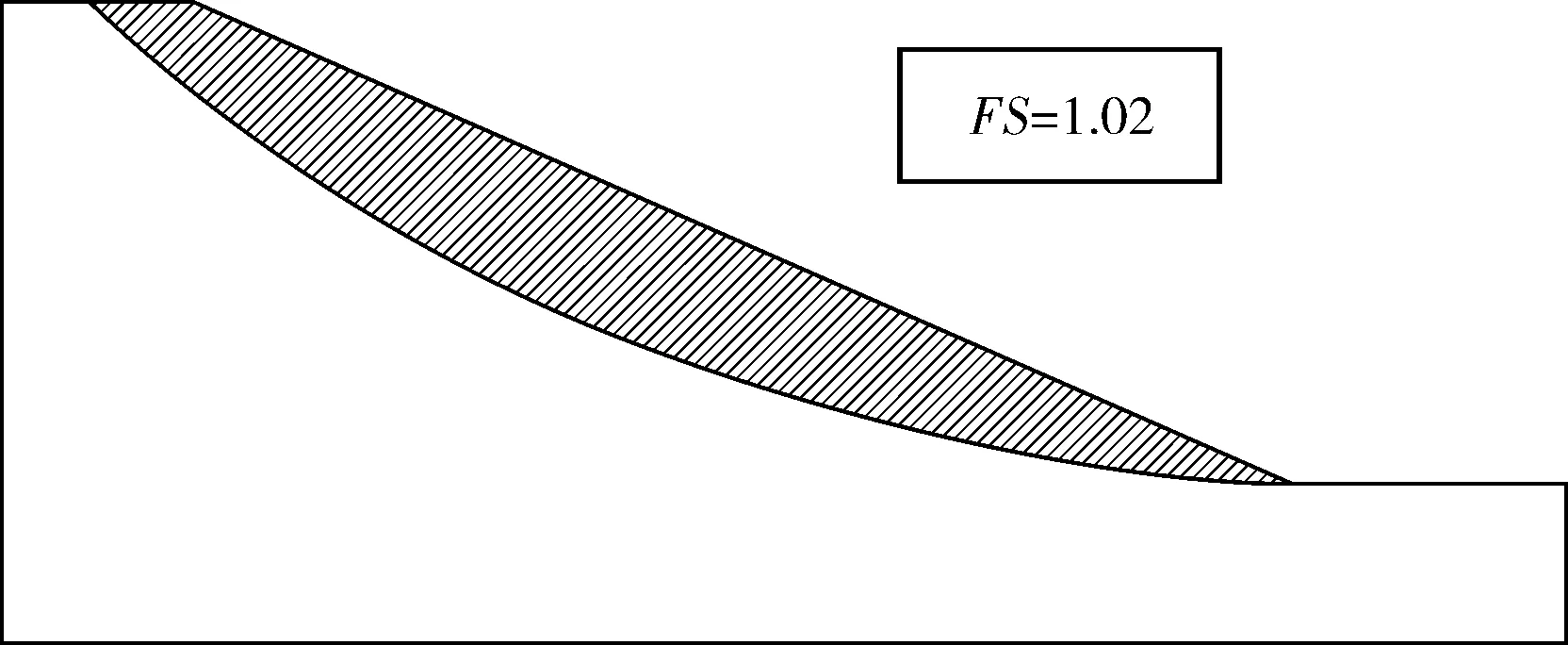
圖4 邊坡最小安全系數滑弧面

(2)抗滑樁初步設計。根據邊坡穩定計算成果，并類比相關工程，初步設計抗滑樁截面尺寸為1.5 m×2.0 m，長15 m，樁間中心距為6 m，箍筋φ16 mm@20 cm。由式(1)可得抗滑樁的設計抗剪力為3 570 kN，取為3 500 kN。由于滑動面剪出口位于坡腳，故抗滑樁初步布置在距坡腳6 m高度處。

(3)抗滑樁加固后邊坡穩定性。根據抗滑樁的初步設計參數，基于Rocscience Slide軟件，校核加固后的邊坡穩定性。由計算可知安全系數為1.08，且剪出口位于抗滑樁上部邊坡，這表明抗滑樁布置過低，需上移抗滑樁。經反復試算后，當抗滑樁距坡腳高度為8 m時，邊坡穩定安全系數為1.105，稍大于設計值，這表明抗滑樁的主要設計參數是合理的。

(4)抗滑樁設計復核。基于理正軟件，根據前面三步的計算和設計成果，輸入相關參數。其中嵌入段長度等于樁長與相應位置處最可能失穩滑動面(步驟(1))高度之差；推力分布類型假定為矩形，且滑體抗力等于步驟(1)中靠近抗滑樁位置的左側條塊右側水平力，而樁上滑坡推力等于步驟(3)中靠近抗滑樁位置的左側條塊右側水平力。由于該邊坡為土質邊坡，故樁底支承條件為自由；且土反力計算系數采用“m”法，按文獻[10]，m取為1 000 kPa/m2。其余有關邊坡的幾何參數、土體物理力學參數和抗滑樁設計參數與前面參數一致。

經計算可知，樁身擋土側承受的最大彎矩為9 195.47 kN·m，距樁頂8 m；最大剪力為2 293.73 kN，距樁頂5.87 m(抗滑樁錨固點)；樁的最大位移為154 mm；擋土側縱筋面積為7 065 mm2，非擋土側縱筋面積為6 000 mm2，箍筋面積為377 mm2。抗滑樁內力和位移見圖5。

(5)校核。根據前面幾步的計算成果，校核抗滑樁的相關設計參數，確定抗滑樁的截面尺寸為1.5 m×2.0 m，樁長15 m，樁間中心距為6 m，樁距坡腳高度為8 m，同時根據步驟(4)的計算成果，抗滑樁擋土側配置12根φ28 mm鋼筋，非擋土側配置10根φ28 mm鋼筋，左右兩側配置合理的構造鋼筋，箍筋為φ16 mm@20 cm。

4 結 論

鑒于傳統抗滑樁加固邊坡穩定的計算方法的復雜性、繁瑣性和不可靠性，本文提出了一種新的計算方法。該方法采用剛體極限平衡法計算邊坡穩定，彈性計算方法計算抗滑樁的內力和位移，并通過Rocscience Slide軟件(或Slope/W軟件)和理正軟件將兩部分內容有機的結合起來。同時，以抗滑樁加

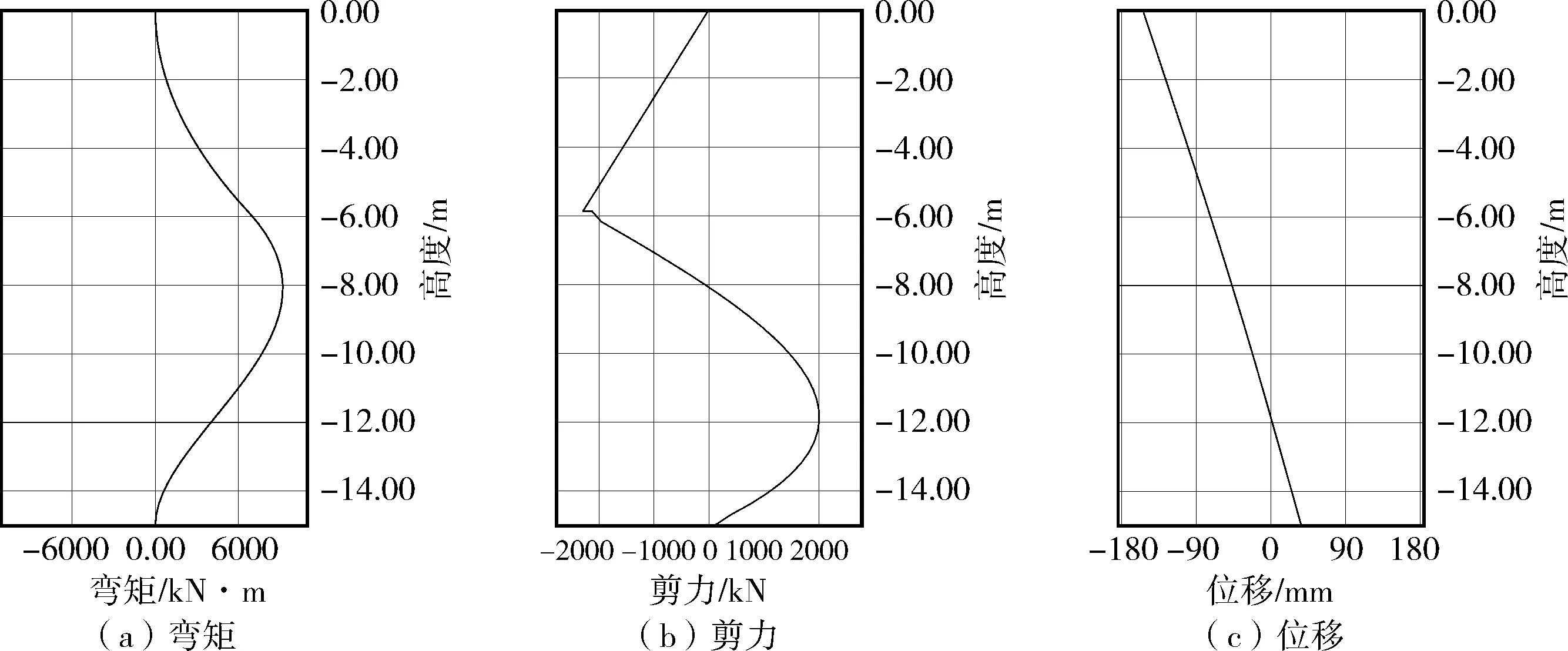
圖5 抗滑樁內力和位移示意

固簡單邊坡為例，證明了該方法的實用性。該方法的推廣應用，可大大提高設計效率和設計準確性。

[1] 鐵道部第二勘測設計院. 抗滑樁設計與計算[M]. 北京：中國鐵道出版社，1983.

[2] 胡煥校，劉靜，吳海濤. 基于綜合剛度雙參數法抗滑樁的數值分析[J]. 礦冶工程, 2009,29(3)：11-15.

[3] 戴自航，蘇美選，胡昌斌. 拋物線分布荷載推力樁雙參數法的2種數值解[J]. 巖石力學與工程學報，2007,26(7)：1463-1469.

[4] 鄒盛堂，戴自航. 抗滑樁計算的綜合剛度與三參數法數值解[J]. 巖石力學與工程學報, 2014,33(增2)：3718-3723.

[5] 戴自航，徐祥. 邊坡抗滑樁設計計算的三維有限元法[J]. 巖石力學與工程學報，2012,31(12)：2572-2578.

[6] R.Kourkoulis, F.Gelagoti, I.Anastasopoulos, et al. Slope stability piles and pile-groups: parametric study and design insights[J]. Journal of Geotechnical and Geoenvironment Engineering, 2011, 137(7): 663-677.

[7] R.Kourkoulis, F.Gelagoti, I.Anastasopoulos, et al. Hybrid method for analysis and design of slope stability piles[J]. Journal of Geotechnical and Geoenvironment Engineering, 2012, 138(1): 1-14.

[8] Rocscience. User′s guide for Slide, version 6.0[Z]. Toronto, Canada: 2010.

[9] Geo-Slope International. GeoStudio: User′s guide for SLOPE/W, version 6.0[Z]. Calgary, Canada: 2004.

[10] 中華人民共和國行業標準編寫組. (TB 10025-2006)鐵路路基支檔結構設計規范[S]. 北京：中國鐵道出版社，2006.

[11] 中華人民共和國電力行業標準編寫組. (DL/T 5057-2009)水工混凝土結構設計規范[S]. 北京：中國電力出版社，2009.

[12] Ben Leshchinsky, A.M.ASCE, Spencer Ambauen. Limit equilibrium and limit analysis: comparison of benchmark slope stability problems[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015, 141(10): 1-8.

2017- 01- 15

孫博(1984-)，男，河北廊坊人，博士，工程師，從事水工設計工作。

TU470

A

1003-9805(2017)04-0008-03