射頻功率放大器冪級數模型的系統辨識與實現

仝 野

(南京郵電大學 通信與信息工程學院，江蘇 南京 210003)

射頻功率放大器冪級數模型的系統辨識與實現

仝 野

(南京郵電大學 通信與信息工程學院，江蘇 南京210003)

冪級數模型是描述無記憶功率放大器的一個常用模型，系數辨識是準確建立模型的關鍵因素。通過對功放非線性等特性的研究，探討辨識冪級數模型的最小二乘算法與卡爾曼濾波算法，對功放的實際應用具有一定的指導意義。研究了基于最小二乘法與卡爾曼濾波算法的射頻功率放大器冪級數模型的參數估計方法，進行了相應的數值仿真實驗，結果顯示：最小二乘算法具有計算簡單與容易實現的優點，而卡爾曼濾波算法計算量大，原理復雜，但當冪級數階數有限時，隨著迭代次數的增加，估算的準確度會更高。

射頻功率放大器；冪級數模型；系統辨識；最小二乘算法；卡爾曼濾波算法

0 引言

射頻功率放大器是現代無線通信體系中實際操作用到的基本器件之一，也是系統非線性的重要出處[1]，提高其線性性能是一項艱巨任務。由于實際需求，功放要工作在非線性區域才能使信號得到足夠的放大，導致了以前的小信號分析理論不能滿足現實的需要，特別是在射頻微波技術方面呈現的問題非常突出，這是目前亟待解決的重要難題。

要研究射頻功率放大器，首先要對功放進行數學建模。行為模型是功率放大器模型的一種重要類型，其又可以細分為：無記憶行為模型和有記憶行為模型[2]。冪級數模型是描述無記憶射頻功率放大器的一個簡單的常用模型。本課題通過對射頻功率放大器冪級數模型的分析，探討了辨識功放冪級數模型系數的幾種常用方法，對于功放的實際應用具有重要的指導意義。此外，冪級數模型也是一些功放記憶模型的基礎，如記憶多項式模型，因此掌握好冪級數模型對復雜模型有極大幫助。

1 PA冪級數分析模型

冪級數模型是描述無記憶功放最常用的分析模型，這里對它的一般形式進行歸納。使用冪級數對功放建模時，功放的輸入信號與輸出信號可以用下面的冪級數描述[3]：

(1)

式中，ci表示模型系數。冪級數模型特色是模型系數ci能夠表示功放輸出信號幅度的失真，進一步能夠推算系統的載波互調功率比，對于一般的非線性功放，只需取前三階即可滿足實際要求。當ci取復數時，冪級數模型不僅可以表示功放信號幅度變化，也能表示相位變化。

2 PA冪級數模型的系數辨識算法

2.1最小二乘算法

根據Weierstrass定理進行函數逼近，解析函數G(x)能夠用一個階次足夠大的多項式近似[4]，所以可以用下面公式描述：

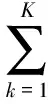
(2)

式中ck表示模型系數，x(n)表示輸入信號，f(n)表示輸出信號，K為非線性的階數。

但在實際應用時，通常并不直接采用式(2)，而是將其變形為:

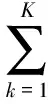
(3)

冪級數模型可以方便地用最小二乘算法辨識出其中的參數[5]。經實際測量可得功放的N對輸入、輸出數據值，令輸入信號序列記為x0,x1,x2,…,xN，輸出信號序列為f0,f1,f2,…,fN,則輸入、輸出矩陣分別為:

(4)

FN=(f0,f1,…,fN)T

(5)

將模型中的參數記為：

C=(c1,c2,…,ck)T

(6)

則式(1)可表示為如下矩陣方程:

FN=XN·C

(7)

(8)

其中上標H用來表示矩陣的共軛轉置。

2.2卡爾曼濾波算法

在用卡爾曼濾波算法辨識功放的參數時，首先要對系統進行建模。通常情況下，除了奇數階失真分量，其他失真分量均可用濾波器濾除，因此為了簡化起見，只考慮奇數階分量。功放奇數階冪級數數學模型表達式為：

(9)

其中M為非零自然數，b2i-1表示第2i-1個模型系數，則模型的階數為2M-1。奇數階冪級數模型形式簡單，系數容易識別。

如果令f2i-1(n)=s(n)s(n)2i-2，則式(9)可以改為：

(10)

將式(10)變換成矩陣形式：

x(n)=[Fn]Tb

(11)

其中[b]M×1=(b1,b3,…,b2M-1)T是模型系數矢量。

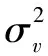
y(n)=[Xn]Th+v(n)

(12)

其中h=(h(0),h(1),…,h(Lh-1))T，[Xn]Lh×1是矩陣[X]Lx+Lh-1的第n行所有元素組成的列向量，其中Lx表示功放輸出序列長度，Lh表示有限長單位脈沖響應的長度，X具體描述為：

(13)

由式(13)知，[Xn]Lh×1=([Fn]Tb,[Fn-1]Tb,…,[Fn-Lh+1]Tb)T為矩陣形式。

若令：[Fn]MLh×1=([Fn]T,[Fn-1]T,…,[Fn-Lh+1]T)T，則有：

Xn=(I?b)T·Fn

(14)

其中符號“?”表示克羅內克積，那么輸入輸出關系可以寫為：

(15)

稱hb為擴展信道，并可知hb=h?b。由于射頻功放的非線性特性和信道的傳輸特性在一段時間內是不變的，那么擴展信道具有時間不變性，即：hb(n)=hb(n-1)。

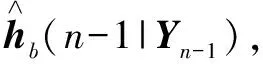
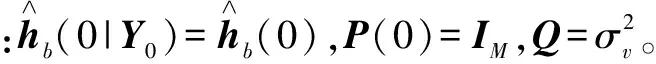
步驟1 卡爾曼濾波器估計擴展信道

時間更新：

(16)

P(n,n-1)=P(n-1)

(17)

狀態更新：

(18)

A(n)=Φ(n)P(n,n-1)ΦH(n)+Q

(19)

κ(n)=P(n,n-1)ΦH(n)A-1(n)

(20)

(21)

P(n)=(I-κ(n)A(n))P(n,n-1)

(22)

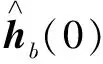
3 辨識算法的實現與比較

本節主要介紹利用最小二乘算法與卡爾曼濾波算法對特定的功率放大器冪級數模型進行系數識別。

3.1基于最小二乘算法的辨識實現

對功放的實際輸入輸出數據進行測量，得到此功放的一組觀測數據，通過MATLAB軟件仿真，可得到此功率放大器的輸入-輸出幅度變化圖，如圖1所示。

圖1 功放輸入-輸出幅度變化圖

功放冪級數模型表達式簡便，易于通過算法識別系數，且能夠直觀地表示非線性特性，公式為：

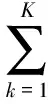
(23)

式中，K為非線性的階數。

冪級數模型中經常使用的是低階模型，簡單方便，不足是擬合準確度有限，但是若使用很高階數的模型，功放的輸出信號很可能出現“振蕩”[6]。所以，要想提高模型準確度，不能簡單增加冪級數階數。圖2是選取不同階數的冪級數進行仿真的結果。

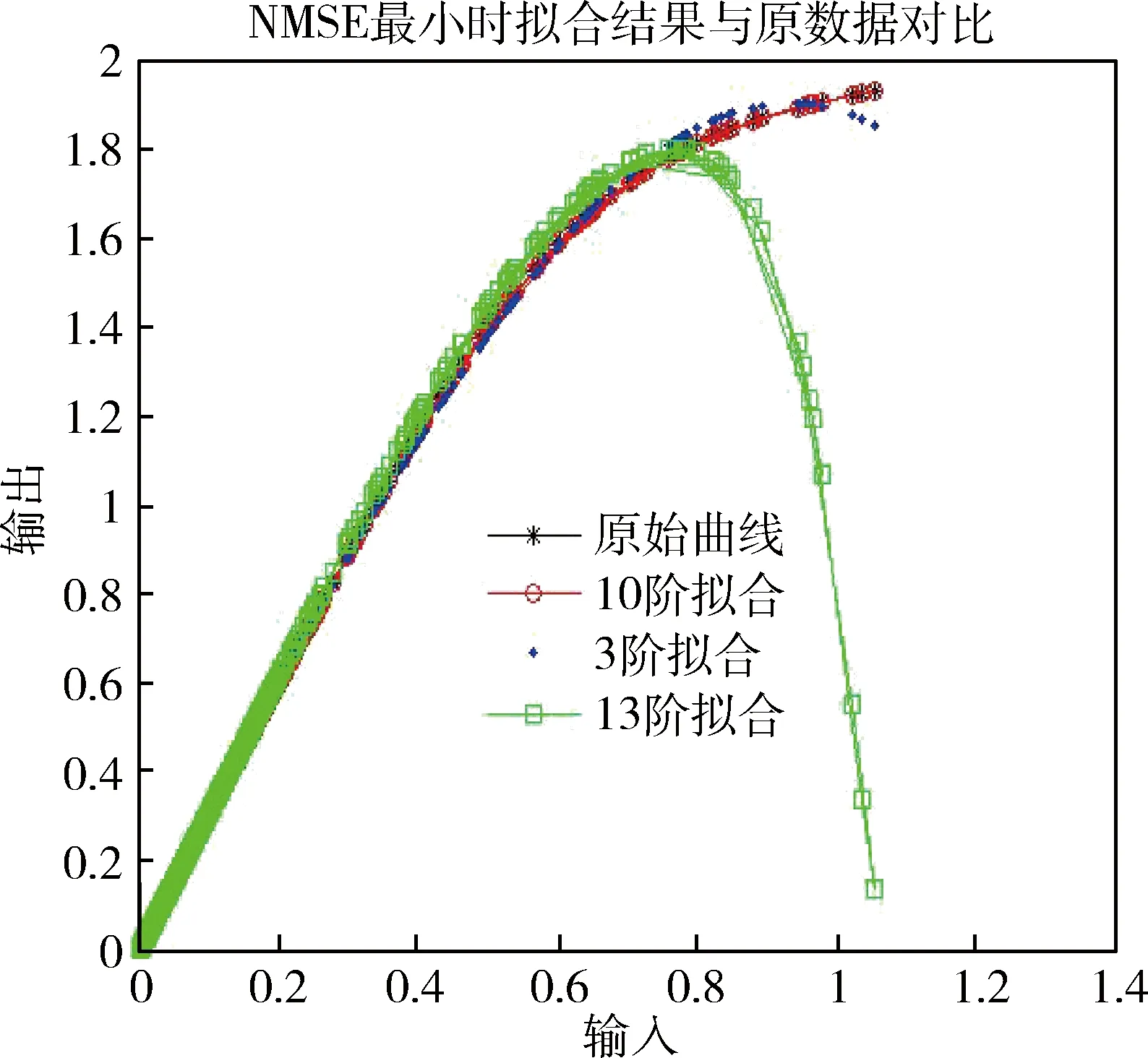
圖2 不同階數的冪級數模型擬合結果

由圖2可以看出階數為10時，模型的擬合效果最優。

在模型階數為10時，利用最小二乘算法得到的模型系數如表1所示。

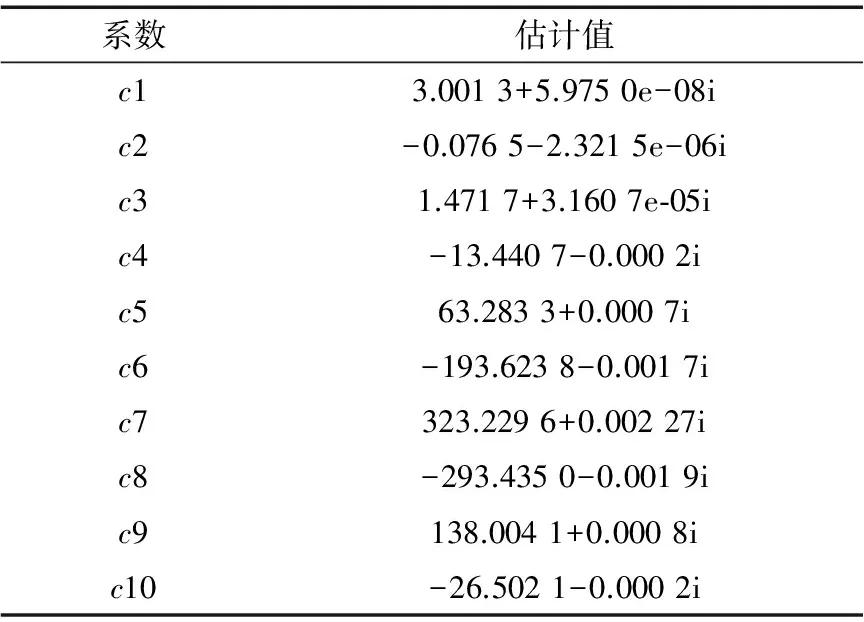
表1 模型系數

上面模型的計算結果通常使用歸一化均方誤差、誤差矢量幅度等指標來評價其精度。本文選用NMSE來評價無記憶功放模型的計算精度，具體定義如下：

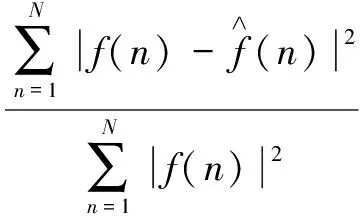
(24)

圖3是在不同階數下，采用NMSE功放輸出的擬合的精度曲線，橫軸為階數，縱軸為對應的NMSE值。

圖3 不同階數下NMSE曲線

從圖3中可以清楚地看到階次在20以下的各階次中，階數為10時，NMSE值最小，驗證了模型(23)階次取10時擬合精確度較高。

3.2基于卡爾曼濾波算法的辨識實現

OFDM是無線通信系統中一種傳輸技術，利用多信道多載波提高系統頻譜利用率，因采用多個子載波技術而能夠抗多徑衰弱。基于IEEE 802.11a協議的OFDM系統應用十分廣泛。由于支持IEEE 802.11a協議的無線局域網主要應用于室內，其信道是一個慢衰落信道，故而在一定時間內信道傳輸特性為恒定的。由IEEE 802.11a協議可知，OFDM的前導序列既有長序列也有短序列(10短2長)，其中長序列長度為160。

針對IEEE 802.11a協議，采用16-QAM調制的OFDM系統進行MATLAB仿真。使用室內經驗無線傳輸信道模型h(n)=0.996 0δ(n)+0.062 8δ(n-1)+0.007 9δ(n-2)，功放模型階數為5階，功率放大器冪級數模型系數如表2所示。依照協議產生長訓練序列，形成觀測集。

表2 功率放大器冪級數模型系數

擴展信道hb得到后就可以根據式(15)計算得到功放模型系數b。表3是第1 024次迭代估算出的模型系數值與真實值的比較，由此表可以看出隨著信噪比升高估算值越來越逼近真實值。

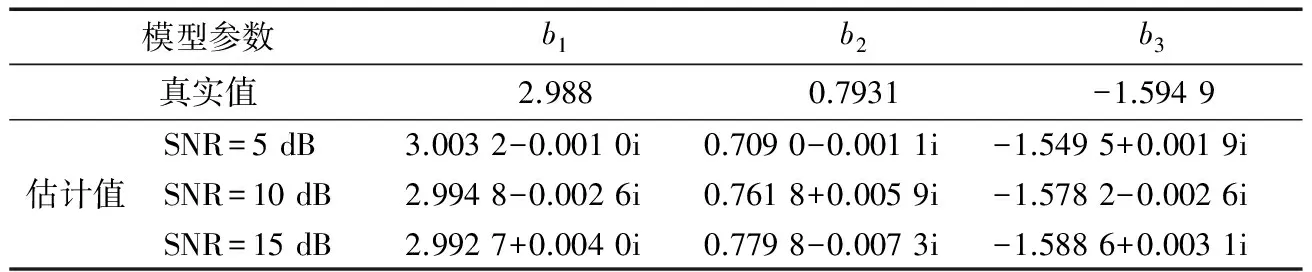
表3 估計值與實際值的比較

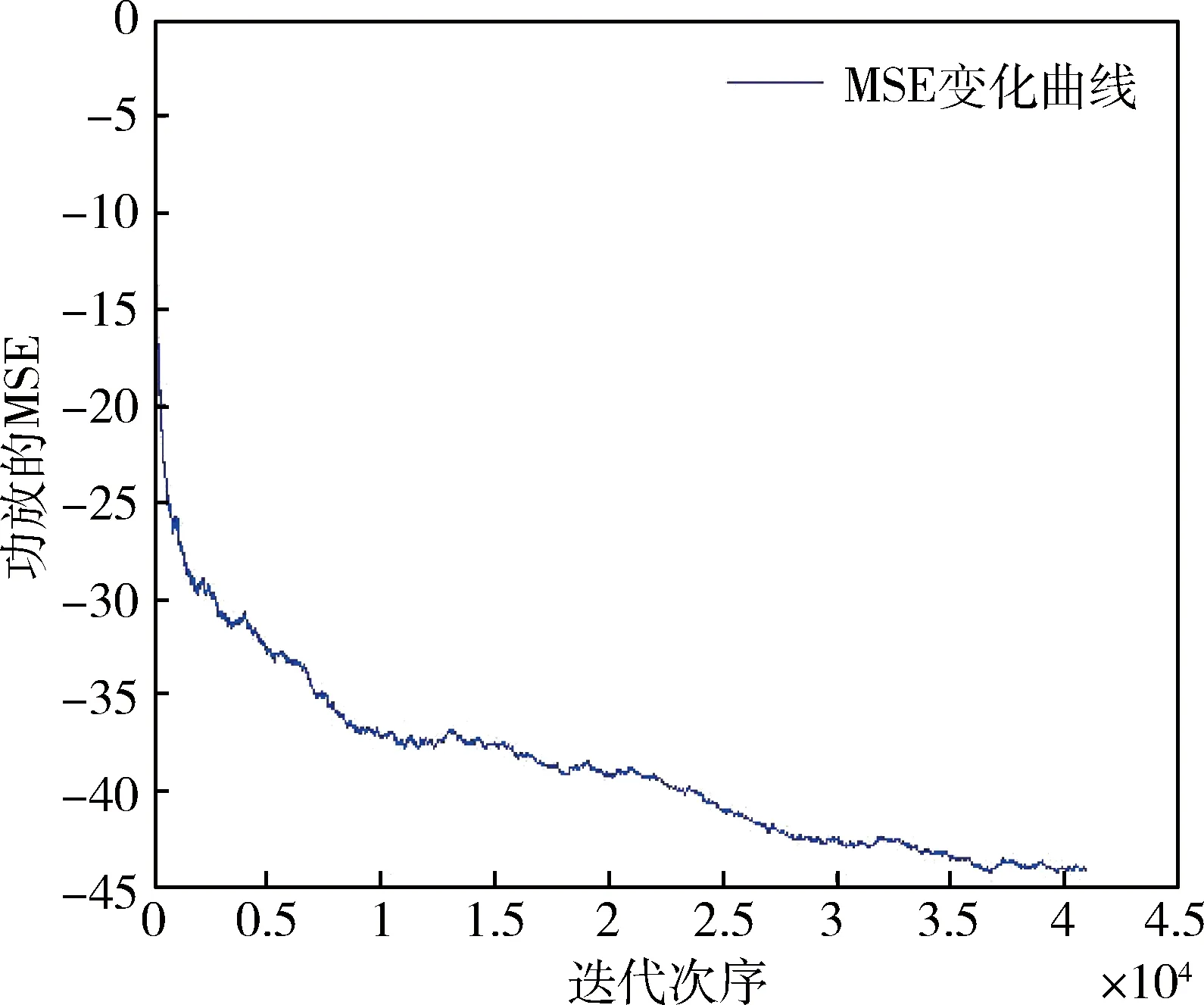
圖4 擴展信道均方誤差曲線

4 結論

通過以上兩節對實例的實際辨識可以得出，功放冪級數模型能夠方便有效地用最小二乘算法辨識出其中的參數，模型簡單，計算方便，實現起來也相對容易，冪級數模型中經常使用的是低階模型，簡單方便，不足是擬合準確度有限，但是若使用很高階數的模型，功放的輸出信號很可能出現“振蕩”。所以，要想提高模型準確度不能簡單增加冪級數階數。

采用卡爾曼濾波算法的系統模型相對復雜，需要借助信道實現冪級數模型系數的估算，計算量大，原理理解也相對困難，但當冪級數階數有限時，隨著迭代次數的增加，估算的準確度也在升高。系數估算的準確度也受信噪比影響，隨著信噪比升高，估算值也越來越逼近真實值。

綜上所述，上述兩種辨識方法各有其優缺點，應根據實際情況擇優選取。

[1] 郭陽. 高效射頻功率放大器數字預失真關鍵技術研究[D]. 成都: 電子科技大學, 2011.

[2] SABAGHI C, HADIANAMREI S, RAHNAMA M, et al. Using LDMOS transistor in class-F power amplifier for WCDMA applications[J]. International Journal of Communications, Network and System Sciences, 2011, 4(10)： 662-666.

[3] 祝樂芳. 功率放大器的非線性預失真技術的研究[D]. 沈陽: 沈陽理工大學, 2012.

[4] 高金輝,蘇明坤,李迎迎.基于ADS仿真的射頻功放設計[J]. 河南師范大學學報(自然科學版),2011,39(6): 48-50.

[5] 閆博. 基于ADS的射頻功率放大器設計與仿真[D]. 長沙: 國防科學技術大學, 2010.

[6] PARK C. Experimental investigation of differential line inductor for RF circuits with differential structure[J]. International Journal of Maritime Information and Communication Sciences,2011,9(1):11-15.

2017-04-19)

仝野(1993-)，男，碩士，主要研究方向：通信與信號處理。

System identification and realization of RF power amplifier based on power series model

Tong Ye

(College of Communication amp; Information Engineering, Nanjing University of Post amp; Telecommunication, Nanjing 210003, China)

The power series model is a common model for the description of the memoryless power amplifier, and the coefficient identification is the key factor to establish the model. Through the study of the nonlinear characteristics of the amplifier, the research on the least square algorithm and Kalman filtering algorithm with power series model has some guiding significance on the practical application of the power amplifier. This paper studies the estimation method of radio frequency (RF) power amplifier power series model parameters based on least square algorithm and Kalman filtering algorithm. We conduct the corresponding numerical simulation experiments, and the results show that the least square algorithm has an advantage of calculation and is easy to implement, while Kalman filtering algorithm calculation amount is large with complex principle. But when the order of the power series is limited, the accuracy of estimation will be higher with the increasing of iterations.

RF power amplifier; power series model; system identification; least square algorithm; Kalman filtering algorithm

TN722.75

A

10.19358/j.issn.1674- 7720.2017.22.020

仝野.射頻功率放大器冪級數模型的系統辨識與實現J.微型機與應用，2017,36(22)：74-77.