基于VMD和Infogram的滾動軸承故障特征提取

夏均忠， 于明奇， 黃 財， 汪治安， 呂麒鵬

(1.軍事交通學院 軍用車輛工程技術研究中心，天津 300161；2. 東莞市TR軸承有限公司，廣東 東莞 523000)

基于VMD和Infogram的滾動軸承故障特征提取

夏均忠1， 于明奇1， 黃 財2， 汪治安1， 呂麒鵬1

(1.軍事交通學院 軍用車輛工程技術研究中心，天津 300161；2. 東莞市TR軸承有限公司，廣東 東莞 523000)

帶通濾波器參數(中心頻率和帶寬)選取是共振解調的關鍵，針對快速峭度圖找尋的中心頻率偏大、帶寬過寬的問題，提出Infogram(信息圖)用于確定濾波器參數；并利用變分模態分解(Variational Mode Decomoposition, VMD)預先對信號進行重構，以減少噪聲對信息圖的影響，增強其應用效果。對軸承故障振動信號進行變分模態分解得到有限個模態分量，根據模態選取準則確定包含故障信息較多的模態分量進行信號重構，再應用信息圖確定最佳共振頻帶的中心頻率和帶寬，并對重構信號進行帶通濾波和包絡譜分析，識別軸承故障特征頻率。仿真分析和軸承外圈模擬故障試驗驗證了該方法的有效性。

滾動軸承； 特征提取； 快速峭度圖； 變分模態分解； 信息圖

滾動軸承廣泛用于旋轉機械中，其運行狀態是否正常往往直接影響整臺設備的性能，因此對滾動軸承技術狀態監測和早期故障診斷具有重要意義。滾動軸承通常由內圈、外圈、滾動體和保持架組成，當其中某一部分表面發生局部故障時，產生的脈沖會激起軸承及其相鄰部件的共振，產生調制現象[1]。在共振解調方法中，為獲得更好的解調效果，需要預先選取最優共振頻帶(中心頻率和帶寬)，以增強故障特征提取效果[2]。

譜峭度(Spectral Kurtosis，SK)及其基于短時傅里葉變換(Short-time Fourier Transform，STFT)的算法提出以來[3]，常用來確定最優共振頻帶的中心頻率和帶寬，但是基于STFT的譜峭度計算過程中，只使用一個固定窗，確定的中心頻率和帶寬不一定最優[4]。Antoni[5]引入峭度圖(Kurtogram)概念，提出快速峭度圖(Fast Kurtogram，FK)方法，使譜峭度得到迅速應用，但尋求的中心頻率偏大、帶寬過寬，導致在信號信噪比較低、含有隨機脈沖噪聲或者故障脈沖重復率較大等情況下容易失效，為此，增強或改進方法不斷提出。Guo等[6]將譜峭度與總體經驗模式分解相結合，增強了其應用效果。Lei等[7]認為對于處理非平穩瞬態振動信號，小波包變換要優于STFT，因此利用小波包變換代替了STFT，改進了譜峭度算法。Tomasz Barszcz提出突起度圖(Protrugram)方法，該方法基于窄帶包絡譜幅值的譜峭度指標，其應用效果優于快速峭度圖[8]，但未給出理論上的合理證明，且帶寬需要預先確定[9]。Antoni引入譜負熵(Spectral Negentropy)概念，提出信息圖(Infogram)方法，在含有隨機脈沖噪聲和故障脈沖重復速率較大等情況下取得了較好效果[10]，但仍受噪聲干擾，未能達到理想效果[11]。

為了有效降低噪聲對信息圖的影響，提高識別的可靠性，本文提出一種基于變分模態分解和信息圖的滾動軸承故障特征提取新方法。首先對采樣信號進行變分模態分解，(Variational Mode Decomoposition，VMD)，然后根據模態選取準則確定模態分量進行重構，再根據信息圖方法確定帶通濾波器參數，對重構信號帶通濾波和包絡解調分析完成故障特征提取，并通過仿真和試驗進行分析驗證。

1 變分模態分解

1.1 基本算法

變分模態分解是一種自適應信號處理新方法[12]，該方法在獲取分解分量的過程中通過迭代搜尋變分模型最優解來確定每個分量的頻率中心及帶寬，從而能夠自適應地實現信號的頻域剖分及各分量的有效分離。算法實現過程如下：

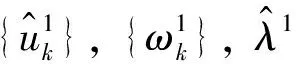
步驟2執行循環，n=n+1；

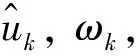
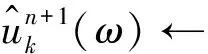
(1)

(2)

步驟4更新λ，k∈{1,K}

(3)

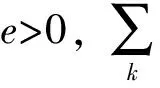
1.2 模態選取準則

信號經變分模態分解后可得到多個模態分量，但部分模態中故障成分不突出或者受到干擾較大，對故障特征提取無意義，因此要篩選出敏感模態以獲得最佳重構信號。本文提出一種基于峭度指數的模態選取準則[13]，峭度指數r可通過式(4)進行計算

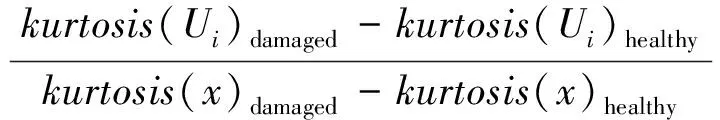
(4)

式中：kurtosis()為峭度計算函數；Ui(i=1,2,…,k)為模態分量；x為采樣信號。r值越大，模態中故障沖擊成分越突出，該模態也就越敏感。

計算各個模態的r值，并按其由大至小順序對相應模態分量排列，依次累加進行重構，直至重構信號與原始故障信號的相關系數達到90%以上。

2 信息圖

故障脈沖的出現，意味著打破了系統正常時的狀態平衡，系統熵值也會發生變化。定義信號頻帶上的熵值為譜熵(Spectral Entropy)。當軸承正常狀態時，信號的能量波動為常量，譜熵值最大，反之，當故障脈沖引起能量波動變化時，譜熵值最小，這與峭度指標變化恰好相反。為使其具有與譜峭度相同的物理意義，取譜熵負值定義為譜負熵。

定義長度為L的離散時域信號x(n)(n=0,…,L)，其頻帶[f-Δf/2,f+Δf/2]上的平方包絡SEx(n;f,Δf)

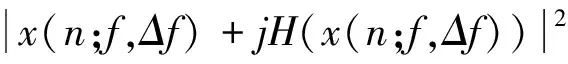
(5)

式中，H(·)為希爾伯特變換。時域中的譜負熵定義為

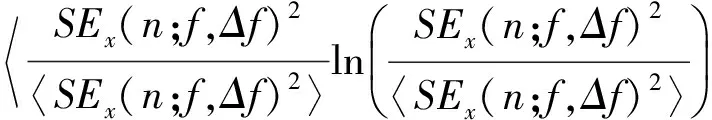
(6)

式中， 〈·〉為均值運算。時域中的譜負熵可以看作是權重為ln(SEx(n;f,Δf)2/〈SEx(n;f,Δf)2〉)的譜峭度， 因此ΔIe(f;Δf)可以用于表征頻帶[f-Δf/2,f+Δf/2]上因局部故障引起的脈沖特性。

除脈沖特性外，局部故障也表現出循環平穩特性，可用頻域中的譜負熵ΔIE(f;Δf)度量

ΔIE(f;Δf)=

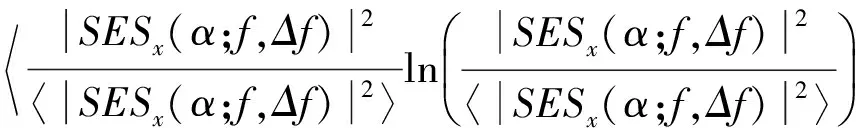
(7)

式中，SESx(α;f,Δf)為頻帶[f-Δf/2,f+Δf/2]上的平方包絡譜

SESx(α;f,Δf)=F(SEx(n;f,Δf))

(8)

式中：F(·)為傅里葉變換；α為頻率變化值，即循環頻率。

與快速峭度圖相同，為便于表示與計算上述譜負熵，提出基于STFT的算法：

(1) 構建濾波器組，中心頻率fs×(m+2-1)×2-υ-1，(m=0,1,…,2υ-1)和帶寬fs×2-υ-1(υ為分解層級，fs為采樣頻率)；

(2) 分解信號，利用濾波器組將信號分解為不同層級下(υ=0,1,1.6,2,2.6,3,3.6等)的次頻帶信號；

(3) 計算不同次頻帶信號的譜負熵值，時域中所有譜負熵值圖像表示為平方包絡信息圖(Square Envelope Infogram，SE Infogram)，頻域中所有譜負熵值圖像表示為平方包絡譜信息圖(Square Envelope Spectrum Infogram，SES Infogram)。

3 故障特征提取流程

與快速峭度圖相比，應用Infogram診斷機械故障雖然取得了較好成效，但采取某些信號預處理手段可以進一步提高應用效果。VMD法能有效克服經驗模態分解(Empirical Mode Decomposition，EMD)算法中的模態混疊及偽分量等問題[14]，其重構信號信噪比更低，能有效減少低頻干擾，突出高頻共振成分，而信息圖本身對共振頻帶的優選能力強于快速峭度圖，將兩者結合，有望取得更好的效果。為此，本文提出一種基于VMD和Infogram的滾動軸承故障特征提取方法，如圖1所示。具體算法步驟如下：

步驟1輸入信號，進行VMD分解；

步驟2根據模態選取準則選取敏感模態，累加重構；

步驟3應用SE Infogram、SES Infogram對重構信號的共振頻帶進行優選；

步驟4帶通濾波，求其平方包絡譜，從中輸出故障特征頻率，提取故障特征。

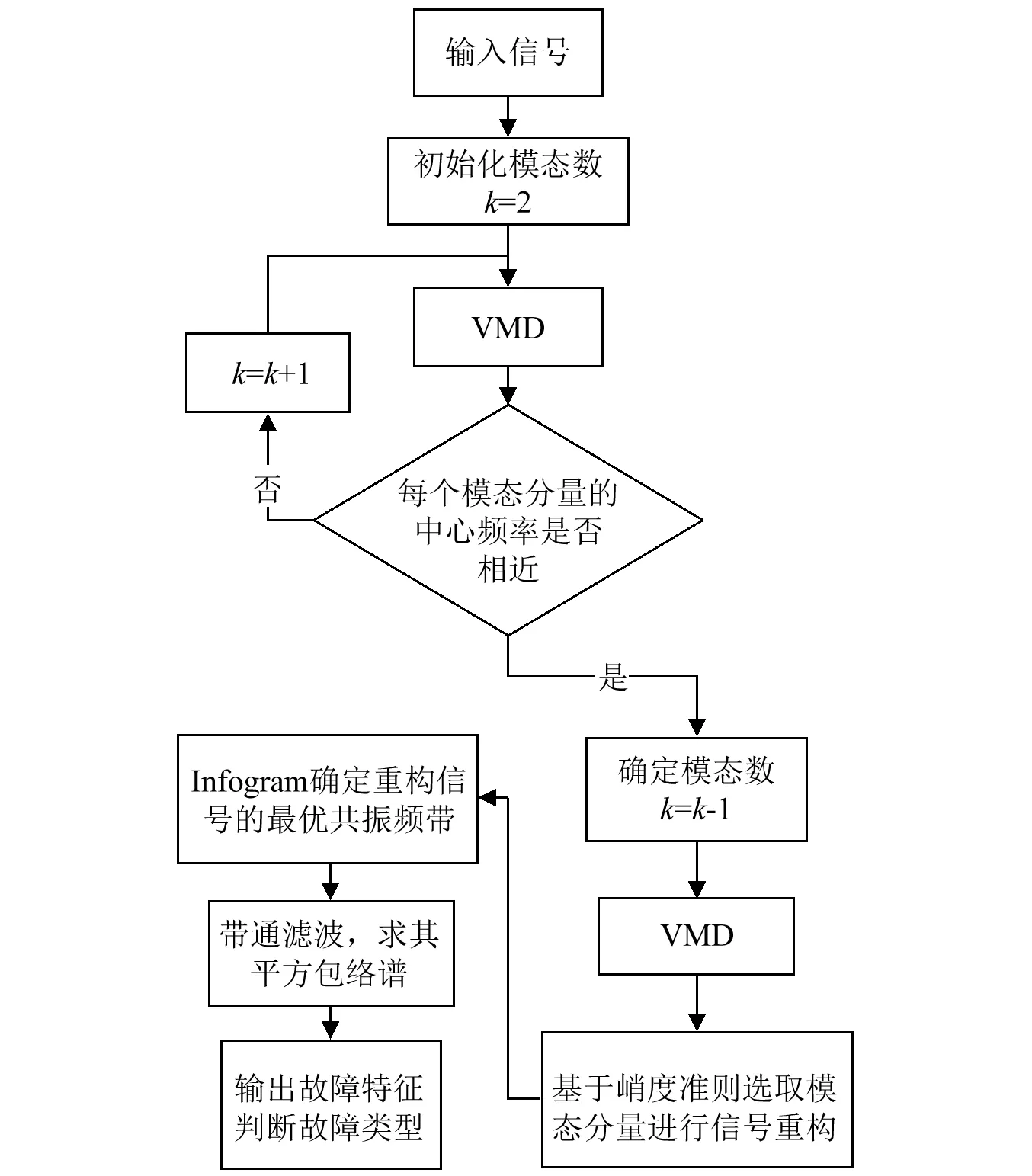
圖1 滾動軸承故障特征提取算法流程Fig.1 Flow chart of fault feature extraction for rolling element bearing

4 仿真分析

構造周期性振動脈沖仿真信號。單周期脈沖仿真信號x(t)表達式為

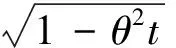
(9)

式中： 載波頻率fn=1 700 Hz; 位移常數x0=3； 阻尼系數θ=0.1；t為采樣時刻； 采樣頻率fs=12 000 Hz。 設置重復周期T=0.01 s， 即故障特征頻率fc=100 Hz，生成周期性振動脈沖信號， 如圖2(a)所示。添加隨機噪聲，其加噪仿真信號如圖2(b)所示。

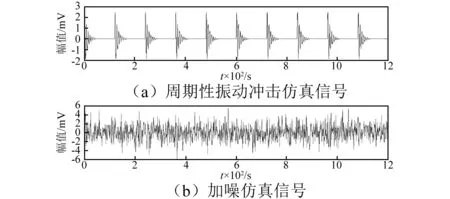
圖2 仿真信號時域波形Fig.2 Time domain waveform of simulated signal

首先利用VMD對加噪仿真信號進行分解，通過循環比較，可以確定模態數k=4時分解效果最佳，其分解后模態分量的時域波形，如圖3所示。從圖3可知，U2、U3和U4模態的時域波形盡管受噪聲干擾較大，但仍能辨別出故障沖擊成分的存在。計算各個模態的峭度指數r值， 如圖4所示。橫坐標分別為模態U1、U2、U3和U4，縱坐標表示峭度指數。從圖4可知，U2的r值最大，其次分別是U3、U4和U1，即模態U2中包含故障沖擊成分最為突出。

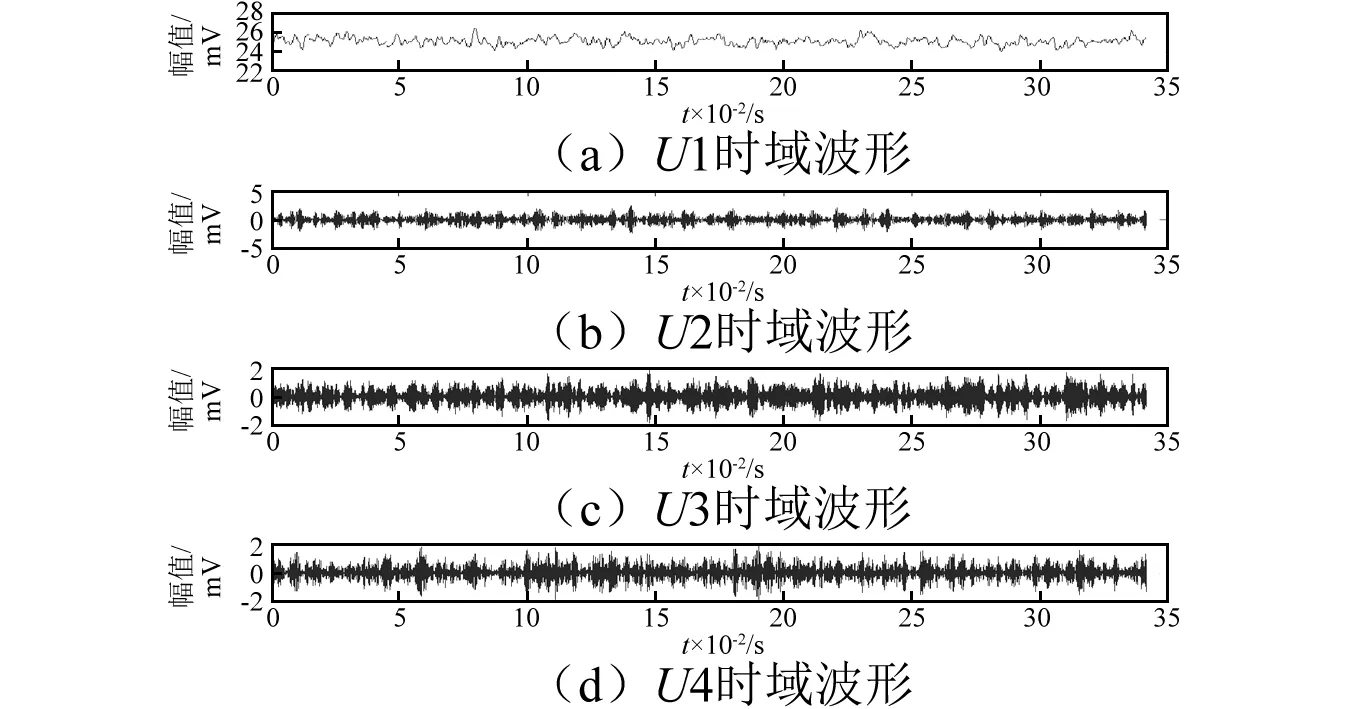
圖3 模態分量時域波形Fig.3 Time domain waveform of modes

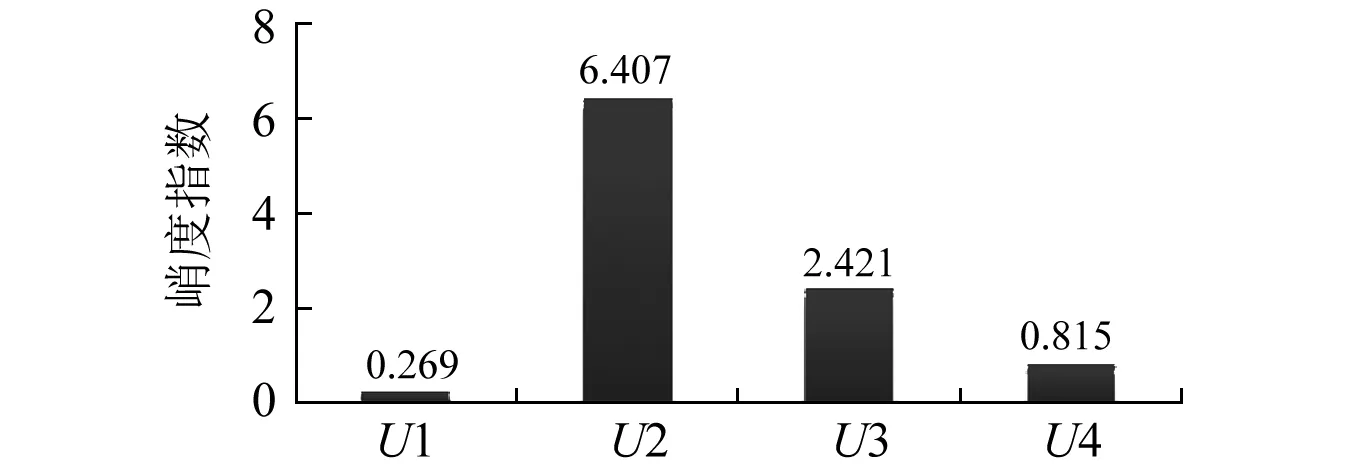
圖4 模態分量峭度指數值Fig.4 The kurtosis index of modes

各模態分量的包絡譜如圖5所示。從模態U2的包絡譜中可以明顯辨別出故障特征頻率及其諧波，而模態U3和U4的包絡譜比較模糊，模態U1包絡譜中無法識別故障信息，這說明了峭度指數r能夠表征模態中故障沖擊成分的存在。

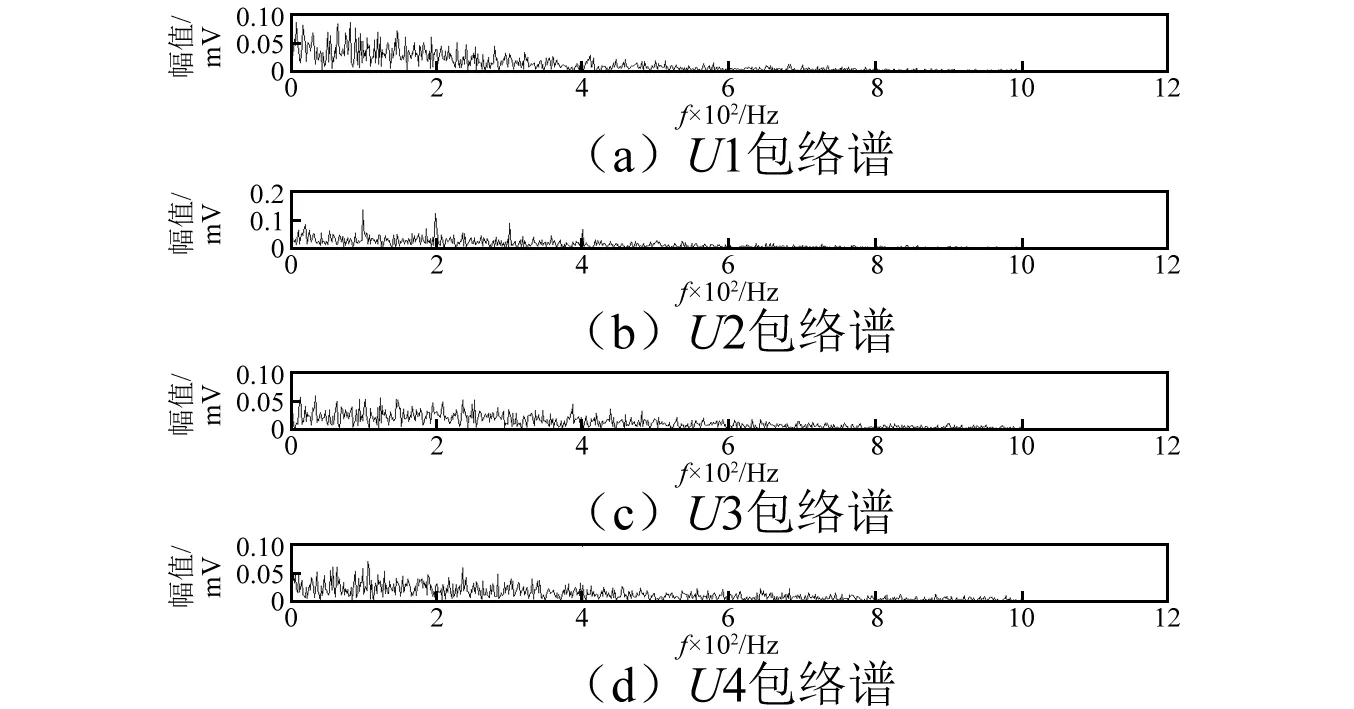
圖5 模態分量包絡譜圖Fig.5 The envelope spectrum of modes

按r值大小順序，對相應模態累加重構，當累加到U4時重構信號與原始信號的相關系數大于90%，停止累加，其重構信號的包絡譜如圖6所示。從圖6可較清晰地判斷出故障特征頻率fc(99.61 Hz)及其諧波(200.7 Hz、298.8 Hz)，但由于受噪聲干擾，譜圖中的故障特征不是十分突出。

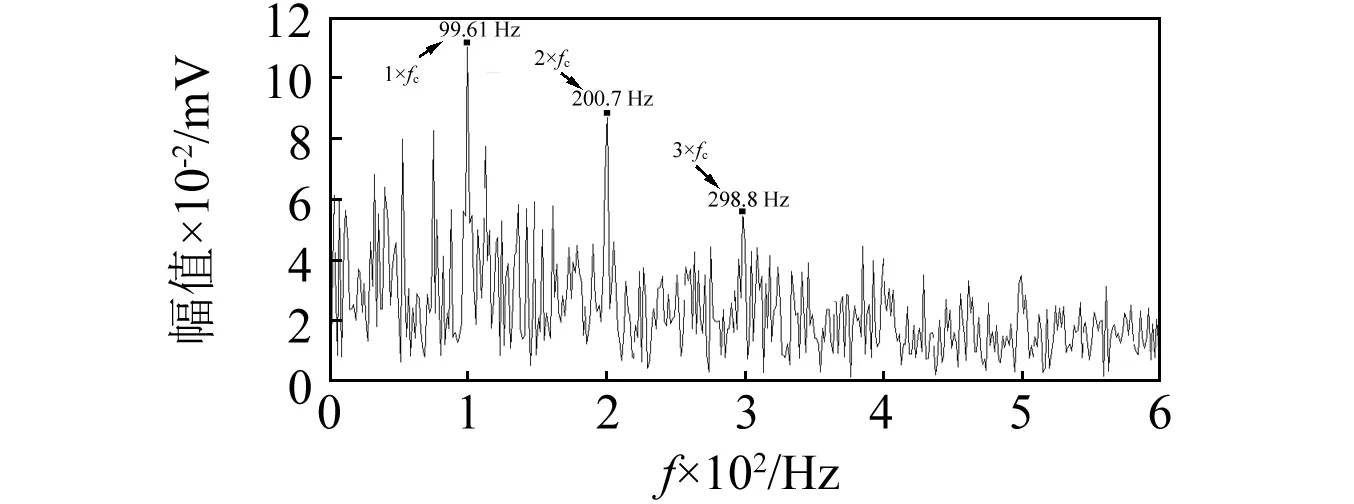
圖6 重構信號包絡譜圖Fig.6 The envelope spectrum of the reconstructed signal

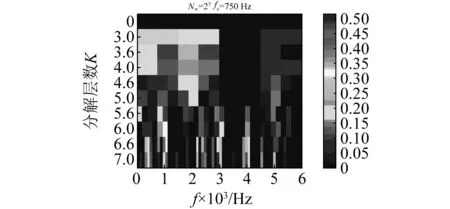
利用SE Infogram、SES Infogram對重構信號中的共振頻帶進行優選，如圖7所示。

(a) SE Infogram

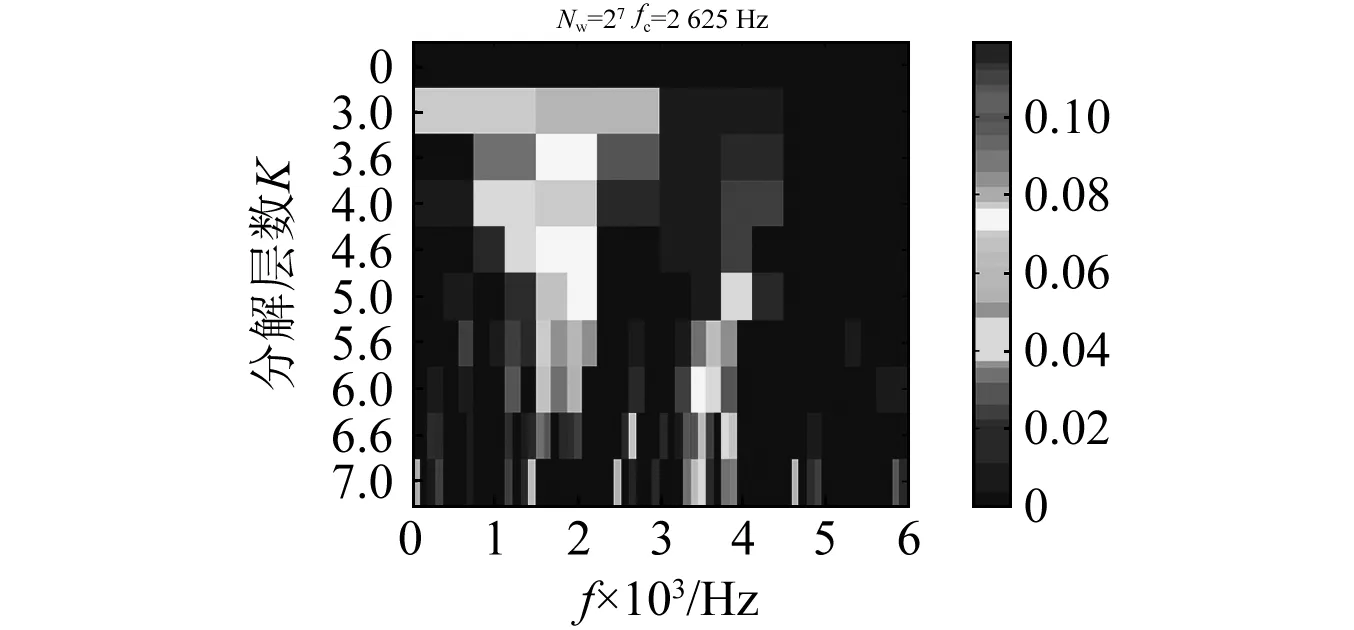
(b) SES Infogram圖7 重構信號信息圖Fig.7 Infogramof the reconstructed signal

調制現象的存在使得信號中包含多個共振頻帶，而SE Infogram、SES Infogram對信號中故障沖擊成分的識別性質不同，導致二種方法確定的共振頻帶不同，在實際應用中，可分別對比其應用效果，從中選擇最佳方法。應用SE Infogram、SES Infogram確定共振頻帶的帶寬均為27Hz，中心頻率分別為750 Hz、2 625 Hz，用上述參數構建帶通濾波器分別對該重構信號進行帶通濾波，計算其濾波信號的平方包絡，并對其平方包絡進行傅里葉變換得到平方包絡譜，如圖8所示。

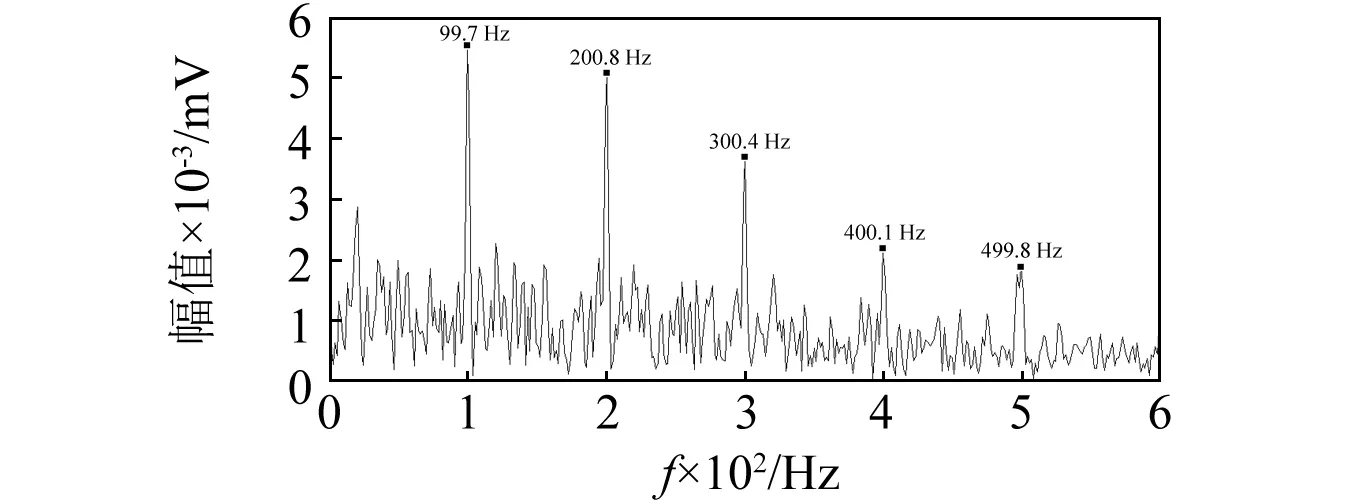
(a) 應用SE Infogram優選共振頻帶

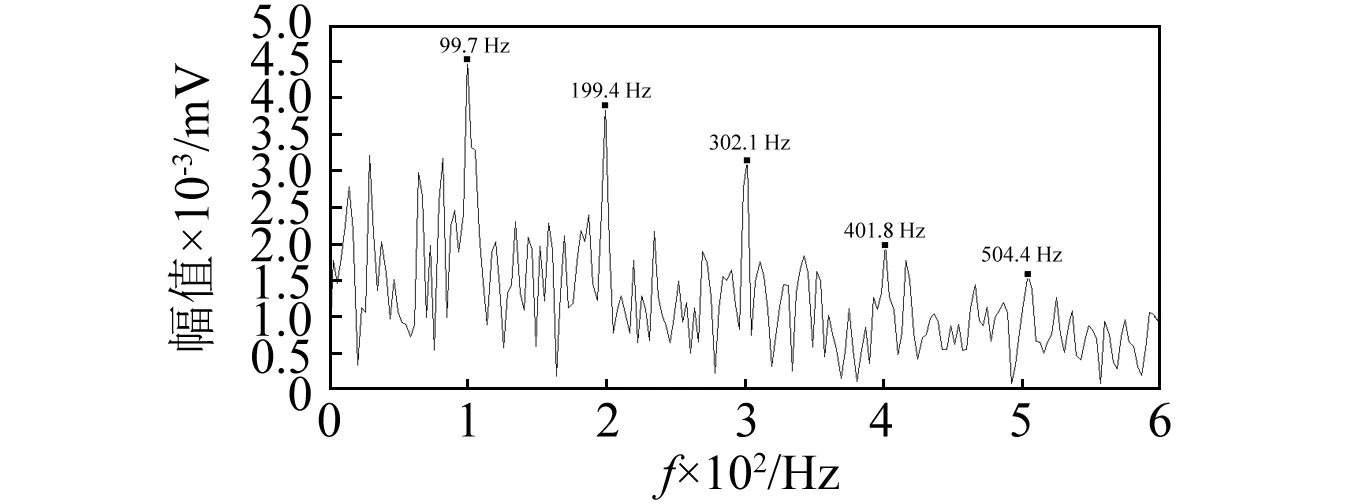
(b) 應用SES Infogram優選共振頻帶圖8 重構信號平方包絡譜Fig.8 Squared envelope spectrum of the reconstructed signal

從圖8可清晰辨識故障特征頻率及其諧波，尤其是SE Infogram應用效果最為理想：故障特征最為突出，故障沖擊的衰減性質也十分明顯。

下面分析比較信息圖與快速峭度圖的應用效果。利用快速峭度圖處理該重構信號，如圖9所示。快速峭度圖確定共振頻帶的中心頻率為93.75 Hz，帶寬為187.5 Hz，其平方包絡譜，如圖10所示。圖10中虛線位置為故障特征頻率(100 Hz)及其諧波。該譜圖中不存在與虛線重合的諧波，說明對于該重構信號，快速峭度圖失效。

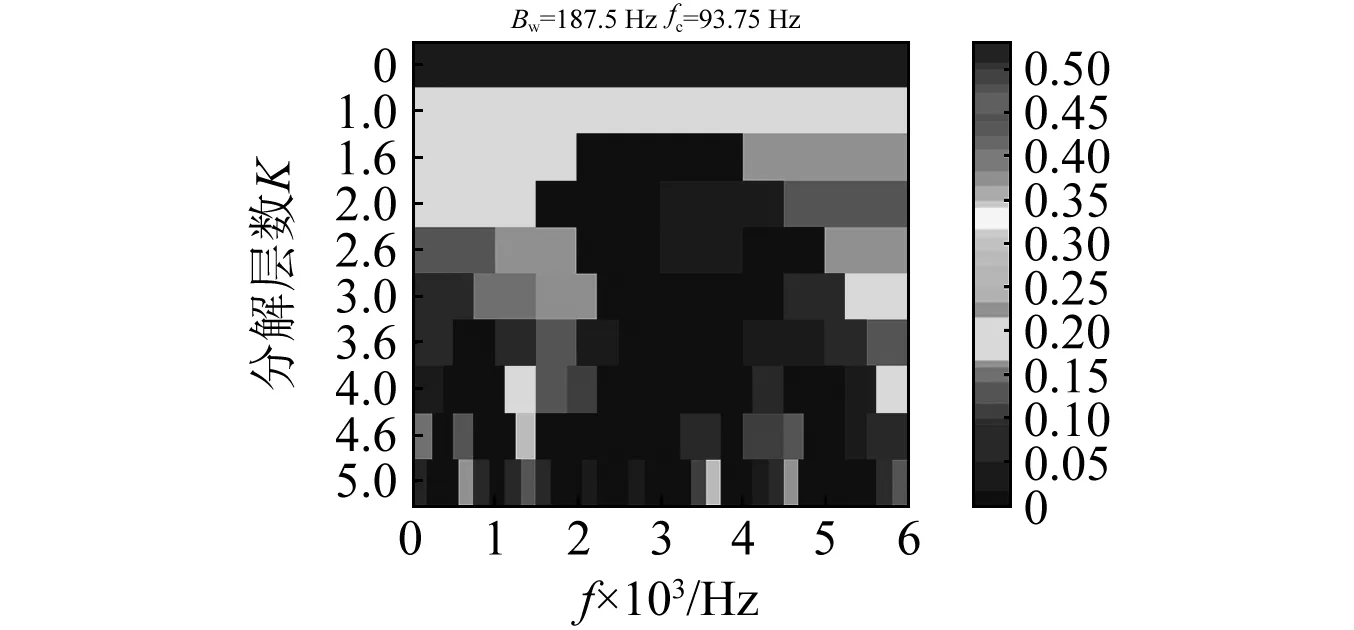
圖9 重構信號快速峭度圖Fig.9 Fast kurtogramof the reconstructed signal

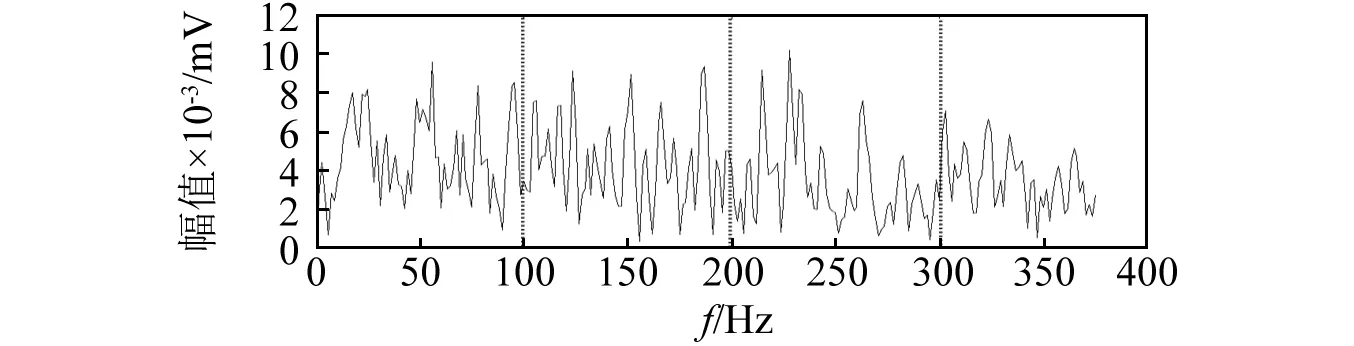
圖10 重構信號平方包絡譜(應用快速峭度圖選擇共振頻帶)Fig.10 Squared envelope spectrum of the reconstructed signal

基于信息圖的共振頻帶優選能力受噪聲等影響較大。利用VMD對原始信號進行預處理，能夠有效增強信息圖的辨別能力。為驗證VMD預先降噪對信息圖的影響，利用SE Infogram、SES Infogram直接對原始信號中的共振頻帶進行優選，確定共振頻帶的帶寬分別為26.5Hz、28Hz，中心頻率分別為3 187.5 Hz、609.37 Hz。其濾波信號的平方包絡譜如圖11所示。

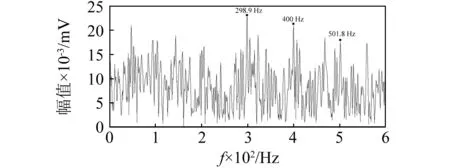
(a) 應用SE Infogram優選共振頻帶

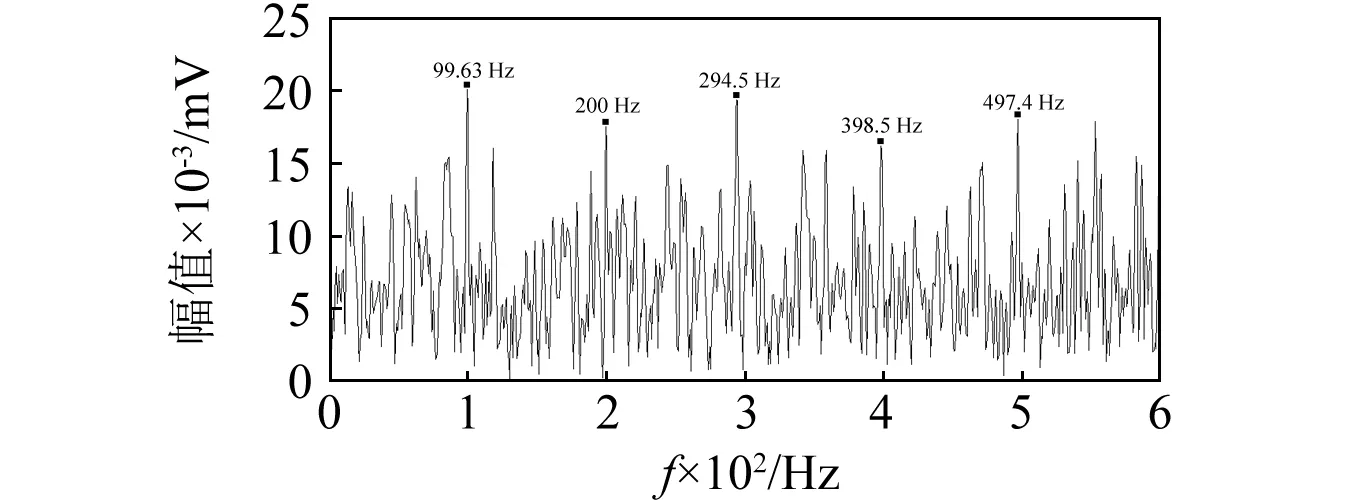
(b) 應用SES Infogram優選共振頻帶圖11 原始信號平方包絡譜Fig.11 Squared envelope spectrum of raw signal

由圖8、圖11可知，噪聲等影響信息圖對共振頻帶的選取能力，利用VMD預先降噪處理，可以增強信息圖的應用效果，有效突出高頻共振成分。

5 試驗驗證

試驗裝置由驅動電機、振動加速度傳感器、扭矩解碼/編碼器、聯軸器和功率計等組成，如圖12所示[15]。試驗軸承為SKF 6205-2RS深溝球軸承，支撐驅動電機驅動端，其技術參數見表1。

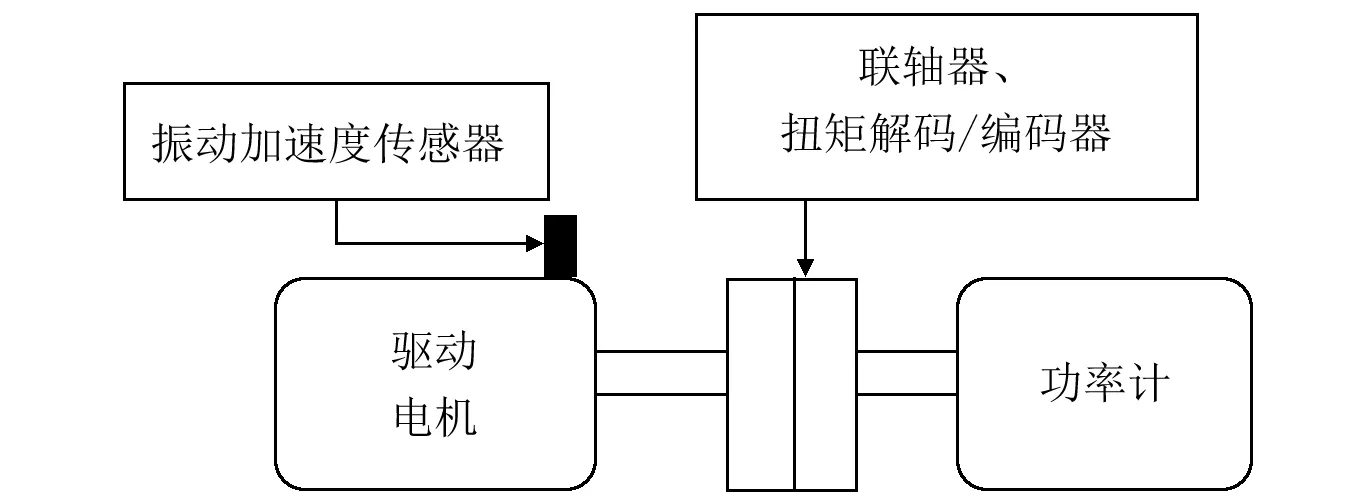
圖12 實驗裝置示意圖Fig.12 The schematic diagram of experimental device

表1 試驗軸承技術參數

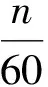
對采集的軸承外圈故障振動信號進行VMD分解，通過循環比較，確定分解模態數k=4，分解后計算各個模態的峭度指數r值，如圖13所示。按r值大小對相應模態降序排列，依次累加求和，當模態U4、U3、U2相加時，重構信號與原采集信號的相關系數達到92.31%，停止重構，得到重構信號。

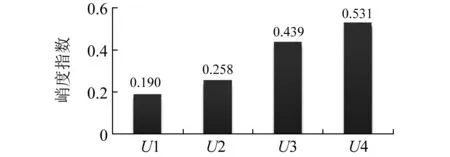
圖13 模態分量峭度指數值Fig.13 The kurtosis index of modes

分別應用快速峭度圖、信息圖對重構信號進行共振頻帶優選，如圖14、圖15所示。

快速峭度圖利用準解析濾波器組計算譜峭度。從圖14可以確定共振頻帶的中心頻率fc=5 250 Hz， 帶寬Bw=1 500 Hz， 其信號的平方包絡譜如圖16(a)所示。圖16中較難識別軸承外圈故障特征頻率(104.8 Hz)及其諧波(與理論值104.30 Hz不完全一致的原因是由于滾動體隨機滑動的影響)。

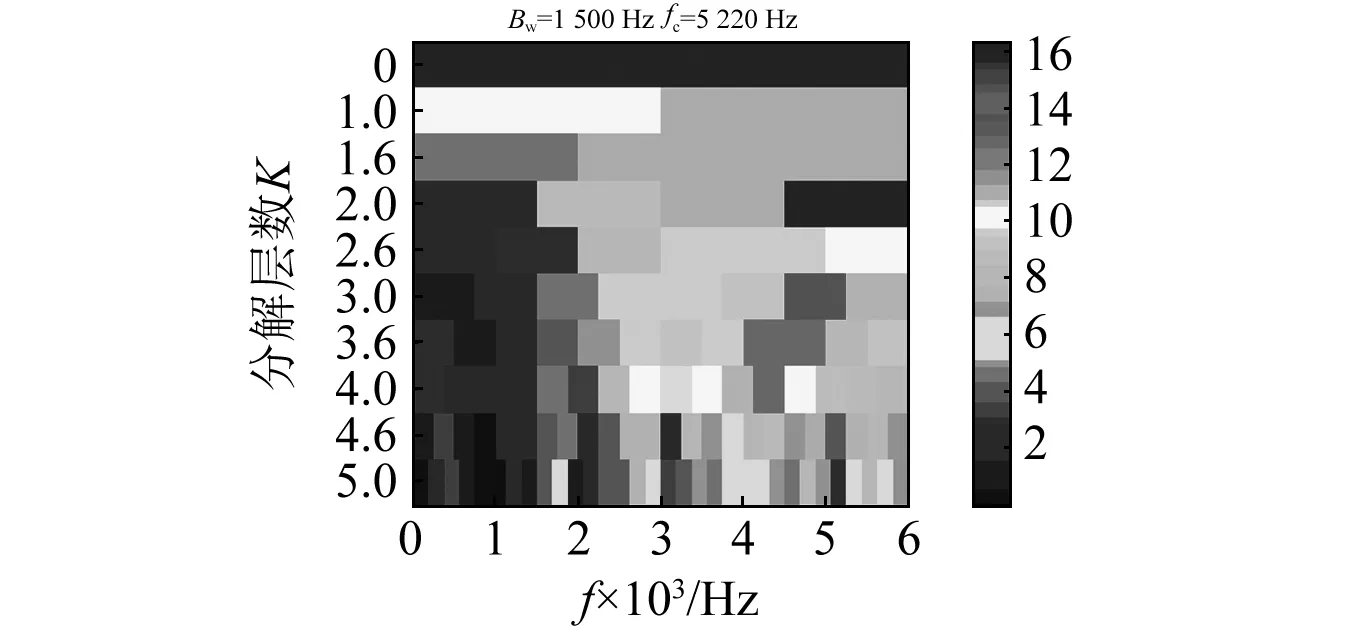
圖14 軸承外圈故障振動信號快速峭度圖Fig.14 Fast kurtogramof fault vibration signal of outer raceway

(a) SE Infogram

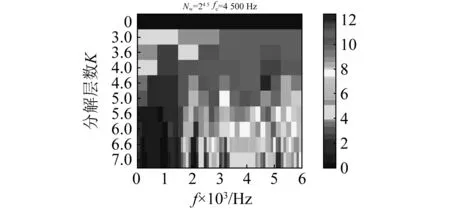
(b) SES Infogram圖15 軸承外圈故障振動信號信息圖Fig.15 Infogramof fault vibration signal of outer raceway

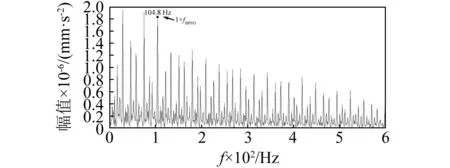
(a) 應用快速峭度圖優選共振頻帶

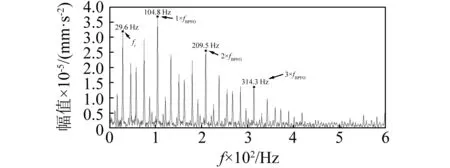
(b) 應用SE Infogram優選共振頻帶

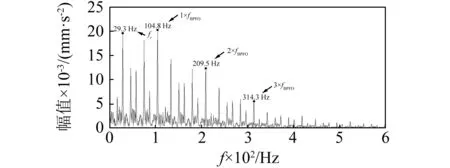
(c) 應用SES Infogram優選共振頻帶圖16 重構信號平方包絡譜Fig.16 Squared envelope spectrum of the reconstructed signal

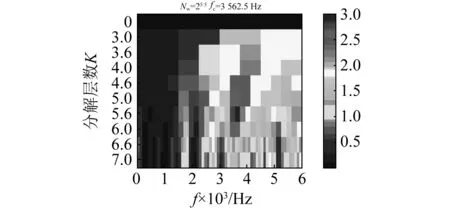
信息圖中，SE Infogram(見圖15(a))確定共振頻帶的中心頻率為3 562.5 Hz，帶寬為25.5Hz，其平方包絡譜如圖16(b)所示，從圖中，可以清楚辨認出故障特征頻率fBPFO(104.8 Hz)以及二次諧波(209.5 Hz)、三次諧波(314.3 Hz)和基頻fr(29.3 Hz)。

SES Infogram(見圖15(b))確定共振頻帶的中心頻率為4 500 Hz，帶寬為24.5Hz，其平方包絡譜如圖16(c)所示。從圖16(c)可以較清楚辨認出故障特征頻率fBPFO(104.8 Hz)以及二次諧波(209.5 Hz)、三次諧波(314.3 Hz)和基頻fr(29.3 Hz)及其諧波，但是與SE Infogram相比，譜圖中故障特征相對不是十分突出。

通過上述試驗分析對比，信息圖對故障信號中共振頻帶的優選能力強于快速峭度圖，并且利用VMD對信號分解重構，提高了重構信號信噪比，使得基于VMD和Infogram的滾動軸承故障特征提取方法取得了較理想的效果。

6 結 論

(1) VMD能夠解決EMD存在的模態混疊等問題，并表現出良好的噪聲魯棒性。通過對原始信號進行VMD分解重構，可有效突出高頻共振成分，減少信號中噪聲干擾，從而增強了信息圖的應用效果。

(2) 利用VMD分解信號時，可產生多個模態，敏感模態篩選方法層出不窮，但多數添加了主觀因素，導致篩選的不準確性，模態選取準則從峭度出發，考慮了故障與正常狀態峭度的相關關系，提出了量化指標——峭度指數，確保了篩選的準確性，并具有自適應性。

(3) 在共振解調中，快速峭度圖常用于優選共振頻帶，以增強解調效果，但在信號信噪比較低、含有隨機脈沖噪聲或者故障脈沖重復速率較大等情況下容易失效，信息圖方法的提出解決了該問題，并將與VMD結合，獲得了更好的解調效果，提高了軸承故障特征提取的準確性。

[ 1 ] 夏均忠，劉遠宏，李樹珉，等. 應用Hilbert變換和ZFFT提取變速器齒輪故障特征[J]. 振動與沖擊，2013，32(6): 63-66.

XIA Junzhong，LIU Yuanhong，LI Shumin，et al. Gearing fault detection using Hilbert transform and ZFFT[J]. Journal of Vibration and Shock, 2013, 32(6): 63-66.

[ 2 ] 王宏超，陳進，董廣明，等. 基于快速kurtogram算法的共振解調方法在滾動軸承故障特征提取中的應用[J]. 振動與沖擊，2013，32(1): 35-38.

WANG Hongchao，CHEN Jin，DONG Guangming，et al. Application of resonance demodulation in rolling bearing fault feature extraction based on fast computation of kurtogram[J]. Journal of Vibration and Shock, 2013, 32(1): 35-38.

[ 3 ] ANTONI J. The spectral kurtosis: a useful tool for characterizing nonstationary signals[J]. Mechanical Systems and Signal Processing, 2006, 20(2): 282-307.

[ 4 ] ANTONI J，RANDALL R B. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines[J]. Mechanical Systems and Signal Processing, 2006, 20(2): 308-331.

[ 5 ] ANTONI J. Fast computation of the kurtogram for the detection of transient faults[J]. Mechanical Systems and Signal Processing, 2007, 21(1): 108-124.

[ 6 ] GUO W，TSE P W，DJORDJEVICH A. Faulty bearing signal recovery from large noise using a hybrid method based on spectral kurtosis and ensemble empirical mode decomposition[J]. Measurement, 2012, 45(5): 1308-1322.

[ 7 ] LEI YG，LIN J，HE Z J，et al. Application of an improved kurtogram method for fault diagnosis of rolling element bearings[J]. Mechanical Systems and Signal Processing, 2011, 25(5): 1738-1749.

[ 8 ] BARSZCZ T，JABLONSKI A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the kurtogram[J]. Mechanical Systems and Signal Processing, 2011,25(1): 431-451.

[ 9 ] WANG D，TSE P W，KWOK L T. An enhanced kurtogram method for fault diagnosis of rolling element bearings[J].Mechanical Systems and Signal Processing, 2013,35(1/2): 176-199.

[10] ANTONI J. The infogram: entropic evidence of the signature of repetitive transients[J]. Mechanical Systems and Signal Processing, 2016, 74(1): 73-94.

[11] WANG D. An extension of the infograms to novel Bayesian inference for bearing fault feature identification[J]. Mechanical Systems and Signal Processing, 2016, 80(1): 19-30.

[12] DRAGOMIRETSKIY K，ZOSSO D. Variational mode decomposition [J]. IEEE Transaction on Signal Processing，2014，62(3): 531-544.

[13] KEDADOUCHE M，THOMAS M，TAHAN A. A comparative study between empirical wavelet transforms and empirical mode decomposition methods: application to bearing defect diagnosis[J]. Mechanical Systems and Signal Processing, 2016, 81(15): 88-107.

[14] 馬增強，李亞超，劉政，等. 基于變分模態分解和Teager能量算子的滾動軸承故障特征提取[J]. 振動與沖擊，2016，35(13): 134-139.

MA Zengqiang，LI Yachao，LIU Zheng, et al. Rolling bearing’ fault feature extraction based on variational mode decomposition and Teager energy operator[J]. Journal of Vibration and Shock, 2016, 35(13): 134-139.

[15] SMITH W A，RANDALL R B．Rolling element bearing diagnostics using the case western reserve university data：a benchmark study[J]．Mechanical Systems and Signal Processing, 2015, 64(2): 100-131.

FaultfeatureextractionofrollingelementbearingbasedonVMDandInfogram

XIA Junzhong1， YU Mingqi1， HUANG Cai2， WANG Zhian1， Lü Qipeng1

(1.Research Center of Military Vehicle Engineering amp; Technology，Academy of Military Transportation，Tianjin 300161, China；2. Dongguan TR bearing Co., Ltd., Dongguan 523000, China)

It is crucial to select the band-pass filter parameters (center frequency and bandwidth) for resonance demodulation. To overcome a problem occurred in fast kurtogram that both the center frequency and bandwidth are too large, an infogram was presented to select the filter parameters. The signal was reconstructed beforehand to reduce the influence of noise on the infogram. Firstly, roller bearing fault vibration signals were decomposed into a finite number of modes. Secondly, the modes containing rich fault information were selected according to the selection criterion of modes, then the center frequency and bandwidth of optimal resonance frequency band were selected with the help of the infogram. Finally, fault feature frequency was obtained by a band filter and envelope demodulation. The simulated signal and the measured outer fault signal of rolling bearing show that the proposed method is effective for fault feature extraction of rolling bearing.

rolling element bearing; fault feature extraction; fast kurtogram; variational mode decomoposition(VMD); Infogram

2016-12-01 修改稿收到日期： 2017-02-10

夏均忠 男，博士，教授，1967年生

于明奇 男，碩士生，1991年生

TN911.23；TB53

A

10.13465/j.cnki.jvs.2017.22.018