基于RBF神經網絡的SCR脫硝系統噴氨優化

廖永進， 范軍輝， 楊維結， 季 鵬， 張 靜， 馮永新

(1.廣東電網有限責任公司電力科學研究院，廣州 510080;2.華北電力大學 能源動力與機械工程學院，河北保定 071003)

基于RBF神經網絡的SCR脫硝系統噴氨優化

廖永進1， 范軍輝2， 楊維結2， 季 鵬2， 張 靜2， 馮永新1

(1.廣東電網有限責任公司電力科學研究院，廣州 510080;2.華北電力大學 能源動力與機械工程學院，河北保定 071003)

為實現對電廠選擇性催化還原(SCR)脫硝裝置噴氨的優化控制，以廣東某電廠350 MW鍋爐為研究對象，采用徑向基函數(RBF)神經網絡法，以鍋爐負荷、煙氣體積流量、SCR煙氣溫度、脫硝進口NOx質量濃度以及噴氨質量流量等為輸入變量，以SCR脫硝效率為輸出變量，建立輸入變量與輸出變量之間的關系模型，實現對SCR脫硝效率及脫硝出口NOx質量濃度的預測.在滿足NOx排放標準的前提下，以SCR系統運行成本最小為目標，利用Matlab對該模型進行仿真實驗，尋求氨耗成本和電耗成本與NOx排放費用的臨界點，得到最佳噴氨質量流量.結果表明：最佳噴氨質量流量計算值比實測值或高或低，但在滿足NOx排放標準的前提下，其SCR系統運行成本呈降低趨勢.

SCR； 噴氨質量流量； NOx排放； 脫硝效率； 成本

隨著社會經濟發展進程的不斷加快，我國NOx排放量不斷增加，因此面臨巨大的NOx減排壓力.據中國環境監測總站提供的數據，2011年我國NOx排放量為2 404.3萬t[1]，其中工業NOx排放量為1 729.7萬t，火電行業作為NOx排放的主要來源，在運行過程中產生的NOx占工業NOx排放量的一半以上.對此，環境保護部已實施了新的GB 13223—2011 《火電廠大氣污染物排放標準》[2]，并印發了《全面實施燃煤電廠超低排放和節能改造工作方案》，要求廣東等重點地區率先實現超低排放改造，即在基準氧體積分數為6%的條件下，煙塵、SO2和NOx排放質量濃度分別不高于10 mg/m3、35 mg/m3和50 mg/m3[3].

隨著環保部門對NOx排放量限制的日益嚴格，低NOx燃燒技術和煙氣脫硝技術被普遍應用于燃煤電站.選擇性催化還原(SCR)法在國內燃煤電站中的應用最為廣泛，具有脫硝效率高、技術成熟等優點[4-5].SCR法是指在催化劑、氧氣和一定溫度范圍條件下，還原劑(一般為氨)有選擇地將煙氣中的NOx(主要是NO)還原生成N2和H2O.影響SCR脫硝效率的主要因素有煙氣體積流量、SCR煙氣溫度、脫硝進口NOx質量濃度、噴氨質量流量以及催化劑活性等.根據實際運行情況來看，SCR煙氣溫度與鍋爐負荷和燃料燃燒情況有關，催化劑通常只能在失效后更換，因而噴氨質量流量成為可日常調整的關鍵因素之一[6].噴氨質量流量過小，難以保證達到NOx排放標準；噴氨質量流量過大，不僅造成NH3的浪費，而且在空氣預熱器中逃逸的NH3會與煙氣中的SO3和H2O反應生成NH4HSO4，而NH4HSO4有黏性，長時間堆積會引起堵灰現象[7-9].

盡管相關學者在優化控制噴氨方面進行了大量研究[10-15]，包括自動控制噴氨裝置的改進、噴氨方法的多樣化、改變脫硝出口NOx質量濃度分布以及降低氨逃逸率等，但以SCR系統運行成本最小為目標來優化控制噴氨的研究較少.王桂林等[16]基于支持向量機法建立了鍋爐運行過程中NOx生成和SCR脫硝效率的預測模型，以SCR系統運行成本最小為目標，利用遺傳算法對噴氨質量流量進行優化，實現了對噴氨的優化控制.但對于不同爐型，噴氨的優化控制存在差異，且該模型預測誤差相對較大.RBF神經網絡法已經被證明具有很強的非線性映射能力[17]，筆者以廣東某電廠350 MW鍋爐為研究對象，采用RBF神經網絡法建立SCR脫硝效率預測模型；以SCR系統運行成本最小為目標，利用Matlab對該模型進行仿真實驗，在滿足NOx排放標準的前提下獲得最佳噴氨質量流量.

1 研究對象及方法

1.1研究對象概況

廣東某電廠350 MW供熱抽汽凝汽式燃煤機組鍋爐是武漢鍋爐股份有限公司(AWBC)生產的亞臨界參數、自然循環、一次中間再熱、單爐膛平衡通風、固態排渣、露天布置、全鋼構架的∏型汽包爐，已安裝脫硝裝置，設計煤種為石圪臺煤，校核煤種1為神華混煤，參數如表1所示.采用SCR法，脫硝裝置按2+1層布置，設計脫硝效率不低于80%.SCR脫硝裝置催化劑采用蜂窩式催化劑，其主要參數如表2所示，脫硝系統進口煙氣設計值見表3.

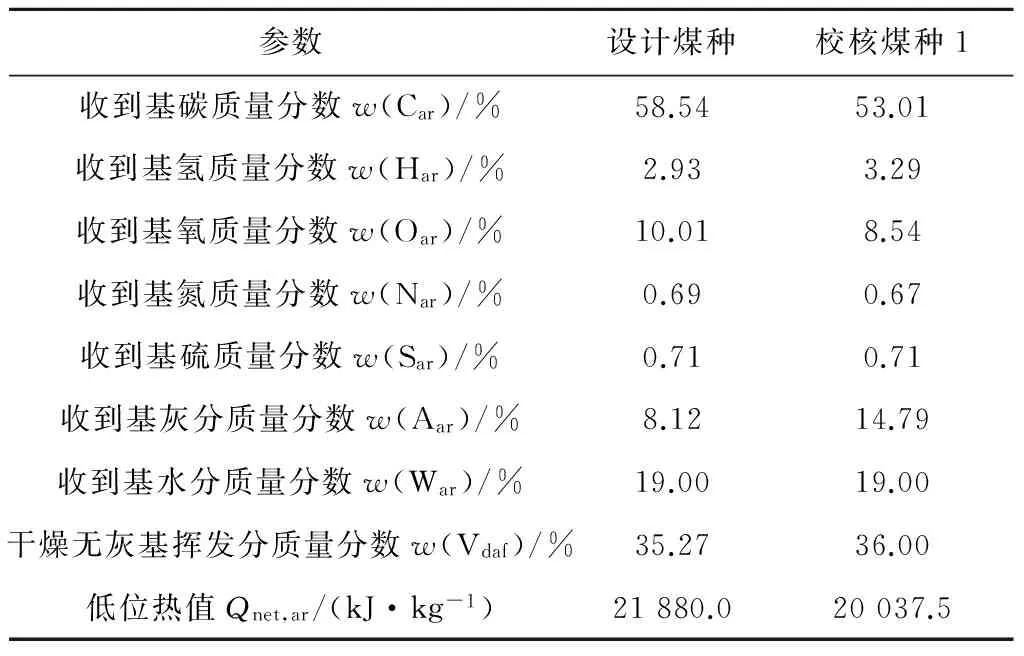
表1 煤質分析

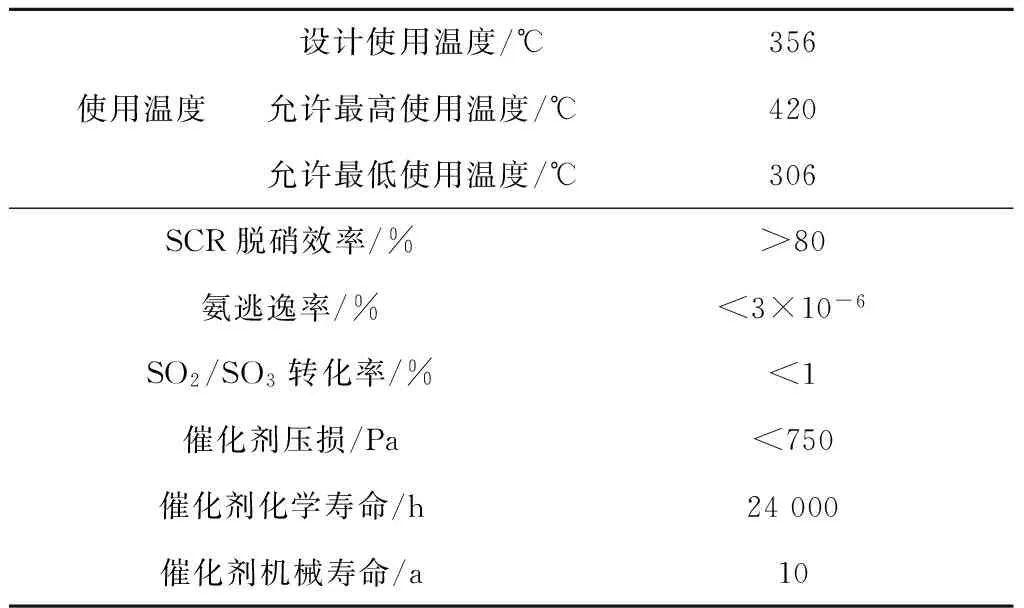
表2 催化劑主要參數

表3脫硝系統進口煙氣設計值(6%φ(O2)、標態、干基)

Tab.3Designparametersofinletfluegasinthedenitrificationsystem(6%φ(O2),standardstate,drybasis)

參數數值飛灰質量濃度/(g·m-3)36NOx質量濃度/(mg·m-3)400(設計值)SO2質量濃度/(mg·m-3)3150SO3質量濃度/(mg·m-3)38

1.2研究方法

筆者采用該機組的歷史運行數據，利用RBF神經網絡法建立SCR脫硝效率預測模型，預測出機組SCR脫硝效率以及脫硝出口NOx質量濃度，從而預測SCR系統運行成本.以SCR系統運行成本最小為目標，建立SCR系統運行成本關于噴氨質量流量的目標函數，利用Matlab對該模型進行仿真實驗，得到在滿足NOx排放標準前提下的最佳噴氨質量流量，實現對電廠SCR脫硝裝置噴氨質量流量的優化控制.

1.2.1 RBF神經網絡

RBF神經網絡基于正則化理論導出，具有收斂速度快、可逼近任意非線性函數等優點.其網格結構簡單，是一種3層前向網絡，第1層為輸入層，結點個數等于輸入的維數；第2層為隱含層，結點個數視問題復雜度而定；第3層為輸出層，結點個數為輸出層的維數，如圖1所示.RBF神經網絡結構屬于一種前饋網絡的拓撲結構，其輸入樣本向量先與權值向量相乘，再輸入到隱含層的節點，計算樣本與節點中心的距離，該距離經過徑向基函數的映射后形成隱含層輸出，再輸入到輸出層，各個隱含層節點(以下簡稱隱節點)的線性組合形成了最終的網格輸出[18].

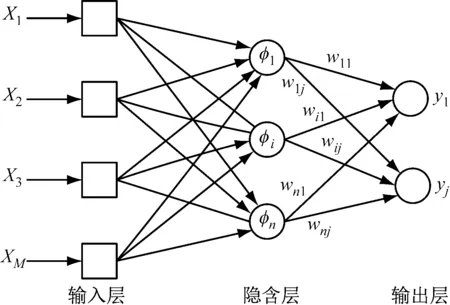
圖1 RBF神經網絡結構Fig.1 RBF neural network architecture

RBF神經網絡從輸入空間到隱含空間的變換是非線性的，而從隱含空間到輸出空間的變換是線性的.在實現RBF神經網絡由輸入到輸出的過程中，需要確定的主要參數為隱節點的中心及其標準差σ、徑向基函數的寬度、隱含層與輸出層間的權值矩陣.通常隱節點的中心可以采用聚類方法確定或直接從輸入樣本中選擇，而標準差σ可通過式(1)求得，隱含層與輸出層間的權值矩陣可通過求偽逆的方法得到.徑向基函數的寬度決定隱節點對外部輸入信號的相應范圍，當輸入信號靠近某個隱節點中心時，則該節點被激活，該節點將產生較大輸出；當輸入信號遠離此隱節點中心時，則該隱節點的輸出趨于0.徑向基函數僅對輸入信號產生局部響應，隱含層輸出在輸出層進行線性加權，實現從輸入空間到輸出空間的映射，從而使整個網絡達到分類或函數逼近的目的[17].

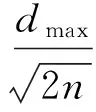
(1)

式中：dmax為選取隱節點中心之間的最大距離；n為隱節點個數，由OLS算法根據訓練樣本確定.

徑向基網絡與多層感知器不同，其隱含層為非線性，采用高斯函數作為徑向基函數.徑向基函數是一種局部分布的沿隱節點中心徑向對稱衰減的非負非線性函數，可用式(2)表示：

(2)

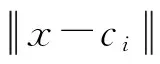
φi越小，說明徑向基函數的寬度越小，基函數的選擇性越強.網絡的第k個輸出可表示為：

(3)

式中：wki為隱含層神經元和輸出層神經元之間的權值矩陣；yk為實際輸出.

在應用RBF神經網絡的過程中，先確定所有隱節點中心ci，然后校正隱含層神經元與輸出層神經元之間的權值矩陣wki.

1.2.2 SCR系統運行成本計算

SCR系統運行成本包括氨耗成本、電耗成本、NOx排放費用、污染物排放達到標準后的電價補償以及人工、折舊、維修等費用[19]，其中污染物排放達到標準后的電價補償以及人工、折舊、維修等費用固定，而氨耗成本、電耗成本以及NOx排放費用均與噴氨質量流量相關.

根據模型輸入脫硝進口NOx質量濃度以及預測模型的SCR脫硝效率，計算脫除后NOx量，脫硝化學反應方程式為：

(4)

(5)

氨消耗質量流量qm,a(kg/h)為：

qm,a=[qV×ρNO×17/(30×106)+

qV×ρNO2×17×2/(46×106)]×m

(6)

ρNO=ρR，NOx/(2.05×0.95×1.34)

(7)

ρNO2=0.05×ρC,NOx

(8)

m=η/100+γa(ρNO/30+2ρNO2/46)/22.4

(9)

式中：ρNO、ρNO2分別為進口煙氣NO、NO2的質量濃度，mg/m3；ρR,NOx為脫硝進口NOx質量濃度；ρC,NOx為進口煙氣NOx的質量濃度；m為氨與SCR進口NOx質量濃度比；γa為氨逃逸率；qV為煙氣體積流量，m3/h；η為預測出的SCR脫硝效率.

結合氨水單價(3 000元/t)計算氨耗成本F1(元/h)：

F1=3×qm,a

(10)

根據噴氨質量流量及各脫硝設備總電流的相關數據，擬合出噴氨質量流量與各脫硝設備總電流之間的關系.一般情況下，噴氨質量流量越大，設備耗電量越大，可根據簡單的線性關系來擬合：

I=k×qm+b

(11)

式中：qm為噴氨質量流量；I為各脫硝設備總電流；k和b均為常數，可通過數據擬合得到.

根據噴氨質量流量估算出電耗成本，結合電價0.3元/(kW·h)計算電耗成本F2(元/h)：

F2=1.73×6 000×I×0.83×0.3÷1 000

(12)

根據脫硝進口NOx質量濃度及預測出的SCR脫硝效率η，可計算未脫除的NOx質量濃度.根據廣東省NOx排污費用征收標準，NOx排放費用為每當量2.4元，可計算排污費用F3(元/h).

未脫除的NOx質量濃度為：

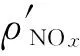
(13)

排污費用F3為：

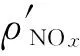
(14)

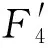
(15)

折合到單位時間，并統一單位，F4(元/h)可表示為：

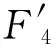
(16)

式中：P為鍋爐負荷.

其他成本包括人工、折舊、維修等費用，且基本固定，統一用G表示[20].將所有成本除以發電量，得到脫硝系統單位發電量總成本F(元·kW-1·h-1)，F可表示為：

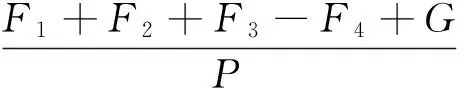
(17)

2 RBF神經網絡SCR脫硝效率預測模型

2.1建立預測模型

選取鍋爐負荷、煙氣體積流量、SCR煙氣溫度、脫硝進口NOx質量濃度以及噴氨質量流量等為輸入變量，以SCR脫硝效率為輸出變量，構造一個5輸入-1輸出的預測模型，如圖2所示.

圖2 SCR脫硝效率η的預測模型Fig.2 Prediction model of the SCR denitrification efficiency η

根據預測模型的需要，隨機選取100組數據作為訓練樣本(鍋爐負荷在50%～100%內)，25組數據作為測試樣本，訓練開始前先對數據進行濾波處理，篩除偏差較大的數據，然后利用Matlab神經網絡工具箱提供的newrb函數對構造的網絡模型進行訓練.在訓練過程中，由于newrb函數創建的徑向基網絡隱含層的節點不確定，因此根據設定的誤差目標向徑向基網絡中不斷添加新的隱節點，并調整節點中心、標準差及權值，直到網絡達到預期的誤差目標要求，設置誤差容限為10-8.根據newrb函數創建的徑向網絡在Matlab中仿真，得到SCR脫硝效率訓練誤差，如圖3所示.用view(net)命令得到最終的徑向基網絡結構，結構圖顯示隱含層包含198個神經元，如圖4所示.

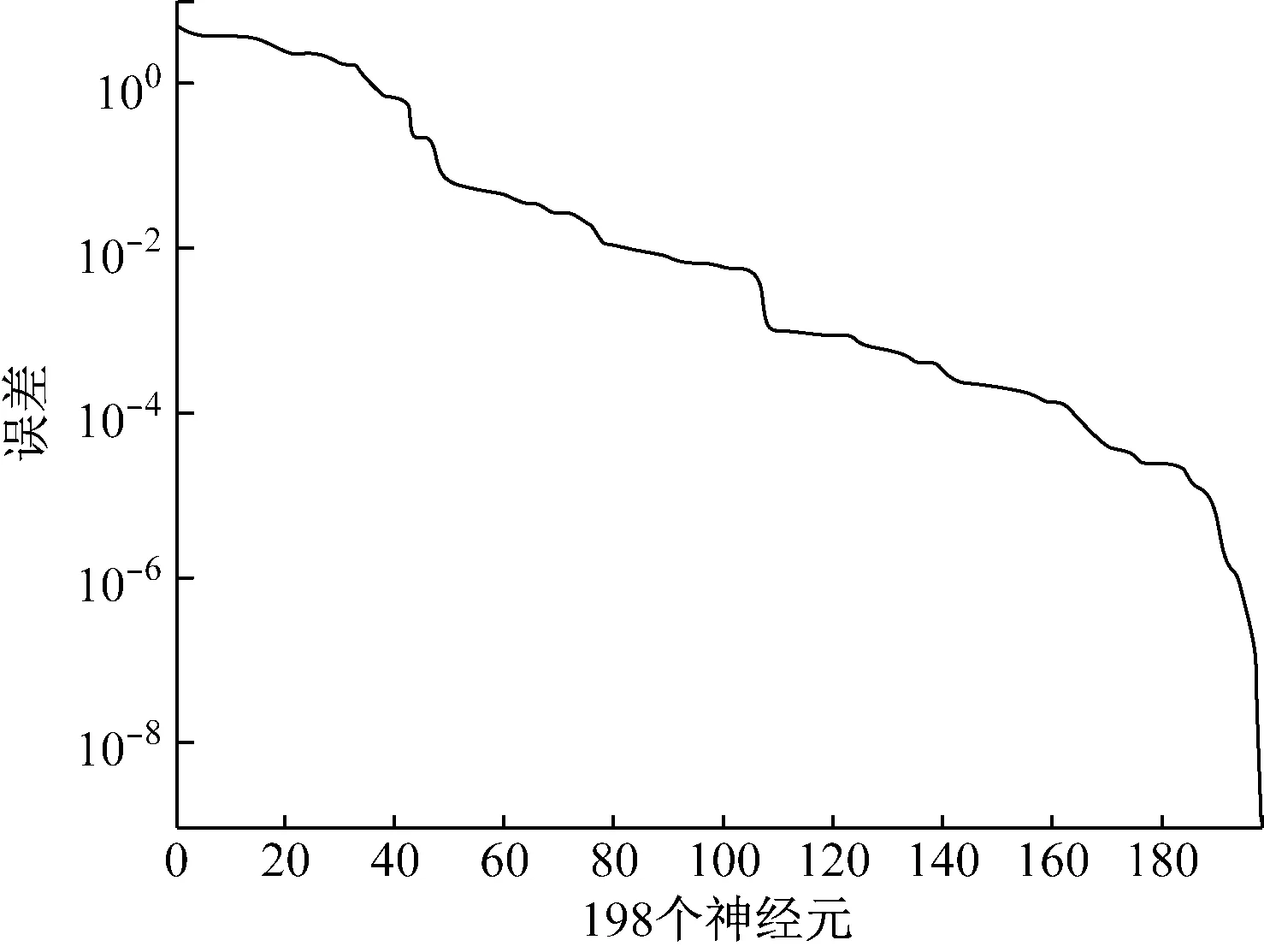
圖3 訓練誤差曲線Fig.3 Training error curve

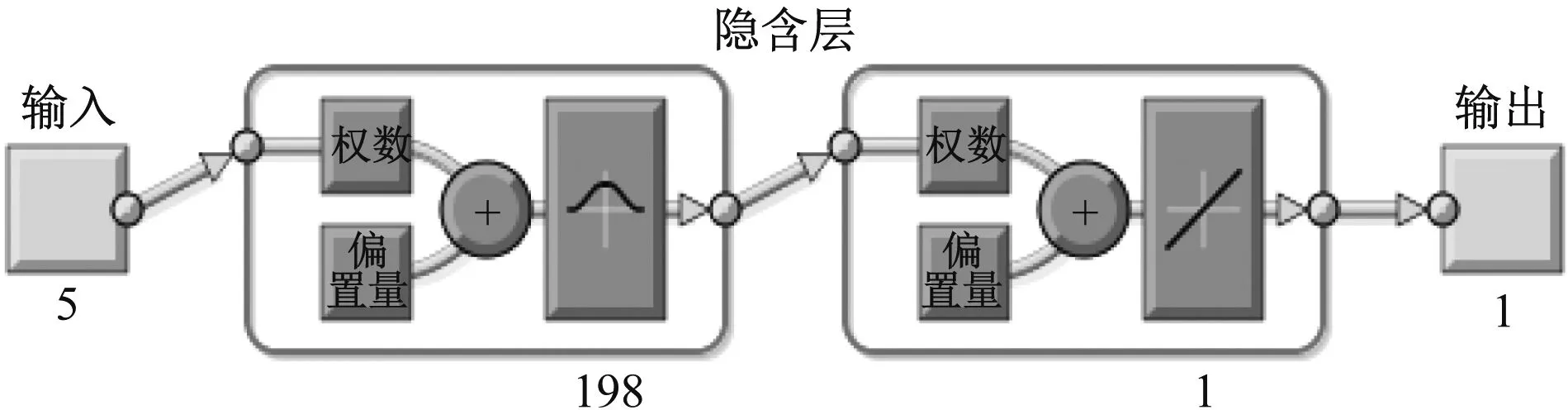
圖4 建立的RBF網絡結構圖Fig.4 Establishment of the RBF network structure

2.2預測模型驗證

為驗證模型的準確性，對選取的25個樣本進行預測，結果如圖5所示.由圖5可以看出，預測值與真實值非常接近，且兩者的變化趨勢完全一致.從相對誤差的角度來看，100份測試樣本的平均相對誤差接近0.8%，最大相對誤差接近4.8%，驗證了采用RBF神經網絡建立SCR脫硝效率預測模型的準確性，并可根據預測模型結果計算SCR系統運行成本.

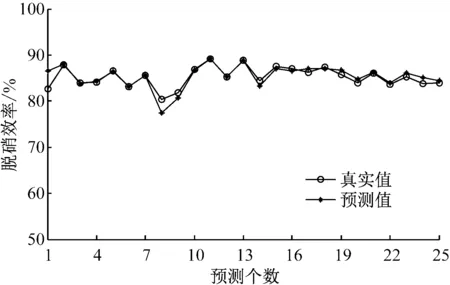
圖5 SCR脫硝效率真實值與預測值的對比Fig.5 Comparison of denitrification efficiency between actual measurements and predicted results

3 噴氨優化控制

3.1SCR系統運行成本與噴氨質量流量的關系

穩定工況下鍋爐負荷、煙氣體積流量、SCR煙氣溫度、脫硝進口NOx質量濃度均為定值，噴氨質量流量為變量，式(9)的SCR脫硝效率可認為是關于噴氨質量流量的函數，即SCR系統運行成本是關于噴氨質量流量的函數.在滿足NOx排放標準的前提下，以SCR系統運行成本最小為目標，利用Matlab對該模型進行仿真實驗，尋求氨耗成本和電耗成本與NOx排放費用的臨界點，得到最佳噴氨質量流量.

以如下工況為例計算最佳噴氨質量流量：鍋爐負荷為330.9 MW，煙氣體積流量為1 063.7 m3/h、SCR煙氣溫度為353 ℃、脫硝進口NOx質量濃度為317.3 mg/m3、噴氨質量流量為155.3 kg/h.根據建立的預測模型，SCR脫硝效率為81.6%，從而可計算SCR系統運行成本F.由于污染物排放達到標準后的電價補償以及人工、折舊、維修等費用固定，因此僅需考慮氨耗成本、電耗成本以及NOx排放費用.根據式(17)可得到F′，其中F1=3qm,a，F2=2.54qm,a-155.9，F3=816.9-4.31qm,a，則F′可表示為：

F′=(1.23qm,a+661)/P

(18)

由式(18)可以看出，SCR系統運行成本與噴氨質量流量呈正相關，因此降低噴氨質量流量，可減小SCR系統運行成本.但降低噴氨質量流量直接導致SCR脫硝效率降低，使得脫硝出口NOx質量濃度無法滿足排放標準，且面臨罰款.

3.2優化噴氨質量流量

以噴氨質量流量為自變量，以SCR系統運行成本最小為目標，同時滿足NOx排放標準，利用Matlab對該模型進行仿真實驗，計算出最佳噴氨質量流量為164.9 kg/h，優化前后SCR系統運行成本的對比如圖6所示.

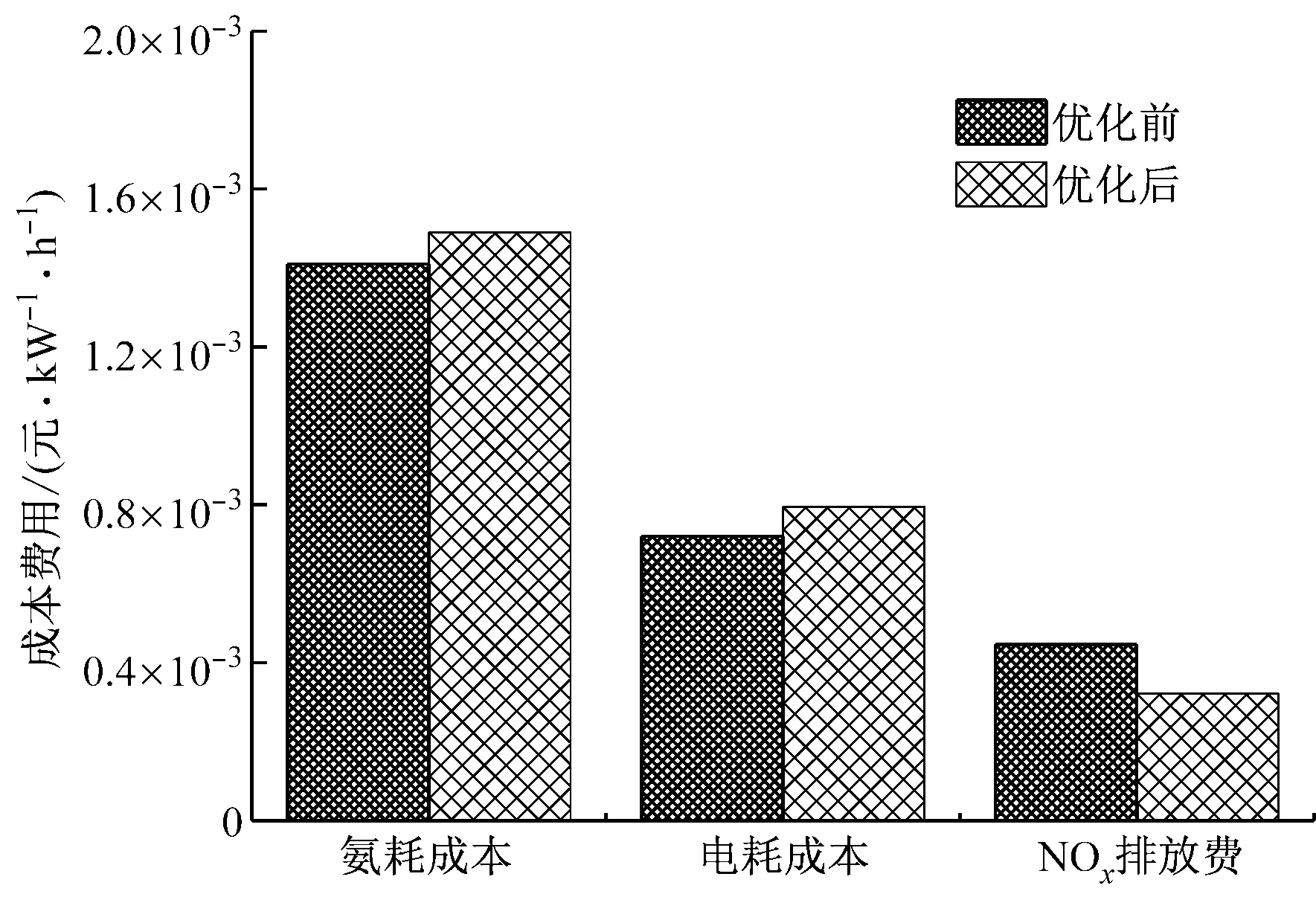
圖6 優化前后各項SCR系統運行成本對比Fig.6 Operation cost of the SCR system before and after optimization

由圖6可知，優化后氨耗成本比優化前上升了5.7%，電耗成本比優化前上升了約10.1%，而排污費用比優化前下降了約28.0%.通過對噴氨的優化控制，雖然氨耗成本和電耗成本的增加使得SCR系統運行成本F′略有上升，但NOx排放達到要求，且排污費用也會降低.

3.3不同工況下噴氨優化控制

計算不同工況下的最佳噴氨質量流量，結果如表4所示.由表4可知，8個工況下優化前后噴氨質量流量的變化有增有減，且變化幅度不一.當脫硝出口NOx質量流量不能滿足排放標準時，需增加噴氨質量流量，使NOx的脫除量增加，雖然氨耗成本及電耗成本會增加，但NOx排放量減少，可降低排污費用；當SCR脫硝效率較高，在滿足NOx排放的基礎上可適當減小噴氨質量流量，降低SCR系統運行成本.因此，在滿足排放標準的前提下，氨耗成本和電耗成本與NOx排放費用的臨界點即為最小SCR系統運行成本對應的最佳噴氨質量流量.

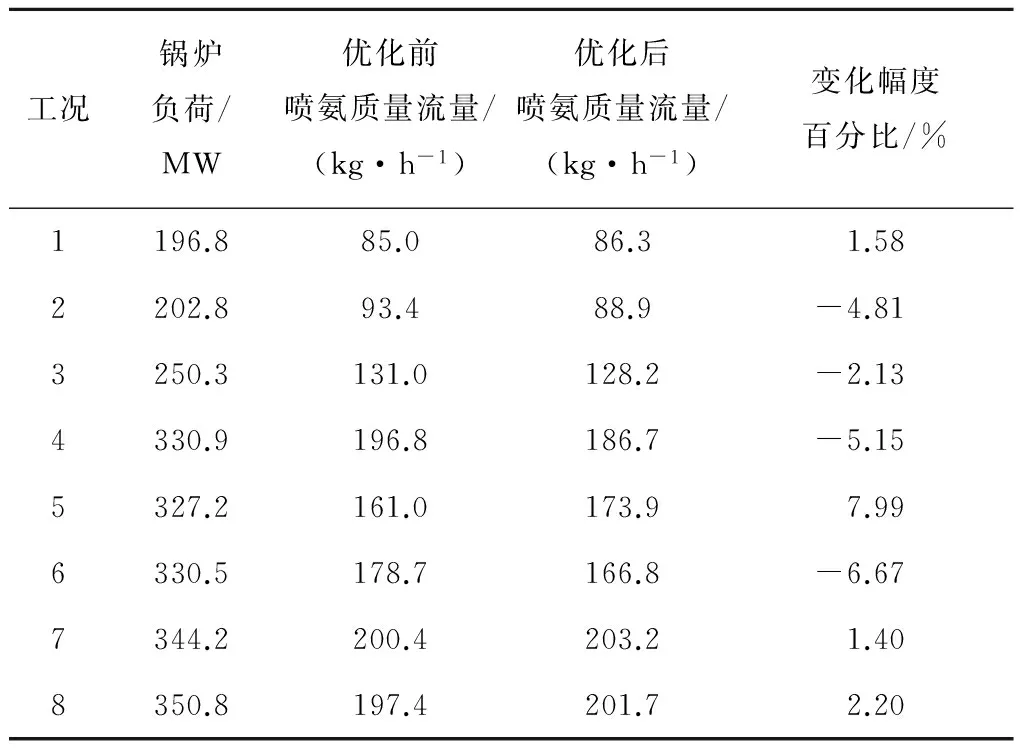
表4 不同工況下優化前后噴氨質量流量對比

4 結 論

(1)采用RBF神經網絡的方法，以鍋爐負荷、煙氣體積流量、SCR煙氣溫度、脫硝進口NOx質量濃度以及噴氨質量流量等為輸入變量，以SCR脫硝效率為輸出變量，建立SCR脫硝效率預測模型，其誤差在可接受范圍內，說明預測值是可信的.

(2)在滿足NOx排放標準的前提下，以SCR系統運行成本最小為目標，利用Matlab對該模型進行仿真實驗，尋求氨耗成本和電耗成本與NOx排放費用的臨界點，得到最佳噴氨質量流量.

(3)雖然最佳噴氨質量流量計算值比實測值或高或低，但在滿足NOx排放標準的前提下，其SCR系統運行成本的趨勢是降低的.

[1] 黃文靜, 戴蘇峰, 艾春美, 等. 電站燃煤鍋爐全負荷SCR脫硝控制技術探討[J].節能技術, 2015, 33(2): 189-192.

HUANG Wenjing, DAI Sufeng, AI Chunmei, et al. Discussion about SCR denitration control technology under full load in a coal-fired boiler[J].EnergyConservationTechnology, 2015, 33(2): 189-192.

[2] 中華人民共和國國家質量監督檢驗檢疫總局. 火電廠大氣污染物排放標準: GB 13223—2011[S]. 北京: 中國環境科學出版社, 2012.

[3] 中華人民共和國環境保護部.全面實施燃煤電廠超低排放和節能改造工作方案[R].北京：中華人民共和國環境保護部，2015.

[4] 顧衛榮, 周明吉, 馬薇. 燃煤煙氣脫硝技術的研究進展[J].化工進展, 2012, 31(9): 2084-2092.

GU Weirong, ZHOU Mingji, MA Wei. Technology status and analysis on coal-fired flue gas denitrification[J].ChemicalIndustryamp;EngineeringProgress, 2012, 31(9): 2084-2092.

[5] 秦勝, 張劍, 田莉雅. 火電廠氮氧化物控制技術探討[J].能源環境保護, 2012, 26(4): 44-47.

QIN Sheng, ZHANG Jian, TIAN Liya. The controlling measures of nitrogen oxides in thermal power plants[J].EnergyEnvironmentalProtection, 2012, 26(4): 44-47.

[6] 周洪煜, 張振華, 張軍, 等. 超臨界鍋爐煙氣脫硝噴氨量混結構-徑向基函數神經網絡最優控制[J].中國電機工程學報, 2011, 31(5): 108-113.

ZHOU Hongyi, ZHANG Zhenhua, ZHANG Jun, et al. Mixed structure-radial basis function neural network optimal control on spraying ammonia flow for supercritical boiler flue gas denitrification[J].ProceedingsoftheCSEE, 2011, 31(5): 108-113.

[7] 楊建國, 樊立安, 趙虹, 等. 提高催化劑反應效率的煙溫協調優化控制[J].中國電機工程學報, 2014, 34(14): 2244-2250.

YANG Jianguo, FAN Li'an, ZHAO Hong, et al. Coordinated optimization control of flue gas temperature for improving reaction efficiency of catalyst[J].ProceedingsoftheCSEE, 2014, 34(14): 2244-2250.

[8] 方朝君, 金理鵬, 余美玲. SCR脫硝噴氨優化與運行控制研究[J].電力科技與環保, 2015, 31(6): 39-42.

FANG Zhaojun, JIN Lipeng, YU Meiling. Research on optimization adjustment for ammonia injection and operation of SCR denitrification system in coal-fired power plant[J].ElectricPowerEnvironmentalProtection, 2015, 31(6): 39-42.

[9] 馬雙忱, 鄧悅, 吳文龍, 等. SCR脫硝過程中硫酸氫銨形成特性實驗研究[J].動力工程學報, 2016, 36(2): 143-150.

MA Shuangchen, DENG Yue, WU Wenlong, et al. Experimental research on ABS formation characteristics in SCR denitrification process[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(2): 143-150.

[10] 周洪煜, 趙乾, 張振華, 等. 煙氣脫硝噴氨量SA-RBF神經網絡最優控制[J].控制工程, 2012, 19(6): 947-951.

ZHOU Hongyi, ZHAO Qian, ZHANG Zhenhua, et al. Sensitivity analysis radial basis function neural network control on spraying ammonia flow denitrification[J].ControlEngineeringofChina, 2012, 19(6): 947-951.

[11] 羅子湛, 孟立新. 燃煤電站SCR煙氣脫硝噴氨自動控制方式優化[J].電站系統工程, 2010, 26(4): 59-60, 63.

LUO Zizhan, MENG Lixin. Ammonia flow automatic control mode optimization of SCR flue gas DeNOxfor coal-fired power plant[J].PowerSystemEngineering, 2010, 26(4): 59-60, 63.

[12] 周英貴, 金保昇. 基于非均勻入口條件的SCR氨噴射方法[J].華中科技大學學報(自然科學版), 2016, 44(4): 121-126.

ZHOU Yinggui, JIN Baosheng. Ammonia injection method for SCR based on non-uniform inlet condition[J].JournalofHuazhongUniversityofScienceandTechnology(NaturalScienceEdition), 2016, 44(4): 121-126.

[13] 趙大周, 王傳奇, 司風琪, 等. 多變截面選擇性催化還原系統噴氨方式數值模擬[J].熱力發電, 2015, 44(12): 93-97.

ZHAO Dazhou, WANG Chuanqi, SI Fengqi, et al. Optimization of ammonia injection in a SCR denitration system with multiple variable cross sections: numerical simulation[J].ThermalPowerGeneration, 2015, 44(12): 93-97.

[14] 劉曉敏. 煙氣脫硝SCR裝置噴氨優化研究[J].熱力發電, 2012, 41(7): 81-83.

LIU Xiaomin. Optimization of ammonia injection for SCR equipment[J].ThermalPowerGeneration, 2012, 41(7): 81-83.

[15] 曹志勇, 譚城軍, 李建中, 等. 燃煤鍋爐SCR煙氣脫硝系統噴氨優化調整試驗[J].中國電力, 2011, 44(11): 55-58.

CAO Zhiyong, TAN Chengjun, LI Jianzhong, et al. Experiment of optimization adjustment for ammonia injection of selective catalytic reduction flue gas denitration system in coal-fired boiler[J].ElectricPower, 2011, 44(11): 55-58.

[16] 王桂林, 張宇, 王森, 等. 基于支持向量機的選擇性催化還原脫硝系統運行優化[J].環境工程學報, 2015, 9(10): 5011-5016.

WANG Guilin, ZHANG Yu, WANG Sen, et al. Operation optimization of selective catalytic reduction system based on support vector machine[J].ChineseJournalofEnvironmentalEngineering, 2015, 9(10): 5011-5016.

[17] 宋清昆, 李源松. RBF神經網絡鍋爐燃燒系統建模[J].哈爾濱理工大學學報, 2016, 21(1): 89-92.

SONG Qingkun, LI Yuansong. Modeling of the boiler combustion system by RBF neural networks[J].JournalofHarbinUniversityofScienceandTechnology, 2016, 21(1): 89-92.

[18] 陳明. MATLAB神經網絡原理與實例精解[M]. 北京: 清華大學出版社, 2013.

[19] 郭斌, 廖宏楷, 徐程宏, 等. 我國SCR脫硝成本分析及脫硝電價政策探討[J].熱能動力工程, 2010, 25(4): 437-440.

GUO Bin, LIAO Hongkai, XU Chenghong, et al. Analysis of the SCR (selective catalytic reduction)-based denitration cost in China and exploratory study of its policies on denitration electricity price[J].JournalofEngineeringforThermalEnergyandPower, 2010, 25(4): 437-440.

[20] 霍秋寶, 田亮, 趙亮宇, 等. 火電機組不同脫硝方式下的運行費用分析[J].華北電力大學學報(自然科學版), 2012, 39(5): 87-92.

HUO Qiubao, TIAN Liang, ZHAO Liangyu, et al. Analysis of operation costs of thermal power units with different denitration methods[J].JournalofNorthChinaElectricPowerUniversity(NaturalScienceEdition), 2012, 39(5): 87-92.

AmmoniaSprayingOptimizationofanSCRDenitrificationSystemBasedonRBFNeuralNetwork

LIAOYongjin1,FANJunhui2,YANGWeijie2,JIPeng2,ZHANGJing2,FENGYongxin1

(1.Electric Power Research Institute of Guangdong Power Grid Corporation, Guangzhou 510080, China; 2. School of Energy and Power Engineering, North China Electric Power University, Baoding 071003, Hebei Province, China)

To optimize the control on ammonia spraying of the selective catalytic reduction (SCR) denitrification device in a 350 MW power boiler in Guangzhou, a relationship model was established between the input and output variables based on radial basis function (RBF) neural network by taking the boiler load, flue gas flow, SCR inlet flue gas temperature, SCR inlet NOxconcentration and the spraying ammonia flow as the input variables, and the SCR denitrification efficiency as the output variable, so as to realize the prediction of SCR denitrification efficiency and outlet NOxconcentration. Under the premise of satisfying the requirements of NOxemission and aiming at minimizing the operating cost of the SCR system, Matlab was used to perform a simulation experiment on the model to seek a critical point among the ammonia consumption cost, power consumption cost and the NOxemission fee, thus obtaining an optimal flow of spraying ammonia. Results show that the calculated mass flow of ammonia spraying is either higher or lower than the measurements, but the operating cost of the SCR system always keeps decreasing under the premise of meeting the NOxemission standard.

SCR; spraying ammonia flow; NOxemission; denitrification efficiency; cost

2016-07-06

2016-10-17

南方電網科研資助項目(K-GD2014-173)

廖永進(1971-)，男，陜西西安人，高級工程師，碩士，研究方向為鍋爐和煙氣脫硫裝置的調試、試驗及優化.

電話(Tel.):13503098453；E-mail：lyj23455@163.com.

1674-7607(2017)11-0931-07

X701

A

610.30