從類比到創新的跨越
——高中物理教學中類比思想方法的靈活應用
王 岳
(山東省東營市第一中學 山東 東營 257000)
從類比到創新的跨越
——高中物理教學中類比思想方法的靈活應用
王 岳
(山東省東營市第一中學 山東 東營 257000)
類比法又叫類比推理,是科學的研究方法之一。創新學習是適應時代發展要求的一種學習方式,是當前新課程改革倡導的學習方式之一。本文著重探討在高中物理教學活動中如何充分利用類比的思想與方法,培養學生的創新精神,有效地促進了學生的自主創新學習能力的發展。
類比法 新課程 創新 精神
類比是一種推理方法,即由熟悉的問題的結論,運用類比推理的方法,對新問題做出猜想性的結論,或由處理熟悉問題的方法聯想處理新問題的方法。廣泛地運用類比,可以開拓思路,引起聯想,形成猜想,找到解題途徑。類比是物理研究中最基本的創新形式,也是創新思維的最基本方法,通過類比法可以培養學生的創新精神。
一、通過類比法在物理學研究上的重要貢獻,激發學生的探索精神
物理學的發展告訴我們,很多關鍵時刻,科學家巧妙地運用了類比推理,提出科學假說,從而獲得巨大成功。通過對物理課程的學習,使學生感受到類比法在物理學發展進程中的重要作用,從而可以激發學生的求解與大膽探索的欲望。
例如,電磁理論的學習,讓學生知道正是科學家們對類比法巧妙應用,使得電磁學理論不斷的得以發展與完善。“電力平方反比定律”是人類建立宏偉壯觀的電磁理論大廈的第一塊基石。人們早就發現,帶電粒子之間存在著力的相互作用,如帶電的物體對棉布、毛皮或紙屑有吸附能力。18世紀英國化學家普里斯特列(Priestley)猜測,這個力應類似于兩個質點之間的萬有引力,即與距離的平方成反比,與它們的電荷量成正比。法國物理學家庫侖(Coulomb)贊同普里斯特列的這一猜想,并于1784年利用自己首創的扭秤實驗證明了兩個帶電質點之間的靜電力與它們之間的距離的平方成反比。通過與萬有引力的對比,庫侖又認為兩個帶電質點之間的靜電力與它們的電荷量的乘積成正比,后來他間接地證明了這個假定的正確。
物理學發展史的學習激發了學生的求知欲望與探索精神,一句“江山代有人才出,各領風騷數百年”更是激發了學生對未來物理學的探索欲望。
二、在物理教學中運用類比方法,可培養學生思維的創造性
在學習一些十分抽象地看不見、摸不著的物理量時,由于不易理解,我們就引導學生把能看見的且與之很相似的量來進行對照學習。
例如,學習靜電場一節內容中,由于“電場”概念比較抽象,學生往往難以理解。教學中可以先讓學生認識課本對該概念的提法,再讓學生體現該提法與舊概念中的那個概念可以進行類比理解。從而引導學生用力學中所學“重力場”類比“電場”。這樣學生就可以把新、舊知識進行類比理解,從而更好地掌握新概念。如此類比,相當于在新、舊知識間或者與學生熟悉的生活經驗中架起了一座橋梁,讓學生能夠從已掌握的舊知識或已有的生活概念中順利地接受和理解新知識,大大降低了教學難度,達到更好的教學效果。
三、引導學生應用類比方法解答物理習題,增強學生思維的靈活性和創新精神
教材在研究帶電粒子在勻強電場中的偏轉問題時,也是采用類比法將其稱為類平拋運動來處理的。因此在處理習題、分析某些問題時,我們也可以應用類比法建立模型,尋找規律,巧妙的處理看似復雜的問題或陌生的過程,往往讓人有“柳暗花明又一村”的感覺.
例如,如圖1所示,斜面長為L,傾角為θ、質量為M的斜面頂端上,有一質量為m、邊長為l的正方形小物塊由靜止開始下滑,若不計一切摩擦,求小物塊由頂端剛滑到底端過程中斜面在水平面上滑行的位移.
本題如果用常規的解法是:對M、m進行受力分析,分別求出加速度,根據它們兩者之間的力與位移的關系利用運動學公式求出。但是這樣顯然用的時間較多而且容易出錯,如果借助模型求解就方便多了,從分析可知:這是一個人船模型,利用人船模型的結論解決這道題就變得很容易了。
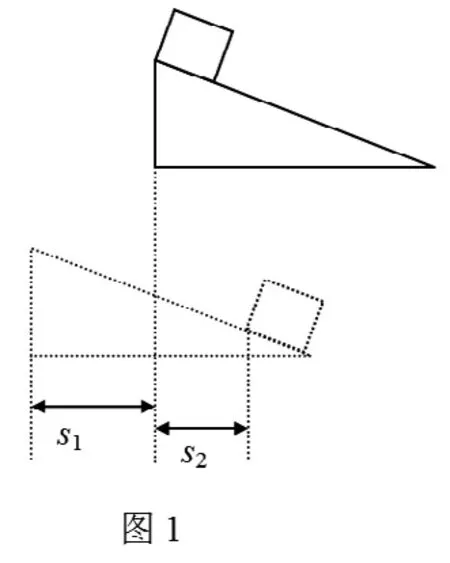
解析:設末狀態物塊和斜面對地的速度分別為v、V,以斜面的運動方向為正方向,由動量守恒得:MV-mv =0
由圖1知:S1+S2=(L-l)cosθ
可見,用類比的方法求解物理問題,可以用已知模型的物理規律求解不熟悉的物理問題,拓展了思維,也簡化了解題過程。
由此可以發現,利用類比方法得出一些新穎的解題方法,無疑對學生創新思維的培養有極大的推動作用。
四、類比法的注意問題
類比方法能使教學新穎、活躍,又能潛移默化地使學生受到物理方法教育,激發學生的探索精神。但是,類比方法是由個別到個別或一般到一般的不完全歸納推理。因為已知的相似屬性和推出的相似屬性之間不一定有必然的聯系,所以從兩個對象之間在某些屬性方面的相似或相同,并不能得出它們在某些屬性方面必然相似或相同的結論。可見,運用類比方法得出的結論不一定都是可靠的。
類比推理得到的結論的可靠程度是由相比較的兩個對象所共有的性質和推出的性質之間的聯系決定,只有類比的相同屬性多,類比屬性與類推屬性有本質聯系或聯系密切,則類比所得結論就比較可靠;否則,可靠程度就小。
因此,正確應用類比方法的關鍵是,既要選擇適當的類比對象,又要抓住事物的本質聯系作為推理的依據,同時還要在分析、綜合的基礎上比同比異,方能得到較為可靠的推論,從而實現從類比到創新的跨越。
[1]《中學物理》2009、11《理科教學探究》 方涌 陳啟平.
[2]《考試研究》2002年第3期 《物理高考“新題”的解題策略》 郁建石.
G633.7
A
2095-3089(2017)18-0097-02

