R0-代數的導子

花秀娟

西安理工大學 理學院 應用數學系，西安 710054

R0-代數的導子

花秀娟

西安理工大學 理學院 應用數學系，西安 710054

引入了代數R0-的導子并研究了R0-代數上導子的相關問題。利用導子的保序性、收縮性、不動點集和R0-代數的濾子，獲得了一個濾子成為好的理想導子濾子的充要條件，移植了不動點集在其他代數結構上的一些重要結果。

R0-代數；導子；不動點集；濾子

1 引言

為了給模糊邏輯提供更堅實的邏輯基礎，文獻[1]中提出了一種形式的演繹系統L*，并以此為背景抽象出R0-語義 Lindenbau代數的基本性質。在文獻[2]中，王國俊教授提出了R0-代數，它可以為模糊命題形式演繹系統提供一種完備性解釋[3]。

導子的理論來源于分析學，將它引入到代數系統中有助于研究代數系統的結構和性質。許多學者在不同的代數結構上研究了導子的性質[4-14]。Xin等在文獻[6]中給出了模格、分配格和具有最大元的格上的導子成為保序導子的等價條件，并利用保序導子刻畫了模格、分配格的特征。齊霄霏等文獻[8]中從幾個不同的角度給出了三角環上可加左導子的結構性質。此外，也得到了滿足一定條件的環上可加左導子的兩個不同刻畫。文獻[8]中，利用?-導子研究了BL-代數的相關性質。重點討論了BL-代數的強?-導子的性質，研究了格上的∧-導子和BL-代數?-導子的關系，并借助保序導子刻畫了BL-代數的特征。

本文給出了R0-代數導子的概念，并研究了它的一些基本性質。 而且借助理想導子刻畫了R0-代數的特征。

2 預備知識

定義2.1[1]設(M ,∨,∧,0,1)是有界分配格，':M→M是逆序對合對應，→:M→M是二元運算。M稱為R0-代數，若以下條件成立：

(M1)x′→ y′=y′→ x′；

(M2)1→x=x,x→x=1；

(M3)y→z≤(x→y)→(x→z)；

(M4)x→(y→z)=y→(x→z)；

(M5)x→(y∨z)=(x→y)∨(x→z)，

x→(y∧z)=(x→y)∧(x→z)；

(M6)(x→y)∨((x→y)→x′∨y)=1。

在R0-代數M 中，對任意x,y∈M ，定義x?y=(x→y′)′，x⊕y=x′→y 。稱 B(M)={x ∈M,x?x=x}為 M 的布爾中心。 在以下，對任意 n＞1，令 xn=

定義2.2[4]設M 是R0-代數，F?M。若x,y∈M，有

（F1）1∈F

（F2）x∈F，x→y∈F?y∈F

則稱F為M上的一個濾子。濾子的全體記為F(M)。

設 A∈M ，由 A生成的濾子(A]=?F∈F(M),A?M。

若A有限，則稱(A]是有限生成的濾子。

定 理 2.3[4](A]={x|?a1,a2,…,an∈A,v.t.a1→(…(an→x)…)=1,n∈N}

引理2.4[2]設 M 是R0-代數，則以下結論成立：?x,y,z∈M

（1）x≤y?x→y=1

（2）x≤y→x

（3） x′=x→0

（4）(x→y)∨(y→x)=1

（5）若 x≤y，則 x→z≥y→z

（6）若 x≤y，則 z→x≤z→y

（7）((x→y)→y)→y=x→y

（8）x∨y=((x→y)→y)∧((y→x)→x)

（9）x?x′=0,x⊕x′=1

（10）x?y≤x∧y,x?(x→y)≤x∧y

（11）(x?y)→z=x→(y→z)

（12）x≤y→(x?y)

（13）x?y≤z?x≤y→z

（14）若 x≤y，則 x?z≤y?z

（15）x→y≤(y→z)→(x→z)

（16）(x→y)?(y→z)≤x→z

引理2.5設M是R0-代數，則以下結論成立：?x,y,z∈M

（1）x?(y∧z)=(x?y)∧(x?z)

（2）x?(y∨z)=(x?y)∨(x?z)

證明（1）由上面的定義可知

x?(y∧z)=[x→(y∧z)′]′又由(M5)和格的性質得：

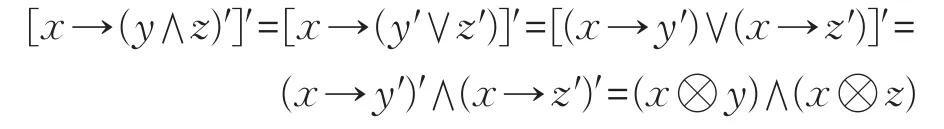
（2）同理可證。

引理2.6設 M 是 R0-代數，對任意的 x∈M ，a∈B(M)，有 x?a=x∧a。

證明 由引理2.3（1）和a∈B(M)可知，a?(a∧x)=(a?a)∧(a?x)=a∧(a??x)，因此結論成立。

3 R0-代數的導子

定義3.1設M是一個R0-代數，若d滿足：?x,y∈M ，d(x?y)=(d(x)?y)∨(x?d(y))，則稱 d 是 M 的導子。簡記d(x)=dx。

注 導子概念源于分析理論，它是對R0-代數中的元素定義的一個映射。在R0-代數中引入它，主要是為了研究R0-代數的結構和性質。

例3.2設 M 是R0-代數，對任意 x∈M ，定義一個映射d:M→M 為d(x)=0，則d是M上的導子，稱為零導子。更進一步，對任意 x∈M，定義一個映射d:M→M為d(x)=x，則d是M上的導子，稱為單位導子。

命題3.4設M是R0-代數且d是M上的導子，則下列結論成立：?x,y∈M

（1） d0=0

（2） dx?x′=0，dx′?x=0

（3） dx≥x?d1

（4） d(xn)=xn-1?dx

證明 （1）d0=d(0?0)=(d0?0)∨(0?d0)=0?d0=(0 → (d0)′)′=(d0 → 1)′=0 。

（2）0=d0=d(x?x′)=(x?dx′)∨(x′?dx)，則 x?dx′=0,x′?dx=0 。

（3）因為 dx=d(x?1)=(dx?1)∨(d1?x)=dx∨(d1?x)，所以dx≥x?d1。

（4）dx2=d(x?x)=dx?x，dx3=d(x2?x)=(dx2?x)?(x2?dx)=dx?x2，依 次 類 推 ，d(xn)=xn-1? dx成立。

定義3.5設M是R0-代數且d是M上的導子。

（1）若對任意 x,y∈M ，當 x≤y時，有dx≤dy，則稱是d保序導子。

（2）若對任意x∈M，有dx≤x，則稱d是收縮導子。

特別的，若d是保序的和收縮的，稱其為理想導子。

命題3.6設M是R0-代數且d是M上的保序導子，則下列結論成立：?x,y,z∈M

（1）若 x≤y→z，y≤dx→dz且 x≤dy→dz。

（2）x→y≤dx→dy,d(x→y)≤x→dy。

證明（1）對 ?x,y,z∈M ，若 x≤y→z，則由引理2.4（13）知 x?y≤z，因為d是保序導子，則d(x?y)≤dz，即 (dx?y)∨(x?dy)≤dz，故有 dx?y≤dz且x?dy≤dz，從而有 y≤dx→dz且x≤dy→dz。

（2）對?x,y∈M ，由引理2.4（10）知 x?(x→y)≤y，則 d(x?(x→y))≤dy ，即 (dx?(x→y))∨(x?d(x→y))≤dy。這意味著dx?(x→y)≤dy且x?d(x→y)≤dy。因而有 x→y≤dx→dy且d(x→y)≤x→dy。

命題3.7設M是R0-代數且d是M上的收縮導子，則下列結論成立：?x,y∈M

（1）dx?dy≤d(x?y)≤dx∨dy。

（2）若d是保的，d(x→y)≤dx→dy≤dx→y。

（3）(dx)n≤d(xn)。

（4）若d1=1，則d是單位導子。

證明（1）因為d是收縮導子，所以對任意x,y∈M，有 dx≤x。又由引理2.4（14）有，dx?dy≤x?dy且dx?dy≤dx?y，因而有 dx?dy≤(x?dy)∨(dx?y)=d(x?y)。另一方面，dx?y≤dx且 x?dy≤dy，從而有 d(x?y)≤(dx?y)∨(x?dy)≤dx∨dy。故有dx?dy≤d(x?y)≤dx∨dy。

（2）由引理2.4（10），對任意 x,y∈M ，x?(x→y)≤y，可得 d(x?(x→y))≤dy。由（1）知，dx?d(x→y))≤d(x?(x→y))，從而有dx?d(x→y)≤dy，即 d(x→y)≤dx→dy 。另一方面，由引理 2.4（6）當x≤y時，dx→dy≤dx→y。從而有 d(x→y)≤dx→dy≤dx→y。

（3）由（1）知 dx?dx≤d(x?x)，故 dx?dx?dx≤d(x?x)?dx≤d(x?x?x)。依此類推，(dx)n≤d(xn)。

（4）由命題3.4（3）知 dx≥x?d1，假設 d1=1，可得x=x?1≤dx≤x。故對任意x∈M ，dx=x。即d是單位導子。

定理3.8設M是R0-代數且d是M上的導子，則下面是等價的：

（1）設d是 M 的理想導子且d2=d，其中對任意x∈M ，d2(x)=d(dx)。

（2）對任意 x,y∈M ，d滿足dx→dy=dx→y。

證明 (1)?(2)假設d是M 的理想導子且d2=d。對任意 y∈M ，由dy≤y得dx→dy≤dx→y。 另一方面，令t≤dx→y，其中t∈M ，則dx?t≤y。因為d是保序的，所以 d(dx?t)≤dy。由 d(x?y)≤(dx?y)∨(x?dy)，可得d(x?y)≤dx?y。從而d(dx?t)≥d(dx)?t，又 d2=d ，所以 dx?t≥d(dx?t)≤dy。故t≤dx→dy，這意味著dx→y≤dx→dy。因而對任意 x,y∈M ，dx→dy=dx→dy。

(2)?(1)假設對任意 x,y∈M ，dx→dy=dx→y。首先，因為dx?1≤dx，所以1≤dx→dx=dx→x，則dx?1≤dx，即dx≤x。因而d是收縮導子。更進一步，對任意 x,y∈M ，設 x≤y，有dx?1=dx≤x≤y，得到1≤dx→y=dx→dy，這意味著 dx?1≤dy，即dx≤dy。因而d是保序。 故d是M的理想導子。最后，因為dx?1≤dx，所以1≤dx→dx=dx→d(dx)。則 dx?1≤d(dx)，得出 dx≤d(dx)，結合 d(dx)≤dx，有d(dx)=dx，即d2=d。

定理3.9設M是R0-代數且d是M上的收縮導子，若d1∈B(M)，則下面結論是等價的：

（1）d是理想導子；

（2）dx≤d1；

（3）dx=d1?x；

（4）d(x∧y)=dx∧dy；

（5）d(x∨y)=dx∨dy；

（6）d(x?y)=dx?dy。

證明 (1)?(2)因為對任意 x∈M ，x≤1，且d是單調的，故有dx≤d1。

(2)?(3)假設對任意x∈M ，有dx≤d1。因為d1∈B(M)，所以 dx=d1∧dx=d1?dx≤d1?x ，另一方面，由命題 3.4（3）可知 dx≥x?d1，因而有 dx=d1?x。

(3)?(4)假設對任意x∈M ，dx=d1?x。即d(x∧y)=d1?(x∧y)=d1∧(x∧y)=(d1∧x)∧(d1∧y)=(d1?x)∧(d1?y)=dx∧dy。

(4)?(1)假設 x≤y，則 x∧y=x。由（4）可知 dx=d(x∧y)=dx∧dy，即dx≤dy。所以d是理想導子。

(3)?(5)由引理 2.4（2）和（3）可知 d(x∨y)=d1?(x∨y)=(d1?x)∨(dx?y)=x∨y。

(5)?(1)假設 x≤y，則 x∨y=y。由（5）可知 dy=d(x∨y)=dx∨dy，即dx≤dy。 所以d是理想導子。

(3)?(6)由（3）可知 d(x?y)=d1?(x?y)=(d1?x)?(d1?y)=dx?dy。

(6)?(2)dx=d(x?1)=dx?d1=dx∧d1，即dx≤d1。

命題3.10設M 是R0-代數且d，d1，d2是M上的理想導子，則有

（1）對?x,y∈Fixd(M)，x?y,x∨y∈Fixd(M)。

（2）若d1∈B(M)，則d1=d2當且僅當

Fixd1(M)=Fixd2(M)

證明（1）對任意x,y∈Fixd(M)，有dx=x且dy=y。由命題3.7（1）可得 x?y=dx?dy≤d(x?y)≤x?y，這意味著 x?y∈Fixd(M)。另一方面，d是 M 上的理想導子，所以 x∨y=dx∨dy≤d(x∨y)≤x∨y，由此可得d(x∨y)=x∨y，即 x∨y∈Fixd(M)。

（2）設 d1=d2，很顯然 Fixd1(M)=Fixd2(M)。反之，假設 Fixd1(M)=Fixd2(M)，因為 d11∈B(M)，所以由定理3.9（3）可知對任意 x∈M ，d1x=d11?x，進而d1(d1x)=d11?d1x=d11?(d11?x)=d11?x=d1x，即 d1(d1x)=d1x，故 d1x∈Fixd1(M)=Fixd2(M)，因而d2(d1x)=d1x。同理可得d1(d2x)=d2x。另一方面，d1，d2是M 上的理想導子，有d1(d2x)≤d1x=d2(d1x)。即d1(d2x)≤d2(d1x)。用同樣的方式可得d2(d1x)≤d1(d2x)。故d1(d2x)=d2(d1x)，從而d2x=d1(d2x)=d2(d1x)=d1x。

定義3.11設M是R0-代數，d是M上的一個理想導子且F是M 的濾子，對任意 x∈M ，若 x∈F推出dx∈F，則稱F是M的理想導子濾子。

命題3.12設M是R0-代數，d是M上的理想導子。 若F是M的濾子，則F是M的理想導子濾子的充要條件是F=(F?Fixd(M)]。

證明 設F是M的理想導子濾子。設x∈F，則dx∈F 。又由定理 3.8（1）可知 dx∈Fixd(M)，得到dx∈(F?Fixd(M)]。由dx≤x可得x∈(F? Fixd(M)]。從而F?(F?Fixd(M)]。另一方面，設x∈(F?Fixd(M)]，則存在 y∈(F?Fixd(M)]使得 x≥y。因此有 x≥dx≥dy=y，故 x∈F。所以F=(F?Fixd(M)]。

反之，假設F=(F?Fixd(M)]。設x∈F，x→dx∈F，由定理2.3可知存在 a1,a2,…,am∈F?Fixd(M)，b1,b2,…,bn∈F?Fixd(M)使得 a1→(…(am→x)…)=1，b1→(…(bn→(x→dx))…)=1 ，由定義 3.1（M4）得 x→(b1→(…(bn→dx))…)=1 ，即 x≤b1→(… (bn→ dx)…)。所以 1=a1→(… (am→x)…)≤ a1→(… (am→ (b1→(…(bn→dx))…))…)，因 此 a1→(… (am→(b1→(…(bn→dx))…))…)=1，即 dx∈F 。

4 結束語

本文將導子理論應用到R0-代數上，引入R0-的導子的概念并給出例子。利用導子的保序性、收縮性、不動點集和R0-代數的濾子，獲得了一個濾子成為好的理想導子濾子的充要條件，移植了不動點集在其他代數結構上的一些重要結果。由于導子理論可以更好地研究代數系統的結構和性質，因而還可以進一步研究基本代數的導子。

[1]王國俊.模糊命題演算的一種形式[J].科學通報，1997，42（10）：1041-1045.

[2]王國俊.非經典數理邏輯與近似推理[M].北京：科學出版社，2000.

[3]裴道武，王國俊.邏輯系統?的完備[J].中國科學：E輯，2002，1：56-64.

[4]程國勝.R0代數中的濾子與理想[J].模糊系統數學，2001，15（1）：58-61.

[5]Posher E.Derivations in prime rings[J].Proceedings of the American Mathematical Society，1957，8（6）：1093-1100.

[6]Xin X L，Li T Y，Lu J H.On derivations of lattice[J].Information Science，2008，178（2）：307-316.

[7]Alshehri N O.Derivations of MV-algebras[J].International Journal of Mathematics and Mathematical Sciences，2010（10）：932-937.

[8]齊霄霏，鞏琳.環上可加導子的刻畫[J].數學學報，2015，8（6）：1021-1034.

[9]辛小龍，馮敏，楊永偉.BL-代數上的⊙-導子[J/OL].數學雜志，2015.http：///www.cnki.net/kcms/doi/10.13548/j.sx22.2013102100/html.

[10]花秀娟，朱熙.格效應代數的微分[J].模糊系統數學，2015，29（3）：114-118.

[11]程國勝，王國俊.R0代數及其基本結構[J].數學物理學報，1999，19（5）：584-588.

[12]Asokkumar A.Derivations in hyperring and prime hyperring[J].Iranian Journal of Mathematical Science and Informatics，2013（8）：1-13.

[13]Zhan J，Liu Y L.On f-derivations of BCI-algebras[J].International Journal of Mathematics and Mathematical Sciences，2005，25（11）：1675-1684.

[14]Jun Y B，Xin X L.On derivations of BCI-algebras[J].Information Sciences，2004，159（3/4）：167-176.

HUA Xiujuan

Department of Mathematics,Xi’an University of Technology,Xi’an 710054,China

On derivations of R0-algebra.Computer Engineering and Applications,2017,53（21）：54-57.

In the paper,the derivation ofR0-algebra is introduced and investigated.By using the isotone property,contractive property,fixed point sets and filters ofR0-algebra,the necessary and sufficient condition of a filter to be a good ideal derivation filter is obtained.Some important results of fixed point sets on other algebra structure is popularized.

R0-algebra;derivations;fixed point sets;filters

A

O141.1

10.3778/j.issn.1002-8331.1606-0343

陜西省西安理工大學科學研究計劃項目（No.2015CX009）。

花秀娟（1981—），女，博士，講師，研究領域為模糊代數，不確定性理論，E-mail：huaxiujuan1028@163.com。

2016-06-24

2016-08-30

1002-8331（2017）21-0054-04

CNKI網絡優先出版：2016-12-21,http://www.cnki.net/kcms/detail/11.2127.TP.20161221.0842.022.html