雙目標優化的RDF圖分割算法

陳志奎 ，冷泳林 ，2

1.大連理工大學 軟件學院，遼寧 大連 116620 2.渤海大學 信息科學與技術學院，遼寧 錦州 121000

雙目標優化的RDF圖分割算法

陳志奎1，冷泳林1，2

1.大連理工大學 軟件學院，遼寧 大連 116620 2.渤海大學 信息科學與技術學院，遼寧 錦州 121000

分布式存儲是解決大規模數據存儲的一種比較有效的方法，而數據分割是實現分布式存儲的前提。面對不斷增長的RDF數據，提出一種基于雙目標優化的RDF圖分割算法（RDF Graph Partitioning algorithm based on Double Objective Optimization，RGPDOO）。RGPDOO將邊割和分割平衡兩項圖分割指標融合到一個目標函數，并依據此目標函數，實現了RDF圖的靜態和動態分割。其中靜態圖分割通過對圖進行初始劃分，將圖中頂點分成內核頂點、交叉頂點和自由頂點三類。然后通過計算目標函數增益對交叉和自由頂點進行分配。動態圖分割部分，針對RDF元組的插入和刪除給出相應的解決方案。同時，為了滿足圖分割目標，算法每隔一段時間T會根據子圖的平衡性和緊密性進行一次動態調整。實驗選擇合成和真實數據集進行測試，并分別與幾種通用的靜態和動態圖分割算法進行比較。實驗結果表明提出的算法能夠有效地實現RDF圖的靜態和動態分割。

RDF圖；靜態分割；動態分割；邊割；負載均衡

1 引言

萬維網聯盟（W3C）推薦的資源描述框架（Resource Description Framework，RDF）是描述語義網中各種資源與它們之間語義關系的一個重要框架標準[1]。RDF使用三元組〈主語，謂語，賓語＞來描述世界，當把主語和賓語看做圖中兩個頂點，謂語看做是由主語指向謂語的有向邊時，RDF數據集可以被看做是一個有向圖。隨著Link Open Data（LOD）[2]和DBpedia等項目的全面展開，語義Web的數據量不斷增加，大量RDF數據被發布。

面對大規模RDF數據，傳統單機模式已經不能滿足數據存儲需求。數據分布式存儲是目前公認地解決大規模數據存儲比較有效的方法。而實現分布式存儲的前提就是如何有效對數據進行分割。尤其是RDF圖本質特征，使數據之間存在大量關聯。如果分割不當，就會導致查詢時，存儲節點之間產生大量通信。另外，分割平衡性也將影響數據并行執行的效率。并且，RDF數據是不斷更新變化的，要保持良好的分割狀態，對應的數據分割算法就應該具有適應數據變化的能力。

基于以上分析，本文提出一種雙目標優化的RDF圖分割算法（RDF Graph Partitioning algorithm based on Double Objective Optimization，RGPDOO）。算法以最小化邊割和分割平衡作為RDF圖分割目標設計了一個雙目標優化函數。并基于此目標函數實現了RDF數據的靜態和動態圖分割算法。實驗中，本文選擇RDF標準數據集從邊割、分割效率和分割平衡三方面驗證算法的有效性。實驗結果表明，本文提出的雙目標函數從邊割和平衡兩方面保證RDF圖數據分割的質量，有效地實現RDF圖的靜態和動態分割。

文中其他部分內容概括如下：第2章介紹RDF圖分割相關工作；第3章詳細闡述雙目標函數的設計；第4章描述了雙目標函數下RDF圖的靜態和動態分割算法；最后通過實驗驗證RGPDOO算法的性能并得出結論。

2 相關工作

近年來，隨著RDF數據的廣泛應用，關于RDF圖分割算法的研究也越來越多。SPA[3]采用頂點中心塊兒的分割機制對RDF圖進行分割。VB-Partitioner[4]擴展了SPA思想，在其基礎上對頂點中心塊兒進行n跳擴展，來避免查詢時節點間的通信。BRGP專門針對RDF圖中頂點的不對稱關系以及圖的冪率特性提出基于模塊度的標簽傳播算法對圖進行粗化分割。Wu[5]等人提出了一種基于路徑的圖分割算法，算法將RDF圖分解成由源點到匯點所組成的路徑，然后再以路徑為單位進行分割。Huang等人將METIS圖分割框架直接應用于RDF數據分割，通過副本方式降低SPARQL查詢中各分區之間的通信[6]。Wang等人利用標簽傳播算法對RDF圖頂點進行粗化，并結合METIS對粗化圖進行分割[7]。以上這些算法都是基于靜態RDF圖進行分割，并沒有給出圖動態變化時的解決方案。

朱牧等人提出基于密度的增量聚類算法可以實現圖的增量分割，但該算法主要傾向于社交網絡中重疊社區發現問題，并沒有考慮圖分割的邊割和平衡兩項分割指標[8]。Fennel是一種基于流的圖分割框架，該框架在目標函數地限制下結合一定的啟發式算法來實現圖分割[9]。張曉媛[10]等人提出的基于鄰域動態圖分割算法NDA在靜態圖分割的基礎上，按照不同的圖數據增長方式，根據存儲節點最小負載原則或KNN原則進行節點的遷移或添加。該算法在動態圖分配階段只考慮負載均衡來轉移不平衡節點，并沒有考慮邊割問題。Martella[11]等人提出的Spinner是一種基于標簽傳播的增量圖分割算法，Spinner在Pregel分布式圖計算平臺基礎上將標簽傳播算法擴展成為一種分布式的圖分割算法，保證分割算法的可擴展性。Spinner能夠根據圖和計算環境的變化自動調整圖分割結果，避免圖的重新分割。在處理增量節點時，Spinner通過重啟迭代的方式，讓全局頂點都參與到最優計算中，雖然獲得了一個很好的分割結果，但這種方式非常耗時。SPAR[12]以最小化副本為分割目標將社交網絡中每個用戶所有相關信息劃分到一個存儲節點來保證分割局部語義完整性。并且針對節點、邊和存儲節點的添加刪除給出了圖的自適應分割策略。Sedge[13]提出了補充和按需兩種分割技術，并依據這兩種技術，創建了一個具有兩層分割結構的圖分割架構：主要分割和輔助分割，來處理變化的圖查詢。Xu等人提出的LogGP[14]將圖和歷史分割結構結合到一起，構成一個超圖，并且利用基于超圖的流分割方法得到初始分割。在分割過程中，還會依據運行時的統計信息評估每個節點的運行時間，對后繼執行做出動態調整。以上這些算法在圖的動態分割方面做出了貢獻，但這些算法并沒有針對RDF圖特征及其分割目標給出合適的解決方案。

3 雙目標優化函數的設定

給定一個RDF圖G=(V,E)，其中V表示圖中頂點集合，E表示圖中的邊集，|V|=n和|E|=m分別表示圖中頂點和邊的數目。一個k路圖分割就是將RDF圖分成 k個不相連接的子圖 P={G1,G2,…,Gk}，其中Gi={Vi,Ei},i=1,2,…,k是一個分割子圖。當 i≠j時，Vi∩Vj=φ并且

邊割和平衡性是衡量圖分割質量的兩項重要指標，其中邊割是指連接兩個不同子圖之間邊。子圖之間邊割越小，表示它們之間的聯系越稀疏，數據并行執行時彼此之間需要交換的信息越少，數據并行性越高。本文用inter(Gi,Gj)表示子圖Gi和Gj之間的邊割，則：

當來自兩個不同子圖的頂點a和b之間存在連接，則e(a,b)為1，否則為0。同邊割相對應，用intra(Gi)表示任意一個子圖內部邊的數目，本文定義為內割，則：

顯然，一個子圖的內割越高，子圖內部節點之間關系越緊密，即子圖獨立性越強。

圖分割的平衡性是指各分割子圖中頂點的數目趨于相等。在分布式系統中各存儲節點硬件環境相同情況下，各子圖頂點規模越趨于相等，系統并行執行的效率越高。當任意一個分割子圖Gi中頂點數目滿足公式（3）時，圖分割P趨于平衡。其中e是一個介于0和1之間的浮動因子，即允許圖規模在一定范圍內浮動。

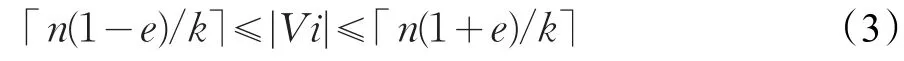
由以上分析，圖分割不僅要最小化邊割，而且還要保證分割子圖的平衡性。為此，本文提出一個基于邊割和平衡的雙目標函數 f(P),f(P)滿足：

其中cut(P)代表圖分割的邊割，對于一個k路圖分割P，cut(P)滿足：

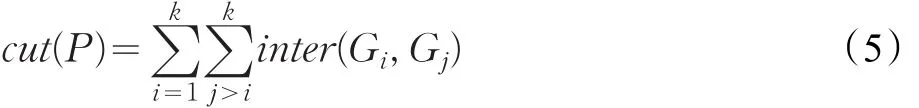
其中：

balance(P)代表圖分割的平衡性，balance(P)滿足：

綜上，當雙目標函數 f(P)取最小值時，圖分割結果最優。但圖分割是一個NP-完全問題，要得到精確分割結果是很困難的。因此目標是尋找一個近似最優解。為實現這一目標，對 f(P)做如下處理。

給定一個函數g(P)，如公式（8）所示：

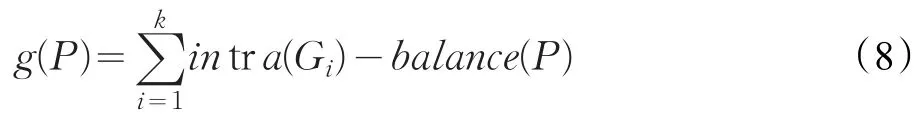
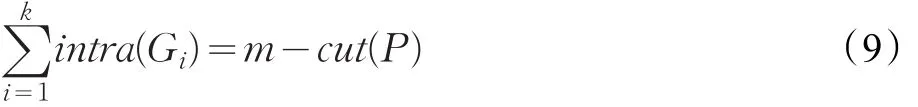
由公式（4）、（8）和（9）可得：

當求 f(P)的最小值時，對應就是求g(P)的最大值。因此，在確定一個頂點v所屬分區時，可以通過計算?g(P,i,v)的最大增益值來確定。

如圖1，設n/k=4，兩個分割子圖G1和G2的 g(p)當前值為7。當新節點i分別加入到子圖G1和G2時，g(p)的值為7和8，則產生的增益值分別為?g(P ,G1,i)=1和?g(P ,G2,i)=0，因此選擇G2分區。從圖1中也可以直觀看出，加入G2所產生的邊割要小于G1，而平衡性的變化是一致的。

圖1 計算最大增益值

4 基于雙目標函數的RDF圖分割算法

基于以上目標函數，本章給出兩種不同狀態RDF圖分割算法。第一種是針對已經存在的靜態RDF圖，另一種是針對變化的RDF圖給出的動態分割方案。

4.1 靜態圖分割

本文基于雙目標函數，改進了k路貪婪圖分割算法（Improved k-way Greedy Graph Growing Partitioning，IKGGGP）[15]，實現了對靜態RDF圖的分割。不同于KGGGP算法，IKGGGP算法首先對RDF圖進行初始劃分，將圖中頂點劃分成只屬于一個分區的內核頂點；存在于多個分區的交叉頂點和不屬于任何分區的自由頂點。對于內核頂點，它們只屬于一個唯一分區，無需再進行分配。而交叉頂點和自由頂點，IKGGGP通過計算目標函數的最大增益值為它們選擇合適分區。

4.1.1 初始劃分

SPARQL查詢本質是子圖匹配問題，如果將緊密聯系的節點分配到同一分區，將極大地降低查詢時存儲節點之間的通信。當圖中頂點同其鄰域具有很大相似性時，這個頂點更容易成為圖中的一個核心頂點。本文就從圖中的k個核心頂點開始向外擴展，對RDF圖進行初始劃分。經過初始劃分的圖中存在一類特殊頂點，它們是只與分區內的頂點有關聯的內核頂點。如圖2所示的紅色頂點即是內核頂點。內核頂點只屬于一個分區，因此一旦初始區域劃分結束，這些頂點的分區也就固定，不需要在進行分區選擇。

給定一個RDF圖，Γ(v)是頂點v的鄰域集合。Γε(v)表示頂點v的鄰域中與v的相似度大于或等于閾值ε的頂點集合。如果|Gε(v)|的鄰域數目超過閾值δ，稱頂點v是圖中的一個核心頂點。

在尋找RDF圖中核心頂點時需要計算頂點v與其鄰域頂點的相似性。傳統地計算圖節點相似性的方法都是基于頂點的結構信息，如隨機游走[16]、計算公共鄰域[17]等方法。本文由于RDF圖是一個語義圖，節點間存在一定的語義關系。如果將語義上聯系緊密的頂點劃分到一個分區，將更有利于查詢的并行執行。因此本文提出了一種基于語義的頂點相似性度量方法。

RDF采用統一資源標識符（Uniform Resource Identifier，URI）來標識圖中的頂點和邊。URI通過目錄結構體現圖中頂點所屬類、超類及節點信息。如果圖中兩個頂點所屬公共超類越多，說明它們的相似性就越大，即這兩個頂點聯系越緊密。用函數sup(v)來計算頂點v所屬超類，則衡量兩個頂點u和v的語義相似性，如公式（11）所示：

當某一個頂點只有一個入邊，則它與指向它的頂點的相似性為1。當確定圖中核心點后，就可以對圖進行初始劃分了。算法1給出了初始劃分的偽代碼。

算法1初始劃分

輸入 核心頂點集core,圖G

輸出 初始劃分P={G1,G2,…,Gk}

方法：

Initialqueue(q)；p＜—1；//初始化隊列q和分區編號

Do while p＜=k

v〈—select(core)；//從核心頂點集隨機選擇一個頂點

remove(core,v)；//從核心頂點集移除v

inqueue(q,v)；//頂點v入隊列

i＜—1；

partition(v)＜—p；//為頂點分配分區編號和分區內序號

number(v)＜—i；

i＜—i+1；Gp=Gp?v；

Do while not isempty(q)andi＜n/k

v＜—outqueue(q)；

for each u in Γε(v)do

ifu∈core

remove(core,u)；

ifu?Gp

inqueue(q,u)；

partition(u)＜—p；

number(u)＜—i；

ifi=n/k

exit for

i＜—i+1；Gp=Gp?u；

end for

end do

p=p+1；

clearqueue(q)；//清空隊列

end do

4.1.2 交叉頂點和自由頂點分配

當RDF圖經過初始分割后，內核頂點的分區已經確定。除了內核頂點，初始分割結果中還存在兩類頂點，如圖2中紫色的交叉頂點和藍色的自由頂點（統稱為待分配節點），需要計算它們所屬分區。本文通過計算函數g(P)的最大增益值，來確定這兩類頂點的分區，即：

圖2 RDF圖分區的核心頂點

IKGGGP算法中待分配頂點分配執行步驟如下：

步驟1計算所有待分配頂點分配到各個分區所產生的增益值Δg。

步驟2選擇產生最大增益的頂點v和其對應的分區i，將其分配到分區i，從待分配頂點集合移除v。

步驟3如果待分配頂點集合不為空，更新其他待分配頂點的增益值Δg，返回步驟1，否則，執行步驟4。

步驟4輸出分區結果。

為提高算法效率，本文對以上執行步驟做了如下兩方面處理：

（1）設計一個二維數組存儲待分配頂點分配到不同分區產生的增益值?g，其中二維數組中的每一行對應一個待分配頂點，每一列對應一個分區。當將一個頂點v分配到分區i后，其他待分配頂點在各個分區增益變化遵循公式（13）：

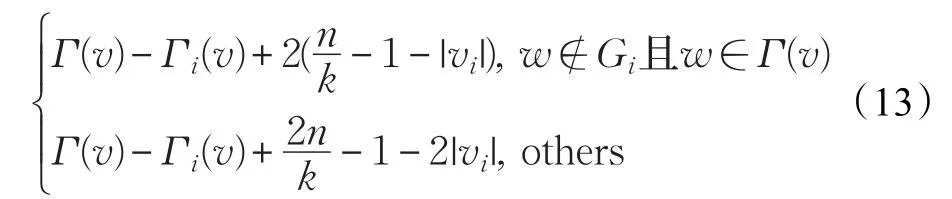
（2）為方便尋找能夠產生最大增益的頂點，IKGGGP算法采用鄰接表的方式記錄每個節點最大增益值產生時所對應的相關信息。其中一維數組的每個元素對應最大增益范圍內的一個值，并且這些值按降序排列。同時，每個元素指向一個雙向鏈表，用于存儲產生相同最大增益值的頂點信息。本文將最大增益頂點按降序排列可以方便選擇產生最大增益的頂點，采用雙向鏈表是為了方便刪除處理過的頂點。

4.2 動態圖分割

實際應用中，RDF數據是在不斷變化的。對應的圖分割算法也應該針對這些變化給出合理的解決方案，以保證數據分割一直滿足邊割和平衡性的要求。本文針對RDF圖動態變化（元組的插入和刪除兩方面，更新操作可以用刪除和插入實現）設計了RDF圖的動態分割及調整策略（Dynamic Partitioning and Adjustment Strategy of RDF，DPAS）。

4.2.1 插入元組insert（s，p，o）

新增元組插入到原RDF圖中分三種情況：（1）新增元組的主語和賓語在原始圖中存在；（2）新增元組的主語或賓語只存在一個；（3）新增元組對應的主語和賓語都不存在。

（1）s和o都存在

當s，o在分割圖中已經存在時，插入元組就是在圖中增加一條邊。如果s,o∈Vi，則增加元組不改變目標函數，因此直接插入該元組即可。如果 s∈Vi，o∈Vj，且i≠j，需要判斷以下情況，選擇增益值最大的一種情況添加。

①不移動頂點，直接在s和o之間添加一條邊，?g增益值為-1。

②將頂點s或o遷移到對方所在分區（頂點遷移的前提是滿足負載均衡條件）時，?g的增益值變化如公式（14）：

（2）s或o中有一個是新頂點

設已經存在的頂點為s，s∈Vi，待加入新節點為o，則頂點o有兩種分區選擇。一種是將o加入到分區i，另一種將o加入到其他某一分區。產生的增益值如公式（15）。同樣，在保持負載均衡的前提下選擇具有最大增益值的分區。

（3）s和o都是新頂點

如果一個元組的主語和賓語都不存在，說明這兩個頂點和圖中任意一個頂點都沒有關聯，分配策略是將這兩點分配到具有最少頂點的分區。

4.2.2 刪除元組delete（s，p，o）

刪除元組就是刪除由頂點s指向o的一條有向邊，如果 |Γ(s)|＞1且 |Γ(o)|＞1，并且 s和 o分別屬于不同的分區，則刪除邊e可以降低整體邊割又不影響分割平衡性，因此直接刪除邊e即可。

當|Γ(s)|=1并且|Γ(o)|=1，或者滿足 s和o的一個頂點鄰域為1時，需要將鄰域為1的頂點連同邊一起刪除。邊割的降低會提高圖的分割質量，但頂點的刪除有可能導致分割的負載失衡。又由于插入元組只是局部調整節點的分配，因此經過一個時間間隔T，圖分割有可能出現局部最優的情況。為避免上述情況的發生，每經過時間T，將對圖進行一次動態調整。

（1）平衡性調整

由于元組的刪除，會導致分割子圖不均衡。如果存在子圖Gi不滿足負載均衡的要求，需要對其進行調整。當|Vi|＜「n(1-e)/k?時，用 Γ(Vi)表示子圖 Gi的鄰域頂點集合。?v∈Γ(Vi)，P(v)=j，當將頂點v從分區j移至分區i時，目標函數的增益值為：

從Γ(Vi)中選擇能夠產生最大增益值的頂點v，將其移到分區Gi中，直到|Vi|滿足公式（3）。

相反，當子圖Gi中的頂點 |Vi|＞「n(1+e)/k?時，用η(Vi)表示子圖Gi中與其他子圖有關聯的頂點集合。?v∈η(Vi)，?u∈Γ(v)，P(u)=j,j≠i，當將 v從分區 i移至分區 j時，目標函數的增益值為：

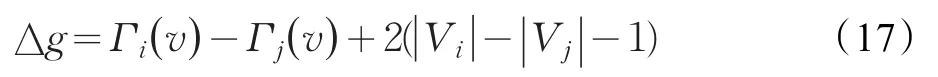
同樣從η(Vi)中選擇能夠產生最大增益值?g的頂點v，將其加入到分區Gj中，直到|Vi|滿足公式（3）。

（2）子圖緊密性

當圖分割滿足負載均衡條件時，分割子圖內部頂點應具有緊密的聯系，而子圖之間頂點聯系應該比較稀疏。本文用子圖的內聚度和耦合度來衡量分割子圖的緊密性。公式（18）和（19）分別給出計算分割子圖內聚度和耦合度的方法。

對于任意分割子圖，如果它的內聚度大于它與其他子圖之間的耦合度，則說明子圖內部頂點聯系比較緊密。當存在子圖的內聚度低于它與其他子圖的耦合度時，說明該子圖內部存在一些頂點，這些頂點與其他子圖聯系更加緊密。

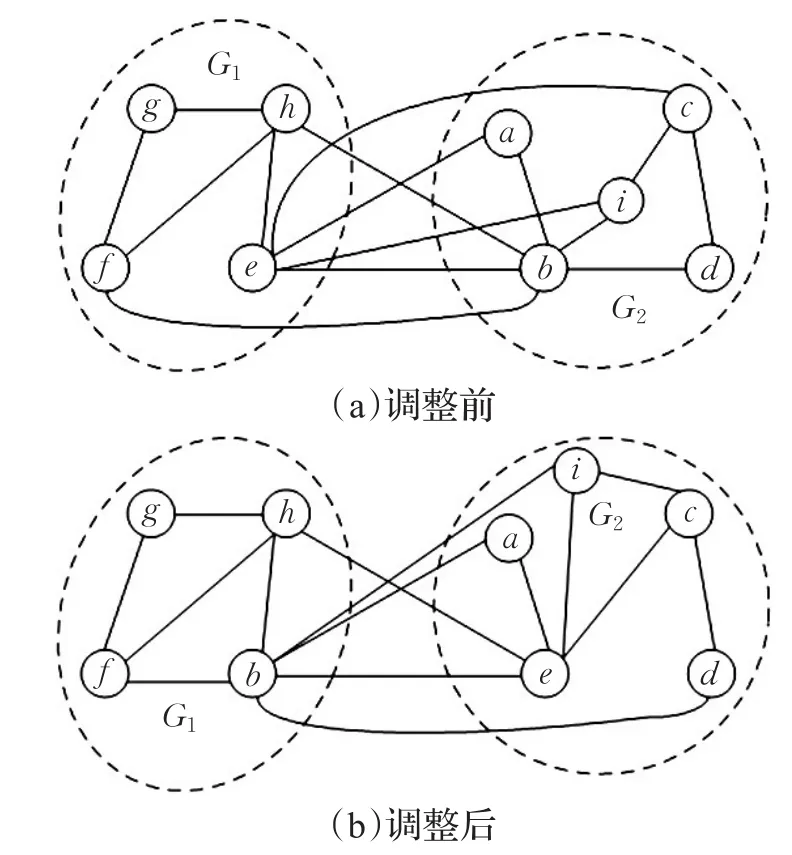
圖3 平衡性調整整

圖3 （b）是交換（a）中兩個分割子圖G1和G2中頂點b和e的結果。對于分割子圖G1，其在交換節點前的內聚度和耦合度分別是4/10和6/10。當交換頂點后，兩個值分別為5/10和5/10。同理，子圖G2也由5/11和6/11變成5/10和5/10。由此可見，G1和G2的內聚度都提升了，而耦合度下降了，最直觀的體現即兩個子圖之間的邊割降低了。

用η(Vi)表示子圖Gi中與其他子圖相關聯的頂點集合。 ?v∈η(Vi)，u∈Γj(v )，j=1,2,…,k且 j≠i，如果 Γ(u)＜Γ(v )，并且u、v在子圖Gi和Gj的鄰域滿足公式（20），就將頂點u和v進行交換。

調整子圖內聚度步驟如下：

步驟1根據公式（18）和（19）計算分割子圖內聚度及子圖間耦合度。

步驟2如果存在子圖cohesion(Gi)＜connection(Gi,Gj)，j=1,2,…,k且 j≠i，執行步驟3；否則，跳轉到步驟5。

步驟3如果存在v∈η(Vi)，u∈Γj()v 并且 Γ(u)＜Γ()

v ，同時滿足公式（20），則交換頂點u和v；否則轉到步驟5。

步驟4更新子圖內聚度及子圖之間耦合度，跳轉到步驟2。

步驟5輸出調整后的分割結果。

5 實驗

本文實驗選取合成數據集（LUBM）和真實數據集（Uniprot）驗證RGPDOO算法在分割靜態和動態RDF圖時的性能。

5.1 數據集及實驗環境

LUBM是一種標準化的評價語義網算法的合成數據集。利用其提供的數據生成器可以生成不同規模大小的RDF數據集。Uniprot是一個可免費訪問的關于蛋白質序列和功能信息的真實數據集。表1列出了這兩個數據集的一些基本信息。

表1 實驗數據表

本文的實驗運行硬件環境為：Inter Xeon 2.00 GHz×24處理器，20 GB內存；軟件環境為：Linux操作系統，C++編程語言。

5.2 實驗結果及分析

5.2.1 靜態分割IKGGGP性能驗證

本文選擇LUBM50和Uniprot子集（一億條元組）對靜態圖分割算法IKGGGP進行了驗證。實驗中選擇METIS，MLP+METIS和BRGP作為對比算法，參數ε=0.3，δ=2m/n。每個分割算法執行三次，取結果的平均值，平衡性取最大子圖與分割子圖的均值比，四種算法均將數據集分割成4、8和16三種不同大小的分區。圖4給出了四種算法在分割時間、邊割量和平衡性三方面的對比結果。如圖4所示，IKGGGP算法分割時間優于METIS，低于MLP+METIS和BRGP。IKGGGP、MLP+METIS和BRGP的執行效率與圖中頂點度數的分布沒有直接關系，因此不受圖中高度頂點的影響。而METIS算法的頂點粗化速度直接受頂點度數的影響[18]。對于本文的兩個數據集，數據集中存在一些高度頂點，這些頂點的度數是普通頂點的幾十甚至幾百倍，因此造成METIS算法分割效率低于其他三種算法。其中MLP+METIS和BRGP算法中依靠標簽傳播算法（LPA）來實現頂點的逐層粗化，每層LPA的時間復雜度為O(tm)，其中t為LPA算法迭代次數，m對應的是每一層圖中的邊數。IKGGGP算法需要先計算頂點與其鄰域之間的相似性找出核心點，然后再進行節點分配，時間復雜度為O(m+n)。但IKGGGP算法之所以在效率上仍高于MLP+METIS和BRGP，原因在于IKGGGP算法在對待分配頂點進行分配時，需要不斷更新待分配頂點的最大增益值。另外，IKGGGP算法的分割效率與待分配頂點的數目有關，圖5列出了初始分割時所產生的三類頂點占頂點總數的比例。從圖5可以看出，內核頂點隨著分區數目的增加在逐漸降低，但總量仍然超過30%，因此在對頂點進行分配時，至少有30%的頂點不參與再分配，這也是IKGGGP算法時間效率高于METIS的一個原因。

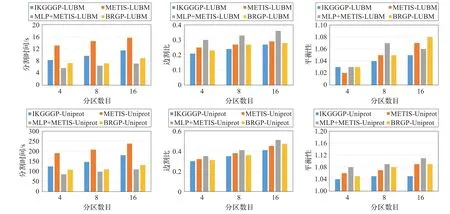
圖4 IKGGGP初始分割算法性能驗證

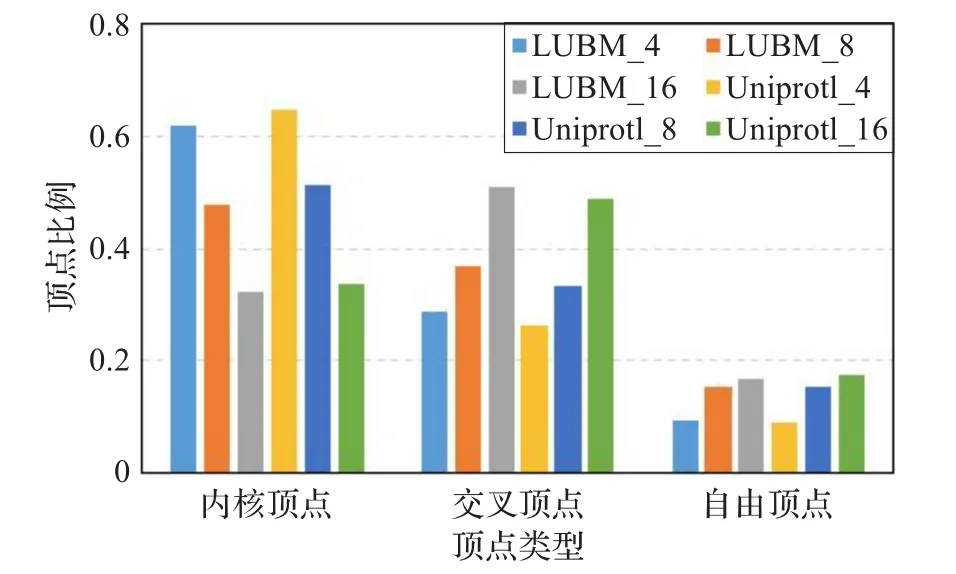
圖5 初始分割三類頂點統計

在邊割和負載均衡的結果中IKGGGP算法要優于其他三種算法，其原因在于IKGGGP算法中引入的增益函數是直接選擇邊割和負載均衡最優的情況進行頂點分配，而標簽傳播則是間接地實現邊割和負載均衡的最優，因此IKGGGP算法的邊割和負載均衡在幾種算法中占有一定優勢。

5.2.2 動態圖分割DPAS性能驗證

本部分驗證RGPDOO算法動態分割及調整策略DPAS。DPAS是在已有分割圖的基礎上，根據RDF圖的動態變化執行的。因此，以IKGGGP圖分割結果為基礎，通過不斷向圖中插入元組，驗證DPAS的性能。本部分選擇Spinner和Fennel兩種動態圖分割算法作為比較算法。實驗中DPAS、Spinner將LUBM50和Uniprot1作為初始靜態數據，其他數據都以動態插入方式產生。Fennel以流方式直接增加數據，最終插入的數據量使LUBM數據集達到LUBM2000，Uniprot數據集達到Uniprot2，DPAS的動態調整時間間隔設為T=5 s。圖6顯示了三種算法在分割時間，邊割和平衡性三方面的實驗結果。其中，Fennel在兩種數據集上的分割效率都是最高的，其原因在于Fennel算法采用流式分割，時間效率是線性的。而Spinner的分割效率要低于Fennel和DPAS，主要是由于Spinner在數據變化后，每次都重啟迭代，重新尋找最優分割，因此效率會隨著節點數目的增加逐漸降低。RGPDOO算法在靜態圖數據分割中采用的IKGGGP算法效率不高，但動態圖分割部分由于DPAS采用線性的節點分配方案，頂點的調整也是基于局部子圖，因此其效率介于Spinner和Fennel之間。

圖6 IRGPA算法性能驗證

在邊割和平衡性的實驗結果中，DPAS的分割效果明顯好于其他兩種算法。雖然Fennel算法也是基于邊割和平衡目標函數進行分割的，但DPAS在算法中增加了動態調整功能，使整體分割不至于陷入局部最優。而Spinner基于標簽的平衡性是以邊為基準的，本文比較以節點為主，因此Spinner平衡性要低于DPAS與Fennel。

圖7 動態調整對圖平衡性影響

上述實驗DPAS在運行期間都是執行元組插入操作，為驗證元組刪除及動態調整有效性，本文每隔時間T，采用隨機的方式從分割圖中刪除若干元組。圖7給出了執行動態調整前后圖分割平衡性變化情況。從圖中可以看出，調整前由于元組的刪除，圖頂點的數目下降，導致最大子圖失衡程度上升。當DPAS增加了動態調整功能后，圖分割的平衡性會比調整前有所降低，使整體圖分割的平衡性始終維持在一個變化范圍內。

5.2.3 RGPDOO在增量圖分割中性能驗證

5.2.1 小節實驗表明IKGGGP算法在初始圖分割時的效率要低于MLP+METIS和BRGP算法。但其邊割和負載均衡性都要優于其他三種算法。然而隨著數據量的不斷增加，將IKGGGP初始分割結果作為后續圖分割的基礎，增加的數據采用DPAS進行動態分割，MLP+METIS、METIS和BRGP面對增量數據采用重新分割的方式進行比較，分割效率有了明顯的變化。圖8分別顯示了LUBM和Uniprot兩個數據集在幾種不同分割算法上將數據集分割成8個分區時的時間性能。其中RGPDOO選擇LUBM50數據集和Uniprot1的一億條數據作為初始靜態分割的數據集。METIS、MLP+METIS和BRGP算法對應不同規模大小數據集的分割時間都是直接將算法作用于相應數據集所得到的分割時間。由圖中曲線可以看出，隨著數據集規模的增加，RGPDOO算法分割時間增加緩慢，而METIS、MLP+METIS和BRGP算法的分割時間明顯高于RGPDOO。并且數據集越大，越顯示出RGPDOO算法的優勢。其原因在于IRGPA的增量圖分割算法部分在計算節點分配時，只考慮很少一部分與待分配相關聯的節點，因此分割速度很快，而其他的三種算法當數據規模變化時，需要通過更多的迭代得到最終結果，增加了算法的運行時間，由此也說明RGPDOO在增量數據分割時的有效性。

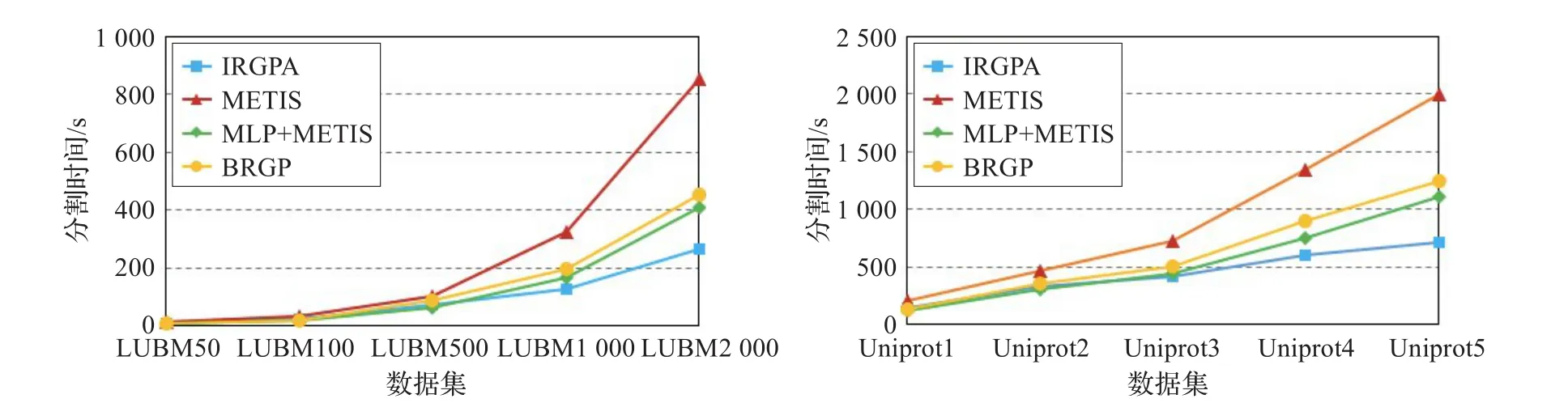
圖8 IRGPA增量分割效率

6 結束語

本文從RDF圖分割的兩個基本目標：邊割和平衡性出發，提出一種基于雙目標優化的RDF圖分割算法（RGPDOO）。RGPDOO將邊割和分割平衡兩項圖分割指標融合到一個目標函數，并依據此目標函數，實現了RDF圖的靜態和動態分割。其中靜態圖分割改進了KGGGP算法，不僅通過節點初始分區降低了候選節點集規模，而且通過選擇雙目標函數增益值實現了候選節點的分配。對于動態分割部分，本文依據目標函數給出了元組插入和刪除時節點的分配策略（DPAS）。同時，為了避免局部最優或分割失衡，DPAS每隔時間T，都會依據分割平衡性和子圖內聚度對子圖進行動態調整，以保證圖分割始終滿足最小化邊割和分割平衡兩項目標。實驗選擇了兩種常用的數據集進行測試，分別從分割效率、邊割和平衡性三方面驗證了靜態和動態圖分割算法的性能。結果表明RGPDOO能夠實現RDF圖的有效分割。但同其他分割算法相比，RGPDOO的分割效率略低于其中一些算法，這也是今后研究的方向。

[1]RDF[EB/OL].http：//www.w3.org/TR/rdf-concepts/.

[2]Yu L.Linked open data.A developer’s guide to the semantic web[M].Berlin Heidelberg：Springer，2011：409-466.

[3]Lee K，Liu L，Tang Y，et al.Efficient and customizable data partitioning framework for distributed big RDF data processing in thecloud[C]//IEEE Sixth International Conference on Cloud Computing，2013：327-334.

[4]Lee K.Efficient data partitioning model for heterogeneous graphs in the cloud[C]//High Performance Computing，Networking，Storage and Analysis，2013：1-12.

[5]Wu B，Zhou Y，Yuan P，et al.Scalable SPARQL querying using path partitioning[C]//International Conference on Data Engineering.IEEE，2015：795-806.

[6]Huang J，Abadi D J，Ren K.Scalable sparql querying of large rdf graphs[J].Proceedings of the VLDB Endowment，2011，4（11）：1123-1134.

[7]Wang L，Xiao Y，Shao B，et al.How to partition a billionnode graph[C]//2014 IEEE 30th International Conference on Data Engineering（ICDE），2014：568-579.

[8]朱牧，孟凡榮，周勇.基于鏈接密度聚類的重疊社區發現算法[J].計算機研究與發展，2013，50（12）：2520-2530.

[9]Tsourakakis C，Gkantsidis C，Radunovic B，et al.FENNEL：streaming graph partitioning for massive scale graphs[C]//ACM International Conference on Web Search and Data Mining，2014：333-342.

[10]張曉媛，張珩，翟健.基于鄰域的大規模圖數據動態分割算法[J].計算機系統應用，2016，25（9）：193-199.

[11]Martella C，Logothetis D，Loukas A，et al.Spinner：scalable graph partitioning in the cloud[J].Computer Science，2015.

[12]Pujol J M，Erramilli V，Siganos G，et al.The little engine（s） that could：scaling online social networks[J].IEEE/ACM Transactions on Networking，2012，20（4）：1162-1175.

[13]Yang S，Yan X，Zong B，et al.Towards effective partition management for large graphs[C]//Proceedings of the 2012 ACM SIGMOD International Conference on Management of Data，2012：517-528.

[14]Xu N，Chen L，Cui B.LogGP：a log-based dynamic graph partitioning method[J].Proceedings of the VLDB Endowment，2014，7（14）：1917-1928.

[15]Predari M，Esnard A.A k-way greedy graph partitioning with initial fixed vertices for parallel applications[C]//Euromicro International Conference on Parallel，Distributed，and Network-Based Processing，2016：280-287.

[16]Zhou Y，Cheng H，Yu J X.Graph clustering based on structural/attribute similarities[J].Proceedings of the VLDB Endowment，2009，2（1）：718-729.

[17]Khosravi-Farsani H，Nematbakhsh M，Lausen G.SRank：Shortest paths as distance between nodes of a graph with application to RDF clustering[J].Journal of Information Science，2013，39（2）：198-210.

[18]Yao L，Wang Z，Li Z，et al.A novel coarsening scheme for multilevel graph partitioning[C]//International Conference on Biomedical Engineering and Informatics，2011：2091-2094.

CHEN Zhikui1,LENG Yonglin1，2

1.School of Software Technology,Dalian University of Technology,Dalian,Liaoning 116620,China 2.College of Information Science and Technology,Bohai University,Jinzhou,Liaoning 121000,China

RDF graph partitioning algorithm based on double objective optimization.Computer Engineering and Applications,2017,53（21）：24-31.

Distributed storage is a more effective method for the mass data storage.And,the data partitioning is the premise of distributed storage.In facing of the growing semantic web data,RDF Graph Partitioning algorithm is proposed by Double Objective Optimization（RGPDOO）.RGPDOO fuses edge cut and load balancing together to get an objective function.According to this objective function,RGPDOO achieves static and dynamic partitioning of RDF graph.For the static partitioning,an initial partitionis executed to divide the node into three kinds：kernel nodes,boundary nodes and freedom nodes.And then,the boundary and freedom nodes are distributed to apartition with the max gain of objective function.For the dynamic partitioning,the insertion and deletion solution of triples are given by the objective function.And,RGPDOO will execute a dynamic adjustment at a certain time interval according to the balance and tightness of partitioning subgraph to satisfy the partitioning object.Finally,the algorithm is tested on synthetic and real datasets in comparison with several general graph partitioning algorithms.The experimental results show that RGPDOO is more suitable for RDF graph partitioning.

RDF graph;static partitioning;dynamic partitioning;edge cut;load balancing

A

TP311

10.3778/j.issn.1002-8331.1706-0426

國家自然科學基金（No.U1301253，No.61672123）；廣東省科技計劃（No.2015B010110006）；國家重點研發計劃（No.2016YFD0800300）；遼寧省博士科研啟動基金項目（No.201601348，No.201601349）。

陳志奎（1968—），男，博士，教授，研究領域為物聯網理論與應用、云計算與大數據處理，E-mail：zkchen@dlut.edu.cn；冷泳林（1978—），女，博士研究生，副教授，研究領域為數據存儲與索引，不完整數據填充。

2017-06-30

2017-09-25

1002-8331（2017）21-0024-08