基于時空優化深度神經網絡的AQI等級預測

董 婷，趙儉輝，胡 勇

1.武漢大學 計算機學院，軟件工程國家重點實驗室，武漢 430072 2.武漢大學 資源與環境科學學院，武漢 430079

基于時空優化深度神經網絡的AQI等級預測

董 婷1，趙儉輝1，胡 勇2

1.武漢大學 計算機學院，軟件工程國家重點實驗室，武漢 430072 2.武漢大學 資源與環境科學學院，武漢 430079

針對現有空氣質量預測方法精度偏低、對噪聲敏感等問題，提出一種基于堆棧降噪自編碼（Stacked Denoising Auto-Encoders，SDAE）模型的空氣質量等級預測方法。首先以武漢市歷史空氣質量和氣象監測數據為研究對象，建立SDAE模型逐層學習原始數據的特征表達，并將最后一層特征與分類器連接完成預測模型的調優。同時改進多參數網格搜索法，選取了最優的超參數組合。然后在測試集上進行預測，并用預測值與實際值之間的平均絕對誤差和均方誤差等指標作為預測性能評價標準。通過與其他網絡模型的實驗對比，證明了SDAE模型對于空氣質量等級具有較優的預測性能。最后從時間、空間、時空三個角度對該模型輸入進行優化，實驗結果表明基于空間優化的SDAE模型預測性能提升最為明顯，能夠得到比傳統方法更加精確的預測結果。

AQI等級；預測；堆棧降噪自編碼；優化

1 引言

近幾年霧霾天氣頻發，如果長時間在高濃度污染物環境下活動，容易對人體健康造成直接危害[1-2]，對空氣質量等級準確地預測不僅可以幫助公眾提前了解未來空氣質量情況并合理安排戶外活動，還可以在預測到重污染等級天氣后通知環保局等有關部門采取措施，預防或減緩危害事件的發生。空氣質量指數（Air Quality Index，AQI）是一種用來評測空氣狀況的指標，參與空氣質量評價的主要污染物有細顆粒物（PM2.5）、可吸入顆粒物（PM10）、二氧化硫（SO2）、二氧化氮（NO2）、臭氧（O3）、一氧化碳（CO）六項。空氣質量按照AQI大小分為六級：一級（0～50）優、二級（51～100）良、三級（101～150）輕度污染、四級（151～200）中度污染、五級（201～300）重度污染，六級（＞300）嚴重污染。指數越大、級別越高說明空氣污染情況越嚴重，對人體健康的危害也越大。AQI與氣象條件有極大關系[3]。不同氣象狀況下污染物擴散條件不同，排入相同數量的污染物，空氣中的污染物濃度也會有不同。比如靜穩天氣條件下風力微弱，容易出現逆溫層，不利于顆粒物的擴散，重污染天氣易發。而對于風力大、對流強的地區和時段，大氣擴散稀釋能力強，此時空氣質量相對污染物排放量不會像靜穩天氣下那么敏感。所以，對空氣質量等級進行預測需要結合氣象條件。

對于空氣污染物的預測問題，國內外大多采用傳統的數值預報和回歸統計模型[4-5]。數值預報模型的準確率很大程度依賴于污染源的排放數據，該類數據獲取的復雜性和不確定性使得數值預報在實際應用中受到限制。回歸統計模型需要通過大量分析建立影響因子與污染物濃度之間復雜的線性或非線性關系，由于難以用確定的數學模型描述這種關系，建模難度較大。近年來，基于神經網絡技術的空氣污染物預測研究發展迅速，研究表明，人工神經網絡比傳統的回歸模型性能更好。Azid[6]等將主成分分析和神經網絡相結合建立了馬來西亞空氣污染指數API的預測模型。Mishra[7]等分別采用多元線性回歸分析和人工神經網絡對印度新德里的PM2.5濃度進行預測，實驗證明神經網絡的預測結果更好。

神經網絡具有很強的非線性擬合能力，能夠映射復雜的非線性關系，但隨著神經網絡層數的增加，梯度下降算法可能會收斂到局部極小值，帶來的誤差會導致結果比淺層網絡更差，同時神經網絡還有過擬合、泛化能力差、收斂速度慢等缺點[8]。近幾年快速發展起來的深度學習理論，已經在計算機視覺、語音識別、自然語言處理等領域得到廣泛應用[9-11]。深度學習通過組合低層特征形成更加抽象的高層表示，以發現數據的分布式特征表示[12-13]。利用深度學習，可以對大量的空氣質量和氣象歷史數據進行智能分析和歸納總結，通過解讀復雜非結構性數據，挖掘出空氣質量指數與各污染物因子以及溫度、濕度、風速等氣象條件之間的內在關系，并建立起AQI與各影響因子之間的復雜計算模型，從而訓練一個有效的深度學習模型來對空氣質量進行預測。尹文君[14]等基于限制玻爾茲曼機建立深度信念網絡對空氣質量分因子進行預測，驗證了DBN對空氣污染預報的有效性。截止目前，深度學習在空氣質量預測領域的應用仍然較少。

由于空氣質量或氣象監測數據存在噪聲，本文提出用堆棧降噪自編碼器建立深度學習網絡模型SDAE。SDAE最大特點是具有降噪功能，即以一定概率分布隨機擦除原始輸入數據，使得數據產生破損，在一定程度上減輕了訓練數據與測試數據的差異性，可以提取并編碼出更具有魯棒性的特征，實現對空氣質量等級更加準確的預測。

2 堆棧降噪自編碼預測模型

2.1 SDAE模型結構

自編碼器（AE）通過捕捉可以代表輸入數據的最重要特征，使輸出盡量復現輸入信號，AE包含編碼和解碼兩個過程：其中“編碼”是指提取輸入數據的特征，而“解碼”是為了驗證提取的特征是否可以很好表示輸入數據。AE訓練過程的最終目標是最小化重構誤差，實質上就是縮小輸入數據X與其特征表達之間的差別。

AE有一個很大的局限性，因為輸入等于輸出，所以該模型很可能會學習到沒有編碼功能的恒等映射。降噪自編碼器（DAE）是在AE的基礎上給輸入數據加入噪聲，也就是以一定的概率分布隨機擦除輸入層的某些節點。此時編碼器會自動學習去除噪聲，從而獲得沒有被噪聲污染的輸入信號。訓練好后的降噪編碼器可以從含噪聲的輸入中提取到更具魯棒性的特征，提升了自編碼神經網絡模型對輸入數據的泛化能力。DAE跟AE的區別如圖1所示。

圖1 傳統自編碼器與降噪自編碼器的區別

堆棧降噪自編碼模型（SDAE）是將多個去除輸出層的DAE堆疊到一起構成的深度學習網絡模型，把上一個DAE隱含層的輸出作為下一個DAE的輸入，通過逐層提取特征，從而得到更抽象的數據特征。當每一層都完成訓練后，將最后一個隱含層的輸出作為頂層有監督層的輸入，用有監督的反向傳播算法對整個網絡進行微調，使得學習到的特征更優。當整個網絡特征學習過程結束后，最后一個隱含層輸出即為最終代表原始輸入的特征。

2.2 基于SDAE的空氣質量預測模型

2.2.1 模型應用

關于預測模型輸入，由于某一天的空氣質量，除了與前一天的空氣狀況和氣象因子有關，與預測當天的氣象條件也有較強的相關性，加之現有氣象預報準確率較高，可為空氣質量預測提供有效參考。本文建立的SDAE模型輸入與文獻[14]類似，每條數據分為三部分：第一部分為某天的AQI值、空氣質量等級、各污染物因子大小等當天空氣質量數據；第二部分是當天氣象數據；第三部分是預報的第二天氣象數據。以2015年1月1日為例，輸入數據格式如表1所示。輸出數據為預測的第二天空氣質量等級。預測結果與記錄的實測數據進行對比，可用于分析預測算法的性能。

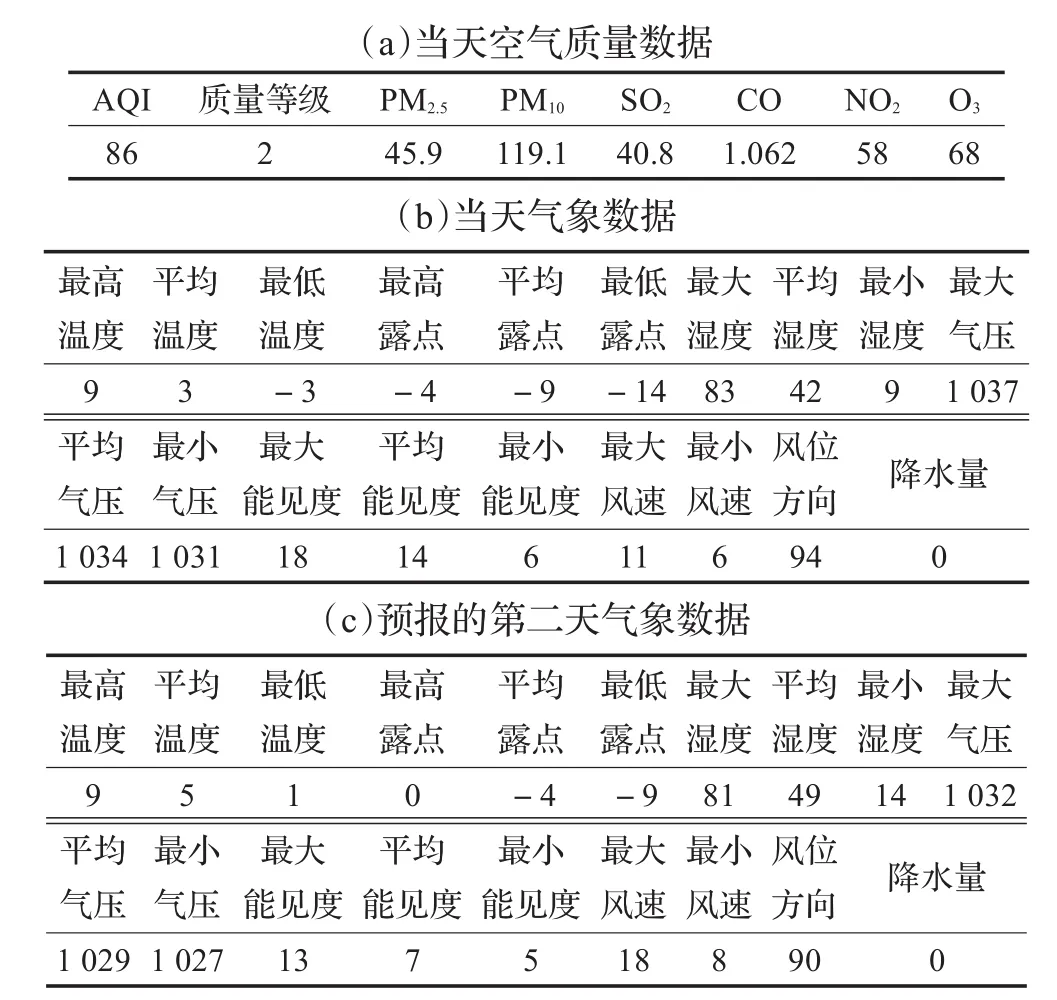
表1 輸入數據格式

綜上所述，本文所建立的AQI等級預測模型結構如圖2所示，該模型的前半部分由多個DAE堆疊而成。輸入層Input和Hidden Layer1構成了第一個DAE，Hidden Layer1和Hidden Layer2構成了第二個DAE，依次類推。h(i)表示第i個DAE學習到的特征，最后一個隱含層的輸出作為下一步操作的輸入。由于全國各地出臺的空氣污染預警方案大多以AQI等級作為預警級別的劃分依據，因此本文在堆棧降噪自編碼網絡的最頂層連接一個分類預測器，把學習到的最終特征作為監督算法的輸入，以此實現AQI等級預測功能。最常用的多分類器是softmax和多邏輯回歸分類器。本文預測模型中，六個等級之間無重合，所以選用softmax分類器。用于訓練分類器的樣本集是堆棧降噪自編碼提取到的特征集，對于代價凸函數，通過迭代算法得到全局最優解之后，就可以得到訓練好的softmax分類器。

2.2.2 模型訓練

該預測模型的訓練過程分為兩步：

（1）無監督逐層預訓練。每層作為一個DAE模型進行訓練，目的是最小化上層輸出在該層的重構誤差。每次訓練一層，只有當第i層訓練完成后，才可以訓練第i+1層。

（2）有監督微調。當每一層都完成訓練后，將最后一個隱含層的輸出作為頂層有監督層的輸入，有監督的訓練softmax分類器，并使用反向傳播算法對整個網絡進行微調，使得學習到的特征更優。

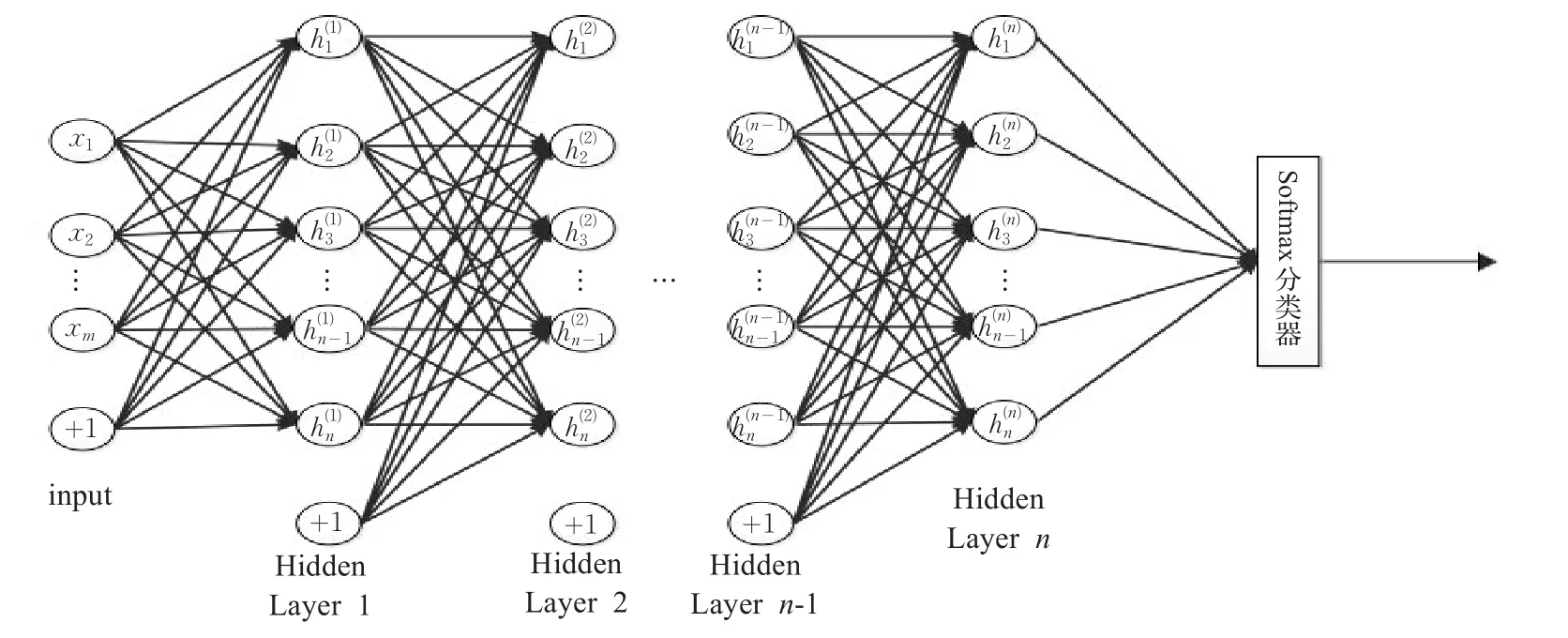
圖2 SDAE預測模型

3 預測模型設置

3.1 預測性能指標

本實驗測試數據中，有接近一半的空氣質量為2級，通過對全國各地空氣質量等級歷史數據的分布統計，這與現實情況是相符的。對于這樣的測試集，即使不訓練學習模型而直接把每一天空氣質量都預測為2級，也能得到47%的準確率，因此僅用準確率來判斷預測模型的性能好壞顯然是不合適的。本文在訓練模型時，采用平均絕對誤差（Mean Absolute Error，MAE）和均方誤差（Mean Squared Error，MSE）作為預測精度的評估標準，其中平均絕對誤差的計算公式如下：

均方誤差的計算公式如下：

以上兩個公式中，n為數據長度，也就是測試集的天數，xi為第i天空氣污染指數等級真實值，xi'為第i天空氣污染指數等級的預測值。

3.2 超參數選取

深度神經網絡中，選取合適的超參數是比較困難但又極其重要的一步，這直接影響到神經網絡模型的性能，但是目前理論上還沒有一種科學的和普遍的超參數確定方法。以往研究[15-16]對于深度網絡超參數的選取基本都帶有經驗性、偶然性，對于網絡結構的確定通常會作為一個獨立的環節，而未考慮其他超參數的影響。但是深度神經網絡中網絡層數、隱含層節點數、學習率、訓練迭代次數等參數之間具有相關性，且大多時候沒有明顯規律。為了避免參數選擇的盲目性和隨意性，本文改進多參數網格搜索法進行參數選取。該方法先對每個參數選取典型區間、典型步長的值，將超參數組合所在的空間維度劃分為合適的網格，然后遍歷網格中的每一個點并比較擇優，初步得到若干個較優的網格點。該方法的第二步是在找到的較優超參數網格點附近，進行基于更細網格的二次遍歷，得到若干更優的參數組合，再通過比較選取最優的一組。這種參數選取方法在很大程度上避免了局部最優問題，可以保證選取的參數組合比較理想，從而避免較大誤差。

圖3以二維網格為例演示了二次搜索超參數組合的過程，多維網絡與此相似。本文設計自動測試程序，按網格搜索方式測試每一組超參數組合并記錄MAE、MSE。在一次搜索完成后，在表現良好的超參數（如左圖中紅點）附近進行更精細的二次搜索，通過二次搜索，可以找到更優的超參數組合（如右圖中綠點）。由于參數組合眾多，本方法相當于犧牲了遍歷時間，從而換得了較高的準確率。本文網格參數的選取參考了文獻[17-18]中列出的部分典型值，詳見表2。通過二次網格搜索算法，最終可以確定當隱含層層數為3、節點數為50且每層輸入加噪率為10%時，SDAE預測模型的預測性能最優。

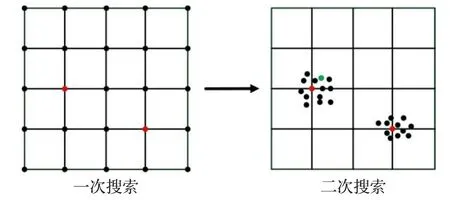
圖3 二維網格二次搜索

表2 超參數典型值

根據表1輸入數據格式，SDAE預測模型輸入層神經元個數為46；最優隱含層層數和隱層神經元個數經二次網格搜索法確定為3和50；預測輸出為空氣質量指數的6個等級，因此輸出層神經元個數為6。綜上，本文建立的堆棧降噪自編碼預測模型的網絡結構為[46 50 50 50 6]。

堆棧降噪自編碼網絡對每一層輸入數據加入噪聲，編碼器通過學習去除噪聲可獲得輸入數據更具魯棒性的特征表達。實驗證明，預報性能與每一層加入的噪聲大小有關，存在最優加噪率，使得平均絕對誤差和均方誤差達到最小。用二次網格搜索法確定的網絡模型超參數中，最優噪聲為10%，為了驗證該參數選取的準確性，在同等條件下選取不同大小的噪聲依次進行實驗。結果如圖4所示，預測誤差類似于一條上開口的拋物線，且在5%和10%處誤差值最小，與加噪率為0（不加噪聲）時相比，性能有明顯提升。

圖4 加入不同噪聲后的預測性能

4 基于SDAE的時空優化策略

考慮到輸入數據在時間與空間方面具有關聯性，本文從時間、空間、時空結合的角度提出了四種相應的優化策略，為深度神經網絡模型的學習提供更多相關信息。

時間優化（Temporal Optimization，TO）：當前時刻的空氣質量會受到過去一段時間的影響，在污染物擴散條件差的情況下，時間影響范圍相應變大。從模式識別角度來講，增大時間粒度有可能發現和提取出更多有用的特征。為了確定合適大小的時間粒度，在基于前一天數據建立的SDAE預測模型基礎上，又分別建立時間屬性為2天和3天的模型，并為每種模型選取二次網格搜索結果中預測誤差最小的前30組進行統計。實驗結果如圖5所示，時間粒度為2天的模型，不論最優MAE、MSE還是平均MAE、MSE，預測誤差均比時間粒度為1天和3天的模型小，因此以2天為時間劃分基數對模型輸入數據進行優化調整，建立TO-SDAE時間優化模型。

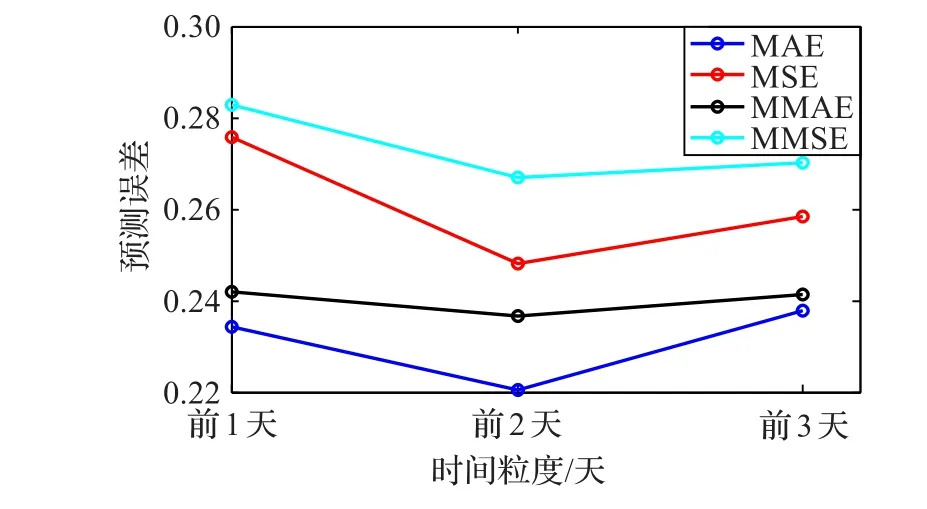
圖5 不同時間粒度下的時間優化模型性能

空間優化（Spatial Optimization，SO）：受氣象條件影響，空氣污染因子具有擴散性，目標城市的空氣質量會受到周邊區域影響。因此基于單個城市的空氣質量預測存在一定局限性，需要對SDAE模型進行空間上的優化。以武漢為中心點，對周邊城市按直線距離進行排序，由近至遠依次為南昌、長沙、合肥、鄭州等（由于數據來源限制，本文只考慮省會城市），并針對武漢及周邊最近的1、2、3、4個城市的數據分別建立不同空間粒度下的優化模型，為每種模型選取二次網格搜索結果中預測誤差最小的前30組進行統計。實驗結果如圖6所示，可以看出，空間粒度為3天的模型預測誤差各指標均為最小，因此以周邊3城市為空間粒度對模型輸入數據進行優化調整，建立SO-SDAE空間優化模型，此時模型輸入除了武漢自身數據外，還包括長沙、南昌、合肥三個城市的相關數據。

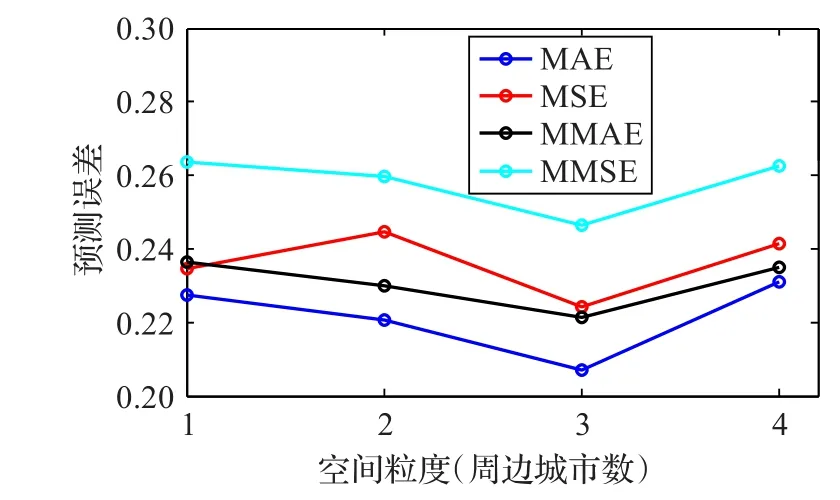
圖6 不同空間粒度下的空間優化模型性能

全局時空優化（Global Spatio-Temporal Optimization，GSTO）：前文針對時間優化模型，確定了基于前2天數據的最佳時間優化粒度；針對空間優化模型，確定了基于周邊3城市數據的最佳空間優化粒度。基于這兩種優化策略的啟發，從時空結合的角度對模型進行優化。即預測武漢市第i+1天的空氣質量等級時，輸入數據包括武漢、長沙、南昌、合肥四個城市前兩天的空氣質量和氣象因子歷史數據，以及預測當天的氣象預報數值。基于這種優化策略，建立GSTO-SDAE時空優化模型。

局部時空優化（LocalSpatio-Temporal Optimization，LSTO）：針對全局時空優化過程中可能引入的關聯度較低數據，提出一種局部時空優化策略，即選取時間和空間上的關鍵信息，排除關聯度低的輸入信息對模型造成的干擾，建立LSTO-SDAE局部時空優化模型。具體而言，輸入數據包括武漢市第i-1天的空氣質量和氣象因子數據（不包括周邊3城市第i-1天的信息），武漢、長沙、南昌、合肥四個城市第i天的空氣質量和氣象因子數據，以及預測當天的氣象預報數據。

圖7展示了GSTO-SDAE和LSTO-SDAE兩種時空優化模型的輸入區別。LSTO-SDAE認為周邊城市時間較遠的數據對于預測武漢市空氣質量的影響不大，因此不予考慮。

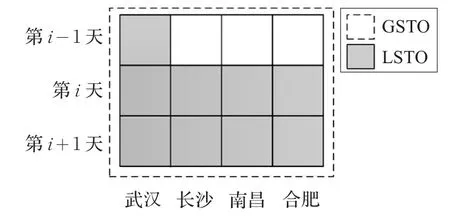
圖7 全局與局部時空優化模型輸入數據區別

5 實驗與結果分析

5.1 實驗數據預處理

本文對武漢市2013年12月至2016年9月日均空氣質量相關數據和氣象數據即污染物擴散條件信息進行收集，選擇2013年12月至2015年11月的730條數據作為深度神經網絡的訓練數據，剩余的290條數據作為測試數據。

影響空氣質量的因子眾多，且每個因子具有各自的物理性質和量綱，如果直接拿這些數據進行分析，會影響結果的準確性。為便于網絡訓練，防止計算過程出現“過擬合”等問題，需先對原始數據進行歸一化處理，讓不同影響因子處于同一數量級，以便進行更精確的數據分析。本文采用Min-Max標準化方法，也就是對原始數據的各屬性進行一種線性變換，經過標準化之后的數據處于[0，1]之間，標準化函數如下：

其中x是歸一化之前的數據，x'是歸一化之后的數據，min是x所屬影響因子中所有數據的最小值，max是x所屬影響因子中所有數據的最大值。

對訓練集做歸一化后，相應的也要對測試數據進行同樣的標準化，從而保證測試數據與訓練集同比例縮放。但是大多數空氣質量和氣象數據的值沒有確切邊界，對于個別小于訓練集最小值或大于最大值的測試數據，為了其歸一化能落在[0，1]區間內，在上式基礎上增加如下限制：

5.2 不同網絡模型預測性能對比

為了驗證基于堆棧降噪自編碼網絡模型的預測效果，將優化前的SDAE模型與傳統神經網絡（Neural Network，NN）、深度信念網絡（Deep Belief Network，DBN）以及堆棧自編碼網絡（Stacked Auto-Encoders，SAE）相比。在對比實驗中，對所有網絡模型結構超參數的確定，統一采用上文提出的二次網格搜索法，得到最優參數組合。為了使對比實驗更合理，消除僅對比最優預測結果可能導致的偶然性，本文對各網絡模型分別選取了二次網格搜索結果中預測誤差最小的前30組，對比其總體性能分布。平均絕對誤差和均方誤差箱形圖如圖8、9所示，SDAE的最優預測性能、平均預測性能和模型穩定性均明顯優于其他幾種網絡。

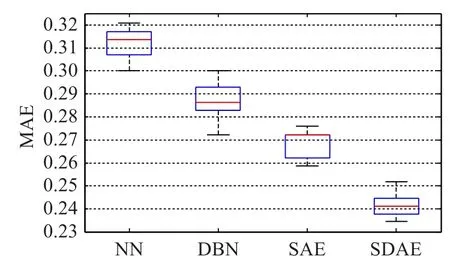
圖8 四種網絡模型平均絕對誤差對比

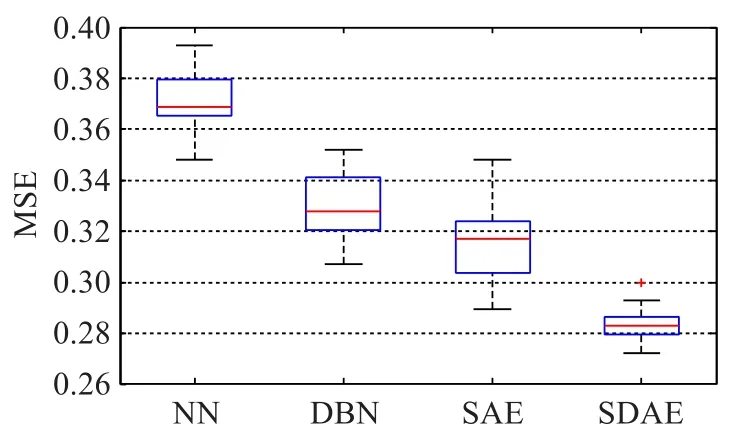
圖9 四種網絡模型均方誤差對比

5.3 不同優化策略下SDAE模型性能對比

針對本文提出的四種空氣質量預測時空優化策略，分別建立對應的預測模型。與之前實驗類似，為了實驗結果的可靠性，每種優化模型選取二維網格搜索結果中預測誤差最小的前30組，并與優化之前的SDAE相比，得到如下箱形圖。從左至右分別是優化前的SDAE模型、基于時間優化策略的TO-SDAE模型、基于空間優化策略的SO-SDAE模型、基于全局時空優化策略的GSTOSDAE模型和基于局部時空優化策略的LSTO-SDAE模型，五種網絡輸入層節點分別為46、73、184、292、211。基于圖10和圖11的實驗對比，發現以下結果。

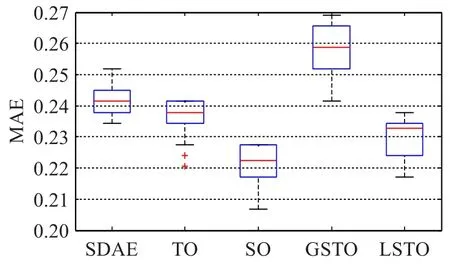
圖10 四種優化策略平均絕對誤差對比

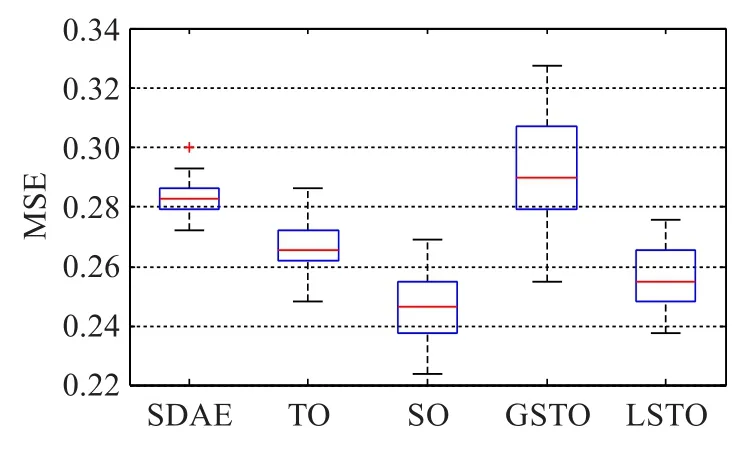
圖11 四種優化策略均方誤差對比

本文提出的四種優化策略中，時間優化、空間優化和局部時空優化這三種模型均比優化前的SDAE模型預測性能更優。其中基于空間優化的模型性能提升最大，局部時空優化次之，時間優化性能提升較小。分析原因，由于本文實驗數據為日均數據，以天為單位進行空氣質量預測時，AQI在時間上的關聯性較差，不如空間關聯性緊密，因此基于空間優化策略的性能提升更加明顯。

基于全局時空優化的模型性能較差，原因是在輸入數據中引入了關聯度較低的數據，對模型提取輸入特征造成了干擾，致使預測性能下降。基于局部時空優化的模型性能好于全局時空優化，但仍低于空間優化，原因仍在于以天為單位數據的時間關聯性較差，從而影響了局部時空優化的性能。

5.4 優化模型與其他預測方法的對比

采用基于空間優化策略的SO-SDAE模型作為預測模型，在測試數據集上進行驗證，并對所有預測值和實際值的差值進行統計，結果如圖12所示。在290天的測試數據中，有233天的空氣質量等級能被準確預測，54天會被錯誤預測為相鄰等級，只有3天的預測誤差為2個等級，沒有3級及以上誤差，總體預測性能較優。

文獻[19]分別用當前常用的空氣預測方法：綜合指標法（Comprehensive Index Method，CIM）和逐步回歸法（Stepwise Regression Method，SRM）建立了AQI等級預報統計模型。其中CIM采用了擬合率作為預測性能評價指標，即將AQI等級1～2級認定為空氣質量好，3～6級為空氣質量差，正確預測到第二天空氣狀況（好與差）的天數占總天數的比例。SRM采用了各誤差級數占比作為評價指標，即預測級數與真實級數之差的絕對值分別為0（準確率）、1、2、3及以上的天數占總天數的比例。本文采用完全一樣的評價指標，與文獻[19]的方法進行對比，結果如表3所示。可見本文提出的基于空間優化的SO-SDAE預測模型的擬合率高于CIM，準確率高于SRM模型，其余誤差級數所占比例整體低于SRM模型。與優化前的SDAE模型相比，SO-SDAE的擬合率和準確率均有較明顯的提升，同時誤差級數占比減少，尤其是誤差為2級的天數從6天縮減為3天，減少一半。

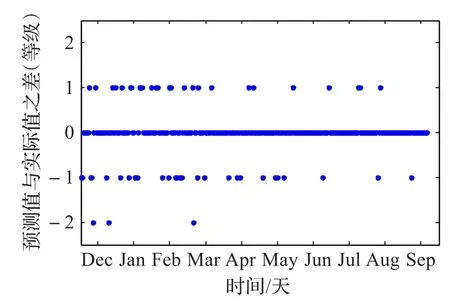
圖12 預測值與實際值的誤差統計

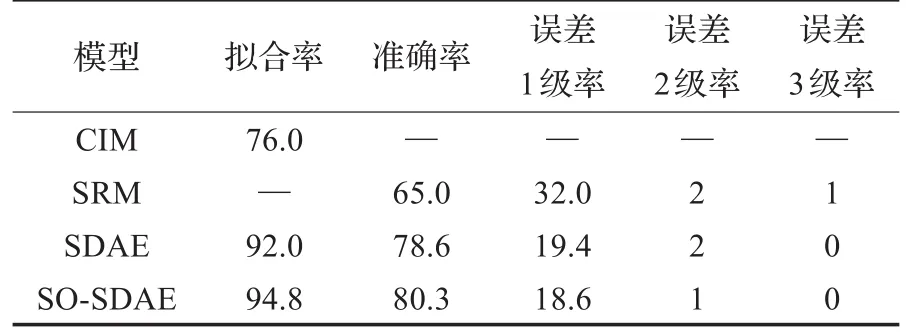
表3 幾種預測方法的性能對比%

6 結論

本文提出一種基于時空優化的堆棧降噪自編碼空氣質量預測模型。利用無監督學習算法的優勢，自動對有噪聲的輸入數據逐層提取特征，通過訓練學習建立起空氣質量等級與污染物因子濃度、氣象數據之間的關系模型。采用武漢地區空氣質量數據進行實驗分析，通過實驗對比，得出以下結論：

（1）以MAE、MSE作為預測性能評價標準，證明了基于SDAE的空氣質量等級預測模型比BP、DBN、SAE三種網絡模型的預測性能更優、結果更穩定。

（2）基于時間、空間、局部時空三種優化策略的SDAE預測模型與優化之前相比，性能均有提升，其中基于空間優化的模型性能最優。從全局時空優化實驗結果可以看出，如果輸入引入關聯度較低的數據，會對模型的特征提取造成干擾，導致預測效果較優化前變差。

（3）以擬合率、準確率和不同誤差級數占比作為預測性能評價標準，依次與綜合指標法和逐步回歸法預測模型進行對比，證明了本文提出的基于空間優化的SDAE模型預測性能更好。

隨著今后更多監測數據的積累，可以得到空氣質量各等級更充足的數據，從而使深度神經網絡模型學習到每個等級更具代表性的特征表達，以此對各級污染天氣做出更加精準的預測。此外，如果基于更大量樣本的學習，例如以小時為單位的污染物和氣象數據，以及省會城市之外的更多城市的監測數據，將會得到精度更高的預測結果，尤其會提升時空模型的性能。

[1]Kelly F J，Fussell J C.Air pollution and public health：Emerging hazards and improved understanding of risk[J].Environmental Geochemistry and Health，2015，37（4）：631-649.

[2]Mclaren J，Williams I D.The impact of communicating information about air pollution events on public health[J].Science of the Total Environment，2015，538：478-491.

[3]Gilliam R C，Hogrefe C，Godowitch J M，et al.Impact of inherent meteorology uncertainty on air quality model predictions[J].Journal of Geophysical Research：Atmospheres，2016，120（23）：259-280.

[4]Pérez V A，Arasa R，Codina B，et al.Enhancing air quality forecasts over Catalonia（Spain）using model output statics[J].Journal of Geoscienceamp;Environment Protection，2015，3（8）：9-22.

[5]Xu Bin，Luo Liangqing，Lin Boqiang.A dynamic analysis of air pollution emissions in China：evidence from nonparametric additive regression models[J].Ecological Indicators，2016，63：346-358.

[6]Azid A，Juahir H，Toriman M E，et al.Prediction of the level of air pollution using principal component analysis and artificial neural network techniques：A case study in Malaysia[J].Water，Air，amp;Soil Pollution，2014，225（8）：2063.

[7]Mishra D，Goyal P，Upadhyay A.Artificial intelligence based approach to forecast PM2.5 during haze episodes：A case study of Delhi，India[J].Atmospheric Environment，2015，102：239-248.

[8]盧輝斌，李丹丹，孫海艷.PSO優化BP神經網絡的混沌時間序列預測[J].計算機工程與應用，2015，51（2）：224-229.

[9]奚雪峰，周國棟.面向自然語言處理的深度學習研究[J].自動化學報，2016，42（10）：1445-1465.

[10]吳財貴，唐權華.基于深度學習的圖片敏感文字檢測[J].計算機工程與應用，2015，51（14）：203-206.

[11]Karpathy A，Toderici G，Shetty S，et al.Large-scale video classification with convolutional neural networks[C]//IEEE Conference on Computer Vision and Pattern Recognition（CVPR）.Piscataway，NJ：IEEE，2014：1725-1732.

[12]Lecun Y，Bengio Y，Hinton G.Deep learning[J].Nature，2015，521（7553）：436-444.

[13]馬世龍，烏尼日其其格，李小平.大數據與深度學習綜述[J].智能系統學報，2016，11（6）：728-742.

[14]尹文君，張大偉，閆京海，等.基于深度學習的大數據空氣污染預報[J].中國環境管理，2015，7（6）：46-52.

[15]戴曉愛，郭守恒，任淯，等.基于堆棧式稀疏自編碼器的高光譜影像分類[J].電子科技大學學報，2016，45（3）：382-386.

[16]王山海，景新幸，楊海燕.基于深度學習神經網絡的孤立詞語音識別的研究[J].計算機應用研究，2015，32（8）：2290-2291.

[17]Vincent P，Larochelle H，Lajoie I，et al.Stacked denosing autoencoders：Learning useful representations in a deep network with a local denoising criterion[J].Journal of Machine Learning Research，2010，11（6）：3371-3408.

[18]Bengio Y.Practical recommendations for gradient based training of deep architectures[M]//Neural Networks：Tricks of the Trade.Berlin：Springer-Verlag，2012：437-478.

[19]黃菊梅，陳姣絨，彭潔，等.岳陽市區空氣質量變化特征及氣象條件預報[J].環境科學與技術，2016，39（6）：168-173.

DONG Ting1,ZHAO Jianhui1,HU Yong2

1.State Key Laboratory of Software Engineering,School of Computer Science,Wuhan University,Wuhan 430072,China 2.School of Resources and Environmental Sciences,Wuhan University,Wuhan 430079,China

AQI levels prediction based on deep neural network with spatial and temporal optimizations.Computer Engineering and Applications,2017,53（21）：17-23.

The existing air quality prediction models have lower precision,and sensitive to noisy data.Thus a new method is proposed for AQI levels prediction based on Stacked Denoising Auto-Encoders（SDAE）model.Firstly,the historical air quality and meteorological monitoring data of Wuhan city are taken as research object.SDAE model is established to study the characteristic expression of the original data layer by layer,and the last layer is connected with a classifier to tune the prediction model.The optimal set of hyper-parameters is found through improved grid search algorithm for multiparameters.Then,the prediction is obtained from the test set.The indicators such as mean absolute error and mean square error between the predicted value and related actual value are used as the evaluation standards for forecasting performance.Compared with other network models,it can be proved that SDAE model has better predictive performance.Finally,the input data is optimized considering their spatial and temporal relations.Experimental results show that the spatial optimization based SDAE has the most improvement for predictive performance,and it can obtain more accurate predictions compared with the traditional methods.

AQI levels;prediction;Stacked Denoising Auto-Encoder（SDAE）;optimization

A

TP391

10.3778/j.issn.1002-8331.1705-0420

中國空間技術研究院創新基金（No.CAST2014）；湖北省科技支撐計劃（No.2014BAA149）；中央高校基本科研業務費專項（No.2042016gf0023）。

董婷（1992—），女，碩士研究生，研究領域為深度學習及應用、圖像處理，E-mail：dongtingwhu@163.com；趙儉輝（1975—），男，博士，副教授，研究領域為人工智能、圖形圖像；胡勇（1973—），男，博士，副教授，研究領域為空間模型與模擬、氣候變化適應與減緩。

2017-05-31

2017-09-19

1002-8331（2017）21-0017-07