流場環境對柔性立管濕模態的影響

陳東陽，Laith K.Abbas，王國平，芮筱亭

(南京理工大學 發射動力學研究所，江蘇 南京 210094)

流場環境對柔性立管濕模態的影響

陳東陽，Laith K.Abbas，王國平，芮筱亭

(南京理工大學 發射動力學研究所，江蘇 南京 210094)

為了研究靜水壓力和瞬態流場載荷對三維柔性立管濕模態的影響，本文基于聲-固耦合模型對考慮水介質、頂張力情況下的立管進行濕模態計算，并與理論計算結果以及實驗數據對比，驗證了該模型的準確性；采用不考慮流-固耦合的計算流體力學(computational fluid dynamics, CFD)方法和考慮流固雙向耦合的計算流體力學/計算結構力學(computational fluid dynamics/computational structure dynamics,CFD/CSD)方法分別計算了立管的瞬態流場載荷，并與實驗數據對比；將水深產生的靜水壓力和瞬態流場載荷分別加載到三維柔性立管表面進行靜力學分析，計算其濕模態。計算結果表明：立管濕模態頻率比干模態頻率小很多,且隨著頂張力增大而增大； 靜水壓力和瞬態流場載荷都使得濕模態頻率略微增加；靜水壓力和瞬態流場載荷對濕模態低階振型影響較大，對高階振型幾乎沒有影響。

濕模態； 聲-固耦合模型； 渦激振動； 頂張力； 柔性立管； 瞬態流場載荷； 湍流模型； 干模態

海洋立管是海洋平臺進行海底油氣輸送的重要設施和關鍵部分，它是連接海底管線或海底井口與海洋平臺之間的輸送管道。立管內部一般有高溫、高壓的油氣流過，外部承受波浪、海流及風等環境載荷的作用[1]。在內外流的作用下立管有可能產生流固耦合振動，當立管固有頻率與外界激勵力頻率接近時，就會發生振動“鎖定”現象，使得振幅顯著加大，從而導致立管的疲勞破壞，造成立管失效。因此，立管的振動特性研究對結構的性能分析、動態設計具有重要意義。

模態分析是進行復雜動力學問題分析的前提和基礎[2-3]。由于海洋立管位于海洋環境中，因此計算需要考慮立管周圍流體對海洋立管動態特性的影響，也就是濕模態特性[4-5]。海洋環境對海洋立管振動特性的影響主要來自于流體水動力載荷作用于立管表面引起的預應力效應，以及流體隨同立管振動引起的附加質量效應[6-7]。

自20世紀70年代以來，隨著計算機技術和數值模擬技術的迅猛發展，基于計算流體力學(computational fluid dynamics, CFD)理論的數值模擬已成為研究復雜流場的重要手段。目前，CFD技術已具備模擬三維粘性流場繞流的能力，為海洋立管三維圓柱繞流提供精確的海洋環境流體響應載荷，成為研究海洋立管渦激振動的重要工具[8-10]。

本文對立管的流場環境進行了計算。基于尺度自適應模擬(scale-adaptive simulation, SAS)，分別計算了將立管視為剛體和柔性體兩種情況下的流體載荷響應。分析了水動力載荷和水深對立管振動特性的影響。

1 濕模態計算模型

1.1幾何模型及參數

本文以Bijan Sanaati的實驗模型為研究對象[13]。立管的兩端邊界為鉸-鉸約束，同時立管頂端頂張力大小為T，如圖1所示。PVC管結構參數、周圍流體環境參數、內部流體介質參數見文獻[13]。

圖1 三維立管模型Fig.1 3D model of the riser

1.2聲-固耦合模型及邊界條件

當海洋立管處于真空中時，計算出的模態為干模態，而當海洋立管位于海洋環境中時，需要考慮立管內外水介質對立管振動特性的影響，因此必須采用濕模態法對其動力特性進行分析。聲-固耦合模型中，水為無粘不可壓縮流體，并且通過Kinsler假定，將流體的動量方程(Navier-Stokes)和連續性方程簡化為聲波方程：

(1)

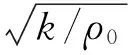
將聲波方程離散化[14],得到

(2)

結構本身的動力學方程為

Msü+KsU=Fs+RP

(3)

將式(2)、(3)聯立：

(4)

式中：s代表結構，f代表流體；M、K分別表示質量矩陣、剛度矩陣；P為聲學壓力矩陣，F為力的矩陣，U為位移矩陣，R為流固耦合界面的耦合矩陣，代表流固界面上每個節點處的有效面積，它將界面上的流體壓力轉換成結構的載荷。濕模態計算由Ansys軟件完成。

幾何模型由3部分組成，如圖2所示，分別是立管外部流體介質、立管內部流體介質和立管本身。立管周圍流體介質采用圓柱形，以方便畫網格時候，采用切塊和掃略方法能夠生成較好的網格。圖3為立管與立管內外流體介質網格局部放大圖。其中PVC管采用18 734個SOLID 186單元，PVC管內部流體介質采用的是34 510個FLUID 220單元，PVC管外部流體采用的是85 061個FLUID 220單元。 FLUID 220是高階20節點，每節點具有3個位移、一個壓力共4個自由度的聲學實體單元。只有流固交界面上的位移自由度才有效，所以對于該單元的節點，除了落在交界面上的隨結構移動之外，其他都是固定在空間一點的。流固耦合交界面上的流體單元被定義為耦合單元，流固耦合交界面上的所有節點被定義為流固耦合(fluid structure interaction，FSI)載荷的作用點。在材料庫中定義了水的密度和水中聲速，以及立管內部介質的密度和該介質中聲速。

為計算考慮立管頂張力情況下的濕模態。首先，對立管進行頂張力作用下的靜力學分析，并以靜力學計算結果更新數值模型的剛度和質量矩陣，然后進行濕模態分析。計算流體載荷和水深對立管濕模態的影響，也采用同樣的方法。

2 流-固雙向耦合模型

2.1流體域模型

Menter借鑒DES模型中長度尺度的思路[15]，基于剪切應力傳輸(shear stress transfer， SST)湍流模型提出了一種尺度自適應模擬方法(scale-adaptive simulation，SAS)，它是一種新的(reynolds average navier-stokes/large eddy simulation, RANS/LES)混合模型，SAS模型長度尺度不依賴于計算單元的大小，可以依靠流動狀態動態自適應調整湍流黏性，并克服了RANS/LES 交界面問題，且SAS模型遠場處耗散小，從而可以自適應的分辨湍流結構。

圖2 立管與立管內外流體介質幾何模型Fig.2 Geometric model of the riser and its internal and external fluid

圖3 網格局部圖Fig.3 Partial part of mesh diagram

SST-SAS湍流模型實際上只在標準SST湍流模型的基礎上修改其ω方程，在Lvk方程的源項中增加一項QSAS

[16]。

(5)

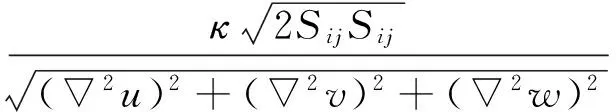
(6)

(7)

式中：Lvk和L分別為von Karman尺度和模化湍流力尺度，具體動力學模型方程、模型常數ζ2、κ、C、σφ、Cμ見文獻[14-15]。

建立PVC立管的外流場，其中PVC管的直徑為D。入口處來流到立管的距離為10D，兩邊到立管的距離也為10D，出口處到立管的距離為30D。進口處采用速度進口邊界條件，出口處采用開放性邊界條件，其他面都采用對稱邊界條件。流體域模型如圖4所示。

流體與壁面間相互作用，很多因變量具有較大的梯度，而且粘度對傳輸過程有很大的影響。采用SST-SAS湍流模型要求近壁處有y+<1。計算網格如圖5所示，在沿著管長方向分布了100個節點。網格數量為2 776 653。

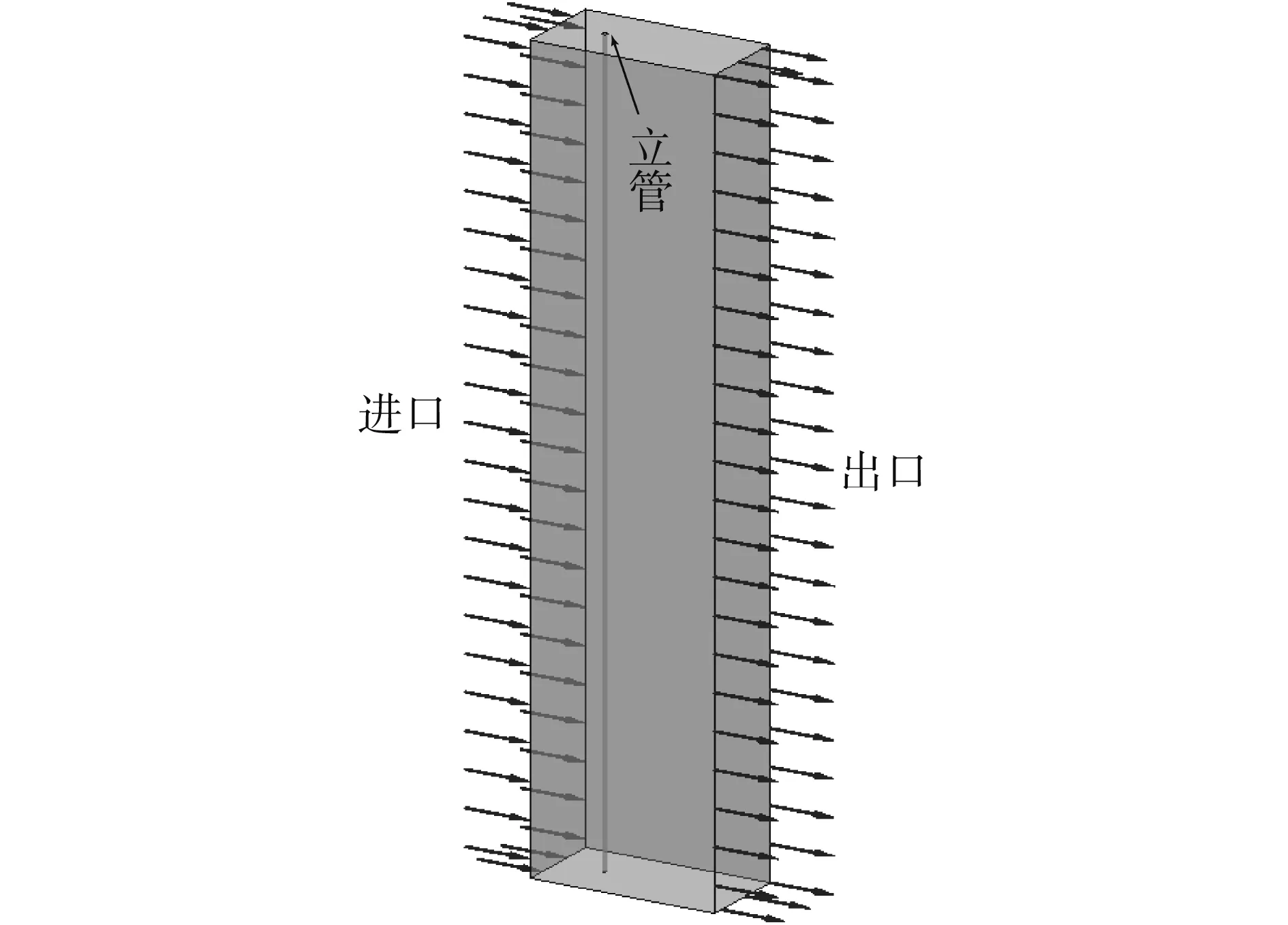
圖4 流體域模型Fig.4 Fluid domain model

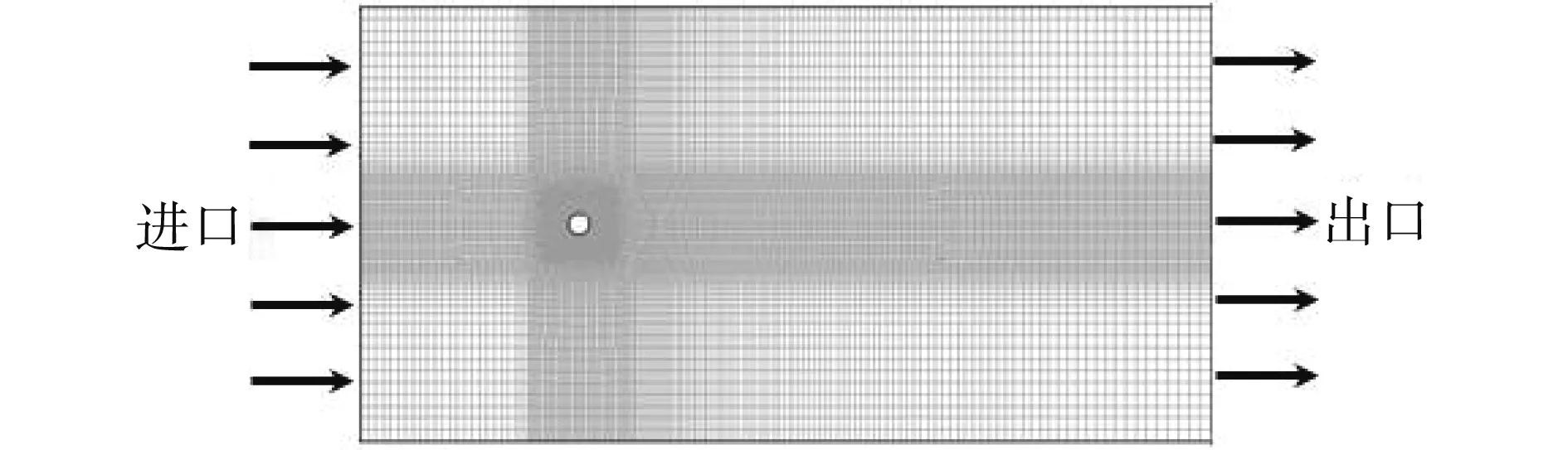
圖5 流體域計算網格Fig.5 Grid of fluid domain

2.2固體域模型

立管的動力學方程為

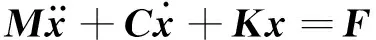
(8)

式(8)中F為作用在立管表面的流體力，由基于SST-SAS的計算流體力學方法計算得到。F隨著時間變化，根據具體的物理作用，F(x,y,z,t)=Ff+FFSI，Ff為來流引起的水動力；FFSI為立管振動加速度和速度引起的輻射力，以及立管振動位移引起的回復力；FFSI可以寫為

(9)

(10)

2.3雙向流固耦合

采用任意拉格朗日歐拉(arbitrary Lagrange-Euler，ALE)法來解決耦合作用問題中由于坐標不統一所帶來的運動界面協調問題。ALE 的基本思想是在流體域采用歐拉單元，在固體域內使用拉格朗日單元，并在統一的 ALE 坐標系下進行求解。ALE 法的優點是可以實現歐拉網格的移動，這樣可以使流體網格根據固體的變形而發生改變。網格運動通過彈簧比擬法實現，為了避免流場中心域和環繞域之間的變形過于迅速造成計算失敗,采取小體積網格單元部分網格剛度系數大，主要靠大體積網格吸收變形的做法。雙向流固耦合流程圖如圖6所示。

圖6 雙向耦合流程圖Fig.6 The flow chart of two-way coupling

3 計算結果及分析

3.1濕模態頻率分析

簡支梁頻率的理論計算公式為

(11)

式中：m為單位長度的流體介質附加質量，工程上一般將圓柱形立管的附加質量簡化為立管外徑對應的圓柱排開流體介質的質量;T為頂張力，M為單位長度的PVC管質量，L為立管長度，E為立管的彈性模量，I為立管的截面慣性矩。該公式只能計算橫向或者縱向的振動頻率，圓柱形立管屬于對稱結構，所以橫向振動頻率與縱向振動頻率一致。

基于聲-固耦合模型，首先計算了鉸-鉸約束、立管頂端不同頂張力情況下的干、濕模態。從圖7(a)可以看出，第一階濕模態頻率比理論公式計算值略小，但更接近于文獻[13]中的實驗數據。但隨著頂張力的加大，和實驗數據相比，誤差增大。由于立管是完全對稱的模型，立管的振動頻率都是每兩階相等的。圖7(b)為三維立管的1、3、5、7階干、濕模態頻率分布。從圖中可以看出，濕模態頻率幾乎都是干模態頻率的一半，隨著立管頂張力的加大，干、濕模態頻率都顯著提高。

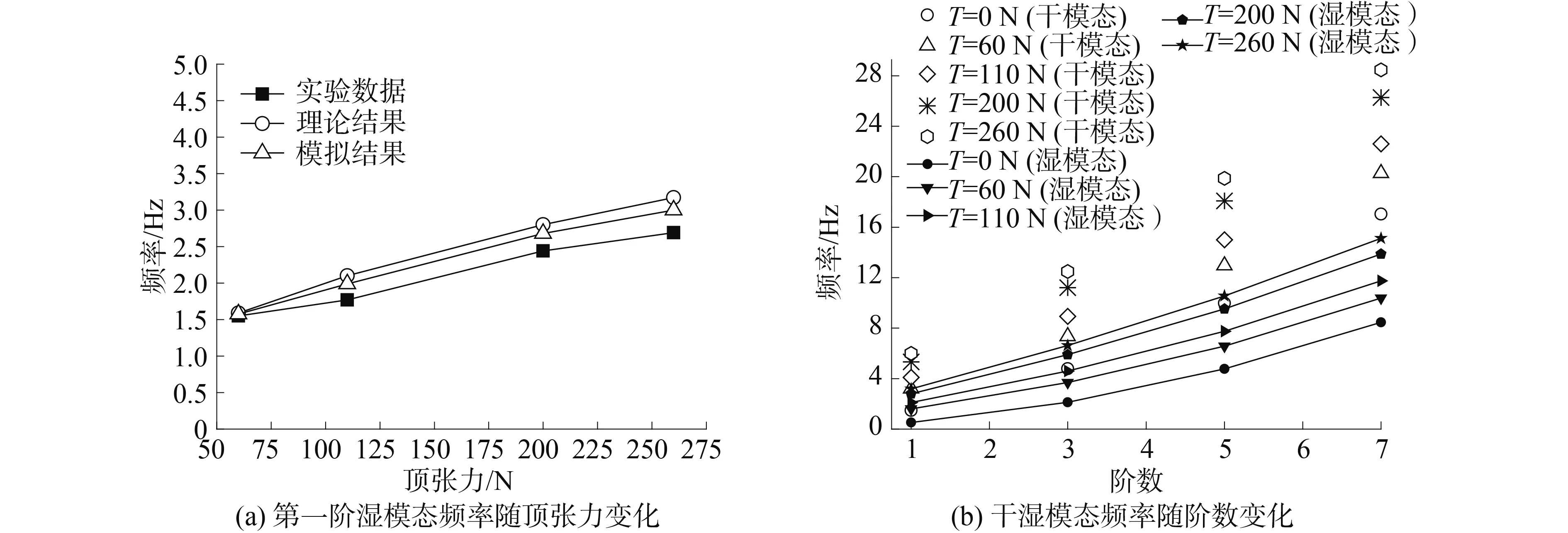
圖7 鉸-鉸約束情況下模擬結果Fig.7 The simulation results in the condition of hinge-hinge constraint

3.2流場環境對立管濕模態的影響分析

3.2.1 基于CFD求解瞬態流場載荷

CFD求解流場參數的原理是，先對流場進行求解，得到流場每一個網格上的速度、密度、壓力等參數，然后通過計算公式求出水動力系數。來流繞過圓柱體，會使得圓柱體產生阻力，同時，流體繞過圓柱體，由于漩渦脫落，使得圓柱橫向產生速度差，從而產生壓力差，導致圓柱橫向產生升力。阻力系數和升力系數的計算公式為

(12)

(13)

式中：CL、CD分別為升力系數、阻力系數，FL,FD分別為升力、阻力，L是立管的長度，D為PVC管的外徑，U為來流速度。

描述圓柱繞流現象的一個重要參數是斯特魯哈數St，St數代表流體的非定常性質。St與漩渦脫落的頻率fs的關系式為

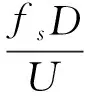
(14)

式中：fs為漩渦脫落的頻率，通過對升力系數時間響應作快速傅里葉(FFT)變換得到。

所有系數的計算公式采用CFX的二次開發CEL語言編寫成CCL文件導入CFX軟件。

首先計算了雷諾數Re為3 900情況下的三維PVC管圓柱繞流流場。計算得到升力系數、阻力系數時程曲線如圖8(a)所示，將升力系數時程曲線作FFT變換得到Re為3 900時的漩渦脫落頻率，如圖8(b)所示。

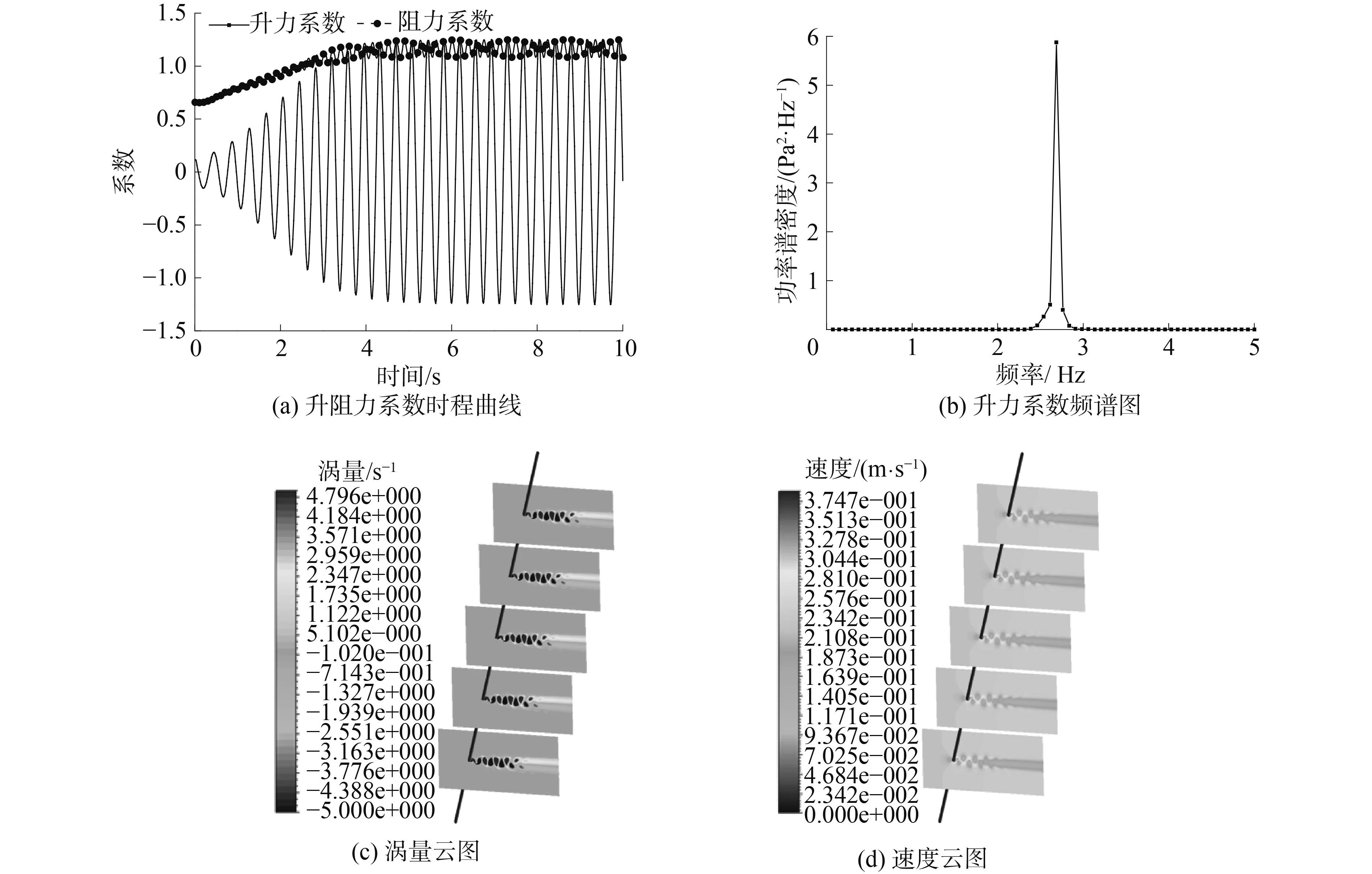
圖8 雷諾數Re=3 900時的計算結果Fig.8 Simulation result of Re=3 900 situation

圖8(c)、(d)分別為Re=3 900時候的渦量云圖及速度云圖。從圖中可以看到漩渦的脫落。利用式(14)計算得到斯特魯哈數St。文獻[17]中,得到的平均阻力系數為0.99，St為0.209；文獻[18]中得到的平均阻力系數為1.26，St為0.22；與本文計算結果阻力系數1.13，St為0.22較為接近，說明計算結果較好，驗證了本文CFD流場模擬的精確性。

3.2.2 基于CFD/CSD雙向耦合求解瞬態流場載荷

橫向振幅的均方根與立管直徑的比值RMSAZ/D(root mean square of amplitude inZdirection devideD)隨著約化速度的變化結果如圖9所示，計算了8組結果，從圖中可以看出，數值模擬的結果與文獻[13]實驗數據對比，誤差值較小。說明基于尺度自適應模擬的雙向流固耦合仿真精度較高。Ur=4.39～12.67之間為本文PVC立管的頻率鎖定區間，該區間內負值相對周圍區間有顯著的增大。本文數值模擬的計算結果都位于鎖定區間。

圖10為T=60 N,U=0.15 m/s時的部分仿真結果，圖10(a)為立管橫向和縱向的振動幅值的無量綱量的均方根(root mean square, RMS)沿著立管長度方向(立管上的位置與立管長度的比值，y/L)的分布，從圖中可以看出，橫向振幅大于來流向振幅，立管最大幅值發生在立管中部，幅值無量綱量為0.42，與Ur=5.43處實驗數據很接近。圖10(b)為立管中間點處的運動軌跡，從圖中可以看出，運動軌跡比較雜亂，橫向和來流向的振動位移響應都比較大，因此單方面只考慮橫向振動的模型不能準確反映立管實際振動情況。圖10(c)為立管橫向振動幅值無量綱量的歷時云圖，從圖中可以看出，該流速情況下，立管主要是以第一階模態振動。

圖9 立管Z方向幅值均方根隨著約化速度變化圖Fig.9 Variation of root mean square of ampitude in Z direction with reduced velocity

圖10 T=60 N, U=0.15 m/s情況下的仿真結果Fig.10 Simulation results of T=60 N, U=0.15 m/s situation

圖11為頂張力T=260 N，來流速度為0.2 m/s時候的三維立管升力系數和阻力系數的時間歷程圖。從圖中可以看出，將立管視為柔性體，基于CFD/CSD雙向耦合方法求得的系數的振幅要比將立管視為剛體情況下的大。立管為柔性體，雙向耦合情況下計算出來的瞬態流場更接近實際情況。

3.2.3 靜水壓力對立管濕模態的影響

以公式P=ρgh計算沿著立管長度方向的靜水壓力分布，施加在立管外表面，然后對立管進行靜水壓力作用下的靜力學分析，并以靜力學計算結果更新數值模型的剛度和質量矩陣，然后進行濕模態計算。計算了不同頂張力情況下，靜水壓力對濕模態的影響。計算結果表明，考慮靜水壓力后，濕模態頻率都會略微變大，變化幅度很小。表3為頂張力等于0 N和260 N情況下，考慮和不考慮靜水壓力的濕模態頻率計算結果，從表中可以看出，考慮靜水壓力后，濕模態頻率略微增大。

圖11 升阻力系數時程曲線Fig.11 Variation of drag and lift coefficient with time

分別計算三維PVC柔性立管考慮和不考慮靜水壓力情況下的振型。計算結果表明，立管的振型主要表現在X和Z兩個方向上。振型的數值比較大的為主振型，數值小的為次振型。考慮靜水壓力對該柔性立管低階振型有影響，這種影響主要體現在次振型上，對主振型幾乎沒有影響。對高階振型的主振型和次振型都沒有影響。圖12中，original one標識不考慮水深影響的立管濕模態振型，hydro pressure表示考慮水深影響情況下的立管濕模態振型。圖中可以看出，第一、二階的次振型在考慮靜水壓力情況下彎曲幅度要比不考慮靜水壓力的情況下大。而考慮和不考慮靜水壓力對第三、四階振型沒有影響。

表3水深對濕模態頻率的影響

Table3Theinfluenceofwaterdepthonwetmodalfrequency

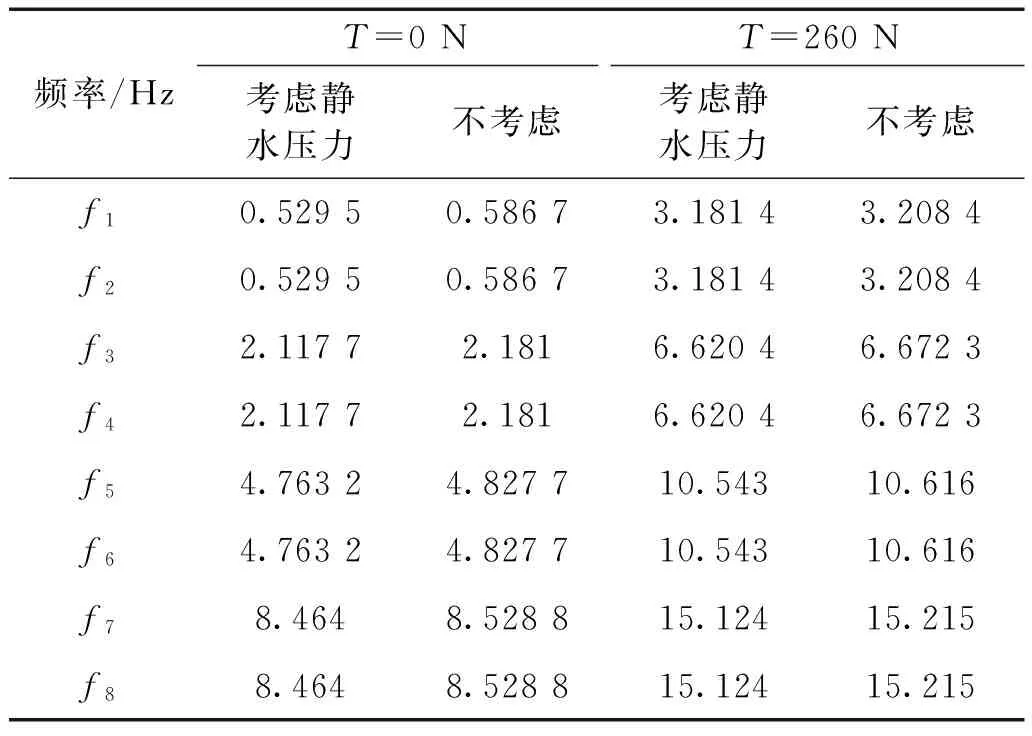
頻率/HzT=0NT=260N考慮靜水壓力不考慮考慮靜水壓力不考慮f10.52950.58673.18143.2084f20.52950.58673.18143.2084f32.11772.1816.62046.6723f42.11772.1816.62046.6723f54.76324.827710.54310.616f64.76324.827710.54310.616f78.4648.528815.12415.215f88.4648.528815.12415.215

3.2.4 瞬態流場載荷對立管濕模態的影響

將前文計算出的瞬態流場載荷插值到三維柔性PVC立管的外表面的有限單元節點上，先進行靜力學分析，再進行濕模態計算。圖13(a)、(b)分別是來流速度為0.2 m/s，頂張力為0 N和260 N時的第一階頻率隨時間變化圖。從圖中可以看出，在瞬態流場作用下，濕模態頻率呈周期性變化，這是由于漩渦脫落引起流體載荷呈周期變化引起的。考慮瞬態流場載荷后，濕模態頻率相對不考慮流場載荷的情況下略微變大，變大幅度極小。隨著頂張力的增加，頻率變化更小。如圖13(b)所示，兩種方法計算出來的瞬態流場載荷(第一種：立管視為剛體計算出的瞬態流場載荷；第二種：立管視為柔性體，雙向耦合計算出的瞬態流場載荷)對濕模態頻率幾乎沒有影響。如圖13(a)所示，采用雙向耦合法計算出的瞬態流場載荷對立管的濕模態頻率影響相比立管視為剛體計算出來的瞬態流場載荷對立管濕模態頻率影響大。將立管視為柔性體，該情況下計算出的瞬態流場載荷對立管濕模態頻率影響的計算結果更符合實際。

圖12 T=0 N情況下的振型Fig.12 Mode shape of T=0 Nsituation

圖13 第一階頻率隨時間變化趨勢Fig.13 Variation of the first mode frequency with time

圖14為T=260 N、U=0.2 m/s、t=5.6 s時的濕模態振型的前四階計算結果。從圖14(a)中可以看出，考慮瞬態流場載荷主要對第一、二階的次振型有影響，對主振型都沒有影響。采用雙向耦合方法計算出的第一、二階次振型彎曲幅度相比不考慮耦合方法計算出的第一、二階次振型彎曲幅度大。從圖14(b)中可以看出，瞬態流場載荷對第三、四階的主振型和次振型都幾乎沒有影響。此結果與水深對立管濕模態振型的影響結果類似。

圖14 T=260 N, U=0.2 m/s時的振型Fig.14 Mode shape of T=260 N, U=0.2 m/s situation

4 結論

1)立管各階模態頻率相比干模態頻率有較大降低，降幅在30%～50%左右。隨著立管頂端的頂張力的增大，立管出現明顯的應力剛化現象，使得立管濕模態頻率有大幅度的增加。

2)考慮靜水壓力使得立管濕模態頻率略微增加。同時，考慮靜水壓力對該柔性立管低階振型有影響，對高階振型沒有影響。

3)分別計算出立管視為剛體和柔性體兩種情況下的瞬態流場載荷，將瞬態流場載荷插值到立管有限單元節點上，進行濕模態分析。濕模態頻率相比不考慮瞬態流場載荷影響的要略微變大，且隨時間呈周期性變化。兩種情況下計算出的瞬態流場載荷對立管的濕模態頻率影響極小，但對濕模態的低階振型影響較大。

[1] 劉德輔, 王樹青, 郭海燕. 海洋立管綜合環境條件設計標準研究[J]. 海洋工程, 2001, 19(2)： 13-17.

LIU Defu, WANG Shuqing, GUO Haiyan. Study on combined design criteria for marine risers conveying flowing fluid[J]. The ocean engineering, 2011, 19(2): 13-17.

[2] 顧海明, 周勇軍. 機械振動理論與應用[M]. 南京: 東南大學出版社, 2007.

GU Haiming, ZHOU Yongjun.Theory and application of mechanical vibration[M]. Nanjing: Southeast University Press, 2007.

[3] 聞邦椿,劉樹英，陳照波，等.機械振動理論及應用[M].北京：高等教育出版社， 2009.

WEN Bangchun, LIU Shuying, CHEN Zhaobo, et al.Theory and application of mechanical vibration[M]. Beijing: Higher Education Press, 2009.

[4] CHEN Y F, CHEN W J, HE Y L, et al. Dry and wet modal analysis and evaluation of influencing factors for flexible airship envelop[J]. Journal of Shanghai Jiaotong University, 2014, 48(2): 1002-1023.

[5] 姜峰, 鄭運虎, 梁瑞,等. 海洋立管濕模態振動分析[J]. 西南石油大學學報, 2015, 37(5): 159-166.

JIANG Feng, ZHENG Yunhu, LIANG Rui, et al. An analysis of the wet modal vibration of marine riser[J]. Journal of Southwest Petroleum University, 2015, 37(5): 159-166.

[6] 張光法. 潛深對半潛器附加質量影響分析[J].艦船電子工程， 2012(11)： 9-10.

ZHANG Guangfa. Analysis ofinfluence of submerged depth on adds mass of semmi-submerged device[J]. Ship electronic engineering, 2012(11)： 9-10.

[7] CHEN D Y, ABBAS L K, RUI X T, et al. Dynamic modeling of sail mounted hydroplanes system-Part I: modal characteristics from a transfer matrix method[J]. Ocean engineering, 2017， 130: 629-644.

[8] HUANG K. Riser VIV and its numerical simulation[J]. Engineering sciences, 2013(4): 55-60.

[9] ZHU H, YAO J, MA Y, et al. Simultaneous CFD evaluation of VIV suppression using smaller control cylinders[J]. Journal of fluids & structures, 2015，57: 66-80.

[10] ZHU H, YAO J. Numerical evaluation of passive control of VIV by small control rods[J]. Applied ocean research, 2015，51: 93-116.

[11] 繆旭弘，錢德進，姚熊亮，等.基于ABAQUS聲固耦合法的水下結構聲輻射研究[J].船舶力學， 2009(2)： 319-324.

MIAO Xuhong, QIAN Dejin, YAO Xiongliang, et al. Sound radiation of underwater structure based on coupledacoustic-structural analysis with ABAQUS[J]. Journal of ship mechanics, 2009(2)： 319-324.

[12] 田紅莉，劉志峰，張乃龍,等.箱體結構的聲固耦合有限元分析[J].機械設計與制造， 2007(7)： 24-26.

TIAN Hongli, LIU Zhifeng, ZHANG Nailong. Solid box on the acoustic coupling finite element analysis[J]. Machinery design & manufacture, 2007(7)： 24-26.

[13] SANAATI B, KATO N. Vortex-induced vibration (VIV) dynamics of a tensioned flexible cylinder subjected to uniform cross-flow[J]. Journal of marine science and technology, 2013, 18(2): 247-261.

[14] CUI X Y, HU X, WANG G, et al. An accurate and efficient scheme for acoustic-structure interaction problems based on unstructured mesh[J]. Computer methods in applied mechanics & engineering, 2017, 317: 1122-1145.

[15] LUCIUS A, BRENNER G. Unsteady CFD simulations of a pump in part load conditions using scale-adaptive simulation[J]. International journal of heat & fluid flow, 2010, 31(6): 1113-1118.

[16] 王翔宇, 李棟. SST-SAS在小分離流動數值模擬中的表現測試[J]. 西北工業大學學報, 2014(3): 337-340.

WANG Xiangyu, LI Dong. Behavior of SST-SAS for mild airfoil trailing-edge separation[J]. Journal of Northwestern Polytechnical University, 2014(3): 337-340.

[17] FRANKE J, FRANK W. Large eddy simulation of the flow past a circular cylinder at Re=3900[J]. Journal of wind engineering and industrial aerodynamics, 2002, 90: 1191-1206.

[18] 詹昊，李萬平，方秦漢，等. 不同雷諾數下圓柱繞流仿真計算[J]. 武漢理工大學學報， 2008, 30(12)： 129-132.

ZHAN Hao, LI Wanping, FANG Qinhan, et al. Numerical simulation of the flow around a cricular cylinder at varies reynolds number[J]. Journal of Wuhan University of Techonlogy, 2008, 30(12)： 129-132.

本文引用格式：陳東陽，LaithK.Abbas，王國平，等. 流場環境對柔性立管濕模態的影響[J]. 哈爾濱工程大學學報， 2017， 38(10): 1587 -1594.

CHEN Dongyang, Laith K. Abbas, WANG Guoping, et al. Influence of flow environment on wet modal vibration of flexible riser[J]. Journal of Harbin Engineering University， 2017， 38(10): 1587-1594.

Influenceofflowfieldenvironmentonwetmodalvibrationofflexibleriser

CHEN Dongyang, LAITH K. Abbas, WANG Guoping, RUI Xiaoting

(Institute of Lunch Dynamics, Nanjing University of Science & Technology, Nanjing 210094, China)

To analyze the influence of static hydro-pressure and transient flow field loads on the wet modal vibration of a 3D PVC flexible riser, a wet model of the flexible riser based on an acoustic structure coupling model that considers water media and top tension was first calculated under different conditions. Good agreement between the results and the experimental data was achieved. Then, the transient flow field loads were calculated by computational fluid dynamics (CFD), which did not consider the fluid-structure coupling, and the CFD/CSD two-way coupling method, which considered the fluid structure interaction. Simulation results agreed well with the experimental data. Subsequently, the static hydro-pressure and the transient flow field loads caused by water depth were loaded to the 3D flexible riser. Then, static analysis was conducted, and wet modal simulation was performed. Calculation results show that wet modal frequency is much smaller than dry modal frequency, and the wet modal frequency increased with the increase in tension. The static hydro-pressure and the transient flow field loads can increase the wet modal frequency slightly. Moreover, the static hydro-pressure and the transient flow field loads have a stronger effect on low-order modes and no effect on high-order modes.

wet mode; acoustic-solid coupling model; vortex-induced vibration (VIV); top tension; flexible riser; transient flow field loads; turbulence model; dry mode

10.11990/jheu.201605083

http://www.cnki.net/kcms/detail/23.1390.U.20170816.1445.012.html

TB122

A

1006-7043(2017)10-1587-08

2016-05-24. < class="emphasis_bold">網絡出版日期

日期：2017-08-16.

國防基礎科研項目(B2620132013,A2620133008)；國家自然科學基金項目(11472135).

陳東陽 (1987-), 男, 博士研究生;Laith K. Abbas(1965-), 男, 教授, 博士生導師.

Laith K. Abbas, E-mail: laithabbass@yahoo.com.