基于SIFT特征的肺部非剛性配準應用研究

史明霞，張 旭，張 濤

(1.中國科學院 自動化研究所，北京 100190；2.北京中盾安全技術開發公司，北京 100048；3.中國人民解放軍總醫院胸外科，北京 100853)

基于SIFT特征的肺部非剛性配準應用研究

史明霞1，張 旭2，張 濤3

(1.中國科學院 自動化研究所，北京 100190；2.北京中盾安全技術開發公司，北京 100048；3.中國人民解放軍總醫院胸外科，北京 100853)

隨著肺癌發病率的增高和影像技術的進步，越來越多的微小肺癌(尤其是肺部磨玻璃結節)得以檢出，對于此類病變首先考慮手術治療。但肺是含氣組織，在術中會發生萎陷。巨大的體積變化導致肺內結節也隨之發生位移，術前CT確定的位置在術中無法定位。針對這一問題，在術中肺萎陷動物模型基礎上，提出了一種融合3D-SIFT特征的B樣條配準方法。該方法首先提取局部特征，篩選并匹配較好的特征點；然后依據浮動圖像與參考圖像匹配的特征點，得到浮動圖像的初始位置；最后利用控制網格對浮動圖像進行配準。經初步研究，對于不同萎陷狀態的肺部圖像，應用此方法得到了很好的配準結果。因此，融合3D-SIFT特征的B樣條配準方法適合肺部圖像配準，將來有望應用于微小肺癌的術中定位。

肺部圖像配準；圖像配準方法；3D-SIFT；非剛性配準；B樣條配準

0 引 言

我國肺癌發病率近10年呈逐年上升趨勢，平均每五個癌癥患者中就有一個罹患肺癌，已成為癌癥“第一殺手”。近年來，高分辨率CT的應用使越來越多的早期肺癌得以檢出，其中多數為直徑小于1 cm的磨玻璃密度的微小肺癌。早期肺癌的體積小，加之術中肺萎陷產生的巨大形變，導致術中無法定位，成為困擾手術的主要難題。為此，研究應用配準技術，對膨脹與系列萎陷狀態的肺進行配準，以期實現肺癌術中定位。

圖像配準技術在肺部圖像分析中已有廣泛應用，如：合并多幅掃描圖像的信息，即圖像融合[1]；或用于肺組織的運動預測[2]，匹配病人的呼氣和吸氣相圖像。但是，目前對肺在術中發生的巨大形變配準研究相對較少。

一般來講，醫學圖像的配準方法可分為基于灰度和基于特征兩大類[3-4]：前者信息量大，計算復雜度大，但受灰度的影響小[5-6]；而后者提取圖像中的特征點，只需要特征點匹配，對計算性能要求低，但其配準性能是由特征點匹配準確度以及特征點的分布決定的[7-8]。特征點提取越穩定，特征點匹配越精確，特征點分布越均勻，最終的整體配準結果越準確。對于復雜的肺部圖像配準，結合基于灰度和基于特征的方法，受到越來越多的關注[9-10]。首先，使用提取特征點的方法找到特征明顯的點，將特征點的對應位移信息作為灰度信息的約束；然后使用基于灰度的配準算法進行配準，顯著提高了配準精度。

通過SIFT(Scale Invariant Feature Transform)算法選取的特征點具有旋轉、變換、尺度不變性，對噪聲、亮度的變化等都具有較強的魯棒性，在二維圖像處理中，已經得到了很好的應用[11-12]。雖然存在一些提取三維圖像特征的算法，但并沒有真正地得到旋轉不變性的特征[13]。

在二維圖像中，為了得到方向不變性，在進行方向統計之前需要根據主方向對局部圖像進行旋轉。然而，在三維空間中，從一個向量方向旋轉到另一個方向的解不是唯一的。因此，之前的許多SIFT方法不具有旋轉不變性。Allaire等為了規避該問題，利用類似于二維的方法分別計算出旋轉方向角，但該方法需要的計算量大，并且角度直方圖的組距沒能均勻地量化。對此，Rister等提出了另一種擴展方法，使用結構張量，不僅能夠避免方向角的計算，而且能夠均勻地統計方向[14]。

針對早期肺癌的術中定位難題，對膨脹和萎陷狀態的肺展開圖像配準研究，在前述研究的基礎上，提出了一種融合3D-SIFT特征的B樣條配準方法。首先利用結構張量的特性對肺部CT圖像的特征點進行提取、篩選和匹配[15-16]，然后進行幾何形變，計算出待配準圖像的初始圖像，最后利用灰度圖B樣條配準方法[17]精細地配準肺部CT圖像。將該方法應用于自建的肺漸次萎陷動物模型，對于不同萎陷狀態的肺部圖像能夠得到很好的配準結果。

1 3D-SIFT特征點定位及特征提取

通過SIFT提取局部特征，不僅具有尺度不變性，而且具有旋轉角度不變性，對于圖像的亮度、角度具有很好的魯棒性。通過高斯濾波和下采樣構建尺度空間，計算連續兩層之間差值(高斯差分尺度空間)的極值來尋找候選關鍵點，再除去那些不穩定的具有邊緣響應的點即得到穩定的特征點。

1.1局部方向

為了能夠構造方向不變性的特性，通常需要每個特征點具有可復現的方向，一般為局部特征的主方向(直方圖中的峰值)，稱為該特征點的方向。根據此方向旋轉浮動圖像的局部數據，從而使其具有旋轉不變性。

在SIFT中，特征點的方向角度θ是由局部梯度直方圖確定的，并據此確定旋轉矩陣Rθ。然而，在高維空間中主方向的計算是復雜而不統一的。通常來說，旋轉矩陣是正交的，即|R|=1。對于N維圖像來說，旋轉矩陣可以根據N維歐拉角的三角函數確定。但N維球面坐標僅知道N-1個角度。因此，不可能由梯度直方圖確定一個向量作為特征點的方向。所以之前的很多3D-SIFT特征是不具有旋轉不變性的。

一種簡單的替代指定方向的方法是使用梯度之間的相關性，該方法具有各向同性，能夠很好地應用于任意維度，稱之為結構張量。

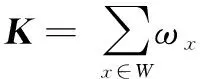
(1)

結構張量是實對稱矩陣。因此，該矩陣具有正交的特征向量分解，即K=QΛQT。如果特征值是不同且有序的，那么特征向量便是唯一的(在不考慮正負的情況下)。顯然，當對K進行旋轉時，其特征向量也同樣進行了旋轉。事實上，矩陣Q不能提供魯棒性的方向，主要由于在每個特征向量上方向是可正負的。為了解決方向上的歧義，假設Q相對于梯度是不變的，采用以圖像的局部梯度為參考方向。

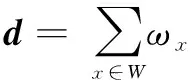
(2)

(3)

其中，qi為Q的第i列向量。并且約束每個特征向量均是正方向，那么矩陣R的列向量可表達為：ri=siqi。矩陣R記錄了圖像中每個特征點的方向。由于旋轉矩陣R的行列式必須為1，因此，如果一旦發現|R|=-1，那么將最后一個列向量乘上-1，以保持旋轉矩陣的性質。

1.2梯度直方圖

梯度直方圖用于表示在一個窗口中梯度方向的分布情況，Lowe等認為是一種魯棒的圖像表達方法[18]。在二維SIFT中，梯度方向被劃分為8個組距，每一個組距的范圍是π/4。在高維空間中，較多地將該方法拓展到N維球面坐標上，并且在每個球角度上分割相同大小的組距。然而該方法對維度大于2的圖像是有偏差的。因為對于一個球面來說，緯度較高區域與緯度較低區域，在相同區間中所包圍的面積是不同的，高緯度的面積要小于低緯度區域的面積。因此按照該方法進行分組，統計的方向是有偏差的。

梯度直方圖的組距可以視為N球面上的區域。通過原點且與梯度向量一致的射線通過的區域即為該向量所在的組。之前提出的方法所構成的平面是不均勻的。為了解決此問題，將N維球面劃分為面積、形狀相同的多邊形。且構成的凸多面體的個數滿足維度N的限制。在三維空間中，最大的正多面體是正二十面體。

采用了十二面體，通過線性插值的方法以減少量化梯度對直方圖的影響，而不是直接統計各個平面所對應的向量的多少。如圖1所示，首先找到一個梯度向量V感興趣的平面p1p2p3。之后利用線形插值方法確定該向量對該三角形的三個頂點的貢獻度λ1,λ2,λ3，將此值分別加到各對應的頂點組上。如圖1所示，這等價于12面體的每個頂點構成小三角形，且以各個頂點為重心的平面上的插值(12面體與20面體是對偶圖)。

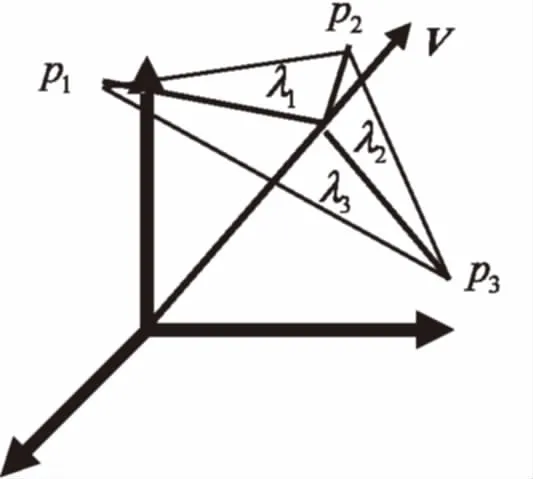
圖1 統計直方圖示例

類似于SIFT，特征描述為在不同的子區域(4×4×4)中構成的直方圖向量，且每個直方圖具有12個頂點，最終的描述符的維度為4×4×4×12=768。梯度向量對vi的貢獻度為：

f(vi)=wwinwsλi‖‖

(4)

其中，wwin為窗口的權重；ws為子區域插值的權重；λi為相對頂點vi梯度的重心坐標。

最后，對這些特征描述符進行歸一化，并清空掉小于常量δ的vi以減少噪音干擾，之后再次進行歸一化。

1.3特征點篩選

得到的點中存在較多噪聲和不穩定的點，因此需要選擇一種方法過濾特征不明顯的點。首先，考慮結構張量的特性。對于特征明顯的角點區域，其對應的結構張量矩陣的跡必須大于0。因此刪除那些小于常量β的特征點。其次，根據梯度與特征向量之間的夾角，如果兩個向量接近于垂直，那么該梯度方向是不穩定的。因此拋棄那些最小角度的余弦小于γ的關鍵點。

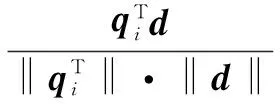
(5)

最后，判定特征向量的穩定性。拒絕接受那些特征值之間變化較大的特征點。這三個條件可以過濾掉很大一部分不穩定的特征點。

2 配準變換

3D-SIFT提取的CT圖像特征點以及特征描述符，可以利用最近鄰方法確立兩幅CT圖像特征點的對應關系。依據特征描述符之間的L2距離作為相似性度量。為了保證一致性，采用同樣的方法逆向匹配目標圖像與浮動圖像之間的特征。也就是說F1與F2匹配，有且僅有F2也與F1匹配。

(6)

使用B樣條配準算法[19-20]對浮動圖像進行非剛性變換。B樣條是具有緊支持集的基函數，其基本思想是確定控制點即可確定一個變形場，位于變形場中的圖像隨控制點的形變而變形。B樣條具有緊支持集，每個控制點只影響其局部領域，且可以得到C2光滑的連續變換。通過匹配的特征點，可以確定模板圖像位移場。

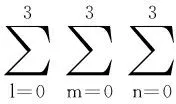
(7)

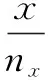
(8)

由于B樣條的計算量與控制點的個數相關，控制點越多，自由度越高，計算量就越大。因此一般采用多分辨率的B樣條來配準圖像。

由于可能存在成像因素導致的全局運動，因此利用特征點的對應關系擬合兩幅圖像之間的仿射變換，去除不同時間掃描的全局形變[21]。由于特征點匹配可能存在誤判的情況，因此使用RANSAC方法來擬合對應特征點之間的全局變換[22-23]。

肺部的萎陷過程并不是簡單的仿射變換，肺部的不同部位會發生不同的變換。如果簡單依據仿射變換后的結果對肺部進行B樣條配準容易陷入局部解中。依據特征點對應關系，將對應的特征點作為B樣條向量場的控制點，由控制點之間的相對位移便可計算出浮動圖像的位移場，進而得到浮動圖像的初始位置，而不僅是使用仿射變換作為B樣條配準的初始位置。初始的浮動圖像的位置可表示為：

x'=u(x)+x

(9)

最后，使用控制網格再次對浮動圖像進行精細配準。配準的目的是尋找變換函數φ，使浮動圖像T通過變換盡量與參考圖像R相似。一般將形變函數φ表示為一個位移函數u(x)。

φ(x)=x-u(x)

(10)

那么，該優化問題可以使用能量函數來表達。使用常用的SSD(Sum of Squared Differences)作為代價函數。

E=∑(IT(X')-IR(X))2=

∑(IT(u(x)+x)-IR(X))2

(11)

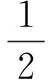
J=E+λS(u)

(12)

采用通用的變分法來解決該優化問題。該方法使用拉格朗日方程的必要條件確定該式的最小值。即尋找一條通向J(u)最小的路徑。該路徑上的每一個點都是沿著梯度的負方向移動。其對應的微分方程為：

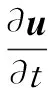
(13)

而能量函數的梯度可以表示為：

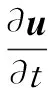
(14)

其中，f=E(u)。

該微分方程最簡單、直接的迭代求解辦法是顯式地將時間離散化。通過一個時間間隔τ在梯度方向變化得到位移的變換，按照公式更新位移。

uk+1=uk-τ(f(uk)-αλuk)

(15)

為了得到更加有效穩定的結果，增加了額外的線性搜索過程，用于確定每一次最好的時間間隔。

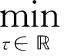
(16)

3 配準過程

首先，提取匹配浮動圖像與參考圖像之間的特征。為了能夠集中采集肺內部的特征點，在提取特征點之前，使用區域增長的方法分割出CT中的肺部區域，在分割的區域內提取圖像特征。

由圖2可知，在肺內部，特征一般存在于血管、氣管的末梢及分支處[24-25]，但這些區域有一部分并未被分割結果覆蓋，因此采取圖像的膨脹腐蝕算法使其盡量覆蓋更多的特征明顯的區域。

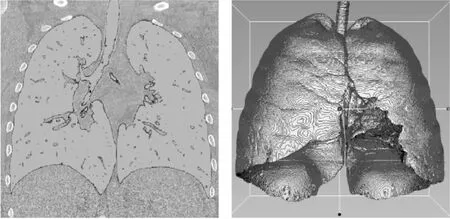
圖2 人體肺部圖像分割結果

為了提高計算效率，在被分割結果Mask覆蓋的區域處，提取3D-SIFT特征點及對應的特征描述符。圖3中的白色亮點即為檢測到的3D-SIFT特征點。由圖3可知，得到的特征點分布較為均勻，且大部分分布在特征明顯的區域。

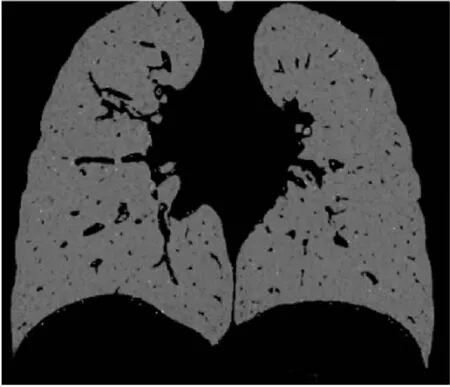
圖3 人體肺部特征點提取結果

最后，計算出浮動圖像變換到參考圖像的全局仿射矩陣。再利用特征點的對應關系采用B樣條插值的方法計算出浮動圖像的初始位置，根據此初始位置利用控制網格再次使用B樣條插值，并根據浮動圖像的控制點的位移，迭代變換浮動圖像，最終得到配準后的浮動圖像。

4 實驗及結果分析

為進行配準研究，建立了肺漸次萎陷動物模型，通過控制肺內的含氣量，模擬肺的逐步萎陷過程。采用256層螺旋CT掃描機進行全肺掃描。經多次CT掃描，獲得了肺在不同萎陷狀態下的圖像，記錄了肺從膨脹到萎陷的全過程，同時記錄了肺內大的血管、支氣管等特征結構在不同萎縮狀態下的位置及變化。CT掃描圖像清晰，輸出Dicom文件。如圖4所示，從左向右分別表示肺從完全膨脹到逐漸萎陷的狀態(標示1-4)。通過多次實驗，逐漸形成了肺漸次萎陷動物模型數據庫。

圖4 肺萎陷CT掃描圖像

然后，分割出目標圖像和浮動圖像的肺部區域。由于肺部在萎陷狀態下，有一些特征會逐漸消失，因此，在提取特征點之后，增加了一些人工標注的特征點，然后利用B樣條配準方法，得到匹配之后的圖像。肺部在各階段萎陷狀態下的配準效果如圖5所示。

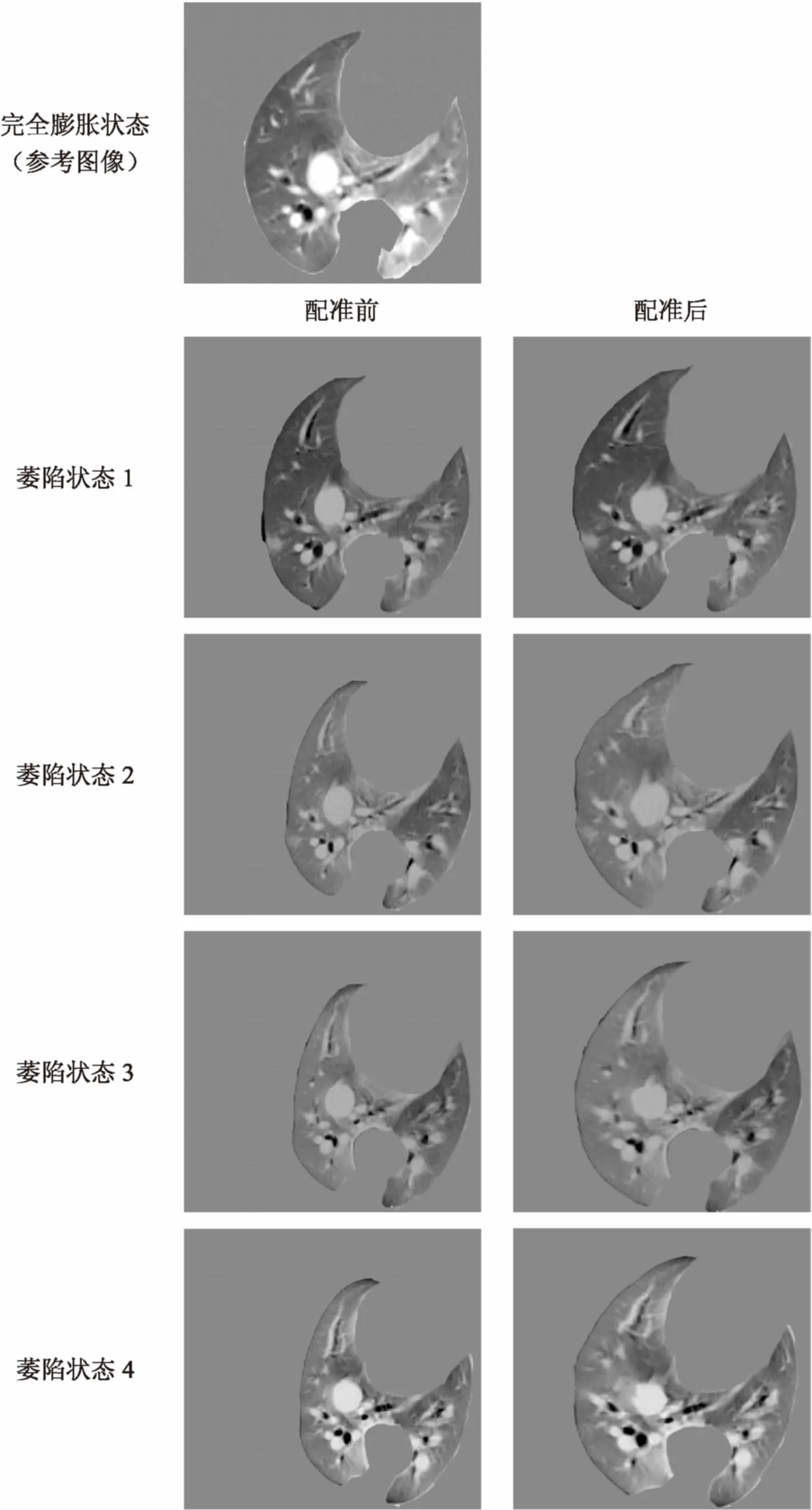
圖5 配準效果圖

5 結束語

肺癌的高發病率使其成為全社會防治重點，而術中定位卻始終困擾著肺癌的手術治療，因此，應用圖像配準技術輔助實現無創定位已成為亟待解決的問題。針對肺術中萎陷的大形變特點，采用融合3D-SIFT特征的B樣條配準方法。使用改進的3D-SIFT算法提取肺部CT圖像的局部特征，在此基礎上利用特征點對應關系計算浮動圖像的初始位置，使用B樣條插值算法對萎陷狀態下的肺部圖像進行配準。通過肺漸次萎陷動物模型的實驗證明，該方法適合肺術中萎陷過程的圖像配準，將來有望應用于微小肺癌的術中定位。但是，對于萎陷過程中肺葉發生的分裂現象等，尚需進一步研究。

[1] 余 霞,葛 紅,李 彬,等.基于并行計算和多層次B樣條的肺部CT-PET圖像配準[J].計算機應用,2009,29(7):1940-1942.

[2] Ehrhardt J,Werner R,Schmidt-Richberg A,et al.Statistical modeling of 4D respiratory lung motion using diffeomorphic image registration[J].IEEE Transactions on Medical Imaging,2011,30(2):251-265.

[3] 楊 健,李若楠,黃晨陽,等.基于局部顯著邊緣特征的快速圖像配準算法[J].計算機應用,2014,34(1):149-153.

[4] 夏 威,高 欣,王 雷,等.基于點集與互信息的肺部CT圖像三維彈性配準算法[J].江蘇大學學報:自然科學版,2014,35(5):558-563.

[5] 王建文,李 青.基于點和邊緣相結合特征提取的圖像配準算法[J].計算機工程與設計,2009,30(4):928-930.

[6] Huang X,Paragios N,Metaxas D N.Shape registration in implicit spaces using information theory and free form deformations[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2006,28(8):1303-1318.

[7] Glaunes J,Qiu A,Miller M I,et al.Large deformation diffeomorphic metric curve mapping[J].International Journal of Computer Vision,2008,80(3):317-336.

[8] Castillo R,Castillo E,Guerra R,et al.A framework for evaluation of deformable image registration spatial accuracy using large landmark point sets[J].Physics in Medicine & Biology,2009,54(7):1849-1870.

[9] Yin Y,Hoffman E A,Ding K,et al.A cubic B-spline-based hybrid registration of lung CT images for a dynamic airway geometric model with large deformation[J].Physics in Medicine & Biology,2011,56(1):203-218.

[10] Cao K,Ding K,Reinhardt J M,et al.Improving intensity-based Lung CT registration accuracy utilizing vascular information[J].International Journal of Biomedical Imaging,2012,2012:285136.

[11] Candemir S,Jaeger S,Palaniappan K,et al.Lung segmentation in chest radiographs using anatomical atlases with nonrigid registration[J].IEEE Transactions on Medical Imaging,2014,33(2):577-590.

[12] Gong M,Zhao S,Jiao L,et al.A novel coarse-to-fine scheme for automatic image registration based on SIFT and mutual information[J].IEEE Transactions on Geoscience & Remote Sensing,2014,52(7):4328-4338.

[13] Goncalves H,Corte-Real L,Goncalves J.Automatic image registration through image segmentation and SIFT[J].IEEE Transactions on Geoscience & Remote Sensing,2011,49(7):2589-2600.

[14] Rister B,Reiter D,Zhang H,et al.Scale-and orientation-invariant keypoints in higher-dimensional data[C]//IEEE international conference on image processing.[s.l.]:IEEE,2015:3490-3494.

[15] Holden M.A review of geometric transformations for nonrigid body registration[J].IEEE Transactions on Medical Imaging,2008,27(1):111-128.

[16] Mattes D,Haynor D R,Vesselle H,et al.PET-CT image registration in the chest using free-form deformations[J].IEEE Transactions on Medical Imaging,2003,22(1):120-128.

[17] Yin Y，Hoffman E A，Lin C L.Mass preserving non-rigid registration of CT lung images using cubic B-spline[J].Medical Physics,2009,36(9):4213-4222.

[18] Lowe D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.

[19] 馮兆美,黨 軍,崔崤峣,等.基于B樣條自由形變三維醫學圖像非剛性配準研究[J].影像科學與光化學,2014,32(2):200-208.

[20] Xie Z,Farin G E.Image registration using hierarchical B-splines[J].IEEE Transactions on Visualization & Computer Graphics,2004,10(1):85-94.

[21] 羅文超,劉國棟,楊海燕.SIFT和改進的RANSAC算法在圖像配準中的應用[J].計算機工程與應用,2013,49(15):147-149.

[22] 常 青,張 斌,邵金玲.基于SIFT和RANSAC的特征圖像匹配方法[J].華東理工大學學報:自然科學版,2012,38(6):747-751.

[23] 馬麗麗,曹春梅,陳金廣,等.基于RANSAC的特征點匹配算法[J].計算機工程與設計,2016,37(7):1794-1797.

[24] Bauer C,Krueger M A,Lamm W J,et al.Airway tree segmentation in serial block-face cryomicrotome images of rat lungs[J].IEEE Transactions on Bio-medical Engineering,2014,61(1):119-130.

[25] Dhara A K,Mukhopadhyay S,Dutta A,et al.A combination of shape and texture features for classification of pulmonary nodules in lung CT images[J].Journal of Digital Imaging,2016,29(4):466-475.

ResearchonApplicationofPulmonaryNon-rigidRegistrationMethodwith3D-SIFTFeatures

SHI Ming-xia1，ZHANG Xu2，ZHANG Tao3

(1.Institute of Automation，Chinese Academy of Sciences，Beijing 100190，China;2.Beijing Zhongdun Security Technology Development Co,Beijing 100048,China;3.Department of Thoracic Surgery，Chinese PLA General Hospital,Beijing 100853,China)

With the increased incidence of lung cancer and the progress of medical imaging technology，more and more small pulmonary nodules (especially for ground glass nodules) have been detected.Surgical treatment is the first consideration for such nodules.But lung is a gas containing organ,which will collapse during operation.With the huge volume change,pulmonary nodule will change its position,which makes location difficult in the operation.To solve it,an animal model database simulating lung collapse in operation is established.A B-spline curves registration method with fusion of 3D-SIFT features is proposed.Local feature is extracted firstly,and then the feature points are selected and matched.According to the feature points the initial position of the floating image is obtained.Used the control grid,the floating image is registered finally.For a series of lung CT images in different collapse states,satisfactory registration results are obtained by it which is suitable for pulmonary images registration and can be used for intraoperative localization of small pulmonary nodules in the future.

pulmonary images registration;registration methods;3D-SIFT;non-rigid registration;B-spline based registration

2016-09-25

2016-12-28 < class="emphasis_bold">網絡出版時間

時間：2017-07-19

北京市自然科學基金項目(7142152)

史明霞(1980-)，女，碩士，高級工程師，研究方向為計算機視覺；張 濤，博士，通信作者，研究方向為早期肺癌的計算機輔助外科。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170719.1108.014.html

TP391.9；R318.04

A

1673-629X(2017)11-0181-06

10.3969/j.issn.1673-629X.2017.11.039