酸壓裂縫中酸液微觀流動數值模擬及分析

劉享 ， 伊向藝 ，2， 吳元琴 ， 李沁

（1.成都理工大學能源學院，成都610059；2.油氣藏地質及開發工程國家重點實驗室，成都610059）

酸壓裂縫中酸液微觀流動數值模擬及分析

劉享1， 伊向藝1，2， 吳元琴1， 李沁1

（1.成都理工大學能源學院，成都610059；2.油氣藏地質及開發工程國家重點實驗室，成都610059）

酸壓是儲層增產的重要措施，搞清楚酸液在裂縫中的流動規律對酸壓改造具有重要意義。前人的研究主要是通過物理實驗來研究酸壓裂縫中的酸液流動，所采用的裂縫模型與實際的裂縫有較大差別，很少考慮到裂縫的粗糙度對酸液流動的影響。因此，利用數值模擬方法，借助于fluent軟件模擬了裂縫中酸液的流動，分析了裂縫壁面粗糙度對酸液流動的影響。實驗結果表明：單相流和兩相流在水平中軸線上流速曲線都呈現“廠”字形，在垂直中軸線上流速曲線呈現“幾”字形，在單相流中，波峰處流速明顯大于其他部位的流速，中軸線上的流速反而較小，相反在兩相流中，中軸線上的流速是最大的；隨著粗糙度的增加，酸液的驅替長度增加；在同一粗糙度下驅替長度與黏度比M并不成線性關系，當M等于6時，4種粗糙度下的酸液驅替長度都達到最小，當M小于6時，驅替長度隨黏度比增加而減小，M大于6時，驅替長度又隨黏度比的增加而增加，其中粗糙度λ = 0.1、0.2、0.3時，在8＜M＜11之間黏度比對酸液的驅替長度影響相對較小。酸液驅替長度的增加可以增加酸蝕作用距離，形成酸蝕溝槽，從而增加裂縫的導流能力，達到酸壓改造目的，在考慮到施工和成本的條件下，應該使前置液和酸液的黏度避開下降段和平臺段的黏度值。

酸液流動；fluent模擬；VOF模型；粗糙度；黏度比

0 引言

酸壓結合了水力壓裂和酸化的優點，成為低滲透油氣藏，特別是低滲透碳酸鹽巖油氣藏主要的增產措施。從目前的發展狀況和技術特點看，酸壓可以分為常規酸壓和深度酸壓2大類別。酸壓過程中，前置液壓開并進入裂縫，降低裂縫壁面的溫度，并在裂縫壁面形成濾餅，降低后續酸液的濾失量；后續酸液的黏度遠小于前置液的黏度，流動過程形成黏性指進。縫內酸液指進會改變酸液的流動分布狀況，進而影響酸巖反應，最終改變酸蝕縫長和酸蝕裂縫導流能力。Hele和Shaw首次使用Hele-Shaw Cell進行了平行板間黏性流動模擬，拉開了裂縫中流體流動物理模擬研究的序幕[1]。Davies等人采用透明樹脂平板模型進行模擬，他們在模擬中考慮了注液流量、裂縫寬度、注孔間距對流動形態的影響[2]。李小剛，楊兆中等人采用大理石板和雙層鋼化玻璃板構成裂縫壁面，使用真實鹽酸進行了模擬實驗，分析了酸巖反應和酸液自身重力綜合影響下的酸液行為[3]。

前人的研究主要是通過物理實驗來研究酸壓裂縫中的酸液流動，所采用的裂縫模型與實際的裂縫有較大差別，很少考慮到裂縫的粗糙度對酸液流動的影響。因此，利用數值模擬方法，借助于FLUENT軟件模擬了裂縫中酸液的流動，并分析了裂縫壁面粗糙度對酸液流動的影響[4-15]。

1 幾何模型建立

為了研究方便，選取了裂縫的一段，只考慮平面二維裂縫形態，因此忽略重力的影響。將粗糙的裂縫面簡化為圖1所示的二維幾何模型。

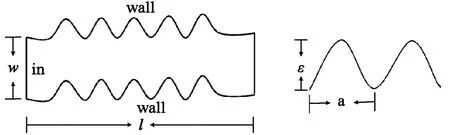
圖1 裂縫二維幾何模型

在幾何模型中，w為裂縫寬度，l為裂縫模擬長度，ε為粗糙單元高度。相對粗糙度λ定義為粗糙單元高度ε與通道寬度w的比值，即

2 數值模擬理論與方法

2.1 VOF模型

在FLUENT中，共有3種歐拉-歐拉多相流模型，即VOF（Volume of Fluid）模型、歐拉（Eulerian）模型和混合物（Mixture）模型。其中VOF模型是一種在固定歐拉網格下的表面跟蹤方法，該模型可以得到一種或多種互不相融流體間的交界面。在VOF模型中，不同的流體組分共用一套動量方程，計算時在全場的每一個計算單元內，都記錄下各流體組分所占有的體積率。

Hirt和Nichols（1981年）[4]率先提出VOF方法，其基本思想是通過構造流體體積函數F來捕捉自由面界面的運動變化。F=1，表示網格中充滿流體；F=0表示沒有流體；0＜F＜1為含有自由面。所以，只要求出值，就可以使用界面重構技術構造出近似界面，從而將界面追蹤轉變為計算值的問題。

相函數輸運方程為:

展開可得到：

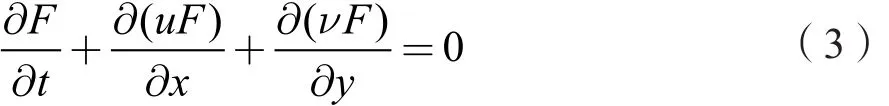
目前，常用的數值離散方法主要有有限差分法、有限元法和有限容積法。其中，有限容積法是先將求解域劃分為一系列不重復的控制體積，再將微分方程對每一個控制體積分，從而得到一組離散方程。相比其他離散方法它具有不可替代的優勢：（1）具有良好的積分守恒性，在整個計算區域都是守恒的，所以即使在較粗網格中也能獲得很好的結果；（2）計算過程穩定性好，在計算網格不變的情況下，適當加大時間步長，只影響精度，不影響計算過程的收斂性，便于程序的調試。

根據所研究的對象，擬采用ICEM CFD對裂縫通道進行非結構化網格劃分，確保網格的質量，采用PISO算法進行求解。

2.2 控制方程

VOF模型采用標準湍流模型的方程，其基本控制方程由以下各式組成。質量守恒方程：

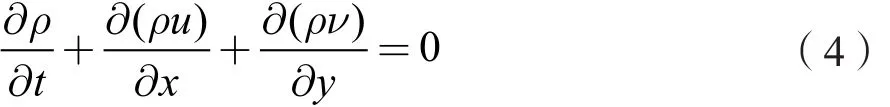
對于二維不可壓縮流體連續性方程為：

動量守恒方程：

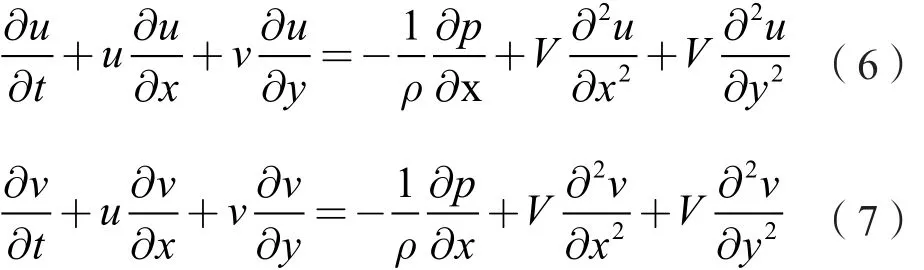
式中，ρ為密度，kg/m3；t為時間，s；u、v為速度，m/s；p為壓強，Pa。

湍流動能及其耗散率，從以下方程式獲得，湍流動能方程k。

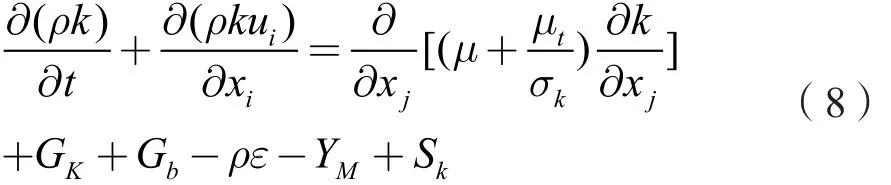
擴散方程e：

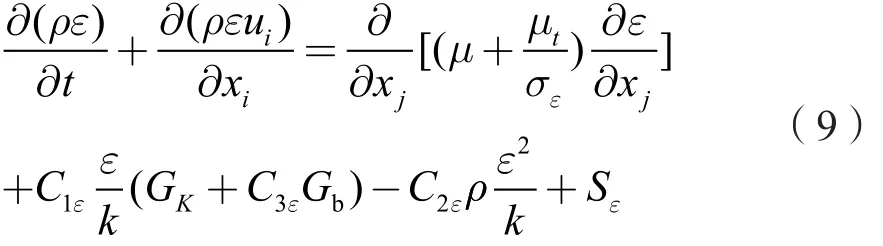
式中，μ為動力黏性系數；Gk為表示由于平均速度梯度引起的湍流動能k的產生項；Gb為由于浮力影響引起的湍流動能k的產生項；YM為可壓縮湍流脈動膨脹對總的耗散率的影響 ；C1ε、C2ε、C3ε為經驗常數 ；Sε、Sk為用戶定義的源項 ；σk、σε為 k方程和e方程的湍流Prandtl數。湍流黏性系數μt可以寫成k和ε的函數，Cμ為經驗常數，取0.09，如下。

在FLUENT中，作為默認值常數，C1ε=1.44，C2ε=1.92，湍流動能k與耗散率ε的湍流普朗特數分別為 σk=1.0，σε=1.3。

2.3 邊界條件

按照實際情況，確定如下的邊界條件。入口端設為速度入口，邊界條件為：

出口為壓力出口，邊界條件為：

上下表面為絕熱邊界，因此有：

3 模擬與分析

3.1 模型假設

（1）整個區域為剛性區域，無變形；（2）流體不可壓縮；（3）不考慮重力影響。

3.2 模擬初始條件及參數設置

模擬過程：初始狀態下，裂縫中充滿前置液，酸液從進口以一定的流速進入裂縫，模擬一段時間后酸液在裂縫中的流動形態。根據模擬的情況，設置的初始參數如表1所示。

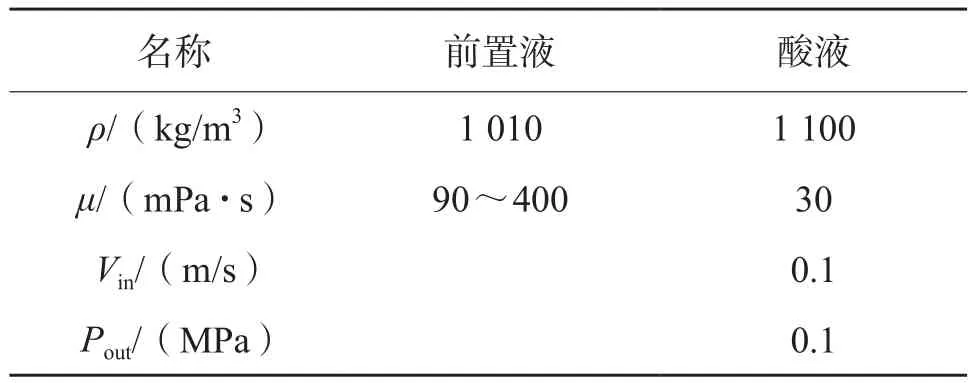
表1 模擬初始參數

3.3 結果及分析

3.3.1 兩相流與單相流的區別

模擬了裂縫中單相流和多相流的流動形態。其中相對粗糙度λ=0.1，入口速度為0.1 m/s，出口壓力為0.1 MPa。圖2是模擬的速度云圖。

圖3顯示的是裂縫中單相流和多相流的速度云圖，圖中的顏色深淺代表速度的大小，明顯可以看出2者的速度分布存在差異。在單相流中，波峰處流速明顯大于其他部位的流速，中軸線上的流速反而要小。相反在兩相流中，中軸線上的流速是最大的。但2種流動的波谷處，流速都比較小。為了分析流速的分布規律，選取了水平中軸線和垂直中軸線流速為研究對象，通過FLUENT后處理獲得這2條線上的流速分布情況（圖3）。

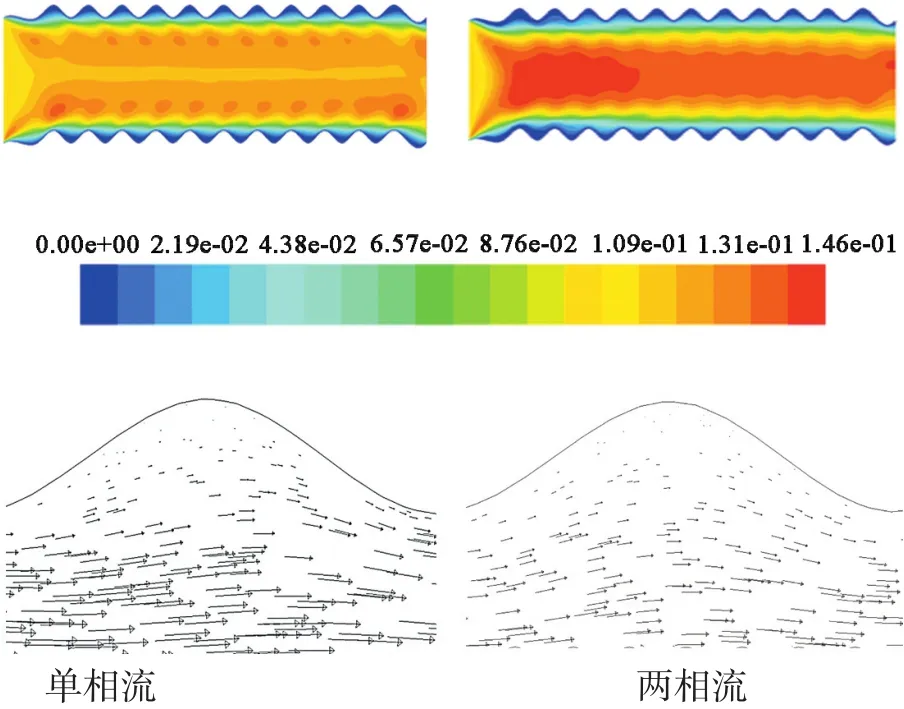
圖2 速度云圖以及速度矢量圖

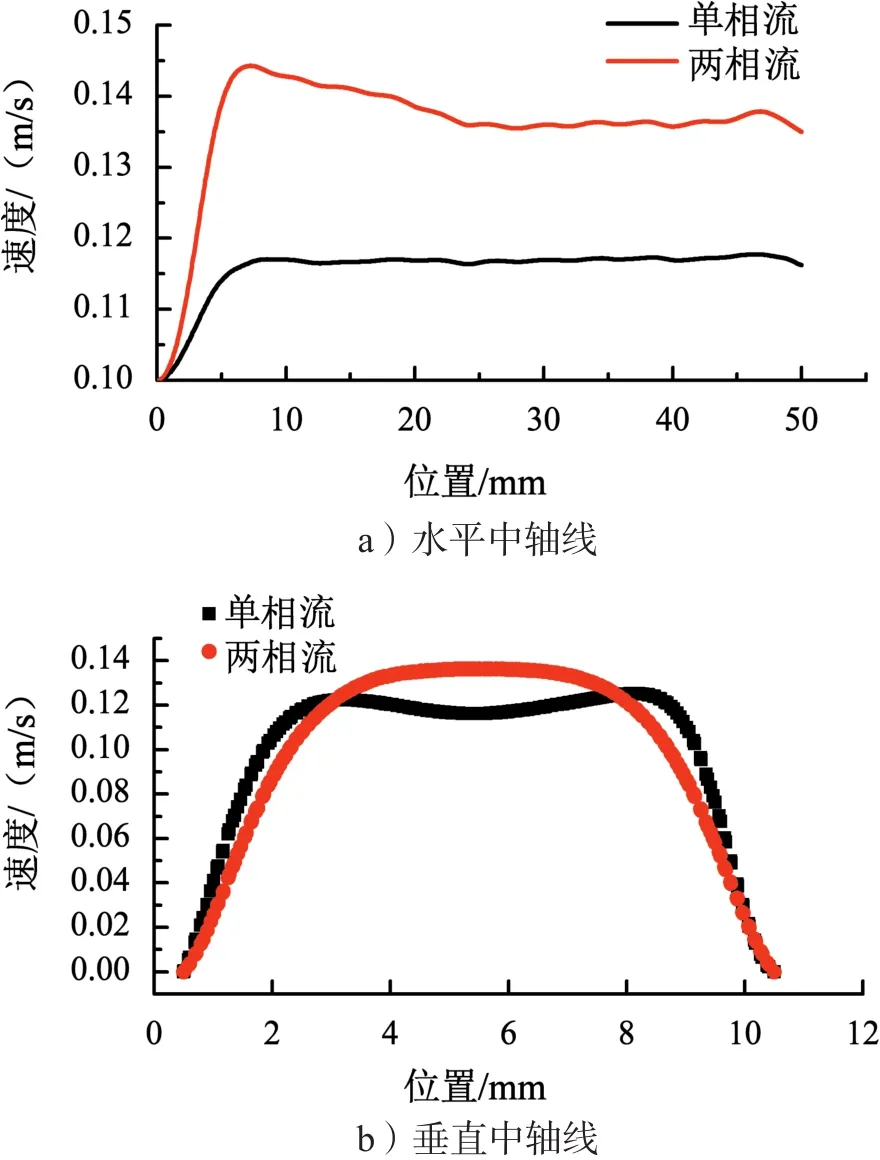
圖3 水平中軸線和垂直中軸線上速度曲線

在水平中軸線上2種流動方式流速曲線都呈現“廠”字形。在0～10 mm之間流速迅速上升，之后流速的變化相對較小。但是，兩相流動水平中軸線上的流速始終大于單相流，這與速度云圖的分析結果是一致的。在10～50 mm之間，單相流水平中軸線上的流速幾乎不變，而兩相流中流速先是下降，接著維持流速不變。在垂直中軸線上2種流速曲線呈現“幾”字形。由曲線可以發現在壁面附近流速的變化較快，說明壁面的形態對附近的流體有重要的影響。而遠離壁面的地方，流速的變化相對較小。兩相流中越靠近中軸線，流速越大。

3.3.2 相對粗糙度的影響

在模擬裂縫粗糙度對酸液流動影響時，設置了4種不同粗糙度（λ=0.1、0.2、0.3、0.4）的裂縫面。酸液的入口速度為0.1 m/s，黏度為30 mPa·s，前置液的黏度為300 mPa·s。整個計算過程進行了0.2 s，計算步長設置為0.002 s。模擬結果的相態變化見圖4，其中紅色部分為酸液，藍色部分為前置液。

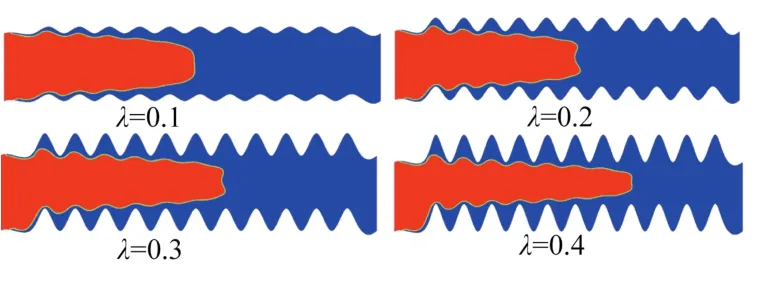
圖4 不同粗糙度下酸液流動相態圖

不同粗糙度下酸液在裂縫中的分布不同，λ為0.1、0.2、0.3、0.4時，驅替長度分別為25.328 5、26.926 9、29.904 3、34.145 9 mm，隨著粗糙度的增加，酸液的驅替長度增加。酸液驅替長度的增加可以增加酸蝕作用距離，形成酸蝕溝槽，從而增加裂縫的導流能力，達到酸壓改造目的。

圖5 a）反映了在水平中軸線上（x=0～50 mm，y=5 mm）速度以及沿程壓力情況。4種粗糙度下，速度曲線都呈現“廠”字形，在0～10 mm段，速度上升較快，且粗糙度越大酸液的流動速度越大。在0～50 mm段，可以明顯看出隨著粗糙度的增加曲線的波動也就越大。裂縫的延伸軌跡并不是一條直線，而且裂縫表面也不是光滑的，因此，裂縫面的形狀會對酸液流動產生影響，而且粗糙度越大，它對酸液流動的擾動也就越大。

圖5 b）為不同粗糙度下壓力與位置的關系圖，壓力下降分為2個階段，前一階段下降慢，后一階段下降快；粗糙度越大壓力也越大，而且進口壓力隨粗糙度的增加而增加，粗糙度越大沿程的壓降也越大（表2）。

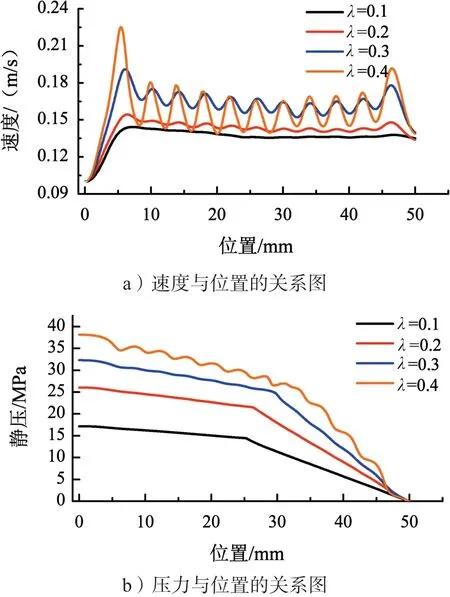
圖5 不同粗糙度下速度和壓力與位置的關系圖（x=0～50 mm，y=5 mm）

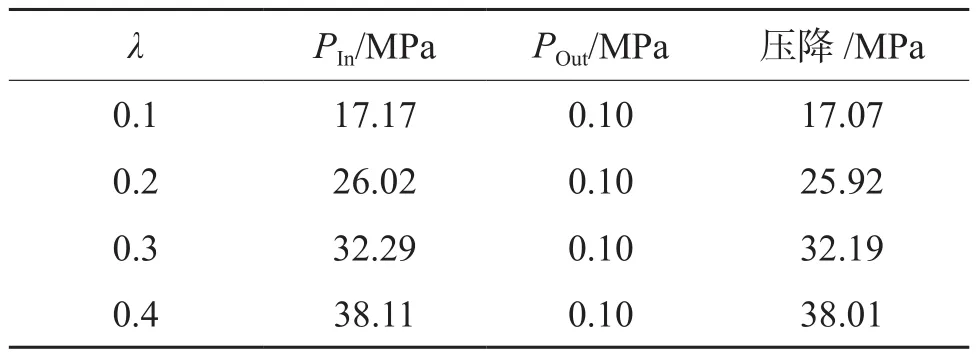
表2 不同粗糙度下進出口壓力以及壓降（x=0～50 mm，y=5 mm）

3.3.3 不同黏度的影響

保持酸液的黏度比不變（30 mPa·s），通過改變前置液的黏度來獲得流體間不同的黏度比M。圖6分別給出了各粗糙度不同，黏度比M=3、4、6、8、9、10、11、12、13、14、16下的酸液驅替長度。觀察7圖可以發現，粗糙度越大，酸液的驅替長度越大；但在同一粗糙度下驅替長度與黏度比并不成線性關系，當M=6時，4種粗糙度下的酸液驅替長度都達到最小，當M＜6時，驅替長度隨黏度比增加而減小，M＞6時，驅替長度又隨黏度比的增加而增加，其中λ=0.1、0.2、0.3時，在8＜M＜11之間出現驅替長度隨黏度比的增加而緩慢上升，說明此時黏度比對酸液的驅替長度影響相對較小。因此，在考慮到施工條件和成本的前提下，應該使前置液和酸液的黏度比避開下降段和緩慢上升段。

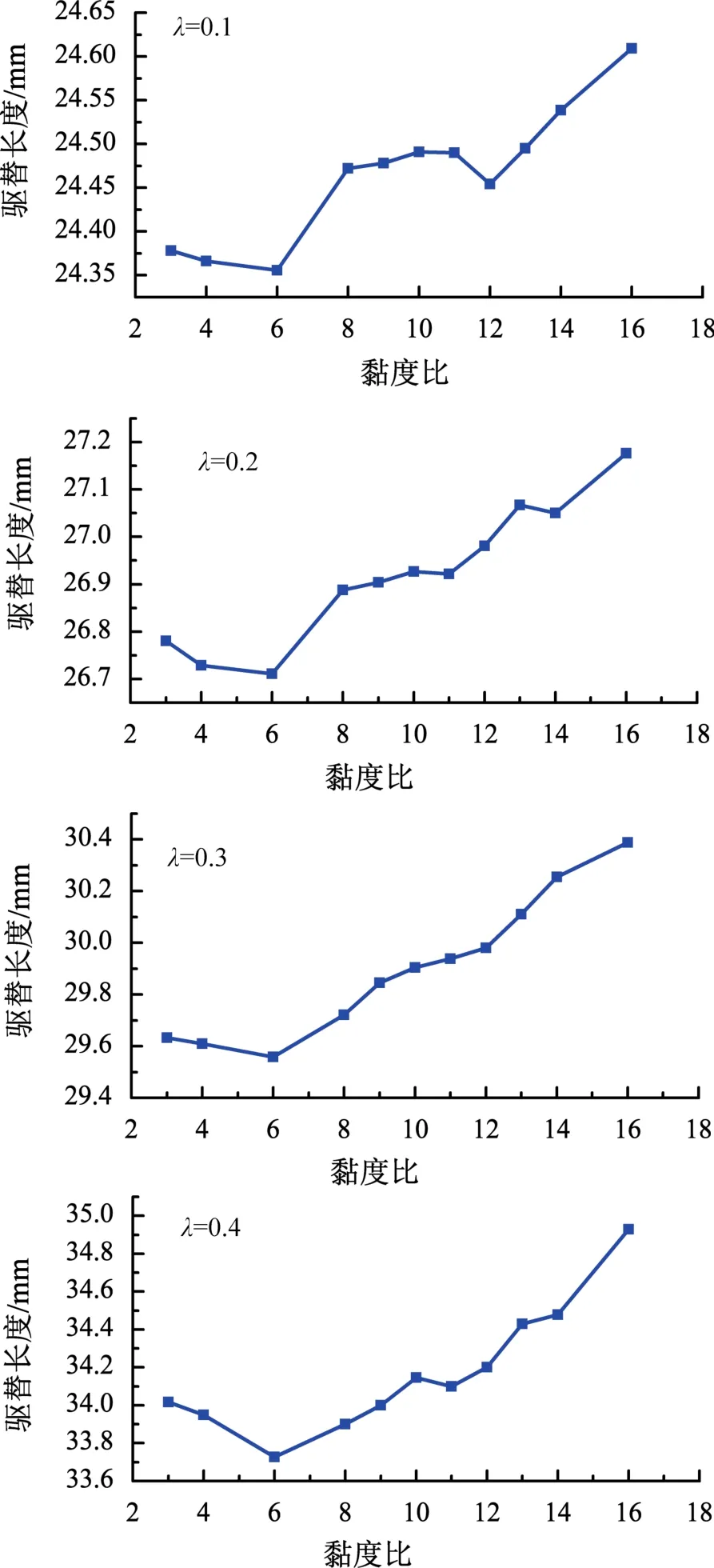
圖6 不同黏度比下酸液驅替長度

4 結論

1.單相流和多相流的速度存在明顯差異，在水平中軸線上2種流動方式流速曲線都呈現“廠”字型，在垂直中軸線上2種流速曲線呈現“幾”字形。壁面的形態對附近的流體有重要的影響，遠離壁面的地方，流速的變化相對較小。

2.不同粗糙度下酸液在裂縫中的分布不同，隨著粗糙度的增加，酸液的驅替長度增加。酸液驅替長度的增加可以增加酸蝕作用距離，形成酸蝕溝槽，從而增加裂縫的導流能力，達到酸壓改造目的。

3.在同一粗糙度下驅替長度與黏度比并不成線性關系，當M=6時，4種粗糙度下的酸液驅替長度都達到最小。當M＜6時，驅替長度隨黏度比增加而減小，M＞6時，驅替長度又隨黏度比的增加而增加，其中λ=0.1、0.2、0.3時，在8＜M＜11之間黏度比對酸液的驅替長度影響相對較小。

[1]胡江平.Hele-Shaw模型及多孔介質中兩相驅替的數值模擬研究[D].中國科學技術大學，2015．HU Jiangping. Hele-Shaw model and numerical simulation of two-phase flooding in porous media [D].China University of Science and Technology，2015.

[2]DAVIES D R， BOSMA M G R， DE VRIES W.Development of field design rules for viscous fingering in acid fracturing treatments: a large-scale model study[C]//Middle East Oil Show. Society of Petroleum Engineers，1987.

[3]李小剛，楊兆中，陳銳，等.前置液酸壓縫中酸液指進的物模與分形研究[J].西南石油大學學報，2007，29（6）：105-108.LI Xiaogang，YANG Zhaozhong，CHEN Rui，et al. Study on the model and fractal of the acid in the pre-liquid acid pressure slit[J].Journal of Southwest Petroleum University(Natural Science Edition)，2007，29（6）：105-108.

[4]HIRT C W，NICHOLS B D. Volume of fluid (VOF)method for the dynamics of free boundaries[J].Journal Of Computational Physics，1981，39（1）：201-225.

[5]譚思超，趙富龍，李少丹，等.VOF模型界面傳質與體積傳質的轉換方法[J].哈爾濱工程大學學報，2015，36（3）：317-321.TAN Sichao，ZHAO Fulong，LI Shaodan，et al.Conversion method of mass transfer and mass transfer in VOF model[J]. Journal of Harbin Engineering University，2015，36（3）：317-321.

[6] 王志東，汪德爟.VOF方法中自由液面重構的方法研究 [J].水動力學研究與進展 (A 輯 )，2003，18（1）：52-56.WANG Zhidong，WANG Deqing. Study on free liquid surface reconstruction in VOF method[J]. Hyday Research and Progress (A series)，2003，18（1）：52-56.

[7]何安定，鹿院衛，李斌，等.兩相流動中自由界面的數值模擬[J].油氣儲運，2000，19(10)：15-18.HE Anding，LU Yuanwei，LI Bin，et al. Numerical simulation of free interface in two-phase flow[J]. Oil &Gas Storage and Transportation，2000，19（10）：15-18.

[8]曹平，羅磊，劉濤影，等.巖石節理面粗糙度的分形效應與試件尺寸影響分析[J].科技導報，2011，12（24）：57-61.CAO Ping，LUO Lei，LIU Taoying，et al. Fractal effect of specimen joint roughness and analysis of specimen size[J].Science and Technology Review，2011，12（24）：57-61.

[9]張程賓，陳永平，施明恒，等.表面粗糙度的分形特征及其對微通道內層流流動的影響[J].物理學報，2009，58（10）：7050-7056.ZHANG Chengbin，CHEN Yongping，SHI Mingheng，et al. Fractal characteristics of surface roughness and its influence on laminar flow in microchannels[J].Acta Physica Sinica，2009，58（10）：7050-7056.

[10]鄒江，彭曉峰，顏維謀.壁面粗糙度對通道流動特性的影響[J].化工學報，2008，59（01）：25-32.ZOU Jiang，PENG Xiaofeng，YAN Weimou. Effects of wall roughness on channel flow characteristics[J]. Acta Chimica Sinica，2008，59（01）：25-32.

[11]王佳男.微通道中液液兩相流動與混合過程的數值模擬[D].浙江大學，2013.WANG Jianan. Numerical simulation of liquid-liquid two-phase flow and mixing process in microchannels[D].Zhejiang University，2013.

[12]楊兵，高福平.單向流作用下近壁面管道流向渦激振動[C]//第九屆全國水動力學學術會議暨第二十二屆全國水動力學研討會論文集，2009.YANG Bing，GAO Fuping. Study on vortex-induced vibration of near-wall pipelines under unidirectional flow[C]//Proceedings of the Ninth National Conference on Hydrodynamics and the Twenty-second National Symposium on Hydrodynamics，2009.

[13]呂建華，李品，劉繼東，等.水力學聚焦微通道中氣液兩相流動的數值模擬[J].化工學報，2015，66（9）：3398-3404.LYU Jianhua，LI Pin，LIU Jidong，et al.Numerical simulation of gas-liquid two-phase flow in hydraulically focused microchannels[J].Acta Chimica Sinica，2015，66（9）：3398-3404.

[14]李小剛，楊兆中，胡學明，等.酸壓裂縫中酸液流動反應行為研究綜述[J].鉆井液與完井液，2008，25(6): 70-73.LI Xiaogang，YANG Zhaozhong，HU Xueming，et al.Study on acid flow reaction behavior in acid fractures[J].Drilling Fluid & Completion Fluid，2008，25（6）：70-73.

[15]王琳琳，胡洪萍，田輝.分支型微通道水-油兩相流數值模擬[J].西安工業大學學報，2015，35（1）：45-51.WANG Linlin，HU Hongping，TIAN Hui. Numerical simulation of branch-type microchannel water - oil twophase flow[J]. Journal of Xi'an Technological University，2015，35（1）：45-51.

Numerical Simulation and Analysis of Micro Flow of Acids in Fractures Generated in Acid Fracturing

LIU Xiang1, Yi Xiangyi1,2, WU Yuanqin1, LI Qin1
(1. College of Energy Resources, Chengdu University of Technology, Chengdu, Sichuan 610059;2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, Sichuan 610059)

Acid fracturing is an important stimulation measure used in enhancing oil recovery. The understanding of flow of acids in fractures generated in reservoir fracturing is of great importance. Physical experiments have been conducted previously in the study of acid flow in fractures, and the fracture model used in the experiments are quite different than the actual fractures generated in acid fracturing, the effects of the roughness of the surfaces of fractures on acid flow are seldom considered. This paper introduces the use of a software Fluent to numerically simulate acid flow in fractures, and analyzes the effects of the roughness of the surfaces of fractures on acid flow. Experimental results showed that the flow rate curves of both single-phase flow and two-phase flow along the horizontal central axis demonstrated a shape of “廠”, while along the vertical central axis, the curve showed a shape of “幾”. In single-phase flow,flow rates around wave crest were much greater than the flow rates in other area, and the flow rate along the central axes were low.On the other hand, in two-phase flow, highest flow rates were found along central axes. With an increase in roughness of the surfaces of fractures, the length of flow of acid is extended. At the same roughness, the flow length of acid and acid viscosity are not in linear relationship. When M = 6, the flow lengths of acid in fractures with 4 different surface roughness all are the shortest. When M ＜ 6, the flow lengths decrease with increase in viscosity ratio. When M ＞ 6, the flow lengths increase with increase in viscosity ratio. A plateau appears with M between 8 and 11, meaning that the effects of viscosity ratio on acid flow length are becoming weak. Increase in acid flow length increases the length of acid erosion, forms more cannelures, thereby enhancing the flow conductivity of fractures andfulfilling the purpose of acid fracturing. Taking into account operation cost, in selecting prepad fluid and acid, viscosities corresponding to the values around the descending section and the plateau section of the flow rate curve, should not be used.

Acid flow; Simulate with Fluent; VOF model; Roughness; Viscosity ratio

劉享，伊向藝，吳元琴，等.酸壓裂縫中酸液微觀流動數值模擬及分析[J].鉆井液與完井液，2017， 34（4）：106-111.

LIU Xiang，YI Xiangyi，WU Yuanqin，et al.Numerical simulation and analysis of micro flow of acids in fractures generated in acid fracturing[J].Drilling Fluid & Completion Fluid，2017， 34（4）：106-111.

TE357.12

A

1001-5620（2017）04-0106-06

10.3969/j.issn.1001-5620.2017.04.020

國家自然科學基金青年基金“碳酸鹽巖儲層酸巖反應表面形態與演化”（51504200）。

劉享，1991年生，在讀碩士研究生，研究方向為儲層保護與儲層改造。電話 18208182201；E-mail：1119579833 @qq.com。

2017-4-5；HGF=1704F8；編輯 付玥穎）