基于相位相關的部分可辨編隊精細起始算法

王聰， 王海鵬， 熊偉， 何友

1.海軍航空工程學院 信息融合技術研究所， 煙臺 264001

2.飛行器測控與通信教育部重點實驗室， 重慶 400044

基于相位相關的部分可辨編隊精細起始算法

王聰1,2,*， 王海鵬1， 熊偉1， 何友1

1.海軍航空工程學院 信息融合技術研究所， 煙臺 264001

2.飛行器測控與通信教育部重點實驗室， 重慶 400044

針對部分可辨條件下編隊目標的精細起始難題，提出了一種基于相位相關的部分可辨編隊精細起始算法。首先，采用基于坐標映射距離差分的快速群分割與基于編隊中心點的預互聯對雷達量測進行預處理；然后，利用圖像匹配中相位相關特性，將相鄰時刻編隊結構進行補償對準，解決了低目標發現概率情況下的編隊結構對準問題；最后，采用增加虛擬量測并后驗判決的方式，結合最近鄰法做編隊航跡精細互聯，在填補航跡缺失、增加正確航跡的同時抑制虛假航跡的產生。經仿真驗證，與修正的邏輯法、基于相對位置矢量的灰色編隊精細起始算法相比，本文所提算法在提高航跡正確起始率、抑制虛假航跡方面性能優勢顯著，且對環境雜波與雷達精度具有較好的魯棒性，對目標發現概率具有較好的適應性。

部分可辨； 航跡起始； 編隊目標； 相位相關； 圖像匹配

在現代戰爭中，因為特定戰術目的或其他不可控因素，特性接近的多個低可觀測目標經常會在較小的空域內構成一個復雜的目標群，如空間飛行器爆炸后產生的空間碎片群、為實現突防目的的隱身飛機編隊或中段彈道導彈飛行過程中釋放的彈頭和大量誘餌等，這些目標空域分布范圍較小，運動特征差異不明顯，且相對運動速度較低，可統稱為低可觀測編隊目標[1]。為了有效打擊敵方彈道導彈、隱身飛機和衛星等低可觀測軍用目標，要求探測系統能夠對其進行遠距離發現、跟蹤、捕獲和截擊，而傳統的多源跟蹤算法無法滿足作戰需求。因此，對低可觀測編隊目標的跟蹤問題已成為一個亟待解決的關鍵問題，對國防安全具有深遠的意義。

由于受制于測量設備角度分辨力、距離分辨力、威力及測量精度等因素，探測系統在編隊目標跟蹤過程中，通常會出現3種情況：① 探測系統完全不能分辨編隊內目標，此時編隊不可辨；② 探測系統有時能分辨編隊內目標，但又無法穩定獲取連續有效測量，屬于低可觀測編隊，此時編隊部分可辨；③ 探測系統能夠完全分辨編隊內目標，此時編隊可辨。以前由于雷達性能有限，編隊目標大多是不可辨的，因而通常基于編隊整體進行跟蹤研究。近年來，隨著雷達性能尤其是分辨率的提高，越來越多的學者開始關注如何利用部分可辨時獲得的信息改善編隊目標的跟蹤性能。

現有的編隊起始算法主要集中在編隊不可辨條件以及完全可辨條件下的。應對不可辨條件的算法有K方法[2]、集群引晶[3]、圖解法[4]以及基于Hough變換的多種引申算法[5-7]，該類算法的主要思路是將編隊目標看作一個整體進行起始，簡單易行，編隊整體的獲取概率高，但由于不能精確取得編隊內目標的個數、戰術隊形等信息，獲得的戰場信息量少，因此不利于把握整體的戰場態勢。應對完全可辨條件下的算法有基于相對位置矢量的灰色起始算法及其擴展多源算法[8-9]，該類算法假定編隊成員用于起始的點跡在各個時刻的相對位置絕對穩定，因此當編隊做整體機動時該算法不適用；進而，基于群模型的精細起始算法[10]解決了這個問題，其利用群模型[11]描述群內成員的運動學特征及相互作用，彌補了前述算法的不足。但是，對于當前的傳感器分辨水平與信號檢測算法[12-14]的能力，不可辨與完全可辨這2種大環境都是較為極端的條件，部分可辨條件下的編隊則是如今常見的情況，也是當前急需解決的問題。在部分可辨條件下，編隊內成員的檢測概率低，同一目標的回波點跡時斷時續，上述算法及傳統的多目標起始算法[15-17]均不能對該條件下的航跡進行有效起始。

為了解決部分可辨條件下編隊目標的精細起始問題，本文借鑒整體圖像匹配[18]的思路，提出了基于Radon變換和Fourier變換后相位相關特性的精細起始算法，并采用仿真數據對該算法的效能進行了驗證。

1 問題描述

設傳感器在k時刻獲得量測集為

Z(k)={zi(k)}i=1,2,…,mk

(1)

式中：zi(k)=[xiyik]為雷達系統輸出量測；mk為回波量測個數。Z(k)中的量測可能來源為編隊目標、多個單目標以及雜波。本文關注的重點是編隊目標的起始，因此單目標與雜波點在編隊分割過程中均被剔除。

本文算法針對的環境條件與完全可辨條件下編隊起始的主要區別與難點在于：Z(k)中編隊目標的檢測概率較低，目標回波的漏觀測情況較為普遍。對k與k+1相鄰時刻的2個預互聯編隊進行精細關聯時，由于某些目標量測的缺失，編隊量測在位置與數量上均不確定是一一對應的關系，若再存在雜波干擾，編隊精細起始的難度相當大。

2 基于相位相關的編隊精細起始算法

完整的編隊起始流程主要包括群分割、群的預互聯以及編隊內成員精細互聯3個部分。因此，這里分別采用了基于坐標映射距離差分的快速群分割、基于編隊中心點的預互聯[8]以及基于Radon變換和Fourier變換后相位相關特性的編隊成員精細互聯算法。具體流程如圖1所示。

圖1 起始算法流程框架
Fig.1 Frame of initiation algorithm

在群分割環節中，目前具有幾種經典的分割算法，且各算法的處理效果相近。考慮到本文算法的整體處理復雜度較高，為了能提高整體處理效率，采用基于坐標映射距離差分的快速群分割算法，可在一定程度上降低算法復雜度；在編隊預互聯環節，采用經典的基于中心點的預互聯算法，處理效果穩定，為后續的精細關聯提供數據基礎；在精細互聯環節，本文提出的基于相位相關的編隊成員精細互聯算法，是借鑒圖像匹配思想，將回波量測看作圖像元素，對圖像進行整體對準，該算法可有效克服由于量測缺失帶來的相鄰時刻量測不嚴格對應的問題，是本文算法的核心環節。

綜上所述，本文針對低可觀測條件下部分可辨編隊精細起始過程中的難點，有針對性地選取對應算法，并在核心的精細互聯環節創造性地采用圖像匹配的思路，解決了漏觀測所帶來的難題。

2.1 基于坐標映射距離差分的快速群分割

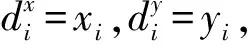
(2)

進而將該序列進行差分運算(后項減前項)，即獲得一個表示相鄰兩點之間距離的序列：

(3)

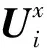
(4)

分群算法的總體流程如圖2所示。由于該算法的時間復雜度較低，比傳統的群分割算法具有效率優勢，因此本文也采用該分群算法提高整體起始效率。

圖2 分群算法流程框架
Fig.2 Frame of group segmentation algorithm

2.2 基于編隊中心點的預互聯

Z(k)完成群分割后形成若干個目標編隊，編隊預互聯的目的是將不同時刻已劃分的編隊進行關聯，確定連續若干時刻內哪些編隊量測來源于同一個編隊，并在相鄰時刻形成一一對應的關系。

(5)

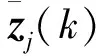
(6)

(7)

(8)

則判定k時刻第j個群與k+1時刻第i個群互聯。式(8)中γ為門限值，其取值根據具體群目標類型而定。

通過將前若干時刻的分群結果進行編隊預互聯，可獲得雷達視場內任意編隊在成員精細互聯過程中所需的所有量測信息。

2.3 基于相位相關特性的編隊成員精細互聯

2.3.1 編隊成員數據空間的描述

在雷達觀測區域內選取某個已完成預互聯的目標編隊Ui，且

Ui={zj(k)}j=1,2,…,mk

(9)

式中：zj(k)為k時刻第j個量測；mk為k時刻編隊量測總數。

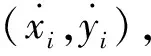
(10)

式中：kend為編隊起始所需要的時刻數。

設置矩形區域的長、寬分別為a、b，且

(11)

對上述矩形區域按N×N平均網格化，則該區域被劃分為N2個面積為(a/N)(b/N)的小矩形網格。定義(xI,yI)(xI=1,2,…,N；yI=1,2,…,N)為網格序號，從而可以按照編隊目標回波落入網格對應的序號，構建編隊數據空間矩陣fk,設置常量C且

(12)

由編隊的定義可知，編隊內各目標的相對位置是緩慢漂移的，編隊的結構在相鄰幾個時刻變化微小，發生仿射變換的幅度較小。因此在航跡起始階段，相鄰時刻的編隊結構只是發生整體的旋轉和平移，從而將該特性作為本文算法的理論基礎。因此，在相鄰時刻fk與fk+1存在以下關系：

fk+1(xI,yI)=fk((xIcosθ0+yIsinθ0)-

CxN/a,(-xIsinθ0+yIcosθ0)-CyN/b)

(13)

式(13)表明，同一編隊的航跡數據空間fk在k時刻經過θ0角度的旋轉，再經過(CxN/a,CyN/b)的平移，即可得到k+1時刻的編隊數據空間fk+1。

2.3.2 編隊結構對準-旋轉角估計

1) 基于Radon變換的旋轉角估計

二維數據空間f(x,y)的Radon變換是該數據空間沿包含該函數的平面內的一組直線的線積分，定義為

R(ρ,θ)=Radon{f(x,y)}=

(14)

根據Radon變換的性質，設相鄰時刻的編隊數據空間fk與fk+1對應的Radon變換分別為Rk(ρ,θ)與Rk+1(ρ,θ)，對式(13)兩邊分別求Radon變換，則存在以下關系：

Rk+1(ρ,θ)=Rk(ρ-ρ0,θ+θ0)

(15)

式中：ρ0=CxNcosθ/a+CyNsinθ/b。式(15)表示fk與fk+1之間存在旋轉角θ0和平移量(CxN/a,CyN/b)的關系。

對于不同的θ，在ρ方向上對式(15)兩邊分別求一維Fourier變換，得到它們在頻域的關系為

(16)

對式(16)兩邊取幅值，即

(17)

(18)

對于所有ω，在θ方向上對式(18)兩邊分別求一維Fourier變換，得到

(19)

(20)

具體而言，旋轉角θ0可通過式(21)求得：

(21)

2) 基于Fourier變換的旋轉角估計

將式(13)兩邊進行Fourier變換，得

Fk+1(u,v)=|Fk(ucosθ0+vsinθ0,

-usinθ0+vcosθ0)|exp(-jφfk+1(u,v))

(22)

式中：Fk(u,v)和Fk+1(u,v)分別為fk(xI,yI)和fk+1(xI,yI)的Fourier變換；φfk+1為fk+1的譜相位，其值主要依賴于平移、旋轉等因素。

對式(22)取模，可以得到其功率譜的關系為

|Fk+1(u,v)|=|Fk(ucosθ0+vsinθ0,

-usinθ0+vcosθ0)|

(23)

從式(23)可以看出，譜中心u=v=0對不同的旋轉角度θ0是不變的。且式(23)是平移不變的，即功率譜會隨著數據空間的旋轉而旋轉相同的角度。

對式(23)進行極坐標變換，令

(24)

則式(23)可推導得到

Sρ(θ,ρ)=Rρ(θ-θ0,ρ)

(25)

因此，已把旋轉量轉化為平移量。對式(25)取Fourier變換，可得

FS ρ(u,v)=FR ρ(u,v)exp[-2jπ(θ0u)]

(26)

式中：FS ρ(u,v)和FR ρ(u,v)分別為Sρ(θ,ρ)和Rρ(θ,ρ)的Fourier變換。則Sρ(θ,ρ)和Rρ(θ,ρ)的互功率譜為

(27)

將式(27)進行Fourier逆變換可得峰值點為(θ0,0)的單位脈沖函數，進而通過尋找峰值點即可得到編隊數據空間相鄰時刻的相對旋轉角度θ0。

2.3.3 編隊結構對準-平移量估計

通過2.3.2節方法獲得旋轉角θ0后，可對數據空間fk進行角度為θ0的旋轉，即

(-xIsinθ0+yIcosθ0))

(28)

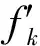
(29)

對式(29)兩邊進行Fourier變換，可得

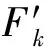
(30)

(31)

(32)

式中：F-1為二維Fourier逆變換。通過式(32)求得CxN/a與CyN/b后，代入已知量N、a和b，即可求得Cx與Cy。

2.3.4 改進的最近鄰精細互聯

通過求取相鄰時刻編隊整體結構的旋轉量與平移量，可將k時刻的編隊航跡點進行整體旋轉與平移補償，從而獲得與k+1時刻相對應的編隊結構(如勻速直線運動的編隊，在無量測誤差、無雜波等完全理想條件下，補償后的航跡點與k+1時刻航跡點重合)。編隊精細起始的最終目的是獲取編隊中各個成員在kend個時刻的起始航跡，因此這里需要對同一成員相鄰時刻的航跡兩兩互聯，從而形成一條完整航跡。但由于部分可辨的觀測條件以及可能存在的雜波等條件，k時刻補償后的點跡與k+1時刻的點跡存在不唯一對應的可能。采用改進的最近鄰法的精細互聯方法，確定kend個時刻內編隊各個成員航跡。

部分可辨條件下，編隊目標發現概率低，即目標的航跡時有時無，航跡信息不完全。根據這個特征，為了最大限度地利用已獲得的航跡信息，在經過編隊結構對準后，點跡關聯的同時采用填補的方式，將有可能缺失的點跡填補上(若填補錯誤，后經判別予以刪除)，從而達到獲取信息利用的最大化。精細互聯的示意圖如圖3 所示。

如圖3所示，編隊中有5個成員，一種標識表示一個時刻的量測，經過將第1時刻航跡與第2時刻航跡補償互聯，目標2與雜波未關聯到航跡，因此在第2時刻增加這2個航跡的虛擬量測(標識為虛線的表示增加的虛擬量測)。再將第2時刻的所有航跡與第3時刻互聯，目標2關聯到了量測，而雜波未關聯到量測。判定目標2為一個目標，并增加第2時刻目標2的量測；同時判定連續2個時刻未關聯到真實量測的航跡為雜波。后續時刻的互聯方式以此類推。

(33)

設閾值為e，則關聯準則為

(34)

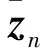
(35)

圖3 精細互聯示意圖
Fig.3 Schematic of refined association

進而在k+1時刻與k+2時刻的精細互聯時，對{zj(k+1)}all進行補償后與{zj(k+2)}利用式(33)、式(34)做關聯判斷。若虛擬量測仍然未關聯到真實量測，則判定其在k時刻為雜波；若虛擬量測關聯到了真實量測，則該虛擬量測判定為該目標在k+1時刻丟失的真實航跡。采用這種先增加虛擬量測，再通過下一時刻的驗證來決定是否留下用于填補航跡，可提高航跡正確起始率，并抑制虛假航跡的產生。

2.3.5 精細互聯算法流程

本節提出的基于相位相關特性的編隊成員精細互聯算法充分考慮了部分可辨編隊的目標回波特點，采用了基于相位相關的整體圖像匹配思想以及增加虛擬量測的最近鄰互聯算法，最大可能地挖掘了編隊成員的航跡信息，可有效對部分可辨編隊成員進行精細起始。該算法流程見圖4。

精細互聯算法的具體步驟如下：

步驟1取編隊預互聯成功的某個編隊，從第1時刻開始，即從k=1開始。

步驟2采用第2.3.2節和第2.3.3節的方法計算{zi(k)}all與{zj(k+1)}之間的旋轉角θ0與平移量(Cx,Cy)。

圖4 精細互聯的算法流程
Fig.4 Flow of refined association algorithm

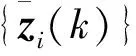
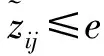
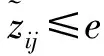
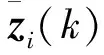
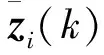
3 仿真驗證與分析

為了驗證本文算法的性能及有效性，本文采用1 000次Monte Carlo仿真對本文提出的基于相位相關的部分可辨編隊精細起始算法與基于相對位置矢量的灰色編隊精細起始算法[8](Group算法)、基于聚類和Hough變換的多編隊航跡起始算法[17](Center算法)和修正的邏輯法[9](Logic算法)在多場景條件下進行航跡起始性能的比較與分析。

3.1 仿真環境

設雷達的采樣周期T=1 s。為了多角度比較分析各算法的航跡起始性能，設置了以下3種經典仿真環境。

1) 環境1 模擬雜波條件下稀疏編隊與密集編隊的目標環境。稀疏編隊目標環境下，編隊成員之間距離一般為(600,1 000) m；密集編隊目標環境下，距離一般為(100,300) m。設在雷達視域內，存在2個編隊與一個單目標做戰術飛行。編隊1為稀疏編隊，做機動飛行，由5個成員組成，初始位置分別為(-5 000,10 000) m、(-5 200,9 400) m、(-4 900,8 600) m、(-5 300,8 000) m、(8 000,9 500) m，初始速度為(-270,270) m/s，初始加速度為(5,-10) m/s2；編隊2為密集編隊，勻速飛行，由4個成員組成，初始位置分別為(5 000,800) m、(5 200,850) m、(5 350,900) m、(5 550,830) m，初始速度為(0,300) m/s。單目標在初始位置(10 000,-800) m上做速度為(-240,200) m/s的勻速直線運動。

仿真中設置雷達視域范圍為：x～[-14 000，10 000] m，y～[-15 000，31 000] m，雷達位于坐標原點(0,0)。在雷達視域范圍內，每個時刻產生1 000個均勻分布的雜波。雷達的測向誤差σθ=0.2°，測距誤差σρ=20 m。設置雷達對目標的發現概率為Pd=0.83，本文算法的kend=6。

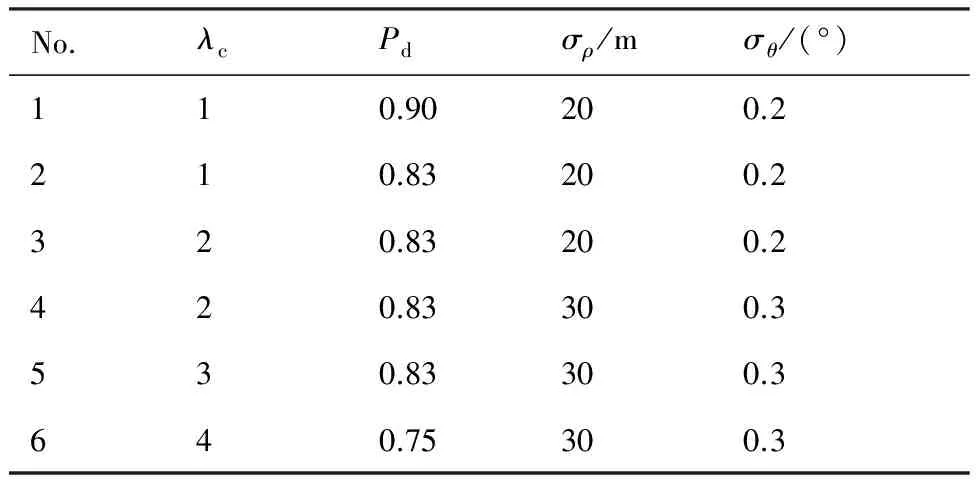
表1 仿真參數取值表(環境2)Table 1 Table of simulation parameters (Environment 2)

3) 環境3 為了研究驗證低可觀測條件對編隊精細起始造成的影響，在該仿真環境中，設置不同的目標發現概率Pd，來驗證本文算法的有效性。設置雷達的測向誤差σθ=0.2°，測距誤差σρ=30 m，λc=4，對環境1中第1個編隊進行航跡起始。Pd取值為0.4～1.0，步長為0.05。

3.2 仿真結果與分析

1) 在仿真環境1中，存在2個編隊與1個單目標，所有目標在雷達視域內的運動態勢如圖5所示。圖6為雜波條件下，雷達視域內前6個時刻的量測分布圖，圖中用圓圈標注的區域分別存在對2個編隊起始所需要的目標量測。圖7為圖6 中標注區域的局部放大圖，圖7中的小圈表示目標回波，點表示雜波。可以看出，由于目標發現概率Pd=0.83，所以編隊目標回波較為雜亂，不易直觀獲得編隊成員的精細航跡信息。

圖5 目標整體態勢(環境1)
Fig.5 Overall situation of targets (Environment 1)

圖6 前6個時刻編隊量測分布(環境1)
Fig.6 Group measurement distribution in the 6 former cycles (Environment 1)

圖7 前6個時刻編隊量測局部放大圖(環境1)
Fig.7 Partially enlarged drawing of group measurement in the 6 former cycles (Environment 1)

圖8為Logic算法、Center算法、Group算法和本文算法對第1個編隊的精細起始比較。從圖8(a)中可直觀看出，Logic算法起始出了多條虛假航跡，已無法辨別真實航跡；圖8(b)中，Center算法僅對編隊中心進行了互聯起始，僅獲得編隊整體態勢，不能獲得每個成員的起始航跡；圖8(c)中，Group算法起始出了4條航跡，但從上至下數第2條航跡并沒有第6時刻的狀態點，也意味著該航跡中斷，因此Group算法僅起始出了3條航跡，且已起始的航跡中存在漏觀測點；圖8(d)中，本文算法起始可準確起始編隊成員的5條航跡，且對其中的漏觀測點進行了航跡填補。

圖9為Logic算法、Center算法、Group算法和本文算法對第2個編隊的精細起始比較。對比圖8與圖9可以看出，在部分可辨條件下，各算法對本文所設置環境的起始效果相近，但由于密集編隊的相對雜波密度低，Group算法在圖9(c)中也起始出了4條航跡，但第4條航跡無第6時刻的狀態點，所以實際成功起始3條航跡。本文算法在對2種條件編隊的起始中均成功起始了所有編隊成員的航跡，且對漏觀測點進行有效填補，對部分可辨編隊的精細起始能力顯著由于其他3種算法。

造成上述結果的原因為：在部分可辨條件下，目標的發現概率低，對某個目標而言，前6個時刻的回波易出現漏觀測，同時存在的環境隨機雜波，顯著增加了航跡起始的難度。Logic算法本身針對的是多目標起始背景，其算法思路為非搶占式2/3邏輯互聯，由于編隊成員運動行為相近，導致出現多條虛假航跡；Center算法思路為基于編隊中心進行起始，因此只能形成一條編隊整體態勢的航跡，不能完成對編隊成員的精細航跡起始；Group算法基于互聯編隊量測的相對位置矢量進行精細起始，該算法對目標發現概率要求較高，在低發現概率時不能有效建立量測的相對位置矢量，雖在成員互聯后的航跡確認中采用3/4邏輯，有一定程度的彌補，但仍難取得理想的效果；本文算法基于各時刻編隊回波的相位相關特性進行整體圖像匹配，又通過最近鄰思路有效建立了成員互聯，采用增加虛假量測驗證的方式最大限度地根據部分回波推斷整體航跡，有效消除了雜波影響，具有較高的航跡正確起始率和較低的航跡錯誤起始率。

圖8 4種算法對第1個編隊航跡起始比較(環境1)
Fig.8 Comparison of track initiation of four algorithms for Group 1 (Environment 1)

圖9 4種算法對第2個編隊航跡起始比較(環境1)
Fig.9 Comparison of track initiation of four algorithms for Group 2 (Environment 1)

2) 通過環境1的仿真可以看出，Center算法無法完成對編隊目標成員的精細起始，因此在環境2的仿真中，只將本文算法與Logic算法、Group算法進行仿真對比。

為對比驗證本文算法對工程應用中主要參數指標的適應能力，對環境2中的6種參數條件進行仿真，給出了3種算法的航跡正確起始率[8](Correct Track Initiation Probability, CTIP)與航跡錯誤起始率(Error Track Initiation Probability, ETIP)隨各指標的變化比較，如表2所示。

衡量指標CTIP與ETIP可表示為

(36)

式中：ΟC為正確起始的航跡個數；ΟE為虛假航跡個數；ΟM為漏起始的航跡個數；Οreal為編隊真實的成員航跡個數。

從表2可以看出，總體上，隨著仿真條件難度的增大，各算法的航跡正確起始率隨之降低，同時航跡錯誤起始率隨之升高。對于CTIP指標，本文算法顯著優于其他2種算法，特別是在序號6的條件下(Pd=0.75)，仍能保持70%以上的起始率，表現優異且穩定。這主要得益于本文算法采用圖像匹配的思想，可最大限度弱化目標發現概率低造成的相鄰時刻編隊結構對準難題，同時在精細互聯階段采用增加虛擬量測后驗的方式，填補航跡空缺，盡可能地保證輸出正確的起始航跡。

表2 3種算法CTIP與ETIP隨參數條件變化比較(環境2)Table 2 Variation of CTIP and ETIP of three algorithms with a variety of parameter conditions (Environment 2)

而Group算法中未對目標部分可辨情況采取對策，因此即使在航跡確認階段采用3/4邏輯，仍未能有效解決復雜的航跡閃爍問題，航跡正確起始率不高。Logic算法因采用非搶占式多目標起始思路，在編隊成員運動狀態相似的情況下，對各時刻量測遍歷所有可能航跡，因此起始的航跡中包含了幾乎所有正確航跡。但由于本文算法可對部分量測缺失條件下的航跡進行填補，因此航跡正確起始率高于Logic算法。對于ETIP指標，本文算法的航跡錯誤起始率顯著低于其他2種算法。Logic算法由于遍歷了所有可能航跡，因此其中包含了大量的虛假航跡，隨著雜波的增大和雷達精度的降低，虛假航跡增長顯著，幾乎不能應用于工程中。Group算法隨著目標發現概率降低和雜波增加，編隊架構已產生較大變換，因此虛假航跡和漏起始航跡均會增大，但其考慮了編隊目標運動相似的特性，因此不會出現錯誤航跡陡增的情況。本文算法通過增加虛擬量測后驗的方式，極大降低了虛假航跡的出現概率，也減少了漏起始航跡的可能，因此本文算法的ETIP指標較低，并相對穩定。

對比序號2與序號3(或序號4與序號5)的仿真條件(目標發現概率與雷達精度相同，僅雜波個數不同)，從本文算法的仿真結果可以看出，雖然雜波個數增加，但CTIP與ETIP指標均變動不大，并保持在一個較高的水平，因此本文算法對雜波具有較好的魯棒性。對比序號1與序號2(僅目標發現概率不同)，各算法的仿真結果均存在較小范圍的變動，而本文算法比其他2種算法穩定，因此本文算法對雷達的目標發現概率條件具有較好的適應性。對比序號3與序號4(僅雷達精度不同)，本文算法較其他2種算法的指標變動最小，說明本文對雷達精度也具有較好的魯棒性。

3) 在仿真環境3中(見圖10)，本文算法的CTIP指標顯著高于其他2種算法，特別在Pd=0.65時，CTIP指標高于Logic算法近30%。從算法原理看，本文算法為應對低觀測概率這一技術難題，采用ICP算法進行整體關聯，又采用虛擬量測后驗方式進行成員航跡的互聯，有效提升了航跡正確起始率，在該場景下效果尤為明顯。

圖10 3種算法的CTIP曲線(環境3)
Fig.10 CTIP curves of three algorithms (Environment 3)

4 結 論

本文針對部分可辨編隊的精細起始問題提出了一種基于相位相關的部分可辨編隊精細起始算法。

1) 本文算法對部分可辨編隊的精細起始效果優異，對比已有算法，具有更高的航跡正確起始率和更低的航跡錯誤起始率，編隊成員精細起始有效性與可靠性顯著。

2) 利用整體圖像匹配思想中相位相關特性，對相鄰時刻的編隊量測進行編隊整體結構對準，有效解決了低目標發現概率情況下的編隊結構對準問題。

3) 在采用最近鄰法做航跡精細互聯時，采用增加虛擬量測后驗的方式，在有效填補航跡缺失、增加正確航跡的同時，降低了虛假量測的產生。

4) 對環境雜波與雷達精度具有較好的魯棒性。

5) 在不同觀測條件下，即不同的目標發現概率條件下，本文算法的航跡正確起始率顯著優于經典算法，對目標發現概率具有很好的適應性。

[1] 黃天俊. 低可觀測目標的檢測跟蹤算法[D]. 西安: 西安電子科技大學, 2012: 1-3.

HUANG T J. The algorithm of detection and tracking for low-observable target[D]. Xi’an: Xidian University, 2012: 1-3 (in Chinese).

[2] 耿文東. 編隊目標跟蹤綜述[C]//第十屆全國雷達學術年會, 北京， 2008: 367-371.

GENG W D. Summarizing of group-target tracking[C]//The 10th China Radar Conference, Beijing, 2008: 367-371 (in Chinese) .

[3] TOU J T, GONZALEZEZ R C. Pattern recognition principles[M]. London: Addison-Wesley Publishing Company, 1974: 124-129.

[4] WANG H L, WANG D S, TIAN L S. A new algorithm for group tracking[C]//2011 CIE International Conference on Radar, Chengdu, 2001: 1159-1163.

[5] 何友, 修建娟, 張晶煒, 等. 雷達數據處理及應用[M]. 第2版. 北京: 電子工業出版社, 2009: 120-122.

HE Y, XIU J J, ZHANG J W, et al. Radar data processing with applications[M]. 2nd ed. Beijing: Publishing House of Electronics Industry, 2009: 120-122 (in Chinese) .

[6] 趙志超, 饒彬, 王雪松, 等. 基于概率網格Hough變換的多雷達航跡起始算法[J]. 航空學報, 2010, 31(11): 2209-2215.

ZHAO Z C, RAO B, WANG X S, et al. Multi-radar track initiation algorithm based on probabilistic Hough transform[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(11): 2209-2215 (in Chinese).

[7] 金術玲, 梁彥, 王增福, 等. 兩級Hough變換航跡起始算法[J]. 電子學報, 2008, 36(3): 590-593.

JIN S L, LIANG Y, WANG Z F, et al. A two-hierarchy hough transform base track initiation algorithm[J]. Acta Electronia Sinica, 2008, 36(3): 590-593 (in Chinese) .

[8] 何友, 王海鵬, 熊偉, 等. 基于相對位置矢量的灰色精細航跡起始算法[J]. 航空學報, 2012, 33(10): 1850-1863.

HE Y, WANG H P, XIONG W, et al. Refined gray track initiation algorithm of group targets based on relative position vectors[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(10): 1850-1863 (in Chinese).

[9] 王海鵬, 熊偉, 何友, 等. 集中式多傳感器群目標灰色精細航跡起始算法[J]. 系統工程與電子技術, 2012, 34(11): 2249-2255.

WANG H P, XIONG W, HE Y, et al. Gray refined track initiation algorithm for centralized multi-sensor group targets[J]. System Engineering and Electronics, 2012, 34(11): 2249-2255 (in Chinese).

[10] GAO F, REN H, WANG J, et al. A novel refined track initiation algorithm for group targets based on group model[J]. Chinese Journal of Electronics, 2014, 23(4): 851-856.

[11] PANG S K, LI J, GODSILL S J. Detection and tracking of coordinated groups[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 472-502.

[12] LI N, CUI G, YANG H, et al. Adaptive detection based on multiple a-priori spectral models for MIMO radar in compound-Gaussian clutter[C]//2015 IEEE International Conference on Radar, Arlington, 2015: 870-875.

[13] XU T, XIN C, XCDONALD M, et al. A multiple-detection probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2015, 63(8): 2007-2019.

[14] LIU R, YI W, KONG L, et al. Particle filtering for target tracking using plot-sequences of multi-frame track before detect[C]//2015 IEEE International Conference on Radar, Arlington, 2015: 495-500.

[15] BELL K L, BAKER C J, SMITH G E, et al. Fully adaptive radar for target tracking. Part II: Target detection and track initiation[C]//2014 IEEE International Conference on Radar, Cincinnati, 2014: 209-314.

[16] CHOI S, CROUSE D, WILLETT P, et al. Multistatic target tracking for passive radar in a DAB/DVB network: Initiation[J]. IEEE Transaction on Aerospace and Electronic Systems, 2015, 51(3): 2460-2469.

[17] 邢鳳勇, 熊偉, 王海鵬. 基于聚類和Hough變換的多編隊航跡起始算法[J]. 海軍航空工程學院學報, 2010, 25(6)： 624-629.

XING F Y, XIONG W, WANG H P. A formation target track initiation algorithm based on clustering and hough transform[J]. Journal of Naval Aeronautical and Astronautical University, 2010, 25(6)： 624-629 (in Chinese).

[18] 宋強. 目標航跡對準關聯與傳感器系統誤差估計技術研究[D]. 煙臺: 海軍航空工程學院, 2010: 28-32.

SONG Q. Target track alignment-correlation and sensor bias estimation technique research[D]. Yantai: Naval Aeronautical and Astronautical University, 2010: 28-32 (in Chinese).

[19] 耿文東. 基于群目標幾何中心的群起始算法研究[J]. 系統工程與電子技術, 2008, 30(2): 269-272.

GENG W D. Study of group-initialization method based on group-target center of geometry[J]. Systems Engineering and Electronics, 2008, 30(2): 269-272 (in Chinese).

Refinedtrackinitiationalgorithmforpartlyresolvablegrouptargetsbasedonphasecorrelation

WANGCong1,2,*,WANGHaipeng1,XIONGWei1,HEYou1

1.InstituteofInformationFusion,NavalAeronauticalandAstronauticalUniversity,Yantai264001,China2.KeyLaboratoryforSpacecraftTT&CandCommunicationundertheMinistryofEducation,Chongqing400044,China

Todealwiththeproblemofrefinedinitiationinpartlyresolvablecondition,arefinedtrackinitiationalgorithmbasedonphasecorrelationisproposedinthispaper.Theradarmeasurementsarepreprocessedbyusingfastgroupsegmentationbasedoncoordinatemappingdistancedifferenceandpre-associationbasedongroupcenterpoint.Tosolvetheproblemofgrouptopologyalignmentinlowtargetdetectionprobabilitycondition,thephasecorrelationcharacteristicsinimagematchingarethenusedincompensationandalignmentoftopologicalstructurebetweenadjacenttimes.Combinedwiththenearestneighbormethod,amethodbyusingvirtualmeasurementandposteriordecisionisproposedtoassociatethegrouptrackrefinedly,whichcanfillthemissingtracks,addmorecorrectones,andatthesametimesuppressthefalseones.Thesimulationresultsshowthatcomparedwiththemodifiedlogicmethodandrefinedgraytrackinitiationalgorithm,thealgorithmproposedhasbetterperformanceincorrecttrackinitiationrateandsuppressionoffalsetrack,beingrobusttoenvironmentclutterandradaraccuracyandmoreadaptabletotargetdiscoveryprobability.

partlyresolvable;trackinitiation;grouptarget;phasecorrelation;imagematching

2016-04-07；Revised2016-05-03；Accepted2016-05-27；Publishedonline2016-07-181514

URL：www.cnki.net/kcms/detail/11.1929.V.20160718.1514.004.html

NationalNaturalScienceFoundationofChina(91538201)

2016-04-07；退修日期2016-05-03；錄用日期2016-05-27； < class="emphasis_bold">網絡出版時間

時間：2016-07-181514

www.cnki.net/kcms/detail/11.1929.V.20160718.1514.004.html

國家自然科學基金 (91538201)

＊

.E-mailcongnavy@hotmail.com

王聰， 王海鵬， 熊偉， 等. 基于相位相關的部分可辨編隊精細起始算法J． 航空學報,2017,38(4):320299.WANGC,WANGHP,XIONGW,etal.RefinedtrackinitiationalgorithmforpartlyresolvablegrouptargetsbasedonphasecorrelationJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):320299.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0163

V243.2； TN953

A

1000-6893(2017)04-320299-12

(責任編輯： 蘇磊， 孫芳)

＊Correspondingauthor.E-mailcongnavy@hotmail.com