空間自旋目標寬帶雷達干涉三維成像方法

孫玉雪， 羅迎， 張群,3， 林永照， 陳春暉

1.空軍工程大學 信息與導航學院， 西安 710077

2.信息感知技術協(xié)同創(chuàng)新中心， 西安 710077

3.西安電子科技大學 雷達信號處理重點實驗室， 西安 710071

空間自旋目標寬帶雷達干涉三維成像方法

孫玉雪1,2,*， 羅迎1,2， 張群1,2,3， 林永照1， 陳春暉1

1.空軍工程大學 信息與導航學院， 西安 710077

2.信息感知技術協(xié)同創(chuàng)新中心， 西安 710077

3.西安電子科技大學 雷達信號處理重點實驗室， 西安 710071

空間目標三維成像可為目標的特征提取、分類與識別提供重要依據(jù)。基于L型三天線干涉成像原理，提出了一種寬帶雷達條件下空間自旋目標干涉三維成像方法。首先，分析了雷達發(fā)射線性調(diào)頻(LFM)信號條件下，空間自旋目標在距離-慢時間平面上的成像特點，建立了基于距離-慢時間平面的空間自旋目標干涉三維成像模型；其次，針對建立的干涉三維成像模型中，不同散射點的回波在距離-慢時間平面上會相互交疊的問題，對回波曲線分離、交叉點處理以及一維距離旁瓣的影響等進行了討論，并給出了解決方法，從而獲得目標三維圖像。與已有方法相比，該方法可有效克服單基雷達三維成像無法獲得目標各散射點真實三維位置以及在雙/多基雷達三維成像時多部雷達回波聯(lián)合處理較困難的問題。最后，仿真實驗結果驗證了所提方法的有效性。

自旋目標； 干涉技術； 雷達成像； 寬帶雷達； 線性調(diào)頻信號； 一維距離像

空間目標探測與識別技術一直以來都是世界各國研究的熱點。由于空間目標大都具有自旋、錐旋、翻滾、進動等多種微動形式，因此基于微動特征提取的空間目標識別技術得到了廣泛研究[1-3]。自旋作為微動形式的一種，通過分析目標自旋引起的回波調(diào)制特征，反演目標上散射點的空間三維分布和三維微動參數(shù)，可為目標的分類與識別提供重要依據(jù)[4-6]。

現(xiàn)有的空間目標三維成像技術，主要有基于單基雷達的三維成像技術和基于雙/多基雷達的三維成像技術[7]。文獻[8]提出在單基雷達下用匹配濾波方法對太空碎片進行三維成像；文獻[9]研究了自旋目標回波在距離-慢時間域的性質(zhì)，提出了基于寬帶復數(shù)后向投影的三維成像算法；文獻[10]提出了基于雙基雷達構型的自旋目標三維圖像定標方法；文獻[11-12]提出了基于T/R-R結構雙基雷達的進動目標參數(shù)估計方法。當采用單基雷達對自旋目標進行三維成像時，由于僅能獲得目標的徑向觀測信息，因此無法確定散射點的真實三維空間位置，且需要利用目標微多普勒信號為正弦調(diào)頻(Sinusoidal Frequency Modulation，SFM)信號這一先驗信息，對于復雜微動目標并不適用。當采用雙/多基雷達對自旋目標進行三維成像時，受限于目標上散射中心的各向異性以及散射點相互之間的遮擋效應，算法復雜，且不利于系統(tǒng)實現(xiàn)。

近年來，針對惰性剛體運動目標的干涉式逆合成孔徑雷達(Interferometric Inverse Synthetic Aperture Radar，InISAR)成像技術已經(jīng)得到了較為深入的研究[13-15]。其基本原理是通過逆合成孔徑雷達(Inverse Synthetic Aperture Radar，ISAR)成像分離目標上不同位置的散射點，再利用干涉處理方法得到散射點的三維分布，獲取目標的實際尺寸。對于空間自旋目標，受限于雷達系統(tǒng)的脈沖重復頻率(Pulse Repetition Frequency，PRF)，在ISAR成像所需小轉(zhuǎn)角內(nèi)的有效回波數(shù)量往往很少，使得傳統(tǒng)的ISAR成像效果不理想，無法有效區(qū)分不同散射點，從而影響對散射點的干涉處理，因此現(xiàn)有InISAR成像方法無法實現(xiàn)對空間自旋目標的有效三維成像。然而，在雷達發(fā)射寬帶信號條件下，自旋引起的調(diào)制特征差異使得各散射點回波在距離-慢時間平面上表現(xiàn)為不同的自旋曲線，據(jù)此可以有效區(qū)分不同散射點的回波，從而提取各散射點回波相位來實現(xiàn)干涉三維成像。因此，本文將InISAR中干涉成像的思路引入到空間自旋目標三維成像技術研究中，基于L型分布三天線結構，提出了自旋目標三維干涉成像方法，在距離-慢時間平面，對不同散射點的自旋曲線進行干涉處理，獲得干涉相位差，并根據(jù)該干涉相位差與散射點坐標之間的關系，對散射點坐標進行重構，實現(xiàn)了不同時刻對散射點的三維成像，有效克服了單基雷達成像無法獲得目標上各散射點真實位置和雙/多基雷達成像中多部雷達回波聯(lián)合處理困難的問題。仿真實驗表明該算法能夠準確獲得散射點的三維分布信息。

1 空間自旋目標干涉三維成像模型

三天線干涉成像系統(tǒng)模型如圖1所示，收發(fā)一體的天線A以及接收天線B、C分別位于雷達坐標系XYZ的(0,0,0)、(L,0,0)和(0,0,L)處，構成兩對相互垂直的基線，基線長度為L。

目標參考點O在雷達坐標系中的坐標為(X,Y,Z)，數(shù)據(jù)錄取初始時刻的坐標為(XO,YO,ZO)。以O點為坐標原點建立兩個坐標系：一是目標坐標系xyz，是為描述目標在三維空間中的轉(zhuǎn)動而建立的，隨目標在三維空間中的運動而運動；二是參考坐標系UVW，坐標軸在任意時刻都分別與雷達坐標系的坐標軸保持平行，隨目標中心的平動而整體平動。它們之間的關系由歐拉角和歐拉旋轉(zhuǎn)矩陣確定[16]。

圖1 三天線干涉成像系統(tǒng)與三維自旋目標幾何關系圖
Fig.1 Geometry of three-antenna interferometric imaging system and 3D rotating targets

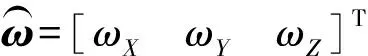
(1)

(2)

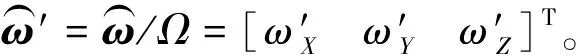
P點到天線A、B、C的距離分別為RAP、RBP和RCP，O點到天線A、B、C的距離分別為RAO、RBO和RCO，M1、M2分別為AB、AC的中點，P到M1、M2的距離分別為RM1、RM2。

假設雷達發(fā)射信號為線性調(diào)頻(Linear Frequency Modulation，LFM)脈沖信號，發(fā)射信號表示為

(3)

采用解線頻調(diào)方法對接收數(shù)據(jù)進行處理，設參考距離為Rref。為了簡化分析，本文采用三天線分別選取各自參考距離的方法進行解線頻調(diào)，即RrefA=RAO,RrefB=RBO,RrefC=RCO，此時可實現(xiàn)各天線所獲得圖像的精確配準。對于天線A有

(4)

(5)

式中：R0為起始時刻P點到A天線的距離；v為目標的平動速度。

將解線頻調(diào)脈壓處理后的差頻回波對快時間(以參考點的時間為基準)進行傅里葉變換，天線A 得到的回波數(shù)據(jù)為

(6)

式中：c為波速；RΔAP(tm)=RAP(tm)-RAO(tm)；σP為P點的散射系數(shù)。將式(6)中后兩個相位項即“剩余視頻相位”項和包絡“斜置”項消除后得到

(7)

同理，天線B和C的回波可分別表示為

SBd(f,tm)=

(8)

SCd(f,tm)=

(9)

當對式(7)取模值可得到散射點的一維距離像

(10)

其峰值位置位于f=-2μRΔAP(tm)/c處，從快時間頻率-慢時間平面(即f-tm平面，由于f通過距離標定可以轉(zhuǎn)化為徑向距離，因此該平面也可稱為距離-慢時間平面)上看，距離像峰值呈現(xiàn)為隨RΔAP(tm)變化的曲線，經(jīng)過平動補償[17-20]處理，RΔAP(tm)中只包含散射點的轉(zhuǎn)動所引起的距離變化，因此該曲線反映了散射點的自旋運動特征。因此，在寬帶雷達中，得益于寬帶雷達的距離高分辨力，可以從距離-慢時間平面來分析目標自旋引起的回波調(diào)制效應。由文獻[16]可知，RΔAP(tm)可表示為

RΔAP(tm)=K+rPcos(Ωtm+θP)

(11)

式中：K為回波曲線在距離-慢時間平面的基線位置；rP為振幅，與散射點的自旋半徑有關；θP為初始相位。因此，根據(jù)不同散射點的自旋半徑、初始相位等信息的不同，可在距離-慢時間平面將不同的散射點進行區(qū)分。并且式(7)中的相位項正是可用于干涉處理的相位信息。因此，本文提出基于空間自旋目標回波的距離-慢時間平面的干涉處理方法，既能有效實現(xiàn)多散射中心回波分離，也能保證準確獲得干涉相位信息以用于三維坐標重構。

對距離-慢時間平面的每個tm時刻回波信號分別進行干涉處理，即可得到干涉相位差為

(12)

(13)

式中：λ為波長。

為保證不發(fā)生相位模糊，應使得|ΔφAB(tm)|<π和|ΔφAC(tm)|<π。由目標和天線的幾何關系可得散射點P在參考坐標系UVW中U軸和W軸隨慢時間變化的坐標分別為

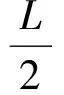
(14)

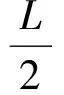
(15)

在遠場條件下，散射點的縱向距離可由一維距離像結合雷達測距信息來獲得，再結合式(14)和式(15)即可獲得目標的三維位置坐標，從而實現(xiàn)對空間自旋目標的三維成像。

2 基于距離-慢時間平面的干涉處理

由第1節(jié)的分析可知，由于自旋目標上各散射點的自旋參數(shù)(如自旋半徑、初相等)存在差異，通過分析微動引起的距離-慢時間平面的回波調(diào)制效應可以分辨不同散射點，并且用于干涉處理的相位信息得以有效保留，因此在寬帶雷達中可以構建一種基于距離-慢時間平面的自旋目標干涉式三維成像方法。在具體成像處理過程中，還需要考慮以下問題。

2.1 散射點回波曲線分離

由式(14)可知，由于不同散射點的RM1、RM2存在差異，利用干涉相位差對不同散射點的坐標進行重構時需要將不同散射點回波進行分離，單獨處理。

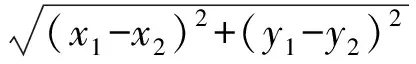
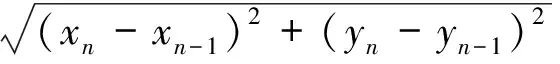
s.t. 1≤xn≤M,1≤yn≤N,yn-yn-1>0,

Sn>ζ,xn∈N,yn∈N

(16)

yn-yn-1>0保證搜索向著同一方向，ζ為設定的閾值，Sn>ζ保證只有幅值超過設定閾值的點才能成為候選點。在曲線交叉處，兩條或多條曲線重疊到同一個點，當用式(16)算法搜索下一個相鄰慢時間時刻的曲線位置時，各條曲線會搜索到同一點，匯集為一條曲線，為避免該問題，利用距離-慢時間平面曲線導數(shù)的連續(xù)性，曲線上相鄰兩點的導數(shù)差很小，且在較短時間內(nèi)曲線的變化趨勢基本不變，進行交叉點處曲線的分離。設曲線在(xn-1,yn-1)點處交叉，利用交叉點之前n0個已經(jīng)分離出的曲線上的點，計算相鄰點之間的導數(shù)并取平均，在每一個曲線交叉點處通過求解如下的最優(yōu)化模型即可搜索分離出該條曲線：

s.t. 1≤xn≤M,1≤yn≤N,yn-yn-1>0,

Sn>ζ,xn∈N,yn∈N

(17)

具體地，從距離-慢時間平面曲線骨架中提取各條曲線的算法步驟為

步驟1初始化：令i=1，d=0，c1×N為零向量。

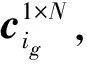
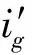
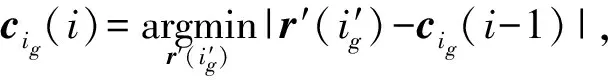
步驟5判斷，當d>D時，終止曲線搜索，轉(zhuǎn)步驟8；當d>D時，令r′=[1 2 …M]，轉(zhuǎn)步驟4。

步驟6令

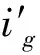
然后轉(zhuǎn)步驟7。

步驟7判斷：當i

步驟8將G個向量cip組成矩陣CG×N，CG×N中的每一行就構成一條提取的曲線。

由此可實現(xiàn)不同散射點回波曲線在距離-慢時間平面的分離。

2.2 距離-慢時間平面“交叉點”的處理

對于距離-慢時間平面上不同余弦曲線相互交叉的部分，由式(7)可以看出，直觀上表現(xiàn)為在慢時間tl時刻散射點具有相同的RΔ(tl)，以兩散射點疊加為例，疊加信號應表示為

(18)

可以看出，由于只有散射系數(shù)σ的疊加，并不影響各自用于干涉的相同的相位信息。但由于距離分辨率的限制，在同一距離分辨單元里，不同散射點之間仍然存在距離差，即散射點RΔ(tl)之間存在差異，式(18)并不成立。該距離差導致回波疊加時相位信息被破壞，使得干涉處理之后得到的散射點坐標位置發(fā)生錯誤，因此對于距離-慢時間平面中的不同曲線交叉部分無法直接對其進行干涉處理，需將其剔除。

由式(10)可知，一維距離像由sinc函數(shù)決定，曲線交叉處是多個sinc函數(shù)的主瓣相互交疊。sinc(a)函數(shù)第一零點在a=1處，對于天線A 距離-慢時間像，即

(19)

式中：-2μRΔ/c為峰值點對應的頻率。因此，第一零點距峰值點頻率差為Δf=1/Tp，所占距離分辨單元數(shù)nx為

(20)

式中：Rresolution為距離分辨率。由于sinc函數(shù)主瓣能量較高，同樣會對干涉相位造成影響，因此對每一交叉點鄰近范圍進行搜索，將同一慢時間時刻，散射點距離-慢時間平面曲線上的點之間的距離向分辨單元數(shù)之差d≤nx的點剔除。具體可在2.1節(jié)曲線分離的基礎上，搜索曲線之間每一慢時間時刻的行序號之差在剔除范圍之內(nèi)的點，并對其進行剔除處理。

2.3 一維距離像旁瓣的影響分析

一維距離像不可避免的存在旁瓣，旁瓣會對其他散射點的干涉相位造成一定影響。為分析旁瓣的影響，假設有兩散射點P和Q，P點和Q點在峰值處的一維距離信號可分別表示為

sP=|AP|ejθ

(21)

sQ=|AQ|ejφ

(22)

式中：AP和AQ分別為點P和Q回波的幅度；θ和φ分別為點P和Q回波的相角。

P點的第m級距離旁瓣可表示為

sPm=ξejθ

(23)

式中：ξ為第m級距離旁瓣的幅值。當其疊加到Q點回波信號峰值上時，所在距離單元信號可表示為

|AQ|ejφ·(1+κχ·ej(θ-φ))

(24)

式中：κ=ξ/|AP|；χ=|AP|/|AQ|。

通過式(24)可見，當疊加了距離旁瓣之后，旁瓣相對幅度κ、兩散射點幅值之比χ以及相位差(θ-φ)項都會對Q點相位產(chǎn)生影響，設疊加距離旁瓣之后Q點的相位為φ′。當旁瓣不存在即κ=0時，相位不發(fā)生改變。

在某一慢時間時刻，假設φ=π/3，(θ-φ)在(-π,π)范圍內(nèi)變化，χ在(0,10]內(nèi)變化時，相位改變量φ′-φ在第1旁瓣κ=-0.217 0、第5旁瓣κ=-0.057 9、第10旁瓣κ=-0.030 3處，隨(θ-φ)、χ的變化情況如圖2所示，可將該變化情況歸納如下：

圖2 干涉相位改變量與幅值比和相位差的關系圖
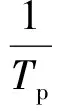
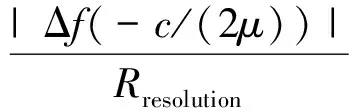
Fig.2 Relationship between interferometric phase change and amplitude ratio and phase difference

1) 相位改變量φ′-φ隨(θ-φ)在(-π,π)的一個周期內(nèi)波動變化，當θ-φ=0時，φ′-φ值達到極小值，此時趨于零。

2) 除θ-φ=-π、0、π處，隨χ的增加，相位改變量逐漸增加。

3) 第1級旁瓣范圍內(nèi)相位改變量最高，旁瓣級越高相位改變量逐漸降低。

4) 在幅值比χ較低的情況下，一般當χ<5時，相位改變量趨于零。

可以看出，由于一維距離旁瓣的影響，當散射點回波之間幅值相差較大時，強回波信號的旁瓣會對弱回波信號的相位造成較大影響；但當幅值相差不大時，旁瓣的影響較小，在一定誤差范圍內(nèi)可以將其忽略。當兩天線進行相位干涉時，兩天線干涉相位改變量的隨機性以及在較短時間內(nèi)疊加旁瓣幅值的波動變化性，使得疊加了距離旁瓣之后的干涉相位差在真實值附近隨機變化。

綜上，對空間自旋目標的三維成像流程圖可歸納如圖3。

圖3 三維成像流程圖
Fig.3 Flow chart of 3D imaging

3 仿真校驗

3.1 兩散射點時

采用圖1所示的三天線結構對遠場自旋運動目標進行仿真分析。初始時刻目標自旋中心位于雷達坐標系的[0 500 0] km處，自旋角速度為ω=[2π 4π 2π]Trad/s，初始歐拉角為[0 π/4 π/5] rad，仿真中假設目標的平動已被精確補償。目標上有兩個散射點，在目標坐標系中的坐標分別為[-2.5 10 5]和[6 -2.5 -15]，單位為m，兩散射點散射系數(shù)均設為1。假設雷達發(fā)射信號載頻為fc=10 GHz，帶寬為300 MHz，照射時間為1 s，脈沖重復頻率PRF=1 000 Hz，距離分辨率為0.5 m，基線長度L=200 m。

三維干涉成像的過程如下：

步驟1對回波信號進行解線頻調(diào)處理，進行一維距離成像，并對距離-慢時間平面不同散射點的回波曲線進行分離，計算sinc函數(shù)第一零點距峰值點之間的距離分辨單元數(shù)為nx=1，將交叉點以及鄰近距離分辨單元數(shù)之差d≤1的點剔除。一維距離像以及骨架提取、曲線分離和交叉點去除結果如圖4(a)～圖4(c)所示。

步驟2對三天線得到的距離-慢時間像進行干涉處理，得到U軸和W軸重構坐標，對于每一交叉點周圍區(qū)域由一維距離旁瓣引起的不理想的重構坐標進行剔除；通過一維距離像得到V維坐標，結果如圖4(g)～圖4(i)所示，真實坐標變化如圖4(d)～圖4(f)所示,其中不同顏色的曲線分別與圖4(c)中對應，代表不同散射點的坐標變化。

圖4 距離-慢時間平面成像以及坐標重構結果
Fig.4 Results of imaging on range-slow time plane and reconstructed coordinate values

步驟3U軸和W軸重構坐標在一維距離旁瓣的影響下，在真實坐標周圍作小范圍的隨機波動，V維坐標受距離分辨率的限制，并不是平滑的曲線。可對三維重構坐標做平滑處理，做曲線擬合的結果如圖4(j)～圖4(l)所示，經(jīng)過曲線擬合之后坐標值的均方誤差(Mean Squared Error, MSE)如表1所示，可見，重構坐標值已經(jīng)極好地逼近真實值。

圖4(m)和圖4(n)給出了在tm=0.15 s和tm=0.8 s兩個時刻的兩散射點三維成像結果，藍色圓圈代表理論成像位置，紅色記號為實際成像結果，從圖中可以看出，三維成像結果與實際相吻合。將成像時間內(nèi)所有慢時間時刻的成像結果獲得的散射點位置進行連接便可得到散射點運動軌跡，如圖4(o)所示。

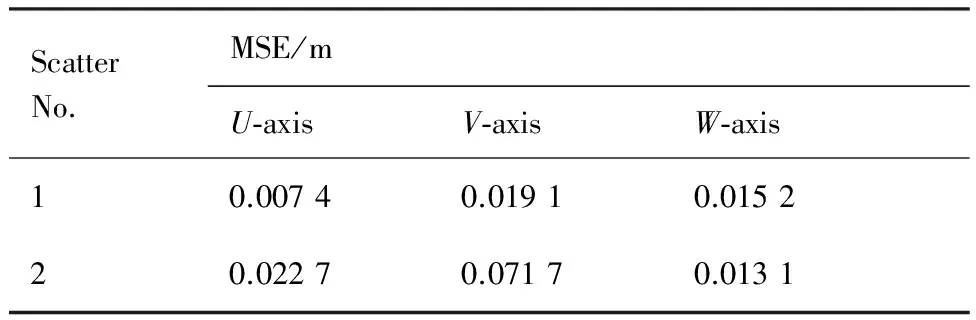
表1 重構坐標值MSETable 1 MSE of reconstructed coordinate values

從仿真結果中可以看出，除了交叉點處以及一維距離旁瓣影響較大的慢時間時刻，采用干涉處理的方法得出的U軸坐標和W軸坐標較好地重構出了真實坐標值，經(jīng)過擬合將坐標曲線進行平滑并將交叉點附近區(qū)域進行連接，更精確地逼近散射點的真實坐標值。

為分析該成像算法在噪聲環(huán)境下的性能，在仿真回波數(shù)據(jù)中加入高斯白噪聲，當信噪比(SNR)為0 dB時，坐標重構結果分別如圖5(a)、圖5(b)和圖5(c)所示。由于高斯白噪聲為隨機分布，對干涉相位以及重構坐標的影響也是隨機的，仍可采用擬合的方法進行平滑。經(jīng)過數(shù)據(jù)擬合之后的坐標如圖5(d)、圖5(e)和圖5(f)所示，重構結果的MSE如表2所示。可以看出，在 0 dB 條件下重構誤差很小，重構結果比較好。但是當信噪比降到-3 dB時，重構誤差已經(jīng)較大，無法得到正確的散射點坐標值。

圖5 信噪比為0 dB時坐標重構結果
Fig.5 Results of reconstructed coordinate values for SNR=0 dB

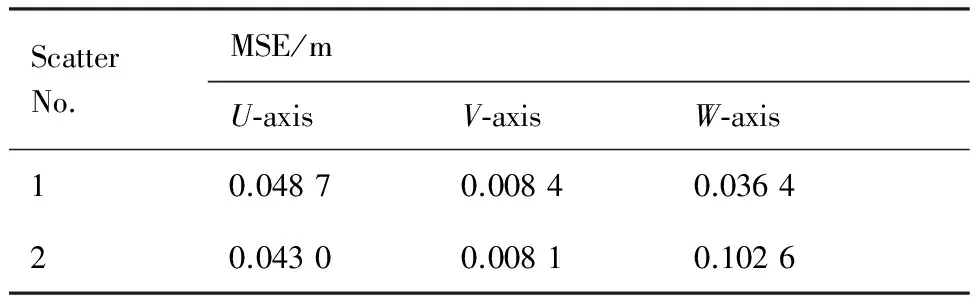
表2 SNR為0 dB時重構坐標值MSE

3.2 多散射點時

在距離-慢時間平面上，不同散射點的一維距離旁瓣會產(chǎn)生相互影響，雖然在2.3節(jié)的分析中已經(jīng)得出當不同散射點的回波幅值相差不大時，一維距離旁瓣的影響很小，在一定誤差范圍內(nèi)可忽略，但當目標上存在多個強散射點，在距離-慢時間平面上，各個散射點產(chǎn)生的回波曲線相互交疊，如果有多個距離旁瓣相互疊加，則可能對干涉相位產(chǎn)生一定影響。為分析多散射點情況下該算法的性能，仿真實驗中，假設目標存在10個散射點，其初始位置分別為[1.5 12 1.5]，[-1.5 -12 -3]，[-2.5 -10 5]，[3.3 8.4 -9.8]，[-2 2.75 -1.2]，[2 20 1]，[-6 -6.5 -10]，[-8 -12 -12.5]，[-2.5 11 5.5],[-8 8 -10]，單位均為m。其他仿真參數(shù)與3.1節(jié)相同。仿真結果如圖6所示。

從重構結果中可以看出，10個散射點的回波曲線在距離-慢時間平面上被分離，圖6(c)中不同曲線代表不同散射點的回波位置。根據(jù)分離出來的十條正弦曲線，采用Hough變換[22]可尋找到各個交叉點所在位置，將交叉點及鄰近一定范圍內(nèi)的點剔除，經(jīng)過干涉處理之后得到U軸和W軸重構結果。從圖6(d)和圖6(e)可以看出，重構結果受到一維距離旁瓣的影響，產(chǎn)生一定的波動，但經(jīng)過曲線擬合之后的坐標仍然能夠很好地逼近真實值。圖6(g)、圖6(h)和圖6(i)對十個散射點坐標曲線的擬合優(yōu)化結果中，每一圖中不同顏色的曲線代表不同的散射點的坐標曲線，三幅圖中同一顏色的曲線分別對應同一散射點的三維坐標曲線。10個散射點的坐標重構誤差如表3所示。U軸重構坐標誤差中MSE值與對應散射點旋轉(zhuǎn)范圍所在圓的直徑的最大比值為3.66%，W軸為3.36%。為驗證多散射點條件下該算法的穩(wěn)健性，在回波中加入5 dB的高斯白噪聲，U軸重構結果如圖7(a)和圖7(b)所示，W軸重構坐標如圖7(c)和圖7(d)所示,圖7(e)為V軸重構坐標。經(jīng)過曲線擬合得到的重構結果的誤差如表3所示，U軸重構坐標誤差中MSE值與對應散射點旋轉(zhuǎn)范圍所在圓的直徑的最大比值為7.24%，W軸為2.34%，可見噪聲與一維距離旁瓣的共同作用既有可能加劇干涉相位的波動，對坐標重構產(chǎn)生不利影響；也可能二者對相位產(chǎn)生的波動相互抵消，從而改善重構精度。

圖6 距離-慢時間平面成像以及坐標重構結果
Fig.6 Results of imaging in range-slow time plane and reconstructed coordinate values

圖7 信噪比為5 dB時坐標重構結果
Fig.7 Results of reconstructed coordinate values for SNR=5 dB

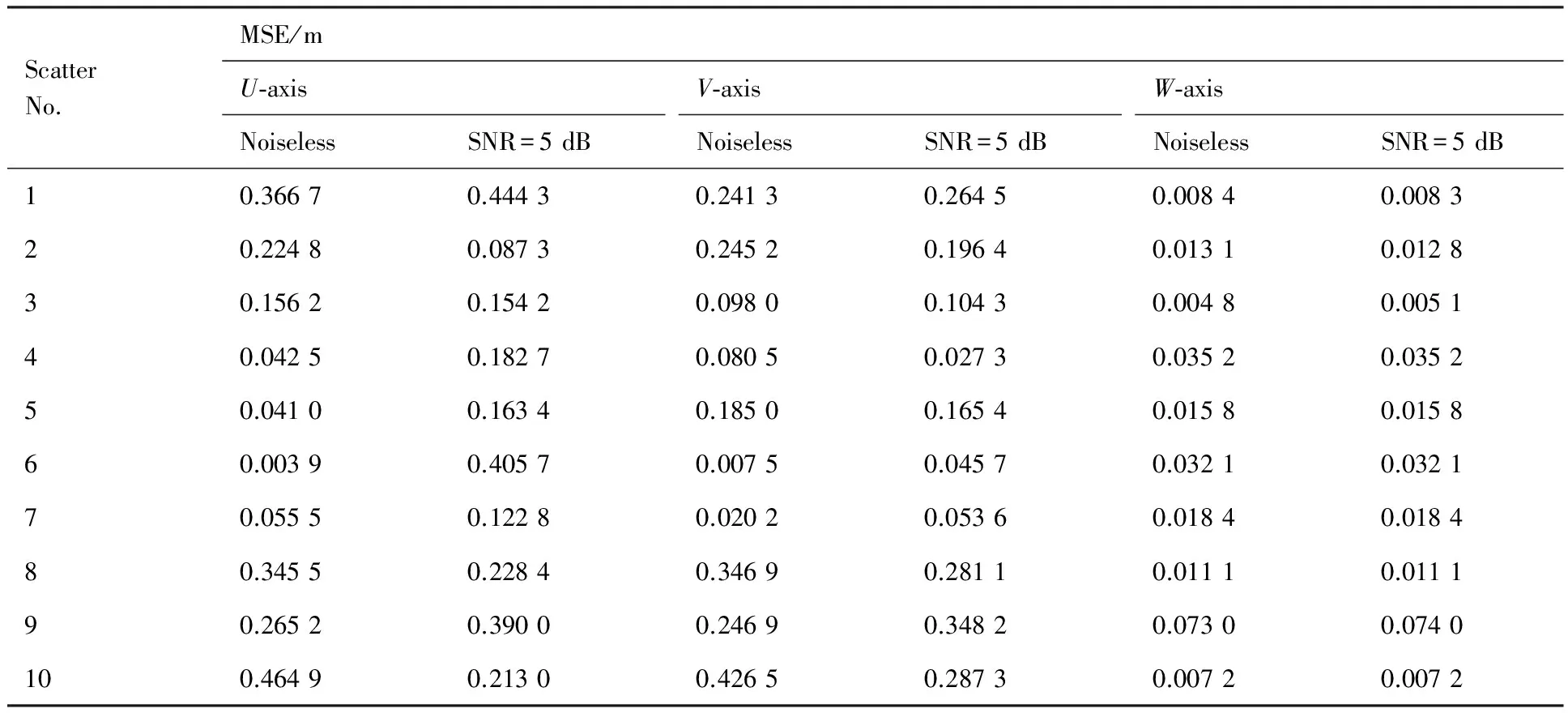
表3 重構坐標值MSETable 3 MSE of reconstructed coordinate values

4 結 論

本文在L型三天線干涉式三維成像體制下，對寬帶信號條件下空間自旋目標三維干涉成像展開了研究。雖然本文是針對自旋目標進行三維成像的研究，但對于其他微動形式如進動，可采取同樣的思路，在距離-慢時間平面進行干涉成像，該方法仍然適用。在低信噪比條件下噪聲對干涉處理的結果影響較大，因此對于強噪聲背景下如何實現(xiàn)準確的三維成像，還需要在以后的工作中進一步予以研究。

[1] SURESH P, THAYAPARAN T, OBULESU T, et al. Extracting micro-doppler radar signatures from rotating targets using fourier-bessel transform and time-frequency analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3204-3210.

[2] LUO Y, ZHANG Q, YUAN N, et al. Three-dimensional precession feature extraction of space targets[J]. IEEE Transactions on Aerospace and Electronic System, 2014, 50(2): 1313-1329.

[3] 肖金國, 杜蘭, 韓勛, 等. 基于參數(shù)化時頻分析的進動錐裙目標瞬時微多普勒頻率提取方法[J]. 電子與信息學報, 2016, 38(1): 90-96.

XIAO J G, DU L, HAN X, et al. Micro-Doppler frequency extraction for cone-skirt shaped target with precession based on parameterized time-frequency analysis[J]. Journal of Electronics and Information Technology, 2016, 38(1): 90-96 (in Chinese).

[4] 畢嚴先, 魏少明, 王俊, 等. 基于最小二乘估計的InISAR空間目標三維成像方法[J]. 電子與信息學報, 2016， 38(5)： 1079-1084.

BI Y X, WEI S M, WANG J, et al. Interferometric ISAR imaging for 3-D geometry of uniformly rotating targets based on least squares estimation method[J]. Journal of Electronics & Information Technology, 2016, 38(5): 1079-1084 (in Chinese).

[5] 尹建鳳, 李道京, 王愛明, 等. 基于星載毫米波順規(guī)-交軌InISAR的空間運動目標三維成像技術研究[J]. 宇航學報, 2013, 34(2): 237-245.

YIN J F, LI D J, WANG A M, et al. Three-dimensional imaging technique of space moving space target based on spaceborne along-cross track millimeter-wave In-ISAR[J]. Journal of Astronautics, 2013, 34(2):237-245 (in Chinese).

[6] 付耀文, 李亞楠, 黎湘. 基于MFT的非勻速轉(zhuǎn)動目標干涉ISAR三維成像方法[J]. 宇航學報, 2012, 33(6): 769-775.

FU Y W, LI Y N, LI X. A 3-D InISAR imaging method for non-uniformly rotating target based on match Fourier transform[J]. Journal of Astronautics, 2012, 33(6): 769-775 (in Chinese).

[7] 陳永安, 羅迎, 王愷, 等. 多天線干涉處理的窄帶雷達空間旋轉(zhuǎn)目標三維成像[J]. 空軍工程大學學報(自然科學版), 2016, 17(4): 46-51.

CHEN Y A, LUO Y, WANG K， et al. Three dimensional imaging for space target based on multi-antenna interferometric processing[J]. Journal of Air Force Engineering University(Natural Science Edition), 2016, 17(4): 46-51 (in Chinese).

[8] XING M, WANG Q, WANG G, et al. A matched-filter-bank-based 3-D imaging algorithm for rapidly spinning targets[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(7): 2106-2113.

[9] BAI X R, XING M D, ZHOU F, et al. High-resolution three-dimensional imaging of spinning space debris[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(4): 2352-2362.

[10] BAI X R, XING M D, ZHOU F, et al. Scaling the 3-D image of spinning space debris via bistatic inverse synthetic aperture radar[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(3): 430-434.

[11] 鄒小海, 艾小鋒, 李永禎, 等. 自旋尾翼彈頭的雙基地微多普勒研究[J]. 電子與信息學報, 2012, 34(9): 2122-2127.

ZOU X H, AI X F, LI Y Z, et al. Bistatic Micro-Doppler of the Spinning Warhead with Fins[J]. Journal of Electronics and Information Technology, 2012, 34(9): 2122-2127 (in Chinese).

[12] AI X F, HUANG Y, ZHAO F, et al. Imaging of spinning targets via narrow-band T/R-R bistatic radars[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(2): 362-366.

[13] CHEN Q Q, XU G, ZHANG L, et al. Three-dimensional interferometric inverse synthetic aperture radar imaging with limited pulses by exploiting joint sparsity[J]. IET Radar Sonar Navigation, 2015, 9(6): 692-701.

[14] MAHDI N, MOHAMMAD H B. A novel model for three-dimensional imaging using interferometric ISAR in any curved target flight path[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3236-3245.

[15] TIAN B, ZOU J W, XU S Y, et al. Squint model interferometric ISAR imaging based on respective reference range selection and squint iteration improvement[J]. IET Radar Sonar Navigation, 2015, 9(9): 1366-1375.

[16] 張群, 羅迎. 雷達目標微多普勒效應[M]. 北京: 國防工業(yè)出版社, 2013: 3-42.

ZHANG Q, LUO Y. Micro-doppler effect of radar targets[M]. Beijing: National Defense Industry Press, 2013: 3-42 (in Chinese).

[17] 羅迎, 柏又青, 張群, 等. 彈道目標平動補償與微多普勒特征提取方法[J]. 電子與信息學報, 2012, 34(3): 602-608.

LUO Y, BAI Y Q, ZHANG Q, et al. Translation motion compensation and micro-Doppler feature extraction of ballistic targets[J]. Journal of Electronics and Information Technology, 2012, 34(3): 602-608 (in Chinese).

[18] 賀思三, 趙會寧, 張永順. 基于延遲共軛相乘的彈道目標平動補償[J]. 雷達學報, 2014, 3(5): 505-510.

HE S S, ZHAO H N, ZHANG Y S. Translational motion compensation for ballistic targets based on delayed conjugated multiplication[J]. Journal of Radars, 2014, 3(5): 505-510 (in Chinese).

[19] 楊有春, 童寧寧, 馮存前, 等. 彈道目標中端平動補償與微多普勒提取[J]. 宇航學報, 2011, 32(10): 2235-2241.

YANG Y C, TONG N N, FENF C Q, et al. Translation compensation and micro-doppler extraction of ballistic targets in midcourse[J]. Journal of Astronautics, 2011, 32(10): 2235-2241 (in Chinese).

[20] 黃大榮, 郭新榮, 張磊, 等. 稀疏孔徑ISAR機動目標成像與相位補償方法[J]. 航空學報, 2014, 35(7): 2019-2030.

HUANG D R, GUO X R, ZHANG L, et al. ISAR phase compensation and imaging of maneuvering target with sparse apertures[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(7): 2019-2030 (in Chinese).

[21] GONZALEZ R C, WOODS R E. Digital image processing[M]. 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 2002: 543-544.

[22] ZHANG Q, YEO T S, TAN H S, et al. Imaging of a moving target with rotating parts based on the Hough transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 291-299.

Interferometric3Dimagingforspacerotatingtargetsinwidebandradar

SUNYuxue1,2，*,LUOYing1,2,ZHANGQun1,2,3,LINYongzhao1,CHENChunhui1

1.InformationandNavigationCollege,AirForceEngineeringUniversity,Xi’an710077,China2.CollaborativeInnovationCenterofInformationSensingandUnderstanding,Xi’an710077,China3.KeyLaboratoryforRadarSignalProcessing,XidianUniversity,Xi’an710071,China

3Dimagingforspacetargetscanprovidegreatsupportforfeatureextraction,andtargetcategorizationandrecognition.BasedonthreeL-shapedantennainterferometricimagingprinciple,aninterferometricmethodfor3Dimagingofspacerotatingtargetsinwidebandradarisproposed.Theimagingfeaturesofspacerotatingtargetsonrange-slow-timeplaneisanalyzedwhenradartransmitslinearfrequencymodulation(LFM)signals.Aninterferometric-processingbased3Dimagingmodelforspacerotatingtargetsisthenestablished.Consideringtheechoesofdifferentscatterswilloverlaponrange-slow-timeplaneinthemodelproposed,somespecificissuessuchasechocurveseparation,overlappedpointdispositionandtheeffectofhighresolutionrangeprofilesidelobeonimagingarediscussed,andthecorrespondingsolutionsareputforward.Generally,themethodhastheadvantageofobtainingthereal3Dpositionoftargetscattersovermonostaticradar-basedimagingmethods,thusavoidingthedifficultyinjointprocessingmultistaticradar-basedimagingmethods.Simulationresultsverifytheeffectivenessoftheproposed3Dimagingmethod.

rotatingtarget;interferencetechnique;radarimaging;widebandradar;chirpsignal;rangeprofile

2016-05-04；Revised2016-10-08；Accepted2016-11-04；Publishedonline2016-11-151013

URL：www.cnki.net/kcms/detail/11.1929.V.20161115.1013.002.html

s：NationalNaturalScienceFoundationofChina(61571475,61471386);ScienceFoundationforPostDoctorateofChina(2015M570815)

2016-05-04；退修日期2016-10-08；錄用日期2016-11-04； < class="emphasis_bold">網(wǎng)絡出版時間

時間：2016-11-151013

www.cnki.net/kcms/detail/11.1929.V.20161115.1013.002.html

國家自然科學基金 (61571475，61471386)； 中國博士后科學基金 (2015M570815)

＊

.E-mailsunyuxuejiayou@163.com

孫玉雪， 羅迎， 張群， 等． 空間自旋目標寬帶雷達干涉三維成像方法J． 航空學報,2017,38(4):320399.SUNYX,LUOY,ZHANGQ,etal.Interferometric3DimagingforspacerotatingtargetsinwidebandradarJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):320399.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0286

V243.2； TN957

A

1000-6893(2017)04-320399-13

(責任編輯： 蘇磊)

＊Correspondingauthor.E-mailsunyuxuejiayou@163.com