γ-Re θt-CF轉(zhuǎn)捩模型在Spalart-Allmaras湍流模型中的推廣及驗證

鞠勝軍， 閻超， 葉志飛

北京航空航天大學 航空科學與工程學院， 北京 100083

γ-Reθt-CF轉(zhuǎn)捩模型在Spalart-Allmaras湍流模型中的推廣及驗證

鞠勝軍， 閻超*， 葉志飛

北京航空航天大學 航空科學與工程學院， 北京 100083

橫流(CF)不穩(wěn)定性是三維流動中誘發(fā)轉(zhuǎn)捩的一項非常重要的因素，考慮到γ-Reθt-CF轉(zhuǎn)捩模型對流向Tollmien-Schlichting波和橫流波不穩(wěn)定性引起轉(zhuǎn)捩的判定均是完全基于當?shù)刈兞浚襍palart-Allmaras(SA)湍流模型計算效率高，因而將γ-Reθt-CF轉(zhuǎn)捩模型與SA湍流模型相結(jié)合，并將其引入開源Standford University Unstructured(SU2)計算流體力學分析平臺。為了考察和驗證模型的預(yù)測精度，分別使用原始γ-Reθt模型和γ-Reθt-CF-SA模型，對NLF(2)-0415后掠翼型和標準6∶1橢球模型進行了轉(zhuǎn)捩預(yù)測數(shù)值模擬。算例結(jié)果表明，γ-Reθt-CF-SA模型的計算結(jié)果與試驗數(shù)據(jù)吻合程度遠遠優(yōu)于原始γ-Reθt模型，γ-Reθt-CF-SA 模型能正確地預(yù)測出三維流動中的橫流不穩(wěn)定性引起轉(zhuǎn)捩的現(xiàn)象。

轉(zhuǎn)捩模型; 橫流不穩(wěn)定性; 基于當?shù)刈兞? 動量厚度; 間歇因子

在航空工程領(lǐng)域，流動不穩(wěn)定性主要是由接觸線不穩(wěn)定性、Taylor-G?rtler渦不穩(wěn)定性、流向Tollmien-Schlichting(T-S)波不穩(wěn)定性和橫流(CF)波不穩(wěn)定性4種擾動波引發(fā)。其中，Taylor-G?rtler渦不穩(wěn)定可以通過消除壁面凹曲來避免。防止接觸線轉(zhuǎn)捩可以通過設(shè)計外形時使接觸線雷諾數(shù)不要超過其臨界值 。因而，T-S波引起的不穩(wěn)定性和橫流不穩(wěn)定性是三維流動中最主要的機制[1]。

在三維流動邊界層轉(zhuǎn)捩預(yù)測方法中，直接數(shù)值模擬方法(DNS)[2]和大渦模擬方法(LES)[3]由于計算量過大很難應(yīng)用到工程計算中；基于線性穩(wěn)定性理論的方法[4-6]在求解過程中需要用到邊界層動量厚度的信息，也難以在現(xiàn)代的CFD并行計算中實現(xiàn)，因而轉(zhuǎn)捩模型方法成為工程領(lǐng)域轉(zhuǎn)捩預(yù)測的主要方法。

在轉(zhuǎn)捩模型的提出與構(gòu)造方面，Coder和Maughmer[7]開發(fā)了基于放大因子的轉(zhuǎn)捩模型、王亮和符松[8]開發(fā)了k-ω-γ轉(zhuǎn)捩模型等。在航空工程領(lǐng)域運用最廣泛的是由Langtry和Menter[9]在2005年提出的γ-Reθt與剪切應(yīng)力輸運(Shear-Stree Transport，SST)湍流模型相結(jié)合的γ-Reθt-SST轉(zhuǎn)捩模型，該模型考慮了自然轉(zhuǎn)捩、Bypass轉(zhuǎn)捩和分離誘導(dǎo)轉(zhuǎn)捩等多種轉(zhuǎn)捩機制，集合轉(zhuǎn)捩經(jīng)驗關(guān)系式和低雷諾數(shù)湍流模型的優(yōu)勢，并首先被耦合到SSTk-ω湍流模型中，由于模型提供了一個將經(jīng)驗公式進行當?shù)鼗幚淼目蚣埽D(zhuǎn)捩的判別都基于當?shù)刈兞?Local Correlation-Based)，因而大大提高了通用CFD用于求解復(fù)雜外形流動的能力，特別是對于三維復(fù)雜情況下的流動。Shivaji和James[10]實現(xiàn)了對γ-Reθt轉(zhuǎn)捩模型與Spalart-Allmaras(SA)湍流模型的結(jié)合，構(gòu)造了具有轉(zhuǎn)捩預(yù)測能力的γ-Reθt-SA模型。但這些模型在構(gòu)造中主要針對流向T-S波不穩(wěn)定性引起的轉(zhuǎn)捩，對于橫流波不穩(wěn)定性引起的轉(zhuǎn)捩預(yù)測精度較差。由此，在轉(zhuǎn)捩模型中考慮橫流的影響得到了深入的研究，比如Jeong[11]、Comelia[12]、Medida[13]、Seyfert[14]、徐家寬[15]等在γ-Reθt轉(zhuǎn)捩模型中，添加了橫流轉(zhuǎn)捩經(jīng)驗判據(jù)。但這些判據(jù)都不是完全基于當?shù)刈兞啃畔ⅲ谇蠼鈺r需要用到邊界層動量厚度的信息，且沒有考慮表面粗糙度對于橫流轉(zhuǎn)捩的影響。針對這些問題，Robin等[16]在2015年提出了完全基于當?shù)刈兞康臋M流不穩(wěn)定性邊界層轉(zhuǎn)捩預(yù)測方法，即γ-Reθt-CF模型，并將其與SSTk-ω湍流模型進行耦合構(gòu)造出γ-Reθt-CF-SST模型，計算結(jié)果令人滿意。γ-Reθt-CF模型沒有推廣耦合到其他湍流模型中，考慮到SA模型計算效率高，被廣泛應(yīng)用于航空工程的數(shù)值計算中，并很容易構(gòu)造雷諾平均Navier-Stokes/LES(RANS/LES)混合方法。本文將γ-Reθt-CF模型與SA模型進行耦合構(gòu)造出γ-Reθt-CF-SA模型，并引入開源Stanford University Unstructured(SU2)計算流體力學分析平臺中。針對三維流動中典型的橫流不穩(wěn)定性引起邊界層轉(zhuǎn)捩問題，選取NLF(2)-0415后掠翼型和標準6∶1橢球模型作為驗證算例，將預(yù)測的轉(zhuǎn)捩起始位置和試驗值進行對比分析，校驗γ-Reθt-CF-SA模型的預(yù)測精度。

1 數(shù)值方法

1.1 γ-Reθt轉(zhuǎn)捩模型

γ-Reθt轉(zhuǎn)捩模型運用基于渦雷諾數(shù)來判斷轉(zhuǎn)捩起始位置，代替動量厚度雷諾數(shù)，實現(xiàn)了完全基于當?shù)刈兞窟M行轉(zhuǎn)捩判據(jù)，因而滿足現(xiàn)在CFD技術(shù)大規(guī)模并行化的計算要求。模型由轉(zhuǎn)捩動量厚度雷諾數(shù)和間歇因子2個輸運方程組成。

1.1.1 轉(zhuǎn)捩動量厚度雷諾數(shù)輸運方程

控制轉(zhuǎn)捩的起始位置是由轉(zhuǎn)捩動量厚度雷諾數(shù)所決定，其值是由轉(zhuǎn)捩動量厚度雷諾數(shù)方程求解得到。轉(zhuǎn)捩起始雷諾數(shù)是一個由來流湍流度和來流壓力梯度組成的非當?shù)鼗暮瘮?shù)。轉(zhuǎn)捩動量厚度雷諾數(shù)輸運方程的生成項由不同的經(jīng)驗公式組成，方程為

(1)

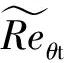
在式(1)中生成項為

(2)

式中：Reθt為轉(zhuǎn)捩動量厚度雷諾數(shù)；Fθt為開關(guān)函數(shù)，(1-Fθt)項用于識別邊界層，在邊界層由內(nèi)到外，由0變化到1。源項系數(shù)Cθt=0.03，擴散項系數(shù)σθt=2.0，tscale用于平衡量綱。

Fθt=

(3)

式中：γ為間歇因子；y為到物面的最小距離；δ為邊界層厚度；系數(shù)ce2=50。由于轉(zhuǎn)捩模型與SA湍流模型耦合，在此模型中Fwake為尾跡區(qū)開關(guān)函數(shù)，取值為1.0。其他項形式為

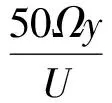
(4)

式中：Ω為渦量的模；U為當?shù)厮俣取＾D(zhuǎn)捩雷諾數(shù)Reθt的值是通過來流湍流度Tu與壓力梯度參數(shù)λθ值擬合的經(jīng)驗公式求解得到，形式為

(5)

式中：壓力梯度參數(shù)為

(6)

式中：θ為邊界層動量厚度；s為流線的弧長。由于Reθt的經(jīng)驗公式的兩端都有未知數(shù)θ值，因而通過迭代法求解，迭代步為10步。

1.1.2 間歇因子輸運方程

間歇因子用于控制邊界層的轉(zhuǎn)捩和邊界層的再層流化，用于決定湍流模型中的渦黏性系數(shù)。間歇因子輸運方程為

(7)

在式(7)中生成項Pγ和耗散項Dγ為

(8)

Dγ=Ca2ρΩFturbγ(ce2γ-1)

(9)

式中：S為平均應(yīng)變率張量的模；擴散項中的系數(shù)為σγ=1.0，源項中系數(shù)的分別為Ca1=2.0，Ca2=0.06，ce1=1.0，ce2=50.0；Flength控制轉(zhuǎn)捩區(qū)長度；Fonset控制轉(zhuǎn)捩的起始位置。轉(zhuǎn)捩的起始位置由式(10)～式(14)確定：

Fonset=max(Fonset 2-Fonset 3,0)

(10)

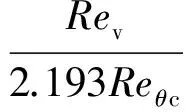
(11)

(12)

(13)

(14)

式中：Rev為流動分離處渦雷諾數(shù)；Reθc為失穩(wěn)動量厚度雷諾數(shù)；RT為湍流黏性比。在與SA模型耦合的中，Shivaji和James[10]通過一系列來流湍流度Tu小于1%，且僅考慮在自然轉(zhuǎn)捩情況下的平板的數(shù)值模擬給出了Reθc及Flength與轉(zhuǎn)捩動量厚度雷諾數(shù)的經(jīng)驗公式，形式為

Reθc=(4.45Tu3-5.7Tu2+1.37Tu+

(15)

Flength=0.171Tu2-0.008 3Tu+0.030 6

(16)

1.1.3 分離誘導(dǎo)轉(zhuǎn)捩

流動發(fā)生分離造成流動失穩(wěn)時，流動分離處渦雷諾數(shù)Rev迅速增長，并接近3.235倍的Reθ c，根據(jù)這個特點Langtry和Menter[9]設(shè)計了分離間歇因子γsep和有效間歇因子γeff，具體表達式為

γsep=

(17)

(18)

γeff=max(γsep,γ)

(19)

式中：Fretattch的作用是當黏性比RT較大時，即當流動再附時，使得分離間歇因子γsep的值趨于0。

1.2 γ-Reθt-CF轉(zhuǎn)捩模型

圖1 橫流流動邊界層內(nèi)速度分布圖
Fig.1 Velocity profiles of crossflow boundary layer

Robin等[16]在2015年提出了基于當?shù)刈兞康膶τ跈M流不穩(wěn)定性引起轉(zhuǎn)捩的判定。在此判定中指定流向的渦量ΩStreamwise值作為邊界層中當?shù)貦M流效應(yīng)的強度指標，并定義渦量ΩStreamwise為

(20)

(21)

(22)

對渦量ΩStreamwise進行無量綱化，定義無量綱化的橫流效應(yīng)的強度為

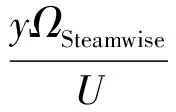
(23)

在轉(zhuǎn)捩動量厚度雷諾數(shù)的輸運方程中，將橫流的影響，以方程中耗散項的形式體現(xiàn)出來，具體公式[16]為

(24)

(25)

(26)

CCrossflow=0.6

(27)

式中：Fθt2項用來限制橫流效應(yīng)的耗散項DSCF的影響范圍，使其只能在層流邊界層內(nèi)起作用；ReSCF項為橫流修正項，是橫流效應(yīng)的主要項，當橫流修正項ReSCF低于轉(zhuǎn)捩的起始位置雷諾數(shù)Reθt時起作用。在二維流動中，ReSCF項為一個較大的數(shù)值，方程退化為原始的γ-Reθt模型。

通過對NLF(2)-0415后掠翼型在不同后掠角下，不同表面粗糙度下的試驗數(shù)據(jù)和線性穩(wěn)定性理論的結(jié)果，建立橫流轉(zhuǎn)捩修正項ReSCF的經(jīng)驗公式。其中，試驗數(shù)據(jù)取自Radeztsky等[17]在1993年完成的NLF(2)-0415后掠翼型的試驗；線性穩(wěn)定性分析則采用eN法。試驗中表面粗糙度h分為3個等級，h取不同的值，高度拋光面(Highly Polished)h=0.25 μm，拋光面(Polished)h=0.5 μm和油漆面(Painted)h=3.3 μm。

對于橫流引起轉(zhuǎn)捩修正項ReSCF的擬合經(jīng)驗公式為

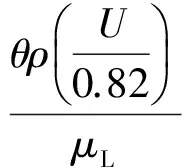
319.51+f(+ΔHCrossflow)-f(-ΔHCrossflow)

(28)

由于ReSCF的經(jīng)驗公式的兩端都有未知數(shù)θt，在本文中采用牛頓法進行迭代求解。式中f(+ΔHCrossflow)和f(-ΔHCrossflow)是關(guān)于ΔHCrossflow的函數(shù)。

ΔHCrossflow是表征著橫流強度的轉(zhuǎn)換項，具體的計算公式為

(29)

f(+ΔHCrossflow)=6 200(+ΔHCrossflow)+

(30)

+ΔHCrossflow=max(0.106 6-ΔHCrossflow,0)

(31)

(32)

-ΔHCrossflow=

max(-1.0(0.106 6-ΔHCrossflow),0)

(33)

轉(zhuǎn)捩動量厚度雷諾數(shù)的輸運方程中的其他項及間歇因子輸運方程與原始γ-Reθt轉(zhuǎn)捩模型相同。

1.3 γ-Reθt-CF轉(zhuǎn)捩模型與SA湍流模型耦合

(34)

(35)

(36)

在方程的求解過程中，γ-Reθt-CF中的2個輸運方程以及SA模型中的湍流輸運方程，均采用有限體積法進行求解，轉(zhuǎn)捩方程和湍流方程均采用松耦合形式與RANS方程結(jié)合，時間推進采用廣義極小殘差(Generalized Minimum RESidual，GMRES)隱式時間格式求解。

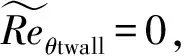
2 算例驗證與結(jié)果分析

為驗證本文所建立的方法的正確性以及考察模型對橫流不穩(wěn)定性引起邊界層轉(zhuǎn)捩的預(yù)測精度，分別選取NLF(2)-0415后掠翼型和標準6∶1橢球模型作為算例，并將數(shù)值模擬的結(jié)果與試驗值進行比較。

2.1 NLF(2)-0415后掠翼型

該模型試驗在亞利桑那州立大學(Arizona State University)的一個低速、低湍流度的風洞中完成。試驗?zāi)Ｐ秃舐咏菫?5°，與來流呈-4° 迎角。試驗狀態(tài)：雷諾數(shù)為Re=1.9×106～6.5×106；來流湍流度Tu=0.09%。試驗中采用萘升華方法測定模型上表面轉(zhuǎn)捩位置。

計算網(wǎng)格如圖2所示，u∞為來流速度，翼型弦長c=1.0 m，為保證物面網(wǎng)格y+<1，第1層網(wǎng)格高度為2×10-6m，法向網(wǎng)格增長率為1.1，網(wǎng)格量為300萬，遠場大約為弦長的20倍，展長為弦長的2.5倍。

選取的計算狀態(tài)為：馬赫數(shù)Ma=0.2，雷諾數(shù)Re=1.92×106～3.73×106，迎角為固定值α=-4°，遠場來流Tu=0.2%，μT/μL=10。

圖2 NLF(2)-0415后掠翼型計算網(wǎng)格
Fig.2 Computational grid of NLF(2)-0415 swept airfoil

圖3給出了NLF(2)-0415后掠翼型轉(zhuǎn)捩方程變量的殘差收斂情況，圖中縱坐標為對數(shù)坐標，lg(residual)表示對變量的殘差取對數(shù)。可以看出，當?shù)竭_到20 000步時，轉(zhuǎn)捩方程的變量殘差可以降到10-3～10-4量級之間，此時認為轉(zhuǎn)捩方程計算收斂。

圖4給出了在表面粗糙度h=3.3 μm時，原始γ-Reθt模型與γ-Reθt-CF-SA模型數(shù)值計算得到的轉(zhuǎn)捩點位置隨雷諾數(shù)變化曲線及其與試驗值和文獻中γ-Reθt-CF-SST模型數(shù)值計算[12]的對比情況。從圖中可以看出，原始γ-Reθt模型在各個雷諾數(shù)條件下，預(yù)測的轉(zhuǎn)捩起始的位置變化不大，轉(zhuǎn)捩位置均在弦長的80%左右。在Re≤2.19×106時，原始γ-Reθt預(yù)測值與試驗值吻合較好，但隨著雷諾數(shù)的增大，橫流效應(yīng)增強，原始γ-Reθt只能預(yù)測出由流向T-S波不穩(wěn)定性引起的轉(zhuǎn)捩，無法預(yù)測由橫流引起的轉(zhuǎn)捩，因而與試驗值相差很大。γ-Reθt-CF-SA模型與γ-Reθt-CF-SST模型預(yù)測出的轉(zhuǎn)捩位置，隨著雷諾數(shù)的增大由71%弦長處提前到15%弦長處，均與試驗值吻合較好。

圖3 NLF(2)-0415后掠翼型轉(zhuǎn)捩方程殘差收斂曲線
Fig.3 Residual history of transition equation of NLF(2)-0415 swept airfoil

圖4 轉(zhuǎn)捩點位置隨雷諾數(shù)變化曲線
Fig.4 Reynolds number effect on transition location

圖5和圖6給出了在表面粗糙度h=3.3 μm時，雷諾數(shù)Re=2.37×106條件下，原始γ-Reθt模型和γ-Reθt-CF-SA模型計算所得的后掠翼型上表面摩擦系數(shù)Cf分布與分布云圖，從兩圖中都可以看出，原始γ-Reθt預(yù)測的轉(zhuǎn)捩起始位置明顯比γ-Reθt-CF-SA模型預(yù)測的位置靠前。這是由于在此雷諾數(shù)下，橫流不穩(wěn)定性已經(jīng)成為誘發(fā)轉(zhuǎn)捩的主要因素，而原始模型未考慮橫流效應(yīng)對轉(zhuǎn)捩的影響。

圖5 NLF(2)-0415后掠翼型上表面摩擦系數(shù)分布
Fig.5 Skin friction coefficient distribution on upper surface of NLF(2)-0415 swept airfoil

圖6 NLF(2)-0415后掠翼型上表面摩擦系數(shù)分布云圖
Fig.6 Skin friction contour on upper surface of NLF(2)-0415 swept airfoil

圖7給出了在表面粗糙度分別為：高度拋光面(Highly Polished)h=0.25 μm，拋光面(Polished)h=0.5μm和油漆面(Painted)h=3.3 μm條件下，在不同雷諾數(shù)下采用γ-Reθt-CF-SA模型計算所得的轉(zhuǎn)捩點的位置與試驗值[17-18]的對比。可以看出在各個表面粗糙度條件下，轉(zhuǎn)捩起始位置與試驗值都吻合較好。其中，在相同的雷諾數(shù)下，隨著表面粗糙度的減小，流動越趨于穩(wěn)定，轉(zhuǎn)捩起始位置越靠后；在相同的表面粗糙度條件下，隨著雷諾數(shù)的增大，流動中慣性力增強，黏性力減弱，流動趨于不穩(wěn)定，轉(zhuǎn)捩點位置提前。

圖7 不同表面粗糙度時，轉(zhuǎn)捩點位置隨雷諾數(shù)變化曲線
Fig.7 Reynolds number effect on transition location for different roughness levels

2.2 6∶1標準橢球模型

該模型試驗是在德國宇航研究院(DLR)的低速風洞中完成，試驗包含多個馬赫數(shù)、雷諾數(shù)和迎角[19]。并且Krimmelbein和Krumbein[20]使用在DLR Tau程序中耦合eN方法也對此模型進行了線性穩(wěn)定性的分析。兩者結(jié)果都顯示：該模型在雷諾數(shù)為Re=6.5×106，馬赫數(shù)Ma=0.13，迎角為5° 和10° 時，轉(zhuǎn)捩由流向T-S波和橫流不穩(wěn)定性共同影響，而迎角為15° 時，橫流不穩(wěn)定性，成為轉(zhuǎn)捩的主要因素。

計算網(wǎng)格如圖8所示，其中，橢球體模型長軸L=1.2 m，為保證物面網(wǎng)格y+<1，第1層網(wǎng)格高度為2×10-6m，法向網(wǎng)格增長率為1.1，網(wǎng)格量為350萬，遠場大約為長軸的20倍。

計算狀態(tài)：來流馬赫數(shù)為Ma=0.13，迎角α=15°，雷諾數(shù)為Re=6.5×106，遠場湍流條件Tu=0.1%和μT/μL=10。

圖9給出了6∶1標準橢球模型轉(zhuǎn)捩方程變量的殘差收斂情況，可以看出，當?shù)竭_到11 500 步時，轉(zhuǎn)捩方程的變量殘差可以降到10-4量級左右，此時認為轉(zhuǎn)捩方程計算收斂。

圖10分別給出了采用原始γ-Reθt模型與γ-Reθt-CF-SA模型數(shù)值模擬得到展開后的橢球表面摩擦系數(shù)分布云圖。其中，三角形離散點為試驗[19]所得的轉(zhuǎn)捩位置，圓形離散點為使用線性穩(wěn)定性理論計算[20]所得的轉(zhuǎn)捩位置，方形散點為文獻[20]中使用γ-Reθt-CF-SST模型計算所得的轉(zhuǎn)捩位置。從圖中可以看出，總的來說，γ-Reθt-CF-SA模型與γ-Reθt-CF-SST模型的預(yù)測的轉(zhuǎn)捩位置與試驗值及線性穩(wěn)定性理論分析的結(jié)果比較相近，且遠優(yōu)于原始γ-Reθt模型的計算結(jié)果。但在橢球體的迎風側(cè)θ=0°～50°，沒有很好地預(yù)測出轉(zhuǎn)捩點的位置，需要對模型進行進一步的修正。

圖8 6∶1標準橢球模型計算網(wǎng)格
Fig.8 Computational grid of 6∶1 prolate spheroid standard model

圖9 6∶1標準橢球模型轉(zhuǎn)捩方程殘差收斂曲線
Fig.9 Residual history of transition equation of 6∶1 prolate spheroid standard model

圖11分別給出了橢球體試驗[19]得到的、采用原始γ-Reθt模型與γ-Reθt-CF-SA模型數(shù)值模擬得到表面摩擦系數(shù)分布云圖。其中，方形散點為文獻[20]中使用γ-Reθt-CF-SST模型計算所得的轉(zhuǎn)捩位置。從圖中可以看出，原始γ-Reθt模型預(yù)測的轉(zhuǎn)捩區(qū)的面積遠遠小于γ-Reθt-CF-SA模型與γ-Reθt-CF-SST模型，這是由于原始γ-Reθt模型只能預(yù)測由T-S波不穩(wěn)定性引起的轉(zhuǎn)捩，而γ-Reθt-CF-SA 模型與γ-Reθt-CF-SST模型能預(yù)測出由T-S波不穩(wěn)定性和CF波不穩(wěn)定性共同作用誘導(dǎo)轉(zhuǎn)捩。

圖10 橢球模型展開后表面摩擦系數(shù)云圖
Fig.10 Unwrapped contour plot of skin friction coefficient contour of prolate

圖11 橢球模型表面摩擦系數(shù)云圖(α=150°，Re=6.5×10,Ma=0.13)
Fig.11 Skin friction coefficient contour of prolate (α=150°，Re=6.5×10,Ma=0.13)

3 結(jié) 論

將具有橫流轉(zhuǎn)捩預(yù)測能力的γ-Reθt-CF模型推廣到SA湍流模型中，并通過NLF(2)-0415后掠翼型和標準6∶1橢球模型對其進行了算例驗證，得出以下結(jié)論：

1) SA湍流模型耦合γ-Reθt-CF轉(zhuǎn)捩模型，具備轉(zhuǎn)捩預(yù)測的能力，與試驗值和線性穩(wěn)定性理論的值對比，吻合度很好。

2)γ-Reθt-CF-SA轉(zhuǎn)捩模型考慮了三維橫流因素以及外形表面粗糙度對轉(zhuǎn)捩的影響，在有橫流效應(yīng)的情況下，預(yù)測精度遠遠高于原始γ-Reθt轉(zhuǎn)捩模型。

3) 通過構(gòu)造當?shù)貦M流效應(yīng)的強度指標，γ-Reθt-CF-SA轉(zhuǎn)捩模型對橫流不穩(wěn)定性引起的轉(zhuǎn)捩判據(jù)完全基于當?shù)鼗兞浚蚨鴮?fù)雜幾何外形以及現(xiàn)代CFD的大規(guī)模并行計算，具有很好的適用性，尤其是將模型引入開源SU2計算流體力學分析平臺中，可以為工程外形的轉(zhuǎn)捩預(yù)測提供有效的手段。

4)γ-Reθt-CF-SA轉(zhuǎn)捩模型在橢球體的迎風側(cè)預(yù)測轉(zhuǎn)捩點的位置與試驗值有些差異，這些方面在后續(xù)的工作中，還需要做進一步研究。

[1] 朱自強, 吳宗成, 丁舉春. 層流流動控制技術(shù)及應(yīng)用[J]. 航空學報, 2011, 32(5): 765-784.

ZHU Z Q, WU Z C, DING J C. Laminar flow control tech-nology and application[J]. Acta Aeronoutica et Astronautica Sinica, 2011, 32(5): 765-784 (in Chinese).

[2] LI X L, FU D X, MA Y W. Direct numerical simulation of hypersonic boundary layer transition over a blunt cone with a small angle of attack[J]. Physics of Fluids, 2010, 22(1): 90-105.

[3] ANTONIOS M, LUCA B, PHIPIPP S.DNS and LES of estimation and control of transition in boundary layers subject[J]. International Journal of Heat and Fluid Flow 2008, 29(2): 841-855.

[4] SU C H, ZHOU H. Transition prediction of a hypersonic boundary layer over a cone at small angle of attack-with the improvement of eNmethod[J]. Science in China Series G: Physics, Mechanics & Astronomy, 2009, 52(1): 115-123.

[5] MICHEL R. Etude de la transition sur les profilsd′aile: Report 1/1578A 192[R]. ONERA, 1952.

[6] MARK D， MICHEL B. Viscous-inviscid analysis of transonic and low reynolds number airfoils[J]. AIAA Journal 1986, 25(10)： 1347-1355.

[7] CODER J G, MAUGHMER M D. A CFD-compatible transition model using an amplification factor transport equation[C]//Grapevine Texas 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Reston: AIAA, 2013.

[8] 王亮， 符松． 一種適用于超音速邊界層的湍流轉(zhuǎn)捩模式[J]． 力學學報， 2009, 41(2): 162-168.

WANG L, FU S. A new transition/turbulence model for the flow transition in supersonic boundary layer[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(2): 162-168 (in Chinese).

[9] LANGTRY R B, MENTER F R. Transition modeling for general CFD applications in aeronautics: AIAA-2005-0522[R]. Reston: AIAA, 2005.

[10] SHIVAJI M, JAMES D B. Application of the correlation-basedγ-Reθttransition model to Spalart-Allmaras turbulence model: AIAA-2011-3979[R]. Reston: AIAA， 2011.

[11] JEONG H S, SOO H P. Modeling and prediction of the crossflow transition using transition transport equations: AIAA-2015-3160[R]. Reston: AIAA, 2015.

[12] COMELIA G, ANDREAS K. Extension of theγ-Reθtmodel for prediction of crossflow transition: AIAA-2014-1269[R]. Reston: AIAA, 2014.

[13] MEDIDA S, BAEDER J D.A new crossflow transition onset criterion for RANS turbulence models[C]//Grapevine Texas 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Reston: AIAA, 2013.

[14] SEYFERT C, KRUMBEIN. A correlation-based transition turbulent modeling for three-dimensional aerodynamic configurations: AIAA-2012-0448[R]. Reston: AIAA, 2012.

[15] 徐家寬， 白俊強， 喬磊, 等． 橫流不穩(wěn)定性轉(zhuǎn)捩預(yù)測模型[J]. 航空學報, 2015, 36(6): 1814-1822.

XU J K, BAI J Q, QIAO L, et al. Transition model for predicting crossflow instabilities[J]. Acta Aeronoutica et Astronautica Sinica, 2015, 36(6): 1814-1822 (in Chinese).

[16] ROBIN B, LANGTRY, KAUSTAV S, et al. Extending theγ-Reθtlocal correlation based transition model for crossflow effects: AIAA-2015-2474[R]. Reston: AIAA, 2015.

[17] RADEZTSKY R H, REIBERT M S, SARIC W S, et al. Effect of micron-sized roughness on transition in swept-wing flows: AIAA-1993-0076[R]. Reston: AIAA, 1993.

[18] DAGENHART J R, SARIC W S. Crossflow stability and transition experiments in swept-wing flow: TP 1999-209344[R]. Washington, D.C.: NASA, 1999.

[19] KREPLIN H P, VOLLMERS H, MEIER H U. Wall shear stress measurements on an inclined prolate spheroid in the DFVLR 3 m×3 m low speed wind tunnel: Report IB 22-84 A 33[R]. G?ttingen: DFVLR-AVA, 1985.

[20] KRIMMELBEIN N, KRUMBEIN A. Automatic transition prediction for three-dimensional configurations with focuson industrial application[J]. AIAA Journal of Aircraft, 2011, 48(6): 1878-1887.

Genevalizationandvalidationofγ-Reθt-CFtransitionmodelingincombinationwithSpalart-Allmarasturbulencemodel

JUShengjun,YANChao*,YEZhifei

SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100083,China

Oneofthemajor3Dtransitionmechanismsistransitionduetocrossflow(CF)instability.Theγ-Reθt-CFtransitionmodelisalocalcorrelation-basedapproachforpredictionoftransitioncausedeitherbyTollmien-Schlichtingsteamwiseinstabilityorcrossflowinstability.Inordertoimprovetheefficiency,γ-Reθt-CF-SAmodeliscoupledwiththeone-equationSpalart-Allmaras(SA)turbulencemodel,andisthenimplementedinopen-sourceStandfordUniversityUnstructured(SU2),aplatformforcomputationalfluiddynamicsanalyses.Inordertovalidateandassesspredictionaccuracyofnewmodel,aseriesoftransitionflowsaresimulatedincludingNLF(2)-0415sweptairfoiland61prolatespheroidstandardmodel.Computationresultsusingγ-Reθt-CF-SAmodelareingoodagreementwithavailableexperimentaldata,farsuperiortothoseusingoriginalγ-Reθtmodel.Modelproposedcaneffectivelypredictlocationofcrossflowinstabilitytransition.

transitionmodel;crossflowinstability;localcorrelation-based;momentumthickness;intermittency

2016-04-28；Revised2016-06-02；Accepted2016-06-25；Publishedonline2016-07-181513

URL：www.cnki.net/kcms/detail/11.1929.V.20160718.1513.002.html

.E-mailyanchao@buaa.edu.cn

2016-04-28；退修日期2016-06-02；錄用日期2016-06-25； < class="emphasis_bold">網(wǎng)絡(luò)出版時間

時間：2016-07-181513

www.cnki.net/kcms/detail/11.1929.V.20160718.1513.002.html

＊

.E-mailyanchao@buaa.edu.cn

鞠勝軍， 閻超， 葉志飛．γ-Reθt-CF轉(zhuǎn)捩模型在Spalart-Allmaras湍流模型中的推廣及驗證J． 航空學報,2017,38(4):120383.JUSJ,YANC,YEZF.Generalizationandvalidationofγ-Reθt-CFtransitionmodelingincombinationwithSpalart-AllmarasturbulencemodelJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):120383.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0205

V221.3

A

1000-6893(2017)04-120383-09

(責任編輯： 鮑亞平， 張晗)