二十面體機構構型設計與分析

劉婧芳 曹亞柯 丁華鋒

(1.北京工業大學機械工程與應用電子技術學院，北京 100124; 2.北京工業大學先進制造技術北京市重點實驗室，北京 100124)

二十面體機構構型設計與分析

劉婧芳1,2曹亞柯1,2丁華鋒1,2

(1.北京工業大學機械工程與應用電子技術學院，北京 100124; 2.北京工業大學先進制造技術北京市重點實驗室，北京 100124)

基于具有對稱性和對偶性的正十二面體，設計了一種以三、四、五邊形為耦合節點的二十面體單移動可展機構。首先，在正十二面體的十個面上添加一種頂點，通過增加頂點種類以增加耦合節點種類，從而得到具有三、四、五邊形結構的節點構件。根據構件連接情況設計四類替換構件，將替換構件用轉動副(R副)依次連接，構造耦合機構基礎模型。其次，基于螺旋理論應用分流法計算其自由度。最后，進行主動輸入選取分析及構建耦合機構的三維模型，設置方向相反的驅動條件分別進行仿真運動，應用Matlab得到動平臺和節點構件的位置變化曲線，仿真結果與理論分析結果相統一，表明提出的機構具有伸縮運動特性。

多環耦合機構； 二十面體； 自由度； 運動分析

引言

隨著機構向復雜化、空間化、多環化發展，近年來多環耦合機構日益受到人們的重視。在結構上，與傳統的并聯機構比較而言，多環耦合機構定平臺和動平臺之間的連接不是若干個獨立支鏈，而是將并聯機構與串聯機構進行有效的結合，使其呈網狀耦合結構。在功能上，多環耦合機構作為串聯與并聯機構的綜合機型，具有特定的應用場合，因此在機構學中吸引了很多學者的關注。李曄卓等[1]用轉動副將平行四邊形縮放單元和雙三角錐單元連接，設計了一種可折疊雙三角錐滾動耦合機構。李菊等[2]設計了多噴槍協同式噴涂五軸機器人。此外，耦合機構常常作為核心機構應用于大型工業機械裝備[3-6]中，以適應其重大承載能力及結構復雜性。

由于正多面體結構具有緊湊結構和高度對稱性等優點，可為多面體耦合機構設計提供基礎。HOBERMAN設計的魔術花球內部結構是典型的六面體耦合機構，通過轉動副將三角形構件、四邊形構件巧妙地組合起來，吸引了研究者應用多種方法對其結構原理和運動特性進行分析[7-12]。俄羅斯宇航局的AKIRA等[13]研制的四面體單元構架式耦合天線，應用于“自然號”、“聯盟號”飛船以及“和平號”空間站上。文獻[14-15]設計了幾種結構多面體耦合機構，這些耦合機構通過改變形狀滿足功能需求，并且已經應用于航空航天。由此可見這類機構具有良好的伸展和收縮性能，在運輸過程可以收縮到極限位置，工作時刻又可以伸展到特定位置實現特有功能。

本文提出一種二十面體單移動機構。以正十二面體的高度對稱性和對偶性的空間結構特點為基礎，設計一種同時由三、四、五邊形為耦合節點的二十面體基礎結構。采用分流法[16-17]求出其自由度，并對其運動輸出特性進行理論分析。進行主動輸入選取并構建耦合機構三維仿真模型，設置方向相反的驅動條件，對機構的動平臺和節點構件的運動特性進行仿真以驗證機構的正確性和合理性。

1 二十面體對稱耦合機構模型構建

正十二面體具有結構簡單，對稱性強等優點，且正二十面體和正十二面體互為對偶，二十面體機構和正十二面體機構在性能上有一定的互補。但二十面體機構更復雜，其理論上的設計難度更大但設計的耦合節點種類更多，在裝配上更難。因此選擇正十二面體構件構建二十面體耦合機構。如圖1所示，一個正十二面體由12個正五邊形、20個頂點和30條棱邊組成，滿足多面體歐拉定理[18]。

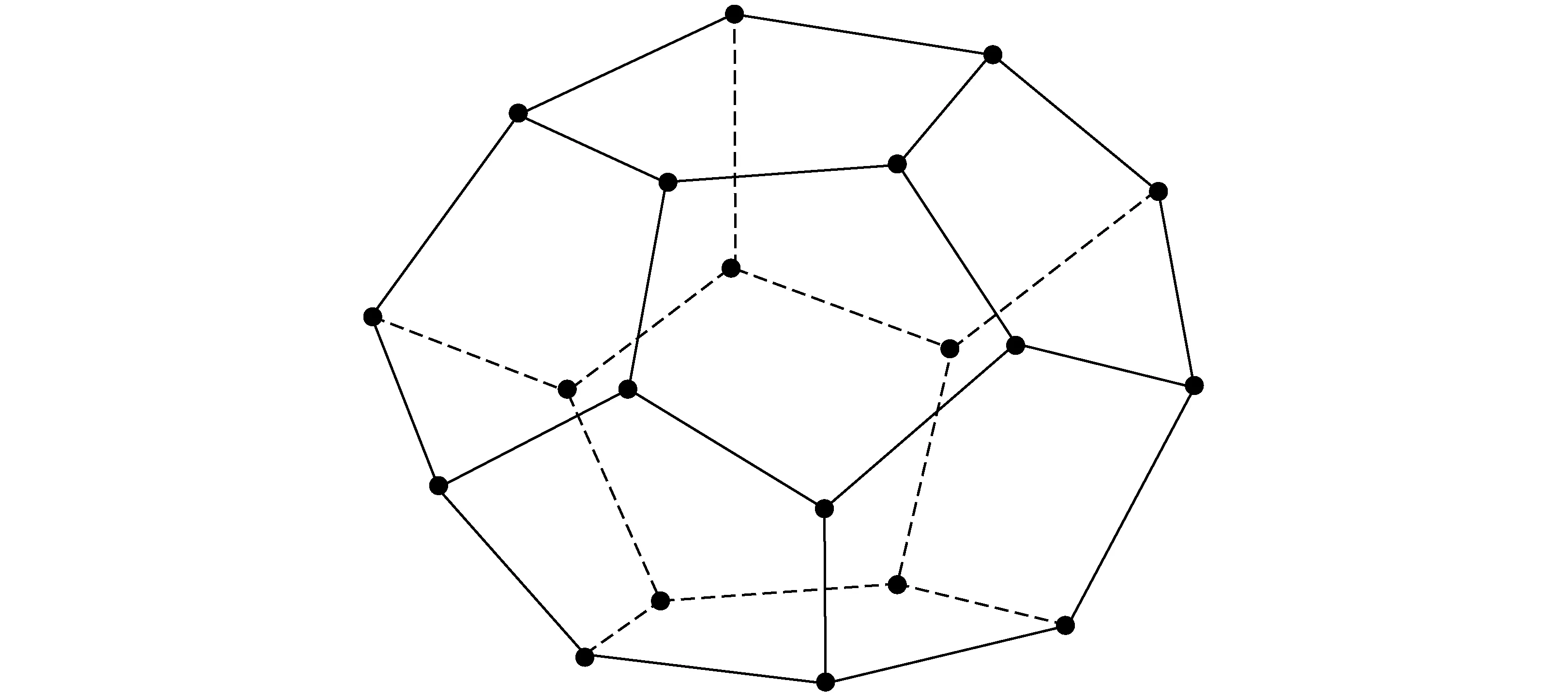
圖1 正十二面體空間結構Fig.1 Structure of regular dodecahedron

1.1 建立耦合框架結構

依照正十二面體空間結構，建立相應的耦合結構基礎框架，再通過確定框架中的頂點和棱邊類型確定各構件類型，從而得到二十面體對稱耦合機構。

(1)標記組成框架的所有幾何要素

考慮到整個耦合結構框架的對稱性和穩定性，將相對平行的2個正五邊形面A1A2A3A4A5和B1B2B3B4B5簡化，分別等效為匯聚了5條棱邊頂點，記為A′和B′，定義為等效頂點。與等效頂點A′直接連接的頂點分別記為C′、D′、E′、F′、G′，與等效頂點B′直接連接的頂點分別記為C、D、E、F、G，與正五邊形面A1A2A3A4A5直接連接的5個面的中心分別記為C′1、D′1、E′1、F′1、G′1，與正五邊形面B1B2B3B4B5直接連接的5個面的中心分別記為C1、D1、E1、F1、G1，如圖2a所示。

圖2 耦合結構框架Fig.2 Frameworks of coupled structure

(2)選擇定平臺和動平臺構件

因為耦合框架結構具有對稱性，選擇互相平行的且匯聚情況相同等效頂點A′和B′為耦合機構模型的定平臺和動平臺構件。

(3)確定耦合節點構件及支鏈組成

為了方便區分頂點種類，如圖2a所示，定義由正五邊形(除正五邊形A1A2A3A4A5和B1B2B3B4B5)棱邊相交的點為一類頂點，用黑色四邊形標示；正五邊形(除了正五邊形A1A2A3A4A5和B1B2B3B4B5)的中心點為二類頂點，用黑色三角形標示。如圖2b所示，將同一個正五邊形上的一個二類頂點分別與3個一類頂點連接，這樣在相鄰正五邊形上的一類頂點之間的公共棱邊替換成以其為對角線的四邊形的4條棱邊，這4條棱邊都是一類頂點和二類頂點之間的連線。一類頂點匯聚了4條棱邊，二類頂點匯聚了3條棱邊，每2個相鄰正五邊形面上的一類頂點和二類頂點的連線交錯相接且呈空間對稱分布，由于每2個相鄰正五邊形因為有一個公共四邊形，使各自所在的運動鏈間存在耦合關系，所以將一類頂點定義為一類耦合頂點，均作為一類耦合節點構件，將二類頂點定義為二類耦合頂點，均作為二類耦合節點構件。如圖2b所示，將能夠確定連接在定平臺A′和動平臺B′之間的由20個耦合節點構件通過連接構件順次連接的各條耦合支鏈。

因此，構建耦合框架結構如圖2b所示，含有20個面、40條棱邊、22個頂點，仍然滿足歐拉公式[18]。

1.2 設計幾何元素的替代構件

基于構建的耦合框架結構中構件的幾何連接關系，采用n邊形構件替代n條棱邊匯聚的頂點的原則，設計4種替代構件。

為了滿足構件之間相對運動的靈活性和簡單性，本文耦合機構模型的運動副的構型設計只考慮R副。設計的4種類型的替代構件分別為：

(1)等效頂點A′和B′處連接了5條對稱且相等的棱邊，將其設計成圖3a所示的正五邊形替代構件。

(2)一類耦合頂點連接了4條棱邊，圖3b所示的四邊形構件代替。

(3)二類耦合頂點連接了3條棱邊，圖3c所示的三角形構件代替。

(4)耦合框架中的每條棱邊用圖3d所示的一個二副桿替代，其兩端R副軸線相互平行。

圖3 替換構件Fig.3 Replaced components

1.3 構建耦合機構模型

依照耦合結構框架的空間布局，所有的替代構件用R副順次連接，構建耦合機構模型。

按照圖2b所示耦合框架結構，選擇2個正五邊形，10個正三角形，10個四邊形，40個連桿替代構件依次連接，得到圖4所示的二十面體耦合機構模型。其中，構件M1和D1分別替代等效頂點A′和B′，構件Li(i=1,2,…,10)分別替代一類頂點，構件Sj(j=1,2,…,10)分別替代二類頂點。然后再將構件Li(i=1,2,…,10)和構件Sj(j=1,2,…,10)，動平臺及定平臺通過40條相同的棱邊連接，從而形成由三、四、五邊形組成的二十面體單移動多環耦合機構(圖4)。

圖4 二十面體耦合機構Fig.4 Icosahedron coupling mechanism

如圖4所示，一個二十面體單移動多環耦合機構包含20個面，40條棱邊，22個頂點，滿足多面體歐拉定理[19]。

2 二十面體機構的解耦及自由度分析

運用以螺旋理論為基礎的獨立運動分流標記法[16-17]對上述構建的耦合機構基礎模型的自由度數目及動平臺的運動性質進行分析，從而驗證構建耦合機構的正確性。

2.1 獨立支鏈的判別

選擇M1為定平臺,D1為動平臺。按照運動分流法，由于動平臺D1上連接5個轉動副R6、R7、R8、R9和R10，因此將該多環耦合機構拆分為5個獨立運動鏈。R6、R7、R8、R9和R10所在的分支分別記為F1、F2、F3、F4和F5，且耦合結構C1、C2、C3、C4和C5連接在定平臺上，5個分支C1-L6-R63-R6、C2-L7-R73-R7、C3-L8-R83-R8、C4-L9-R93-R9和C5-L10-R103-R10作用在動平臺上，這5個節點構件均有2個運動副指向定平臺，且有3個運動副指向離動平臺最近的節點構件，因此相對于定平臺連接的各節點構件又拆分為3個獨立鏈Ck1、Ck2和Ck3(k=1,2,…,5)。如圖4所示，將機構動平臺實現的運動傳輸路線用箭頭在構建的耦合結構中標出。

因為在初始時刻拆分的5個獨立運動鏈關于中心點O分布對稱，故分析自由度時分析其中的1條獨立運動鏈即可，這里分析圖4中第一分支法F1：C1-L6-R63-R6,該分支的結構組成如圖5所示。

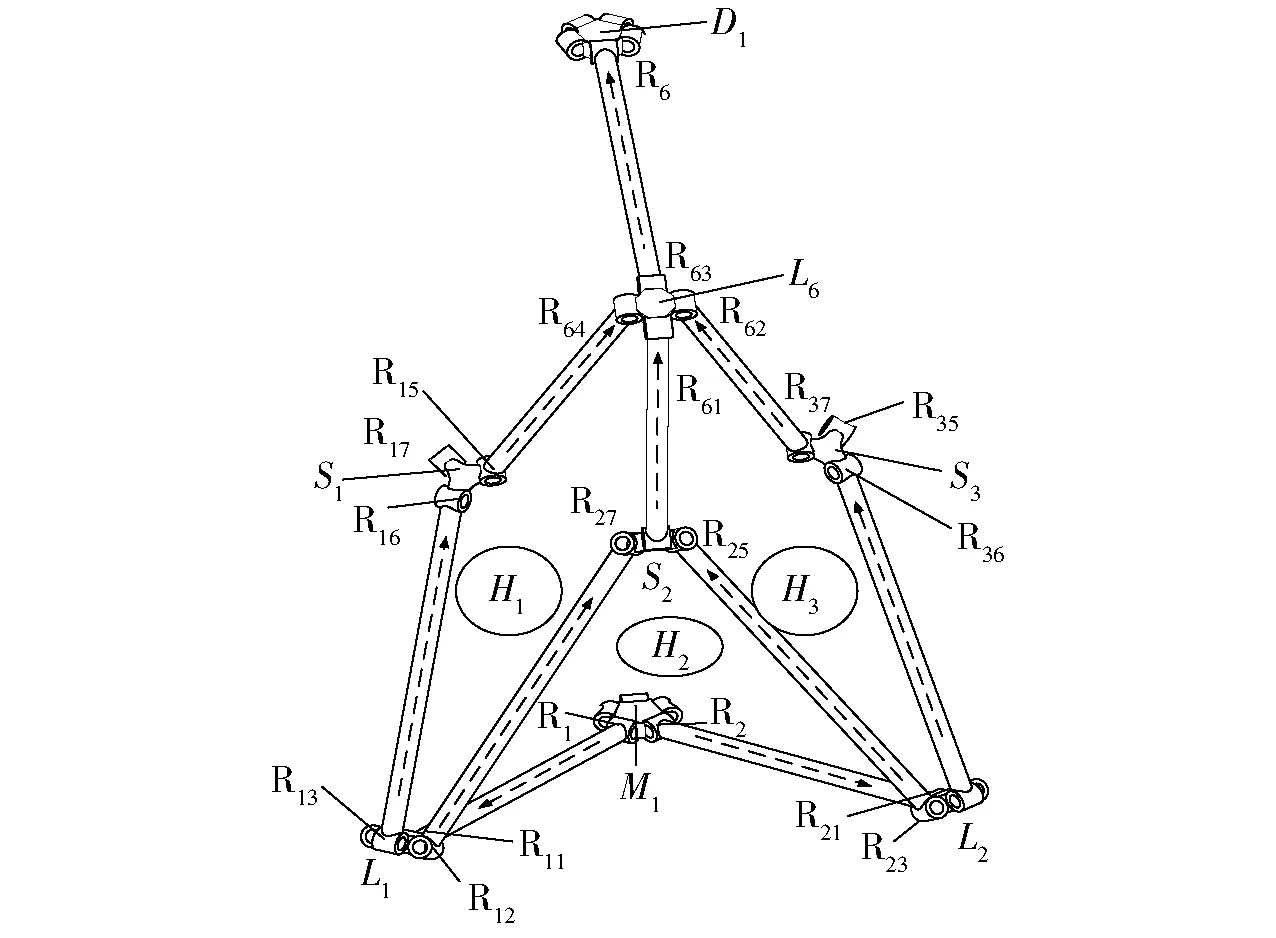
圖5 分支F1Fig.5 Branch F1

2.2獨立運動鏈分支C1的分析

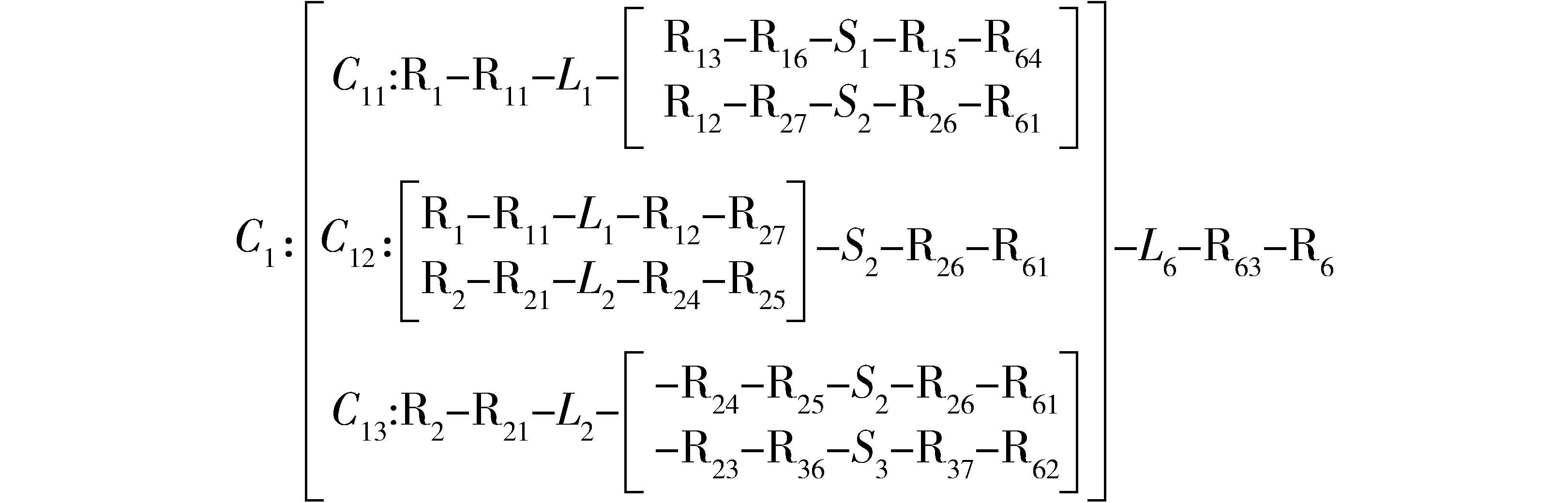
圖6 分支F1結構框圖Fig.6 Block diagram of branch F1

初始時刻，各個獨立運動分支是里面含有一個人字形構件的“六邊形”，所以每個分支本身有各自的對稱平面。耦合結構C1可以等效為圖6所示中的3條并聯支鏈，分別標記為C11、C12和C13。每個并聯支鏈都包含一個八桿單環結構，分別標記為H1、H2、H3(圖5)。

對于分支C12，為了方便建立坐標系，對圖5中分支C1的鏡像視圖進行分析，如圖7所示。

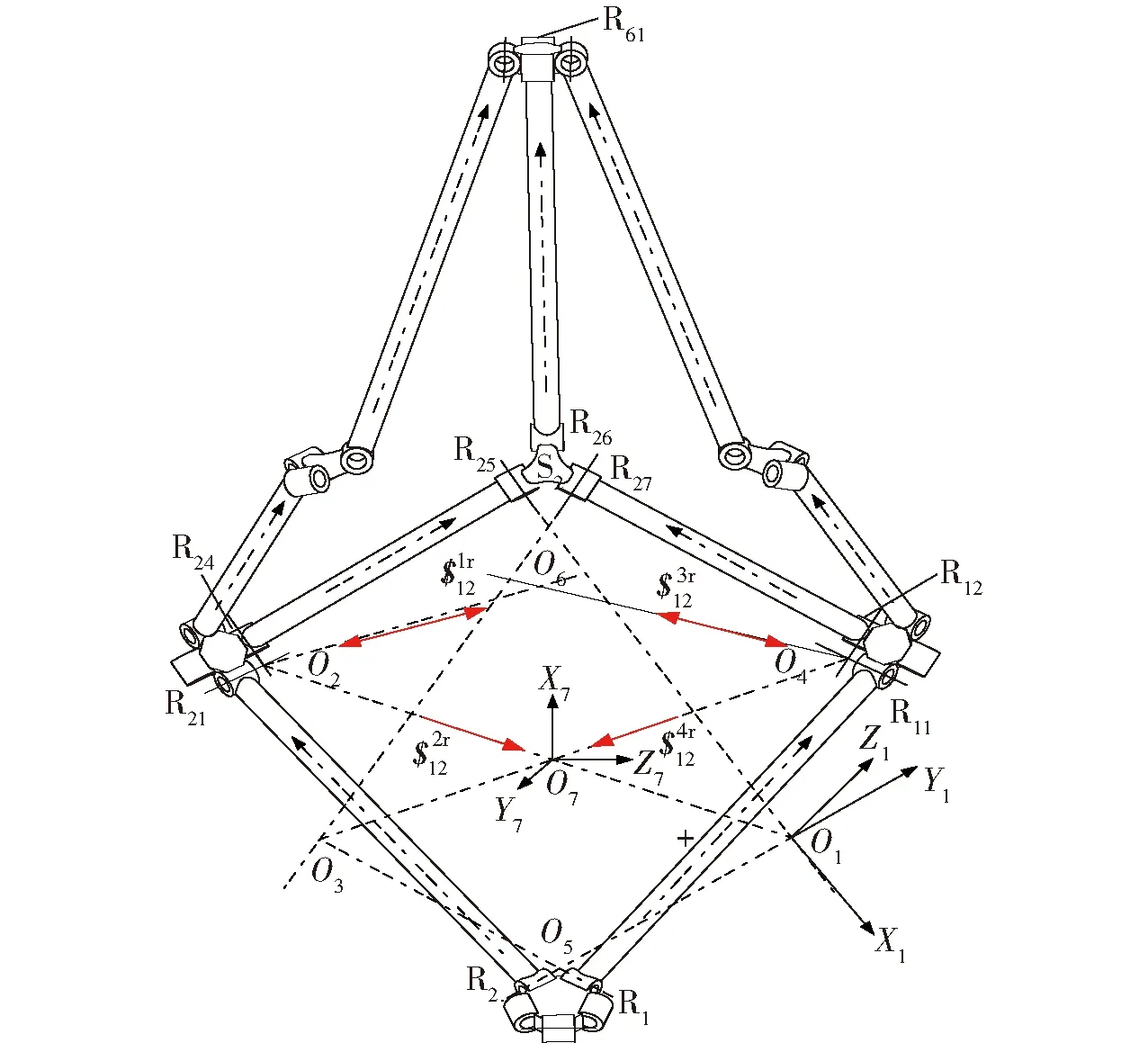
圖7 分支和的約束分析Fig.7 Constraint analysis of branch and

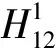
(1)

(2)

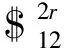
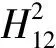
(3)

求反螺旋，得到分支C12的約束螺旋系為

(4)

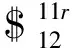
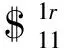
對于耦合節點L6,在坐標系O7X7Y7Z7中約束螺旋系為

(5)

L6的運動螺旋系為

(6)

分支C1-R6的運動螺旋系為

(7)

反螺旋為

(8)

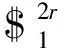
2.3 整個機構的分析

由對稱性可知，C1-R6、C2-R7、C3-R8、C4-R9、C5-R105個獨立支鏈也分別施加給動平臺2個約束力偶，每個支鏈的其中一個約束力偶與定平臺M1所在平面垂直且平行于5個分支對稱平面的交線，另一個約束力偶與定平臺M1所在平面平行且通過5個獨立支鏈對稱平面的交線。在定平臺M1上投影為點O的直線L為5個支鏈的對稱平面在初始時刻的交線。使Z軸與L重合，XOY位于M1所在平面，則建立如圖8所示的OXYZ坐標系，使其為整個耦合機構的坐標系。在該坐標系下，5個分支作用于動平臺的約束螺旋系為

(9)

求二次反螺旋為

(10)

由式(10)可以看出，動平臺D1在初始位置只有Z軸方向的移動自由度，即動平臺D1在圖4所示初始位形下運動為沿Z方向的上下移動。由于式(9)中有線性相關的約束螺旋系，因此新的耦合機構具有0個公共約束，5個冗余約束。為了進一步說明所求自由度的正確性，下文用修正的G-K公式法[7]計算新機構在初始位置該機構的自由度。

2.4 等效并聯機構輸出件的自由度分析

圖9 等效并聯機構結構示意圖Fig.9 Schematic diagram of equivalent parallel mechanism

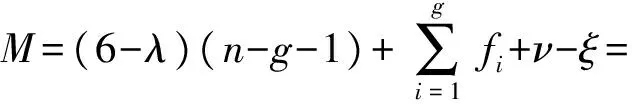
(11)

式中M——機構動平臺D1自由度

λ——公共約束數

n——定平臺構件數目

g——運動副數目

fi——第i個運動副的自由度

ν——并聯冗余約束

ξ——新耦合機構中存在的局部自由度

由于新機構在運動過程中各運動副之間的幾何特性保持不變，因此圖8所示坐標系OXYZ永遠成立，依照2.1～2.3節的拆分原則可得到求解各分支的運動螺旋系也保持不變。那么，新機構依然可以用圖9所示并聯機構等效代替，所以機構的自由度具有全周性，自由度為1。

3 主動輸入選取

機構所選取的輸入數目和機構自由度數應相等，這樣機構才能實現確定的運動。由于本機構只有一個沿Z豎直方向的移動，因此添加一個轉動副，一般選擇機架副。由于本機構具有對稱性，因此在其中一個分支添加驅動即可。因此選擇在R1、R2、R3、R4和R5的任何一個機架副添加驅動作為輸入副即可，本文選擇R2作為主動副。根據趙鐵石等[19]提出的如何判斷添加原動件的方法，對機構的輸入選取進行分析。

基本思想為：將所選作為輸入的所有主動副鎖定后，計算所有分支對于動平臺發生的總的約束反螺旋系

(12)

i——6與機構自由度的差值

即如果剛化后機構總動平臺上的約束反螺旋系的秩$r等于6，即dim($r)=6，則所選擇的輸入是合理的；否則為不合理，重新選擇。

根據上述方法，對于本文提出的二十面體耦合機構，在初始位型下，獨立運動鏈分支C1分支的運動螺旋系為式(1)。在這里剛化轉動副R2，即在分支中去掉轉動副及在式(1)去掉螺旋 。則約束螺旋系式(2)又增加了一個沿X1方向的約束力,且產生對原點的距為沿Y1軸方向的力偶分量可得。

(13)

此時H12變成了7桿機構，原來節點構件S2受過O7點相對于定平臺2個等效廣義運動副，分別為位于對稱平面內的移動和轉動。此時由于轉動副R2剛化，則位于對稱平面內的轉動被約束掉。則在圖7坐標系O7X7Y7Z7中得H12運動螺旋為

(14)

分支H12-R26-R61的運動螺旋系在O7X7Y7Z7中為

(15)

求反螺旋，可得到分支C12的約束螺旋系為

(16)

同理由于環H11、H13都含有與H12中R2沒有剛化前類似的8桿機構，且分支C11、C13關于對稱平面對稱。用相同的分析方法得到對于耦合節點L6，在坐標系O7X7Y7Z7中，其約束螺旋系為

(17)

對其求反螺旋得到L6的運動螺旋為在X7O7Y7面內的移動，從而得到分支C1-R6的運動螺旋系為

(18)

反螺旋為

(19)

在該坐標系下，5個分支作用于動平臺的約束螺旋系為

(20)

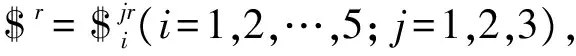
綜上所述，二十面體耦合機構在R2處添加轉動副作為主動輸入是合理的。

4 運動特性分析

應用ProE構建耦合機構的三維實體模型，利用Matlab得到動平臺和節點構件的位置變化曲線，在仿真上來進一步分析二十面體耦合機構的自由度及運動特性。

4.1 耦合機構仿真模型建立

耦合機構的整體坐標系OXYZ如圖8所示，Z軸垂直定平臺M1所在平面豎直向上，X軸與R4軸線平行，Y軸由右手螺旋定則決定，構建耦合機構的三維模型如圖10所示。以動平臺M1、10個四邊形節點構件及10個三角形節點構件的幾何中心為位移測量點。對各構件上位移測量點的位移進行仿真，在給定的驅動條件下，將仿真結果利用Matlab繪制成時間-位移變化曲線。設置2種驅動條件分別進行仿真從而體現耦合機構的伸縮特性。

圖10 驅動1設置Fig.10 Setting of drive 1

4.2 構件運動特性仿真分析(驅動1)

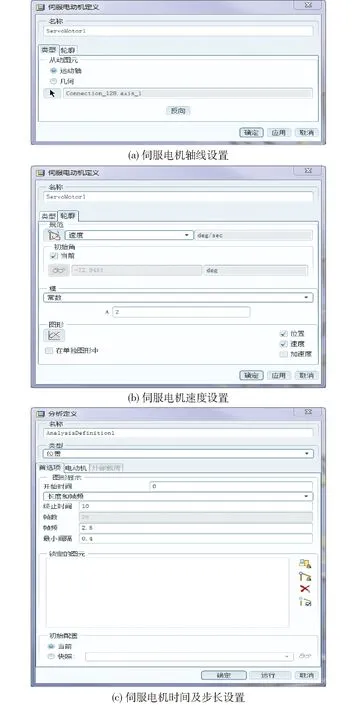
圖11 伺服電機的具體設置Fig.11 Specific settings of servo motor

在R2軸線中點位置設置轉動馬達1，驅動馬達1的旋轉方向用箭頭標注如圖10所示，由右手螺旋法則大拇指沿R2軸線方向指出紙面，馬達1旋轉方向四指握拳方向。馬達選用伺服電機，設置如圖11所示。圖11a表示轉動軸為R1軸線，圖11b表示所加伺服電機的速度為常數2(°)/s，圖11c表示所加伺服電機的終止時間為10 s，幀頻為2.5，最小間隔為0.4 s。

在仿真時間內，動平臺D1沿坐標系OXYZ3個坐標軸的位移變化曲線如圖12所示。由圖12可看出，仿真過程中動平臺沿X軸(下三角符號)和Y軸(實線)的數值始終為0，即D1在這2個坐標軸沒有位移變化，沿Z軸(空心圓)有緩慢的上升趨勢，這表明動平臺只有一個沿Z軸方向的移動運動，符合第2節耦合機構的自由度理論分析結果，說明了設計的機構合理性。

為了分析兩類耦合節點構件的運動特性，將不同的四邊形節點構件Li(i=1,2,…,10)在同一時刻沿各坐標軸的位移變化進行仿真，并繪制相應的時間-位移變化曲線，見圖13；同樣的，三角形節點構件Sj(j=1,2,…,10)在同一時刻沿各坐標軸的位移變化曲線見圖14。

由圖13對比可知，在馬達1驅動條件下，Li(i=1,2,…,5)在Z軸的數值相同，即始終處于同一高度。Li(i=6,7,…,10)在Z軸的數值相同，即始終處于同一高度。其中，耦合構件L4、L6在X軸方向位移始終為0，僅在平面YOZ內運動，沿Y軸數值變化相同但運動方向相反。沿Y軸運動方向相反但數值變化相同，表明平面YOZ為L5和L10的運動對稱平面。構件L1和L9，L2和L8，L3和L7也有與L5和L10相同的位移變化趨勢，所以平面YOZ也是構件L1和L9，L2和L8，L3和L7的運動對稱平面。綜合各坐標軸的仿真結果可知，Li(i=1,2,…,5)和Li(i=6,7,…,10)沿Z軸數值增大的過程中，沿X軸和Y軸的數值均有向0靠近的趨勢，即10個四邊形節點構件在上升過程中，伴隨有向機構對稱中心O匯聚的運動趨勢。

圖14 節點構件Si沿各坐標軸位移變化曲線Fig.14 Changing curves of displacement of joint Si along axes

由圖14可見，在馬達1驅動條件下，Sj(j=1,3,…,9)在Z軸的數值相同，即始終處于同一高度。Sj(j=2,4,…,10)在Z軸的數值相同，即始終處于同一高度。其中構件S2、S7在X軸方向位移始終為0，僅在平面YOZ內運動，沿Y軸數值變化相同但運動方向相反。構件S9、S10在X軸方向位移相同,沿Y軸數值變化相同但運動方向相反，表明平面YOZ為S9和S10的運動對稱平面。構件S1和S8，S3和S6，S4和S5也有與S9和S10相同的位移變化趨勢，所以平面YOZ也是構件S1和S8，S3和S6，S4和S5的運動對稱平面。

綜合各坐標軸的仿真結果，Sj(j=1,2,…,10)沿Z軸數值增大的過程中，沿X軸和Y軸的數值均有向0靠近的趨勢，即10個三角形節點構件在上升過程中，伴隨有向機構對稱中心O匯聚的運動趨勢。

為了體現網狀連接的節點構件Li(i=1,2,…,10)和Sj(j=1,2,…,10)在仿真過程中的位移變化關系，將這20個耦合節點構件與動平臺的運動仿真結果繪制在一個三維空間坐標中，見圖15。

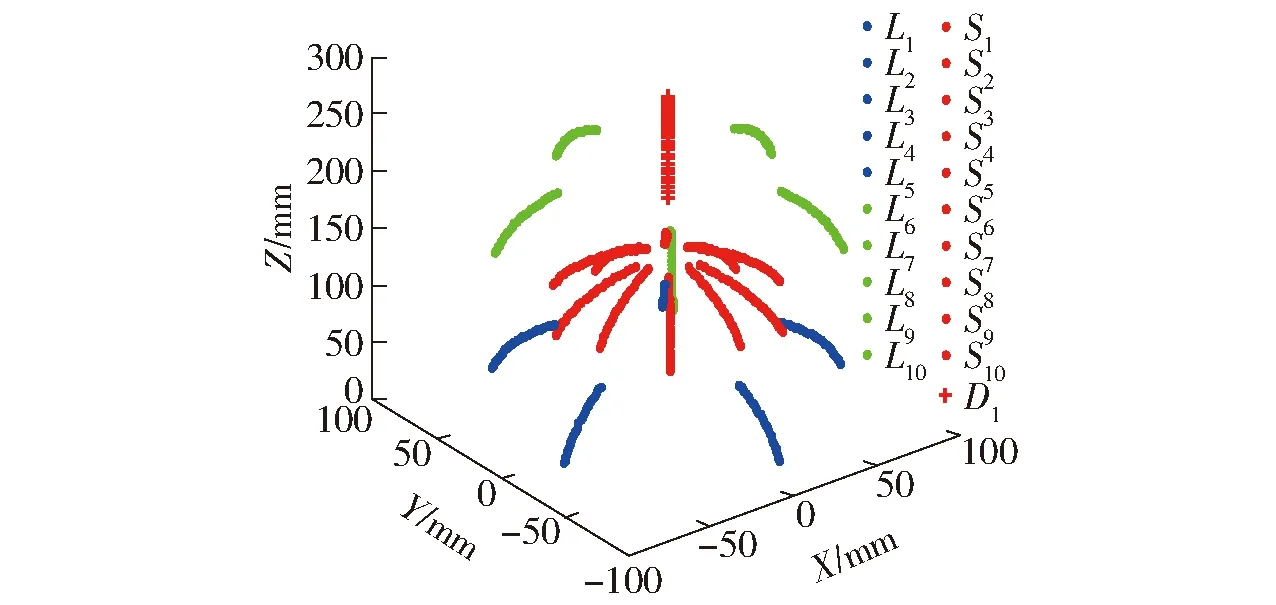
圖15 動平臺及節點構件位移變化曲線圖Fig.15 Changing curves of displacement of moving platform and joints

由圖15可以看出，在馬達1的驅動下，動平臺D1(+號)沿Z軸向上運動過程中，伴隨有耦合節點構件Li(i=1,2,…,10)和Sj(j=1,2,…,10) (圓點)上升并向機構中心O匯聚的運動特性。

4.3 對稱耦合機構可展性

為了對該耦合機構的運動特性進行仿真，設置一個與圖10中馬達1僅轉向相反的驅動條件，以觀察耦合機構運動過程中的收縮運動特性。由仿真結果可以看出，二十面體耦合機構是具有一個移動自由度的對稱可展耦合機構。運動時,耦合點構件Li(i=1,2,…,10)和Sj(j=1,2,…,10)在特定的驅動條件下可以實現往復伸展、收縮運動。圖16是機構在不同仿真時刻對應的位形變化，其中圖16a、圖16b和圖16c為馬達1驅動仿真條件下的位形變形，圖16a、圖16d和圖16e為馬達2驅動仿真條件下的位形變形。

圖16 可展機構位形伸縮變化示意圖Fig.16 Schematic diagrams of deployable mechanism

5 結論

(1)針對正十二面體的對稱性，首先增加頂點種類從而增加耦合節點的種類,設計了一種由三、四、五邊形組成的對稱耦合機構。針對正十二面體的對偶性再構建相應的耦合基礎框架，設計節點替代構件，設計連桿連接耦合節點得到一種二十面體可展耦合機構。

(2)為了判斷整個機構的運動性質，用分流法進行自由度分析，結果表明構建的耦合機構具有1個移動自由度。構建機構的三維實體模型并進行運動特性分析，結果表明了機構的相對耦合節點可實現運動特性相反的運動特性，相鄰耦合節點構件可實現同收縮的運動特性。

1 李曄卓,田耀斌,姚燕安.可折疊雙三角錐滾動機構[J].機械工程學報, 2014, 50(11): 68-79.

LI Yehua, TIAN Yaobin, YAO Yan’an.Foldable triangular bipyramid rolling mechanism[J].Journal of Mechanical Engineering, 2014, 50(11): 68-79.(in Chinese)

2 李菊，趙德安，沈惠平，等.多噴槍協同式噴涂五軸混聯機器人設計[J/OL].農業機械學報, 2012, 43(4): 216-220.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20120441&flag=1.DOI:10.6041/j.issn.1000-1298.2012.04.041.

LI Ju, ZHAO Dean, SHEN Huiping, et al.Design of 5-axes hybrid robot with several spray guns for collaborative spraying[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(4): 216-220.(in Chinese)

3 YAN C, GAO F, GUO W.Coordinated kinematic modelling for motion planning of heavy-duty manipulators in an integrated open-die forging centre[J]．Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2009, 223(10): 1299-1313．

4 丁華鋒,曹宇,楊真真,等.基于D-H法的多連桿正鏟挖掘機運動學分析與包絡圖繪制[J]．燕山大學學報,2014,3(1):197-203．

5 BAKER B.Using an expandable toy in discussing rotational motion[J].Physics Teacher, 2005, 43(4): 247．

6 YOU Zhong.Motion structures extend their reach [J].Materials Today, 2007, 10(12): 52-57.

7 黃真,劉婧芳,李艷文.論機構自由度[M].北京:科學出版社,2011.

8 WEI Guowu, DING Xilun, DAI Jiansheng.Mobility and geometric analysis of the Hoberman switch-pitch ball and its variant [J].Journal of Mechanisms and Robotics, 2010, 2(3): 1049-1059.

9 KIPER G,SOYLEMEZ E,KISISEL A O.Polyhedral linkages synthesized using cardan motion along radial axes[C]∥Proceedings of 12th IFToMM World Congress，Besancon，France, 2007: 471-477.

10 WEI Guowu, DAI Jiansheng.A spatial eight-bar linkage and its association with the deployable platonic mechanisms[J].Journal of Mechanisms and Robotics, 2014,6(2): 021010(1-9).

11 WEI Guowu, YAO Chen, DAI Jiansheng.Synthesis, mobility, and multifuncation of deployable polyhedral mechanisms with radially reciprocating motion[J].Journal of Mechanical Design, Transactions of the ASME, 2014,136(9): 091003(1-12).

12 高慧芳,劉婧芳,余躍慶.向心運動耦合機構設計與分析[J/OL].農業機械學報,2016,47(6):373-380, 356.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160649&flag=1.DOI:10.6041/j.issn.1000-1298.2016.06.049.

GAO Huifang, LIU Jingfang, YU Yueqing.Design and analysis of coupled radial mechanism[J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6): 373-380,356.(in Chinese)

13 AKIRA M, SATESHI H, MITSUNOBU W.Key technologies for high accuracy large mesh antenna reflectors[J].Acta Astronautica, 2003, 53(11): 899-908.

14 ZI Bin, DING Huafeng, CAO Jianbin, et al.Integrated mechanism design and control for completely restrained hybrid-driven based cable parallel manipulators[J].Journal of Intelligent and Robotic Systems: Theory and Applications, 2014, 74: 643-661.

15 楊毅,丁希侖.基于空間多面體向心機構的伸展臂設計研究[J].機械工程學報,2011,47(5):26-34.

YANG Yi, DING Xilun.Design and analysis of mast based on spatial polyhedral linkages mechanism along radial axes[J].Journal of Mechanical Engineering, 2011, 47(5): 26-34.(in Chinese)

16 劉婧芳,黃曉歐,余躍慶，等.多環耦合機構末端件自由度計算的等效法[J].機械工程學報,2014, 50(23): 13-19.

LIU Jingfang, HUANG Xiaoou, YU Yueqing, et al.Equivalent method of output mobility calculation for a novel multi-loop coupled mechanism [J].Journal of Mechanical Engineering, 2014, 50(23): 13-19.(in Chinese)

17 高慧芳,劉婧芳,黃曉歐.基于獨立運動分流標記法的多環耦合機構自由度分析方法[J].北京工業大學學報,2015, 41(11): 1658-1664.

GAO Huifang, LIU Jingfang, HUANG Xiaoou.Method of mobility calculation for a coupled mechanism based on independent motion shunting measurement [J].Journal of Beijing University of Technology, 2015, 41(11): 1658-1664.(in Chinese)

18 薛玉梅.歐拉定理及多面體歐拉公式[J].山西師范大學學報:自然科學版,2009,23(增刊2):6-7,25.

19 趙鐵石,黃真.欠秩空間并聯機器人輸入選取的理論和應用[J].機械工程學報,2000, 36(10): 81-85.

ZHAO Tieshi, HUANG Zhen.The theory and application of input selection for under rank space parallel robot[J].Chinese Journal of Mechanical Engineering,2000, 36(10): 81-85.(in Chinese)

ConfigurationDesignandAnalysisofNovelIcosahedronMechanism

LIU Jingfang1,2CAO Yake1,2DING Huafeng1,2

(1.CollegeofMechanicalEngineeringandAppliedElectronicsTechnology,BeijingUniversityofTechnology,Beijing100124,China2.BeijingKeyLaboratoryofAdvancedManufacturingTechnology,BeijingUniversityofTechnology,Beijing100124,China)

It has remained a great challenge to develop coupled mechanisms in kinematics.Polyhedrons with various appearance and symmetric configuration attract more and more attentions and provide possible basic modes for the design of coupled mechanisms.Based on the symmetry and duality of the regular dodecahedron, a movable icosahedron mechanism with single mobility was designed, where the coupling nodes were composed of triangles, quadrilaterals and pentagons.Firstly, in order to design the coupling nodes with triangles, quadrilaterals and pentagons, each vertex was added to the ten faces of the icosahedron and the node variety was increased by adding types of vertexes.The common edge of the original regular pentagon was replaced by four edges.Four edges made up a quadrilateral.The common edge of the original regular pentagon became a diagonal of the quadrilateral.Then four kinds of replacement components were designed according to the connection of each component, and the replacement components sequentially were connected by rotational joints to construct a basic model of the coupled mechanism.Secondly, mobility of the mechanism model was calculated by the shunting method based on screw theory.The coupled mechanism was divided into five identical branches according to the shunting tags.As long as the constraints of one branch were determined based on screw theory, the constraints of all branches to the moving platform was obtained.Then mobility of the coupled mechanism was obtained, which showed the coupled mechanism had a translational freedom.Finally, active input selection was analyzed and the three-dimensional model of the coupled mechanism was established.Two opposite driving conditions were set up in the simulation, and position curves of the moving platform and the node components were got by Matlab.The simulation results were consistent with theoretical results.It further showed that the proposed mechanism had the characteristics of stretching motion.

coupled mechanism； icosahedron； freedom； motion analysis

10.6041/j.issn.1000-1298.2017.10.048

TH112

A

1000-1298(2017)10-0370-10

2017-05-16

2017-07-31

國家自然科學基金項目(51475015)

劉婧芳(1985—)，女，副教授，博士，主要從事機構學理論和方法設計研究，E-mail: jfliu@bjut.edu.cn