快速LDU三角分解法的研究
席小青,陸節(jié)渙,莊廣宇,陳 懇
(南昌大學信息工程學院,南昌 330031)
快速LDU三角分解法的研究
席小青,陸節(jié)渙,莊廣宇,陳 懇
(南昌大學信息工程學院,南昌 330031)
由于傳統(tǒng)LDU三角分解法中各因子陣元素之間關系不夠清晰,導致計算過程復雜、不易理解,且存貯單元及計算量較大。為此,本文提出快速LDU三角分解法,引入的合成陣既可體現(xiàn)L、D、U元素關系又能大大減少存貯單元;綜合應用“逐行規(guī)格化,按列消元”和四角規(guī)則方式,可無需依賴計算公式直接完成三角分解;在計算過程中改變元素的計算過程,可大大減少計算所需元素的總數(shù)。對各種IEEE節(jié)點系統(tǒng)編程計算,證明了本文所提方法的高效可行。該方法可用于電力系統(tǒng)等各個工程領域?qū)ΤO禂?shù)線性方程組的快速求解。
線性方程;LDU三角分解法;高斯消元;規(guī)格化;四角規(guī)則;電力系統(tǒng)
三角分解法主要用于對常系數(shù)線性方程組的系數(shù)矩陣A進行三角分解,其條件是A陣的前n-1階主子式不等于零。常用的三角分解法有LR、LDU、CU3種,其中LR三角分解法介紹較多[1-14],LDU三角分解法其次[6-15],CU三角分解法較少[10-14],而實際應用較多的是LDU三角分解法(LDU法)。三角分解法在電力系統(tǒng)阻抗矩陣的求解[16-20]、動態(tài)無功優(yōu)化[21]、潮流計算[22-23]等電力系統(tǒng)計算方面應用廣泛,因線性方程組的求解只是其中一小部分。然而,傳統(tǒng)LDU法中L、D、U因子陣的形成雖有多種方式,但由于其計算過程依賴計算公式(公式法),均較為復雜,特別不利于編程計算。且其L、D、U因子陣元素單獨存放需要更多的存貯數(shù)組,各因子陣元素只能用計算公式一次一個地按順序求出,無法利用因子陣元素之間的關系,計算效率不高。
本文為解決上述問題,提出快速LDU法。由于快速LDU法在計算過程不用計算公式(過程法),因此簡單直觀。快速LDU法引入了合成陣的概念,使L、D、U因子陣元素關系一目了然并大大節(jié)省存貯單元;“逐行規(guī)格化,按列消元”使計算過程清晰明了;用四角規(guī)則分步計算L、D、U因子陣元素可大大簡化計算過程并提高計算效率;根據(jù)L、D、U因子陣元素結構的特點進行計算,可減少約40%的元素計算個數(shù)。
1 傳統(tǒng)LDU三角分解法
求解n階線性方程組X,其系數(shù)矩陣為A,線性方程的矩陣形式為

A陣可分解為單位下三角矩陣L、對角陣D和單位上三角矩陣U的乘積,即

展開式(2)可分別得L、D、U3個因子陣,其元素計算公式為
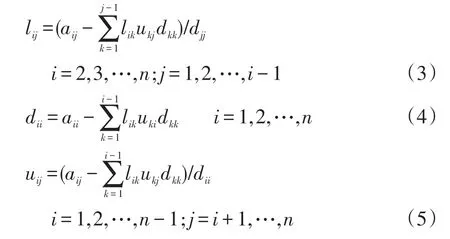
傳統(tǒng)LDU法其形成過程復雜繁瑣、計算量大、不易理解,式(3)~式(5)用于編程計算也比較麻煩。由于傳統(tǒng)LDU法中分別存放A、L、D、U因子陣元素需要4個數(shù)組,計算過程中各元素之間相應的關系無法體現(xiàn)和利用,所有的lij、dii、uij元素完全依賴式(3)~式(5)每次一個計算完成,其計算過程很難簡化或擴展,可將其稱為公式法。
2 快速LDU三角分解法
以四階矩陣為例,將A陣分解為L、D、U因子陣的乘積,找出其元素之間對應的關系,即
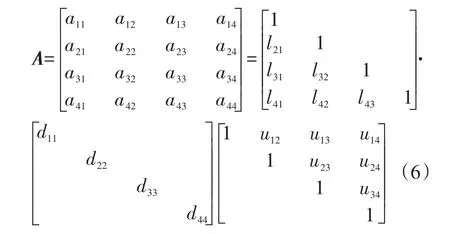
將L、D、U因子陣相乘并與A陣各元素相比較,轉換后可得L、D、U因子陣元素與A陣元素的關系如圖1中LDU合成陣所示。
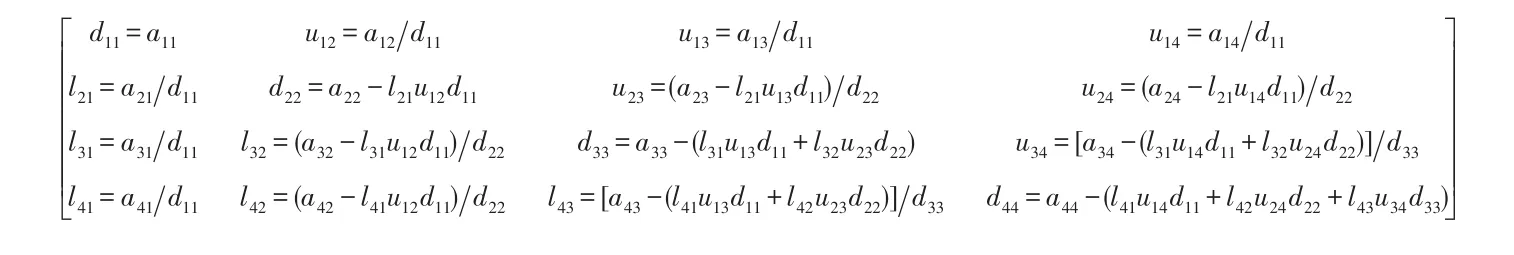
圖1 L、D、U因子陣元素與A陣元素的關系Fig.1 Relationships among the elements in L,D and U and those in A
圖1中雖然L、U因子陣的對角元素lii(=1)、uii(=1)與dii元素重合,但并不影響前代和回代計算。圖1的合成陣就是快速LDU法的基礎。
根據(jù)圖1,可以按列消元方式對A陣進行LDU三角分解后合成陣中各元素的計算,而這些計算公式與式(3)~式(5)完全相同,這說明圖1的合成陣體現(xiàn)了傳統(tǒng)LDU法的全部內(nèi)容,但合成陣的應用使得快速LDU法比傳統(tǒng)LDU法的計算過程更簡單易解。然而,此時的快速LDU法計算所有元素所要求的元素個數(shù)與傳統(tǒng)LDU法相同,因此其計算速度還不存在差異。
根據(jù)LDU合成陣,可歸納快速LDU法有以下幾個特點。
(1)可以按列消元法方式對A陣進行LDU三角分解,在A陣的基礎上直接形成LDU合成陣,只需1個數(shù)組。
(2)lji、dii和uij元素在同一個合成陣中,雖然lii、uii與dii元素重合,但并不影響前代和回代計算。前代過程由lji和dii元素完成,回代過程由uij元素完成。
(3)合成陣中l(wèi)ji、uij元素在任何情況下均有規(guī)律性的對應關系:如lji=uij,且其非零元素的位置對稱。因此在三角分解過程中,計算對角元以右非零的uij元素,可直接得到對角元以下非零的lji元素,從而省去對非零的lji元素的計算。
(4)以按列消元方式分步計算合成陣中l(wèi)ji、dii、uij元素,即對合成陣中同一行l(wèi)ji、dii、uij元素的計算類似于對對角元左側的lji元素逐個進行消元。由于所有元素均是分步計算得到,因此可稱其為過程法。過程法無需使用任何計算公式、簡單易解,特別方便程序編寫。但更重要的是在過程法中,可適當改變計算順序而獲得更高的計算效率。
根據(jù)合成陣中l(wèi)ji、dii、uij元素結構的特點,為進一步提高計算效率,規(guī)定計算過程如下。
(1)以“逐行規(guī)格化,按列消元”方式,先對第i行對角元以右的元素規(guī)格化得uij元素,但uij元素并不馬上賦值給對角元素以下相應的lji元素,或者lji′元素(也就是元素)暫不除該列的對角元dii,即此時的lji元素只是lji′元素。
(2)對第i列的lji′元素進行消元,得其右側的所有計算元素
(3)消元完成后再將第i行的uij元素賦值給第i列的lji元素,或用對角元dii除lji′元素得lji元素。

表1 公式法與過程法計算元素所需元素個數(shù)的比較Tab.1 Comparison of the number of required elements between the calculation formula and the proposed method
通過公式法與過程法計算元素所需元素個數(shù)的比較,在對lji′右側的元素進行消元計算時所用的元素數(shù)量方面,上述過程可省去約40%所需元素個數(shù)。大大提高計算效率。這種計算方式只有在快速LDU法中容易實現(xiàn),而在公式法中不易。
3 四角規(guī)則
盡管快速LDU法的應用非常簡單,但在實際編程過程中應用式(3)~式(5)并不方便。故提出直接用LDU合成陣元素進行計算的四角規(guī)則。采用四角規(guī)則對圖1中LDU合成陣各元素的計算過程進行分析。
1)第1次計算
第1次計算是對圖2中陰影部分進行計算,過程如下:
(1)對第1行元素規(guī)格化,得到第1行的u1j元素,而對角元以下的元素仍為lj1′;

圖2 第1次計算Fig.2 First calculation
(2)對第1列的lj1′元素消元,得其右側所有計算元素,但除d22外,其余元素均未完成計算,即還未轉換成相應的lji、dii、uij元素。
2)第2次計算
第2次計算是對圖3中陰影部分進行計算,過程如下:
(1)將第1行的u1j元素賦值給第1列相應的lj1元素,或用d11除lj1′元素得相應的lj1元素;
(2)對第2行元素規(guī)格化,得到第2行的u2j元素,而對角元以下的元素仍為lj2′;
(3)對第2列的lj2′元素消元,得到其右側所有計算元素,但除d33外,其余元素均未完成計算。

圖3 第2次計算Fig.3 Second calculation
3)第3次計算
第3次計算對圖4中陰影部分進行計算,過程如下:
(1)將第2行的u2j元素賦值給第2列相應的lj2元素,或用d22除lj2′元素得相應的lj2元素;
(2)對第3行元素規(guī)格化,得到第3行的u34元素,而對角元以下的元素仍為l43′;
(3)對第3列的l43′元素消元,得到d44。

圖4 第3次計算Fig.4 Third calculation
4)第4次計算
第4次計算將第3行的u34元素賦值給第3列的l43元素,或用d33除l43′元素得l43元素,完成計算。

圖5 第4次計算Fig.5 Fourth calculation
根據(jù)圖2~圖5,合成陣各元素的計算過程可簡化如下。
步驟1對第i行元素規(guī)格化得uij元素。
步驟2對第i列的lji′元素消元,得其右側的所有計算元素
步驟3將第i行的uij元素賦值給第i列的lji元素,或用對角元dii除lji′元素得lji元素。
步驟4依次循環(huán),完成所有計算。
步驟2中參加計算的元素在合成陣中的位置始終如圖6所示。圖中dii為對角元素;uik為交叉元素,位于對角元素同行以右;lji′(lji)為消元元素,位于對角元素同列以下,括號外(內(nèi))為賦值前(后)的值;為計算元素,位于消元元素所在行右側與交叉元素所在列的交互點上,分步完成計算后根據(jù)其所在位置轉化成相應的dii、lji′(lji)、uik元素,括號外(內(nèi))為計算前(后)的值。
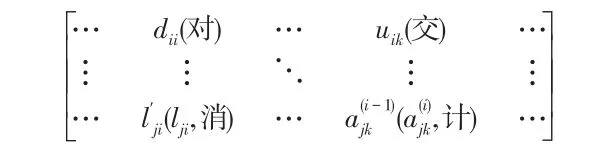
圖6 參加計算的元素在合成陣中的位置Fig.6 Positions of the calculated elements in the synthetic matrix
根據(jù)圖6可以看出,在合成陣元素的計算過程中,每次與計算有關的4個元素均在不同矩形的4個角上,因此將這種計算方法稱為四角規(guī)則。由于計算等式為即實際計算中只用除對角元外的3個元素,所以可將該計算過程看成是規(guī)格化后的消元計算。
由于四角規(guī)則的計算結果與式(3)~式(5)的結果完全一致,因此形成LDU合成陣的過程根本無需使用式(3)~式(5),而用四角規(guī)則以“逐行規(guī)格化,按列消元”方式可更快、更簡單地計算出LDU合成陣的所有元素,并使三角分解過程計算程序的編寫變得極為簡單直觀。
4 計算舉例
表2給出公式法與過程法對IEEE-30、IEEE-57、IEEE-118節(jié)點系統(tǒng)的復數(shù)導納矩陣Y在不考慮元素稀疏性時進行三角分解所需時間的比較。表中t1為公式法對A陣進行三角分解所需時間;t2為過程法對A陣進行三角分解所需時間,消元完成后對lji′元素進行l(wèi)ji=lji′/dii計算;t3為過程法對A陣進行三角分解所需時間,消元完成后直接將uij元素賦值給lji元素。
從表2可以看出,對IEEE-30、IEEE-57、IEEE-118節(jié)點系統(tǒng),過程法均比公式法快約55%,但消元計算后直接將uij元素賦值給lji元素所需時間比對每個lji′元素進行l(wèi)ij=lji′/dii計算所需時間還要少2%~4%,主要由于除法計算比賦值語句需要更多的計算時間。
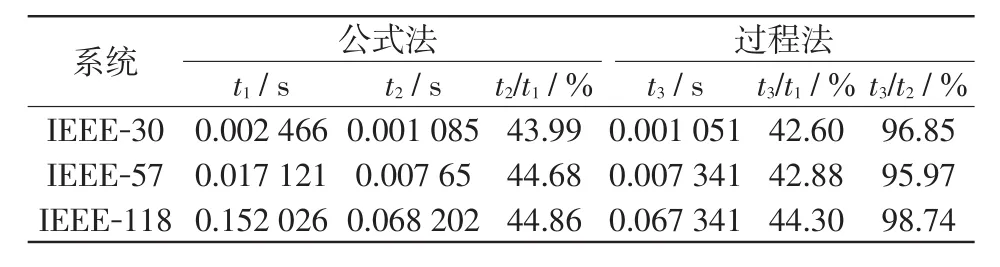
表2 公式法與過程法對三角分解法所需時間的比較Tab.2 Comparison of the required time for the triangular factorization algorithm between calculation formula and process method
5 結 語
本文針對傳統(tǒng)LDU法中的諸多不便,提出快速LDU法。在快速LDU法中,引入了合成陣的概念,將L、D、U因子陣元素直接計算后存放在原A陣數(shù)組中。合成陣清晰地表明了lji、dii和uij元素關系,應用“逐行規(guī)格化,按列消元”方式,可簡單地用四角規(guī)則分步計算L、D、U因子陣的元素,而無需使用繁瑣的計算公式。改變元素的計算過程,可大大減少計算所需元素的總數(shù),從而大大提高編程及計算效率。對IEEE-30、IEEE-57、IEEE-118節(jié)點系統(tǒng)編程計算,過程法均比公式法快約55%,且快速LDU法為進一步簡化各種三角分解法奠定了良好的基礎。
[1]關根泰次.電力系統(tǒng)潮流計算[M].日本:電氣書院,1971.
[2]陳珩.電力系統(tǒng)穩(wěn)態(tài)分析[M].3版.北京:中國電力出版社,2007.
[3]王祖佑.電力系統(tǒng)穩(wěn)態(tài)運行計算機分析[M].上海:水利電力出版社,1987.
[4]王艷天(Wang Yantian).解線性方程組的LU分解法(LU decomposition method for solving linear equations)[J].科技創(chuàng)新導報(Science and Technology Innovation Herald),2009(4):245-245.
[5]Hadi Saadat.Power System Analysis[M].New York:Mcgraw-Hill International Editions,1999.
[6]西安交通大學,清華大學,浙江大學等.電力系統(tǒng)計算[M].北京:水利電力出版社,1978.
[7]曾祥金,吳華安.矩陣分析及其應用[M].武漢:武漢大學出版社,2007.
[8]周全仁,張清益.電子計算機在電網(wǎng)計算機中的應用—電網(wǎng)計算與常用程序[M].湖南:湖南科學技術出版社,1983.
[9]陳永琳.電力系統(tǒng)繼電保護的計算機整定計算[M].北京:水利電力出版社,1994.
[10]錢煥延,趙曉彬.計算方法[M].西安:西安電子科技大學出版社,1990.
[11]何仰贊,溫增銀.電力系統(tǒng)分析[M].3版.武漢:華中科技大學出版社,2002.
[12]周杰.矩陣分析及其應用[M].四川:四川大學出版社,2008.
[13]李慶楊,王能超,易大義.數(shù)值分析[M].5版.北京:清華大學出版社,2008.
[14]邱曉燕,劉天琪.電力系統(tǒng)分析的計算機算法[M].北京:中國電力出版社,2009.
[15]張伯明.高等電力網(wǎng)絡分析[M].2版.北京:清華大學出版社,2007.
[16]馮天民,劉寶柱,鮑海(Feng Tianmin,Liu Baozhu,Bao Hai).一類含CCCS網(wǎng)絡形成節(jié)點阻抗矩陣的新算法(A novel algorithm for building Z-matrix of electric power network including CCCS)[J].電工技術學報(Transactions of China Electrotechnical Society),2009,24(2):139-144.
[17]楊美佳,劉寶柱(Yang Meijia,Liu Baozhu).針對大量接地支路電網(wǎng)形成節(jié)點阻抗矩陣的改進算法(An improved algorithm for forming Z-matrix of power grid containing large amount of grounded-branches)[J].電力系統(tǒng)保護與控制(Power System Protection and Control),2010,38(22):161-165.
[18]朱永利,宋少群,馮建衡(Zhu Yongli,Song Shaoqun,F(xiàn)eng Jianheng).互聯(lián)電網(wǎng)節(jié)點阻抗陣實時修改與邊界等值化簡的并行計算方法(A parallel algorithm of realtime modification and boundary equivalents of impedance matrices of interconnected networks)[J].電工技術學報(Transactions of China Electrotechnical Society),2007,22(9):167-173.
[19]任麗娜,陳軍(Ren Lina,Chen Jun).雙復數(shù)阻抗矩陣節(jié)點導納法實現(xiàn)低壓短路電流計算(Double complex impedance matrix node admittance method to achieve low voltage circuit current calculation)[J].電氣應用(Electrotechnical Application),2009,28(1):56-61.
[20]樂全明,郁惟鏞,杜俊紅(Yue Quanming,Yu Weiyong,Du Junhong).一種形成節(jié)點阻抗矩陣的改進算法(An improved novel algorithm for building Z-matrix)[J].中國電機工程學報(Proceedings of the CSEE),2005,25(2):34-39.
[21]賴永生,劉明波,陳燕梅(Lai Yongsheng,Liu Mingbo,Chen Yanmei).大規(guī)模電網(wǎng)的動態(tài)無功優(yōu)化算法(Algorithm for dynamic reactive power optimization problem in large power grid)[J].電力系統(tǒng)及其自動化學報(Proceedings of the CSU-EPSA),2012,24(5):7-12.
[22]聶永輝,肖白,劉鳳蘭(Nie Yonghui,Xiao Bai,Liu Fenglan).電力系統(tǒng)最優(yōu)潮流新模型及其內(nèi)點法實現(xiàn)(New optimal power flow model and its solution by using nonlinear interior point method)[J].電力系統(tǒng)及其自動化學報(Proceedings of the CSU-EPSA),2014,26(11):53-57.
[23]初壯,于群英,李笑薇(Chu Zhuang,Yu Qunying,Li Xiaowei).求解含小阻抗支路配電網(wǎng)潮流的牛頓法(Newton method for solving power flow of distribution networks with small impedance branches)[J].電力系統(tǒng)及其自動化學報(Proceedings of the CSU-EPSA),2016,28(9):36-41.
Study on Fast LDU Triangular Factorization Algorithm
XI Xiaoqing,LU Jiehuan,ZHUANG Guangyu,CHEN Ken
(School of Information Engineering,Nanchang University,Nanchang 330031,China)
Since the relationship among the elements in factor matricesL,DandUis not clear,the calculation process of the conventionalLDUtriangular factorization algorithm is complicated and hard to understand.Besides,the number of storage units and the corresponding calculation load become larger.To solve the above problems,a fastLDUtriangular factorization algorithm is presented in this paper.The introduced synthetic matrix can reflect the relationship among the elements inL,DandU,and reduce the number of storage units obviously.By applying the principle of“Normalization by rows and elimination by columns”as well as the Four-angle Rule,triangular factorization can be completed without relying on the calculation formulas.Moreover,with a new calculation process,the total number of required elements can be reduced obviously.The proposed algorithm is proved to be efficient and practical by programming and calculation on different IEEE node systems.The proposed algorithm can be used to fast solve the constant coefficient linear equations in power systems and other engineering fields.
linear equation;LDUtriangular factorization algorithm;Gaussian elimination;normalization;four-angle rule;power system
TM315
A
1003-8930(2017)10-0118-05
10.3969/j.issn.1003-8930.2017.10.020
2016-03-09;
2017-06-29
陳 懇(1956—),男,博士,教授,研究方向為電力系統(tǒng)穩(wěn)態(tài)分析及優(yōu)化。E-mail:2494337178@qq.com
席小青(1991—),女,碩士研究生,研究方向為電力系統(tǒng)穩(wěn)態(tài)分析及優(yōu)化。Email:1164565914@qq.com
陸節(jié)渙(1991—),男,碩士研究生,研究方向為電力系統(tǒng)穩(wěn)態(tài)分析及優(yōu)化。Email:357447051@qq.com
莊廣宇(1991—),男,碩士研究生,研究方向為電力系統(tǒng)穩(wěn)態(tài)分析及優(yōu)化。Email:1615206374@qq.com

