基于Workbench的濃密機中心軸吊點位置的優化

關玉明，于 盼，李 朝，崔 佳，商 鵬

（河北工業大學 機械工程學院，天津 300130）

基于Workbench的濃密機中心軸吊點位置的優化

關玉明，于 盼，李 朝，崔 佳，商 鵬

（河北工業大學 機械工程學院，天津 300130）

針對中心傳動式濃密機的中心軸整體變形、等效應變和最大應力較大的情況，介紹了一種基于Workbench優化技術進行中心軸吊點位置選取的方法.對中心軸進行受力分析，定義優化變量，將整體變形、等效應變和最大應力作為目標函數，基于Workbench的不斷迭代計算得出幾種優化方案和目標函數曲線圖，經比較選出合適的方案，并對選取的方案做了進一步的驗證.結果表明，優化后的整體變形、等效應變和最大應力有了顯著的改善.

Workbench優化；中心軸；吊點位置；整體變形；等效應變；最大應力

濃密機是基于重力沉降作用的固液分離設備，通常為由混凝土、木材或金屬焊接板作為結構材料建成帶錐底的圓筒形淺槽，可將含固量為10%～20%的礦漿通過重力沉降濃縮為含固量為45%～55%的底流礦漿.本文討論的濃密機為中心傳動式，由液壓馬達驅動，動力通過減速器后傳至中心軸使其轉動，并帶動安裝在中心軸上的耙架也隨之轉動，這樣便可攪動礦漿.在運動過程中，漿料被攪動時所產生的扭矩直接作用在耙架上，造成中心軸應發生整體變形，這對中心軸的設計帶來了一定的困擾.因此，在設計中心軸時，研究合理的耙架吊點位置使得中心軸吊點處的整體變形、等效應變以及最大應力達到最優是十分必要的.

隨著計算機技術的飛速發展，結構優化算法也取得了很大的發展，目前結構優化經歷了較低層次的尺寸優化，較高層次的結構形式優化和如今更高層次的拓撲優化.李純金等[1]利用遺傳算法，對隨車起重機折疊臂架鉸點位置進行了優化，不但降低了液壓缸在工作過程中所受到的最大值，而且使整個液壓系統壓力更趨于穩定；王琪等[2]利用粒子群算法，對雙層剪式液壓升降臺液壓缸位置進行仿真優化分析，使升降臺升降更加平穩，很好地改善了其工作性能，大大提高了其使用壽命.侯忠明等[3]在ADAMS中建立參數化伸縮臂叉車模型，利用設計研究及試驗設計功能對連桿變幅機構進行參數化分析，找到最優鉸點位置，使得液壓缸最大受力減小，實現了優化目標.曾剛[4]通過Pro/E軟件中的優化設計功能對煤礦廠給料機的定位尺寸進行優化，使得更多的物料能以自溜的方式進入給料機，從而減少了地面鏟車的數量及工作量，節約了成本.本文中主要針對中心軸與耙架的吊點位置建立數學模型，借助Workbench尋找最優解，得出吊點的最優位置，以達到優化的目的.

1 靜力學分析

本文討論的新型濃密機為中心傳動式，中心軸與耙架的安裝關系如圖1所示，在濃密池的正中央安有一根中心軸1，中心軸的末端固定有一個十字形耙架，耙架有長短耙架之分，2組耙架對稱地安裝在中心軸上，耙架的下端裝有刮板，耙架與地面成9°角.

1.1 力學模型的建立

由于耙架對稱安裝，長短耙架的吊點位置位于同一水平高度，為了提高軟件的運算效率，本文以一端耙架的吊點位置為主進行分析計算.圖2為中心軸與耙架的機構簡圖，以O點為坐標原點，吊點處為A，在Y軸上，A點坐標記為（0，d），短耙架吊點處為B，記為（xB，yB）=（5.685，1.641），OB與Y軸夾角為81°，AB與X軸的夾角記為θ.濃密機工作時，耙及耙架需要克服漿液對其產生的扭矩T1.

由圖2可以看出中心軸吊點處的拉力與短耙架吊點處的拉力互為一對作用力與反作用力.因此，可利用短耙架的求解來計算中心軸吊點處的受力.對中心軸和短耙架進行靜力學分析得：

式中：T為驅動裝置對中心軸的扭矩，N·m；T1為漿液對短耙架整體的最大扭矩，N·m；F為中心軸吊點處的處所受到的拉力，N；F′為短耙架吊點處所受到的拉力，N.

1.2 短耙架靜力學分析

漿液對短耙架整體的最大扭矩T1可以認為是由耙架所受的扭矩TZ與耙所受的扭矩Tl疊加作用產生[5]，即

1） 耙架扭矩分析

耙架和耙轉動范圍的漿液濃度較低，該區域漿液按流體分析.耙架與中心軸相連，其運動軌跡是圓柱體，如圖3所示.耙架在運動過程中要克服漿液對其的屈服應力和周圍一定區域內漿液對其的剪切應力，因此，耙架所受到的扭矩TZ是剪切圓柱體側面的扭矩Ts和上下端面的扭矩Te的總和[5].將扭矩表示為剪力的函數為：

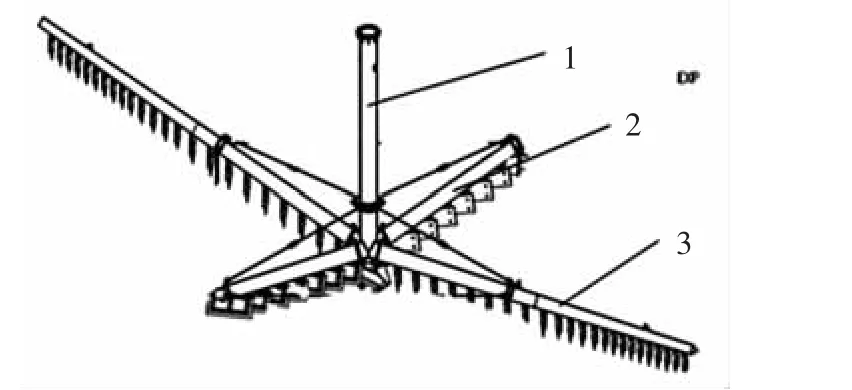
圖1 中心傳動式濃密機傳動件模型圖Fig.1 The model of the transmission part of the central drive thickener

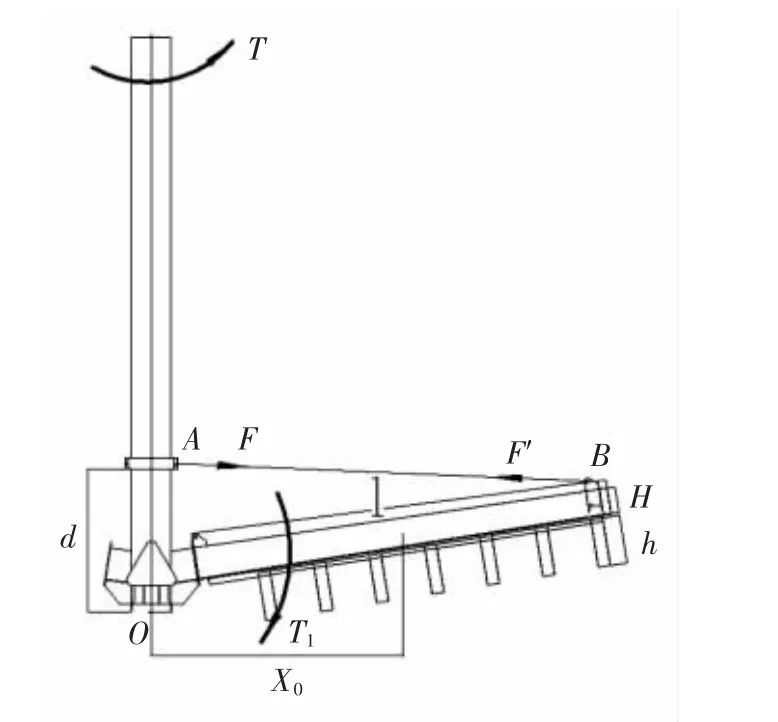
圖2 中心軸與耙架的機構簡圖Fig.2 Schematic diagram of the central shaft and harrow frame

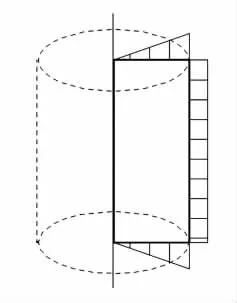
圖3 耙架運動軌跡及應力分布Fig.3 Track and stress distribution of the harrow frame

式中：τs為耙架側面處的剪切應力，Pa；τe為耙架上下端面處的屈服應力，Pa；l為耙架的長度，m，l=5.917 m；r為剪切圓柱體的半徑，m，r=lcos81°；δ為剪切圓柱體的高度，m，δ=H=0.303 m.

由于耙架接觸部分流動的漿液濃度基本相同，而且耙架高度不大，因此認為耙架上下端面以及側面所受剪切應力大小相等，如圖3所示，即耙架所受剪切應力為τ0=τs=τe=50 Pa[6-7].

2） 耙的扭矩分析

耙的運動軌跡是圓環體，如圖4所示，因此會產生內外圓面和上下端面4個剪切面.由于耙與耙架相連，在對耙架進行分析時，已經對圓環體的上端面進行了分析，所以在這里省去這一部分的計算.耙運動時的最大扭矩表示為屈服應力的函數為

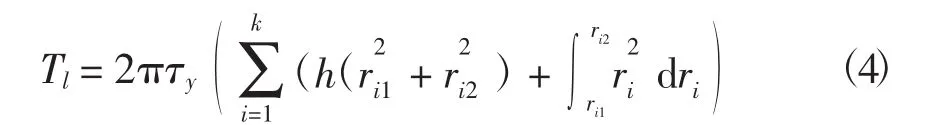
式中：τy為耙的屈服應力，Pa，τy=50 Pa；h為耙的高度，m，h=0.6m；k為耙的個數，k=7；ri1和ri2分別為第i個剪切內圓柱面與外圓柱面的半徑，m.

根據以上分析，可以得出漿液對短耙架整體的最大扭矩T1的應力函數表達式

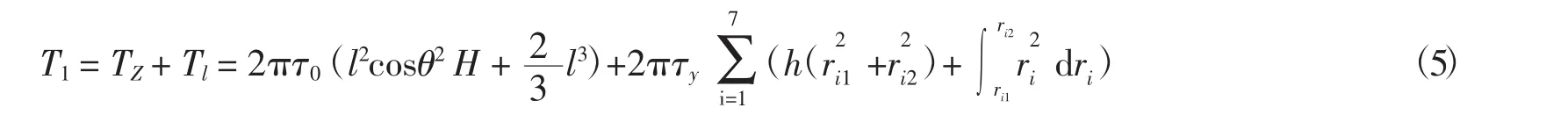
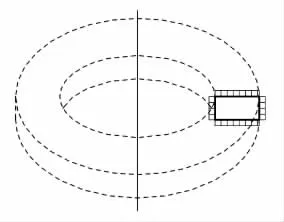
圖4 耙運動軌跡及應力分布Fig.4 Trajectory and stress distribution of harrow

短耙架受力分析如圖5所示.對其進行靜力學分析，得出如下方程組：

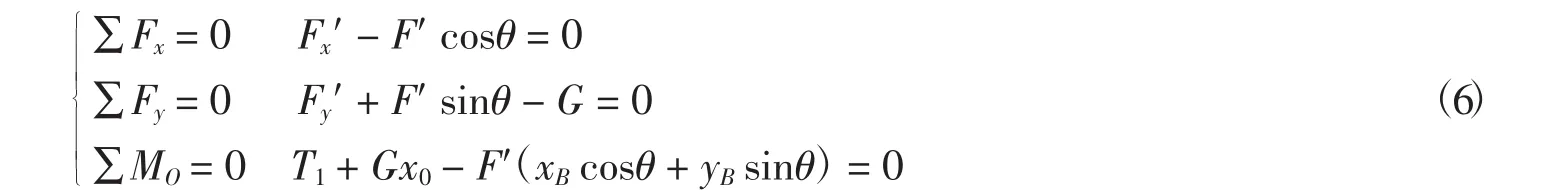
式中：F′為鉸點處的作用力，N；G為短耙架與耙的重力，N，G=2 038 N；x0為耙架與耙的質量中心，m，x0=3.098m；θ為拉桿與x軸的夾角，cosθ=0.999 1，sinθ=0.02.

聯立式（1） ～式（6），計算得出中心軸受到來自驅動的扭矩T=82 100 N·m，中心軸鉸點出的拉力F=15 472 N.

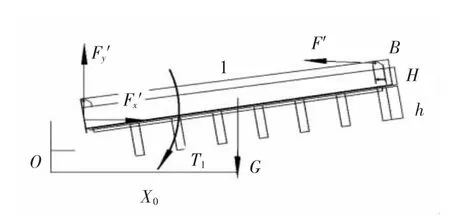
圖5 短耙架受力分析圖Fig.5 Force analysis of short frame

2 ANSYS Workbench優化設計

ANSYS Workbench是利用APDL（參數化設計語言）對結構設計的參數進行調整，它要求優化的模型必須為參數化模型.優化的是通過算法不斷的循環“分析——評估——修正”[8]來實現的.ANSYS優化模塊中常用的算法有零階法、一階法、隨機搜索法、最有梯度法[9]，其中，隨機搜索法完成指定次數的迭代分析，可以合理確定優化空間[10-11]，是零階法和一階法的其前期處理步驟；零階法通過隨機搜索建立狀態變量，使其與目標函數逐步逼近，廣泛適用于各類工程問題，但是其收斂速度較慢[12]；一階法的結果準確，但是計算量大，容易陷入局部最優解.

綜合考慮各種優化算法的特點，本次優化設計決定使用零階法優化算法對模型進行求解運算.

圖6是中心軸的三維模型圖，為了提高運行效率，在建模過程中對模型進行了簡化，忽略了一些局部特征.中心軸的外形尺寸為：長度7 110 mm，直徑457 mm.

使用Workbench對原有中心軸進行分析，得出如圖7所示整體變形云圖.中心軸在啟動瞬時所受到的扭矩最大，因此研究在該時刻中心軸的整體變形是有必要的.由圖7可以看出，中心軸最大變形量達到0.001 239 2 m，位于與減速器連接的部位，在結構改進時應保證具有較小的整體變形量.

圖6 中心軸模型圖Fig.6 Central axis model

2.1 參數化建模

參數化建模基本步驟如下.

1） 定義材料屬性.中心軸的材料為Q235，材料屬性見表1.

2）施加約束條件.中心軸受到來自驅動的扭矩T=82 100 N·m和吊點處的拉力F=15 472 N，在Workbench施加力時將拉力分解為Y軸和X軸的力Fx=-15 458 N，Fy=-309 N（說明：負號表示力的方向與坐標軸正方向相反）.

3） 網格劃分.由于中心軸尺寸較大，結構復雜，為了提高運算效率，設置Sizing（單元尺寸）為Medium.劃分網格設置完成后，中心軸被劃分為73 509個節點，33 060個有限單元.

4） 參數化設置.參數化設置見表2.

表2 鉸點處參數化設置Tab.2 Parameterized setting of hinge points

2.2 結果分析

利用Workbench進行結構優化，根據各變量取值范圍，優化軟件進行迭代計算得到12個設計點方案，計算得出整體變形對設計點的曲線圖8a）、最大應力對設計點的關系曲線圖8b）和等效應變對設計點的曲線圖8c） .

由圖8a）可以看出，在設計點2處，中心軸的整體變形達到最小，因此將設計點2作為一個候選點.由圖8b）和圖8c）可以看出，在設計點7處等效應變和最大應力均達到最小值，因此將設計點7作為一個候選點；另外，等效應變和最大應力對設計點的曲線最后都收斂于設計點12，表明Workbench將設計點12作為最優方案，因此將設計點12也作為一個候選點.綜合分析圖8可以得出3個設計點，各自優化后的數據如表3所示.

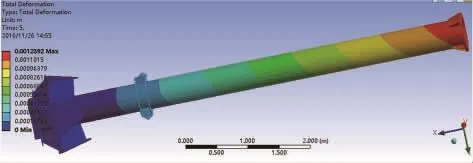
圖7 原有中心軸整體變形云圖Fig.7 Overall deformation of the original central axis

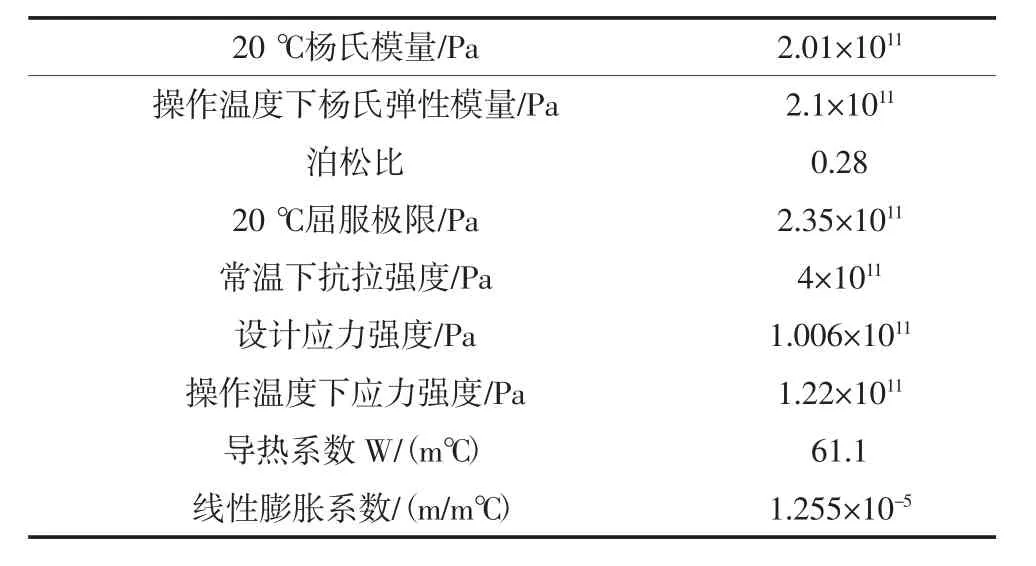
表1 Q235材料屬性表Tab.1 Q235 material properties table

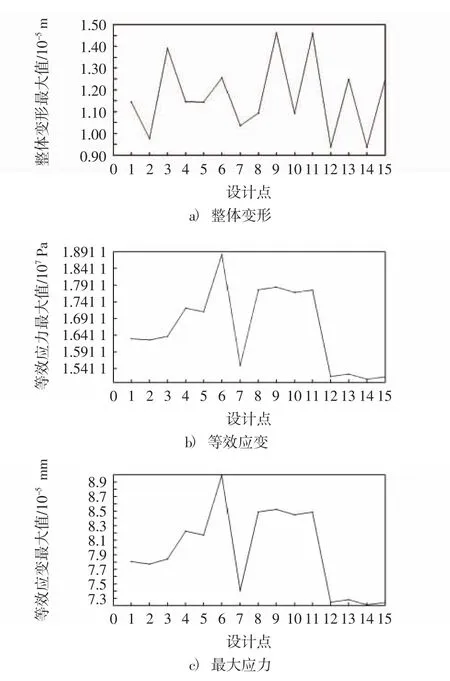
圖8 目標變量對設計點的曲線圖Fig.8 The curve of the target variable to the design point

根據表3數據可以看出，設計點12處的綜合效果更優，因此選擇設計點12作為本次優化的方案.

由圖9可以看出，優化后的吊點拉力明顯降低，整體變形量的最大值減小了24%，等效應變減小了31%，最大應力減小了31%，這顯著提升了中心軸的工作穩定性.

3 總結

使用ANSYS Workbench對濃密機中心軸吊點位置在滿足使用要求的情況下進行了整體變形、等效應變和最大應力最小值的優化設計，在得出的方案中根據實際要求選取了最佳方案，并進一步證明了方案的可行性.同時，也證明了使用ANSYS Workbench對結構進行優化的方法是可行的.這種優化方法操作簡單，計算快捷，為結構優化提供了新的方法.

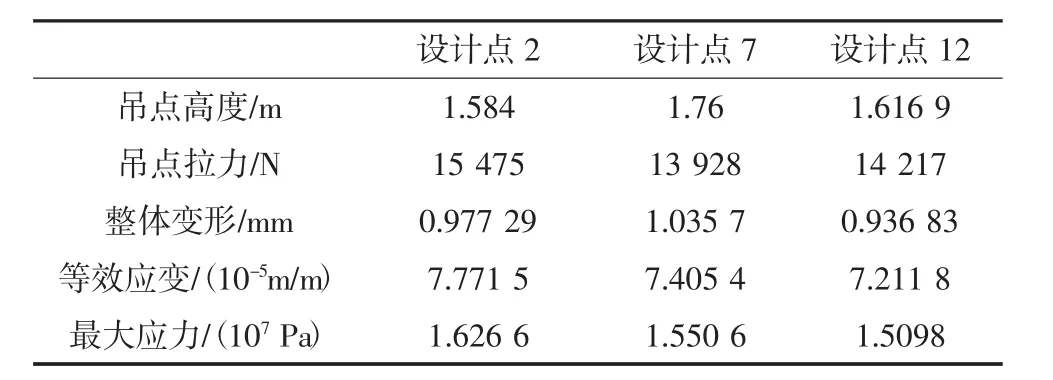
表3 優化設計點Tab.3 Optimal design points

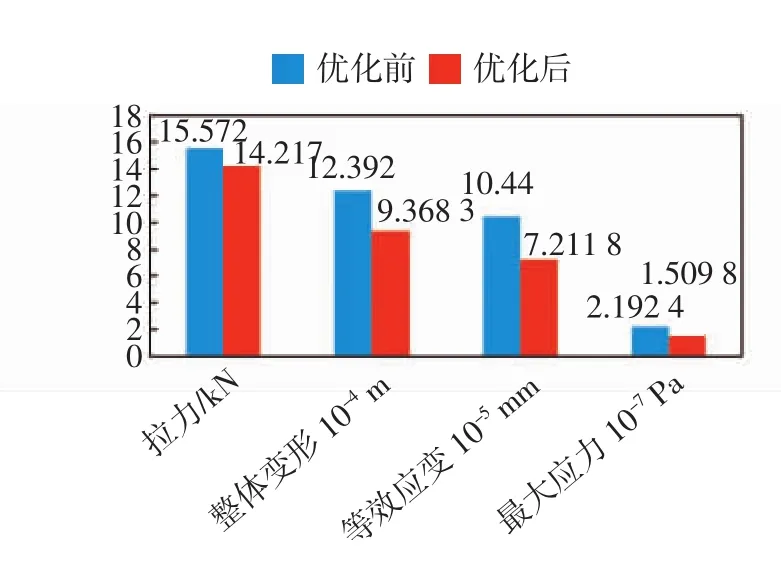
圖9 優化前后數據對比Fig.9 Comparison of data before and after optimization

[1] 李純金，褚月橋，周海波.基于遺傳算法隨車起重機折疊臂架鉸點位置優化[J].江蘇科技大學學報（自然科學版），2014，28（1）：30-36.

[2] 王琪，張任，劉建，等.基于粒子群算法的雙層剪式液壓升降臺液壓缸位置的多目標優化問題研究[J].機械科學與技術，2015，34（8）：1229-1234.

[3] 侯忠明，王勝軍，辛濤.基于ADAMS的伸縮臂叉車鉸點位置優化設計[J].起重運輸機械，2009，23（6）：42－44.

[4] 曾剛.基于Pro/E的堆煤場給料機位置優化設計[J].煤礦技術，2014，33（10）：200-201.

[5] 吳愛祥，焦華喆，王洪江，等.深錐濃密機攪拌刮泥耙扭矩力學模型[J].中南大學學報（自然科學版），2012，43（4）：1469-1474.

[6] 李輝，王洪江，吳愛祥，等.基于尾砂沉降與流變特性的深錐濃密機壓耙分析[J].北京科技大學學報，2013，35（12）：1553-1558.

[7] 王勇，王洪江，吳愛祥.基于高徑比的深錐濃密機底流濃度數學模型[J].武漢理工大學學報，2011，33（8）：113-117.

[8] 徐釗，錢作勤，張平，等.基于ANSYS優化技術的換熱器法蘭的結構設計[J].石油和化工設備，2009（6）：15-18.

[9] 夏衛明，駱桂林，嵇寬斌.ANSYS優化算法的研究及其在液壓機優化設計中的應用[J].鍛壓裝備與制造技術，2010（1）：43-47.

[10]陸山，魯馮杰.基于ANSYS的整體葉盤結構優化設計[J].航空動力學報，2012，27（6）：1218-1224.

[11]李倫未，陸山.基于ANSYS的多輻板風扇盤結構優化設計技術[J].航空動力學報，2011，26（10）：2245-2250.

[12]寇劍鋒，鄭錫濤，彭興國.基于零階優化方法的無人機復合材料進氣道結構優化與分析[J].機械強度，2008，30（6）：1018-1022.

Optimization of hanging point position of thickener center shaft based on Workbench

GUAN Yuming,YU Pan,LI Zhao,CUI Jia,SHANG Peng

（School of Mechanical Engineering,Hebei University of Technology,Tianjin 300130,China）

A method for the selection of the hanging point position of the center shaft based on the Workbench optimization technique is introduced on the matter of the center shaft of the central drive thickener,such as the total deformation,the equivalent strain and the equivalent stress maximum.Force analyses are conducted on the center shaft and the optimization variables are defined.Put the total deformation,the equivalent strain and the equivalent stress maximum as the output variables.Several optimization schemes and the diagrams of the hinge point position with the optimization goal are obtained through the continuous iterative calculation of Workbench.The optimal scheme is chosen in accordance with the chart.Finally,further validation of the selected scheme is made.The results show that there is a big improvement in the optimization of the total deformation,the equivalent strain and the equivalent stress maximum.

Workbench optimization;center shaft;hinge position;the total deformation;the equivalent strain;the equivalent stress maximum

TH133.2

A

1007-2373（2017） 05-0028-05

10.14081/j.cnki.hgdxb.2017.05.005

2017-03-28

天津市科技特派員項目（14JCTPJC00532）

關玉明（1957-），男，教授，gyuming@163.com.

[責任編輯 楊 屹]