微觀量子器件中分子馬達單向轉動的條件機理研究

宋亞峰，朱勤生，焦壯壯，孔雄雄，李輝杰

(1. 商洛學院 電子信息與電氣工程學院物理系，陜西 商州 726000； 2. 中國科學院半導體研究所材料重點實驗室，北京 100083)

微觀量子器件中分子馬達單向轉動的條件機理研究

宋亞峰1，朱勤生2，焦壯壯1，孔雄雄1，李輝杰2

(1. 商洛學院 電子信息與電氣工程學院物理系，陜西 商州 726000； 2. 中國科學院半導體研究所材料重點實驗室，北京 100083)

微觀量子器件中的分子馬達是微觀機械系統與納米器件領域的重要器件，深入系統地研究了其單向轉動的條件及機理。先從幾何的角度分析了宏觀棘輪工作的物理本質，得出了3個必要條件。之后開始討論微觀棘輪，將熱漲落對其的影響歸在第3個條件。接著具體分析了溫度T較低、T較高無外界作用、T較高有較大外界作用3種情形下的不同機理。著重分析了第3種情形下斜面特性是如何實現對原本無極性的外界作用進行了“整流”。最后得出微觀棘輪單向轉動的兩個必要條件為：體系的非平衡性(內因)和存在適當的極性結構(外因)。這些結論可以為相關的微觀量子器件中的納米器件的設計及應用提供有益的參考。

分子馬達；棘輪；熱漲落；熱力學第二定律

近年來，隨著半導體微電子領域對微米向納米尺度的深入發展，一系列微觀尺度的量子器件應運而生。在各種微觀量子器件中，量子尺度的分子馬達越來越成為近年來一個持續的研究熱點[1-13]。微觀量子器件中的分子馬達是微觀機械系統與納米器件領域的重要器件，在微納機械電子器件系統中及量子生物物理領域有重要的應用前景。這其中，分子馬達在微觀領域轉動的單向“整流”特性尤其一直是影響其應用前景的一個非常重要的基本問題，因此引起了很多這方面的研究[3-8,12]。分子馬達的典型模型可以用微觀尺度的棘輪來描述，即所謂的費曼棘輪(Feynman’s 棘輪)[1]。對此我們進行了系統深入的分析和研究。

1 建模過程及結果分析

1.1宏觀棘輪的物理本質

我們對比圖1 a和b得棘輪單向轉動的必要條件1：棘輪齒形狀的不對稱性。由圖1c、圖2a得必要條件2：棘爪端部軌跡最低點A應低于棘輪內包絡圓最高點C。對比圖1 a、c和圖2b得必要條件3：彈簧原長時棘爪頂部P0點應位于棘輪的外包絡圓內，即棘輪和棘爪要具有直接接觸的機會。分析可知，條件2才是產生單向轉動的最本質的條件，可以認為，凡滿足條件2的機構都是廣義棘輪。但本文只討論圖1a所示的最一般意義上的棘輪，即狹義棘輪。對于宏觀棘輪來說，其發生單向轉動的必要條件一可以描述為環境的各向異性或軌道要提供穩定的極性。必要條件2、3可以歸納為發生了不可逆過程。

a本文所討論的棘輪；b“向日葵輪”；c一種可雙向轉動的棘輪結構

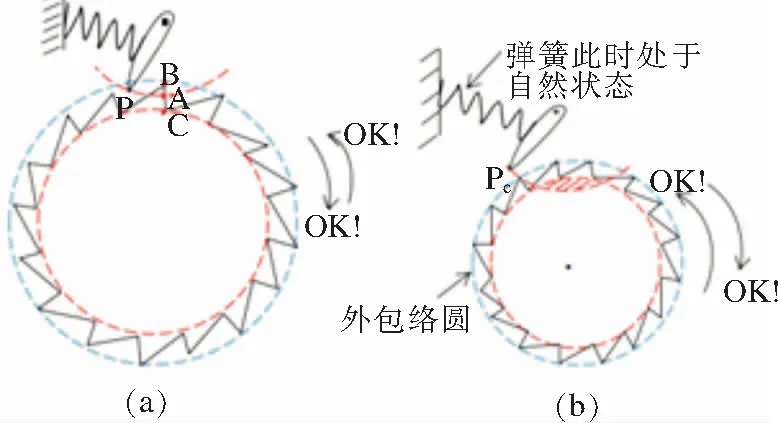
a另一種可雙向轉動的棘輪結構；b可以單向轉動的棘輪

1.2微觀量子尺度分子馬達基本情況分析

鑒于本文所要討論的分子馬達為圖1a所示的狹義棘輪，所以他應滿足必要條件1、2。我們知道，熱漲落對于分子馬達是不可避免的，這是與宏觀機器最大的不同之處。顯然熱漲落直接影響到棘爪頂端與棘輪齒之間的相對位置，即影響必要條件3是否滿足。因此，我們認為，熱漲落主要通過必要條件3來影響棘輪最終是否可以單向轉動。

具體來說，熱漲落主要影響兩點：提供讓棘輪正轉和反轉的原動力，并且正轉和反轉的幾率相等；使棘爪尖端P點上下跳躍。此處我們考慮的是理想情況：棘爪和棘輪的轉軸的相對距離是不變的，即圖1 a中的圓心距O1O2始終不變。

1.3分子馬達的3種情形

如圖3所示，我們把問題分為以下3種情形。

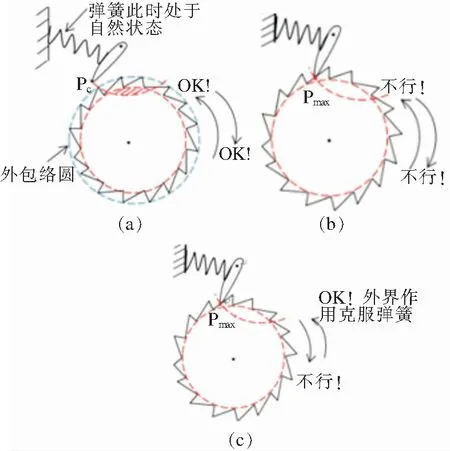
a 情形i，T較高; b 情形ii,T較低，無外界作用; c 情形iii,T較低，有較大外界作用

圖33種不同情形下的棘輪單向轉動分析

情形i(圖3a)溫度T較高時，熱漲落足以使P點在彈起足夠高，以致于P點到了棘輪的外包絡圓之外，并維持較長時間，相當于不滿足條件3(如圖3a)。顯然，棘輪可以自由正轉或反轉，凈效果是不會單向轉動(這一點可以通過T→∞來設想)。

情形ii(圖3b)T很低，且沒有外界作用時，熱漲落并不能使P點彈起足夠高，P點始終在棘輪的外包絡圓內，雖然滿足條件3，但條件1、2、3只是必要條件。由于此時T很低，系統能量很有限，既然不能使棘爪彈得足夠高，也就沒有理由是棘輪克服棘爪彈簧的“勢壘”而轉過一個齒。因為棘輪的漲落和棘爪的漲落在統計意義上是相對獨立的，二者并不沒有誰比誰更占優。而且二者本來就不可區分，因為熱平衡系統中只區分狀態不區分過程。因此此時實際上是棘輪棘爪被凍結了，系統的能量不足，棘輪連一個齒都轉不了，凈效果也是不會單向轉動(這一點可以通過T→0來設想)。

對比情形i和ii，我們知道，只要沒有外界作用(即體系處于平衡狀態)，無論T較高還是較低，棘輪都不會單向轉動。但其實二者的機理并不相同，前者是由于熱漲落使必要條件3不滿足，后者雖然3個條件都滿足，但能量不足，系統處于被凍結狀態。可以看到只要是熱平衡系統，光憑系統本身不會實現將熱不斷轉化成功而不引起其他變化的，這正是熱力學第二定律所描述的。

情形iii(圖3c)當T較低但有某種較大的外界作用中的外界作用時，外界可以提供棘輪轉動的額外動力，他使棘輪正、反轉的幾率是一樣的。但下面“四”中的分析將會看到，由于“單側斜面的幾何特性”對這個動力進行了“整流”，使棘輪想要反轉時出現自鎖，能量就耗散掉了；而當它想正轉時正好借助于斜面的作用實現正轉。凈效果就是棘輪實現了單向轉動。

對比情形ii和iii，可以看到正是由于iii中系統處于非平衡狀態，才使它現了單向轉動。

2 邏輯分析及舉例

為方便起見，我們將較高的溫度全記為T，較低的溫度記為t，例如出現T1，t2(則有T1>t2)。將圖4a和圖4b中的1、2點用理想桿(剛性絕熱)連接，即得費曼棘輪[1](圖4c)我們知道，后者能單向正轉。此時對比各圖，可知圖4c中的棘爪與圖3a中的溫度相同，圖4c中的葉輪與圖3c中的溫度相同；

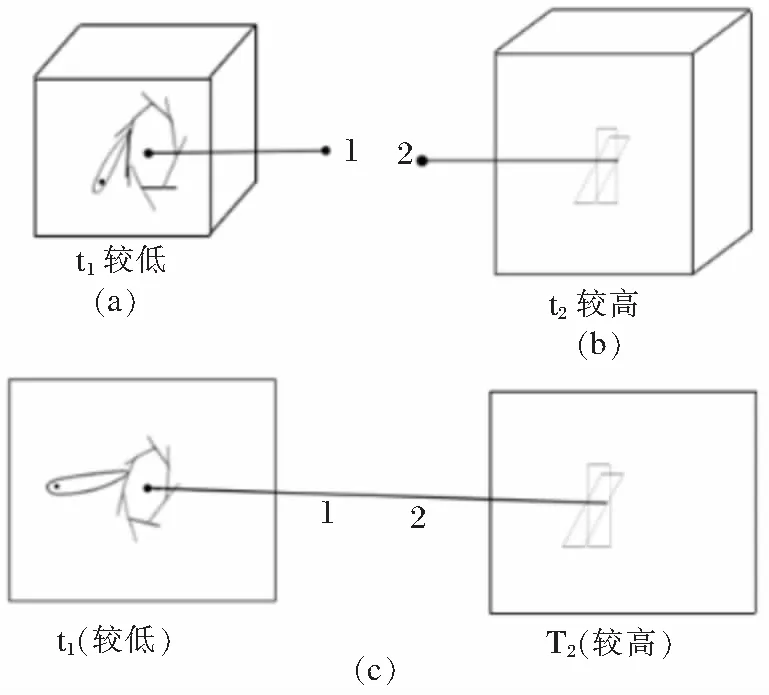
a棘輪不單向轉；b葉輪不單向轉；c棘輪正轉

而另一方面，可以近似地認為，由于理想桿的作用，圖4c中的棘輪和圖3c中的葉輪溫度相同，這樣，我們就得到實際上圖4c中的棘輪溫度為T2，棘爪溫度為t1，二者溫度并不相同，系統為非平衡狀態。相比之下，圖4a、b各自都是平衡系統。這一點是只有圖4c產生單向轉動的原因。因此可得微觀棘輪單向轉動的必要條件I(內因)：系統的非平衡性。

但是，是否系統具備非平衡性就一定會產生單向轉動呢？顯然不是。我們來看圖5和圖6。圖5的葉輪顯然不會單向轉動。由于圖中的葉輪及軸只起著機械連接的作用，并不傳導熱。所以當考慮系統變化非常緩慢的準靜態過程時很容易讓人誤以為系統可以看成是可逆過程。

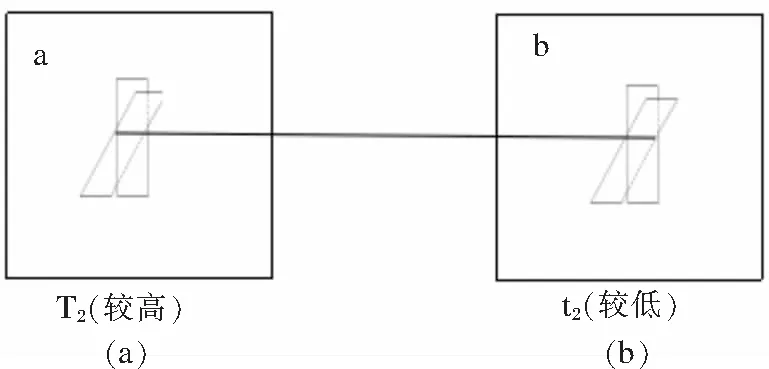
圖5 葉輪不單向轉動

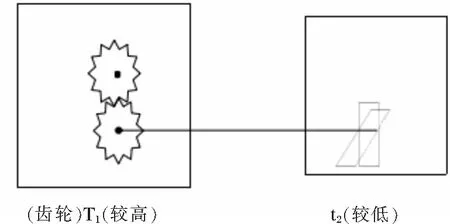
圖6 齒輪不單向轉動

我們知道卡諾循環是可逆過程，所以得到費曼棘輪也是可逆的。如文獻[2]所言，不應該混淆準靜態和可逆這兩個概念。事實上非平衡條件下的準靜態過程不可逆。這一點可以從下面的角度來分析：

圖5中，盡管葉輪和軸不直接傳熱，但兩箱中的氣體分子都在不停地和葉輪相互碰撞。由于T1較高，左箱中氣體分子振動得更劇烈，故它撞擊葉輪a更劇烈，對于理想葉輪，則在葉輪a的帶動下，葉輪b也振動得同樣劇烈，它就會主動撞擊比它溫度更低的右箱氣體分子，將能量傳給b箱。所以可以說葉輪a占主動，通過理想桿向葉輪b周圍的氣體分子輸出功，后者吸收功后熱運動更加劇烈，溫度升高，同時a箱中的氣體溫度在降低。顯然，只要時間足夠長，兩箱氣體的溫度將趨于一致。整個過程實際上正是一個由非平衡態自發回到平衡態的過程。與a、b中的氣體通過熱傳遞達到同一溫度并沒有本質的區別。由此可見，熱傳遞的微觀本質就是微觀運動，也是一種廣義的做功，只不過所做的功可以稱為“無序功”，直接由系統自身耗散掉了，不能被直接有效利用為人類服務。

同樣，圖6中齒輪也不會單向轉動。對比圖5、6與圖4c、圖7c，可得微觀棘輪單向轉動的另一個必要條件(外因)：存在適當的極性結構(如單側斜面)對非平衡作用進行“整流”。這是一種狹義的做功，所做的功為有序功，可以對外輸出，被直接有效利用為人類服務。同理，若我們將圖7a和b中的3、4點用理想桿連接，就成了圖7c。顯然，與圖4c一樣，圖7c中也是棘輪溫度T1，棘爪溫度t2，故棘輪也是正轉。

同樣，若將圖7a、c中的棘輪、棘爪互換，會怎樣？得到圖8。對比圖7c棘輪和圖8b棘輪會發現，圖8b中的棘輪應為反轉，因為棘爪溫度比棘輪高，能量是從棘爪傳到棘輪的，棘爪為主動，導致棘輪反轉。

3 深入分析及總結

換句話說，棘輪轉動和棘爪跳動在統計意義上是獨立無關的兩個事件，但在平衡態，二者無論溫度誰高誰低，高的一方將對低的一方做功(廣義的做功)。這種做功通常有兩種表現。直接表現：一方比另一方振動得更劇烈，沒有凈單向轉動(所做的是“無序功”)，棘輪不單向轉動。附加表現：在存在合適的極性結構(棘輪那樣的單側斜面)，后者對非平衡作用進行了 “整流”(所做的是“有序功”)棘輪單向轉動。表現結果是熱棘輪使自己正轉，熱棘爪使冷棘輪反轉。

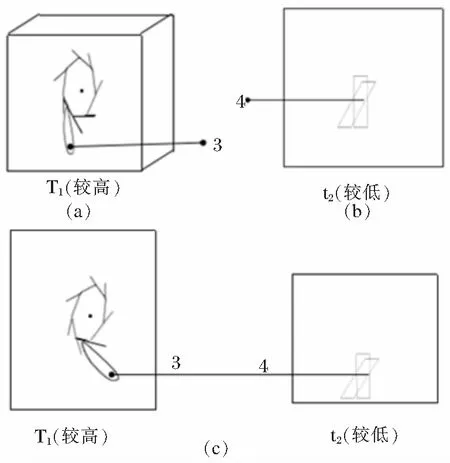
a 棘輪不單向轉; b 葉輪不單向轉； c 棘輪正轉

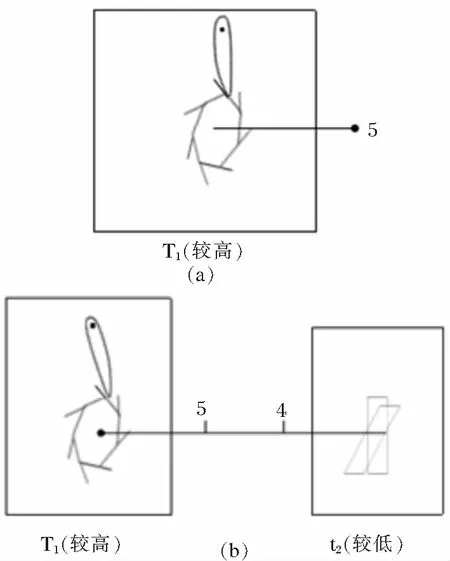
圖8 葉輪與棘輪連接、棘輪溫度高于葉輪溫度的費曼棘輪分析：棘輪正轉

4 結 論

微觀量子器件中的分子馬達是微觀機械系統與納米器件領域的重要器件，在微納機械電子器件系統中及量子生物物理領域有重要的應用前景。本文從宏觀棘輪的幾何特性出發分析了微觀棘輪在熱漲落下單向轉動的條件及其機理。結果得出了微觀棘輪單向轉動的兩大必要條件為：體系的非平衡性，即發生了不可逆過程(內因)；和存在適當的極性結構(如單側斜面)對非平衡作用進行“整流”，即環境的各向異性或軌道要提供穩定的極性(外因)。這些結論可以為相關的微觀量子器件中的納米器件的設計及應用提供有益的參考。

[1] Rechard F. 費曼物理學講義第一卷[M]. 上海：上海科學技術出版社，2013.

[2] Parrondo, Juan M R, Espaol Pep. Criticism of Feynman‘s analysis of the ratchet as an engine[J]. American Journal of Physics, 1996, 64(9): 1125-1130.

[3] 田莖.分子馬達定向運動機制的研究[D]. 鄭州：鄭州大學，2007.

[4] 施夏清，馬余強.活力物質的非平衡結構和動力學[J]. 物理，2012，41(1)：31-38.

[5] 文書堂.分子馬達定向運動物理機制研究[D]. 鄭州：鄭州大學，2004.

[6] 葛榮春.少體系統的量子關聯和量子棘輪[D]. 合肥：中國科學技術大學，2012.

[7] 馮玉宇.耦合布朗馬達的定向運輸研究[D]. 西安：西北農林科技大學，2015.

[8] 白文斯密，彭皓，屠浙.分數階Brown馬達及其定向輸運現象[J]. Acta. Phys. Sin.，2012，61(21)： 64-69.

[9] 程海濤.熱驅動布朗馬達的熱力學性能研究[D]. 南昌：南昌大學，2012.

[10] 陳磊.多光子干涉與量子棘輪效應[D]. 合肥：中國科學技術大學，2010.

[11] 陳良林.對稱周期勢場中粒子輸運的數值模擬研究[D]. 昆明：云南大學，2013.

[12] 王莉芳，高天附，黃仁忠. 外力作用下反饋耦合布朗棘輪的定向輸運[J]. Acta. Phys. Sin.，2013， 62(7)： 63-68.

[13] 程海濤，何濟洲，肖宇玲. 周期性雙勢壘鋸齒勢中溫差驅動的布朗熱機[J]. Acta. Phys. Sin.， 2012， 61(1)： 53-58.

StudyontheConditionMechanismofOne-wayRotationofMolecularMotorinMicroscopicQuantumDevices

SONG Yafeng1, ZHU Qinsheng2, JIAO Zhuangzhuang1, KONG Xiongxiong1, LI Huijie2

(1.DepartmentofPhysics,CollegeofElectronicInformationandElectricalEngineering,ShangluoUniversity,Shangzhou,Shanxi726000,China；2.KeyLaboratoryofSemiconductorMaterialsScience,InstituteofSemiconductors,ChineseAcademyofSciences,Beijing100083,China)

The molecular motor in microscopic quantum device is an important device in the field of micro-mechanical system and nanometer device. In this paper, the conditions and mechanism of one-way rotation are studied systematically. This paper analyzes the physical essence of macro ratchet work from the perspective of geometry. It obtains three necessary conditions. Two necessary conditions for one-way rotation of the microscopic ratchet read as follows: the non-equilibrium (internal) of the system and the proper polarity structure (external factor). These conclusions can provide a useful reference for the design and application of nanometer devices in related micro quantum devices.

Molecular motor; Ratcheting wheel; Heat fluctuation; Second law of thermodynamics

2017-07-13

國家自然科學基金項目(Nos.61504128，61504129，61274041，11275228)；陜西省自然科學基礎研究計劃資助項目(2017JQ6011)；商洛市科技局科研計劃資助項目(SK2015-35)；商洛學院科學與技術研究基金項目(15SKY025)。

宋亞峰(1984-)，男，山西介休人，博士，講師，研究方向：半導體低維結構與器件研究，電話：0914-2986020，E-mail：cumtsyf03@163.com.

TN389;TH136

A

10.14101/j.cnki.issn.1002-4336.2017.05.032