基于GNSS的晶振馴服方法分析

薛毅聰,龔航,劉增軍,朱祥維

(國防科技大學 電子科學與工程學院 衛星導航定位技術工程研究中心,湖南 長沙 410073)

基于GNSS的晶振馴服方法分析

薛毅聰,龔航,劉增軍,朱祥維

(國防科技大學 電子科學與工程學院 衛星導航定位技術工程研究中心,湖南 長沙 410073)

高穩定度、高準確度的頻標在計量測試、測控通信、電信電力、金融等領域至關重要。GNSS馴服晶振結合了GNSS具有較高長期穩定度和晶振具有較高短期穩定度的優點,加之成本較低,獲得了廣泛應用。本文針對GNSS馴服晶振的特點,對比分析了最小二乘法、無偏滑動平均濾波法、Kalman濾波法等幾種主要的晶振馴服濾波方法,并利用相同控制方法進行馴服仿真比對,給出了幾種濾波方法的馴服性能差異,分析了其優缺點。本文可以為馴服晶振在GNSS授時接收機的應用提供技術借鑒。

GNSS;晶振馴服;最小二乘;Kalman濾波

0 引 言

在導航定位、計量測試、測控通信、電信電力、金融等領域中,許多設備都需高精度的時間頻率基準進行協調同步工作,并且隨著導航、測量技術的發展,要求頻率標準精度越來越高[1]。在一般情況下,可以利用高穩定的恒溫晶體振蕩器來實現,準確度可達到10-9量級,在要求精度更高的場合可以選用銣鐘作為頻率標準,其準確度可達10-11量級[2]。但是采用晶體振蕩器或者銣鐘作為頻率標準的時統設備都存在一個問題:長期頻率漂移造成頻率準確度降低。然而更高一級的頻率標準(氫鐘,銫鐘)成本高,設備體積大,不能滿足普遍使用需求。所以提供一個高精度、低成本、滿足普遍使用需求的頻率標準源非常關鍵。

GNSS具有高精度的頻率基準(達到10-12～10-15),用戶可以通過GNSS授時接收機提取衛星系統的同步時鐘頻率,但是GNSS信號受大氣傳輸、相對論效應等因素影響[3],接收機在接收解調的過程中會引入各種噪聲,導致恢復出來的時鐘頻率雖然能夠跟蹤衛星信號的長期穩定度,但是也增加了短期的相位抖動,短期穩定度指標差。然而晶體振蕩器如OCXO、VCXO等具有短期穩定度好的優點,但存在老化的固有缺陷,長期穩定度差。在此基礎上發展出來的基于GNSS的晶振馴服技術能有效的結合上述的兩種優點,實現高穩定度的頻率輸出。

本文分析了基于GNSS的晶振馴服技術基本工作原理,針對GNSS馴服晶振的誤差模型特點,對比分析了最小二乘法、無偏滑動平均濾波法、卡爾曼濾波法等目前幾種主要的濾波方法,并利用常用的控制算法,進行晶振馴服仿真驗證,從而給出了幾種方法的優缺點以及適用條件。

1 基于GNSS的晶振馴服技術原理

對于GNSS晶振馴服技術的基本工作原理如圖1所示,利用GNSS授時接收機解算的鐘差,進行濾波處理計算出頻率偏移量后,利用相應的控制算法計算出加到晶振上的壓控電壓所對應的數字量,并通過高分辨率的D/A轉換器輸出該控制電壓,達到校正晶體振蕩器輸出頻率的目的[4],使晶振的振蕩頻率鎖定在GNSS時鐘上,從而提高晶振的長期穩定性。最終目的是實現GNSS衛星授時長期穩定性高和本地晶振短期穩定度高的優勢互補。

圖 1 基于GNSS的晶振馴服基本原理框圖

由上述原理可知,GNSS馴服晶振的主要環節是鐘差濾波算法和頻率控制方法,以下分別展開討論。

2 幾種常用濾波方法分析

在GNSS晶振馴服系統中,誤差來源受各項因素的影響,一方面系統精度與GNSS授時接收機輸出的鐘差有密切聯系,然而GNSS授時接收機解算的鐘差由于受衛星星歷誤差、電離層、對流層等因素影響存在誤差;另一方面根據晶振自身的誤差模型特點,晶振的頻率偏差、老化和溫度變化引起的頻率漂移率等也會造成影響。

根據晶振誤差模型,將其按照泰勒級數展開,并考慮晶振自身的特點,取泰勒級數的前三項,就滿足基于GNSS晶振馴服的要求[5].模型表達式為

xn=x0+x1τn+τ2n2x2/2+v(n),

(1)

式中:n的取值為1,2,3,…;τ為時間間隔;x0為初始頻率誤差;x1為晶振初始頻率偏差;x2為老化和溫度變化引起的線性頻率漂移率。

υ(n)是由GNSS接收機鐘差解算引起的誤差,包含多種誤差成分,如: 1) 衛星時鐘誤差; 2) 星歷誤差; 3)電離層的附加延時誤差; 4) 對流層的附加延時誤差; 5)多路徑誤差; 6)接收機本身的誤差等。而上述的誤差可以采用相應的模型或者其他鐘差修正方法進行修正處理,本文主要考慮修正后殘留誤差引起的噪聲。目前主要的鐘差濾波方法有最小二乘法、無偏滑動平均濾波法、卡爾曼濾波法等,以下分別進行分析討論。

2.1最小二乘法

最小二乘法是通過最小化誤差的平方尋找數據的最佳函數匹配。基于GNSS的晶振馴服誤差模型式(1),記錄n秒脈沖時鐘,計數器測得的值分別為Y1,Y2,Y3…Yn,這些測量值與初始頻率誤差x0、晶振初始頻率偏差x1、老化和溫度變化引起的線性頻率漂移率x2的聯系可由下式表示[6]:

(2)

根據上述矩陣求解可得晶振引入的初始頻率、晶振初始頻率偏差、老化和溫度變化引起的線性頻率漂移率這三個誤差參數。在存在隨機噪聲的情況下,最小二乘法利用求得的數據與實際數據之間誤差的平方和為最小的準則擬合計算使得給定測量的數據點的基本趨勢無限“逼近”真實值,擬合時間越長,求得的誤差值越接近真實值。

2.2無偏滑動平均濾波法

文獻[5]提出了一種無偏滑動平均濾波方法,是在普通滑動濾波[7]基礎上進行的改進,根據基于GNSS的晶振馴服誤差模型式(1),為了濾除GNSS接收機鐘差解算殘留修正誤差υ(n),首先采用普通滑動濾波方法對鐘差進行濾波,考慮到晶振誤差模型頻差存在,濾波時采用了滑動加權的方法,濾波表達式為

(3)

式中:N為滑動窗口窗長;Wi(n)為濾波器的第i個測量值的權值系數。由于晶振誤差模型中存在一、二次項,采用普通滑動濾波得到tn時刻的xn估計值存在偏差。為了補償估計偏差,在濾波之后采用線性最小二乘法估計xn,其表達式為

(4)

最小二乘估計采用的是方差最小準則,可用x(tn)代替tn時刻頻差真實值xn計算普通滑動濾波的偏差。整理代入計算得到Wi(N)的表達式:

(5)

由上式可知Wi(n)是i的單調遞減函數,i=0時,得到最大值2(2N-1)/(N2+N),i=N取得最小值-2(N+1)/(N2+N),說明離xn越近的測量誤差值對估計xn貢獻越大,這與實際情況相符[5]。

由上述可知，無偏滑動平均濾波法實際是利用線性回歸對普通算術滑動平均濾波器進行了改進,濾除了GNSS接收機鐘差解算殘留修正誤差υ(n)、晶振的頻偏、頻率漂移。改進后的平均滑動濾波器權值表達式簡單,窗長N確定可以根據系統的需求確定,當窗口值較大時,信號平滑度較高,靈敏度較低;當窗口值較小時, 信號平滑度較低,但靈敏度較高。

2.3卡爾曼濾波法

卡爾曼濾波是一種基于最小均方誤差準則的最優線性時域濾波器,是一種高效率的自回歸濾波器,能夠在包含噪聲的信號中估計動態系統的狀態。假設在n時刻解算得到的鐘差為X(n),則系統狀態方程為

X(n)=AX(n-1)+BU(n)+W(n),

(6)

觀測方程為

Z(n)=HX(n)+V(n),

(7)

其中:n為時間系數;A和B為系統狀態轉移矩陣,反映了系統從n-1時刻的狀態到n時刻狀態的變換關系;U為系統的已知輸入;W為過程噪聲向量;H為線性連接矩陣;V為觀測噪聲[2]。

在基于GNSS的晶振馴服系統中,鐘差上報的時間間隔為1s,X(n)為N時間差的真值,因此X(n)是一組三維向量,主要包括鐘差、頻差、頻漂的數據;Zn為包含觀測誤差的測量值,也是一組三維向量。由于系統對于GNSS接收機鐘差信號沒有控制量,因而可得U(n)為0.在實際的接收信號的過程中,信號是平穩一致的,因而系統參數A為1,觀測矩陣H(n)為1,對于觀測噪聲R的取值,依據經驗必須為1,否則鐘差值會在濾波后整體地變大或變小。對于過程噪聲方差矩陣Q為三階方陣,其對角線上的元素對應狀態向量中各項的過程噪聲方差,而其余項分別是狀態向量中各項之間的協方差,各項具體數據由試驗確定。簡化后的濾波器運算復雜度大大降低,迭代公式為

X(n)=X(n-1)+W(n),

Z(n)=X(n)+V(n),

P(n|n-1)=P(n-1|n-1)+Q,

X(n|n)=X(n|n-1)+

Kg(n)[Z(n)-X(n|n-1)],

P(n|n-1)=[1-Kg(n)]P(n|n-1).

(8)

基于GNSS的晶振馴服基本原理與卡爾曼濾波的“預測-實測-修正”反復遞推迭代的算法相符合,適合在晶振馴服系統中運用。在晶振馴服過程中,卡爾曼濾波能有效解決最佳線性濾波和估計的問題,對GNSS授時接收機鐘差解算殘留誤差有明顯的效果,經過多次測量和反復控制后,最終使得晶振輸出同步于GNSS授時接收機,從而實現對晶振的馴服和調整。與此同時采用該算法在晶振守時方面有比較明顯的優勢,即在GNSS接收機由于其他外部原因中斷鐘差數據時,該系統能根據觀測數據來預測下一次的測量值,使得晶振馴服系統具有較好的守時能力。

3 馴服控制方法

目前常用的控制算法有很多,比如PID控制、Fuzzy模糊控制、Optimal優化控制、Robust控制算法等等,在GNSS的晶振馴服系統中,控制量比較簡單,并且系統為閉環的反饋調節系統,采用典型的PID閉環控制方法較為合適。PID控制方法是一種線性控制系統,圖2示出了一個對輸入誤差e(n)進行控制的基本的PID控制系統結構。

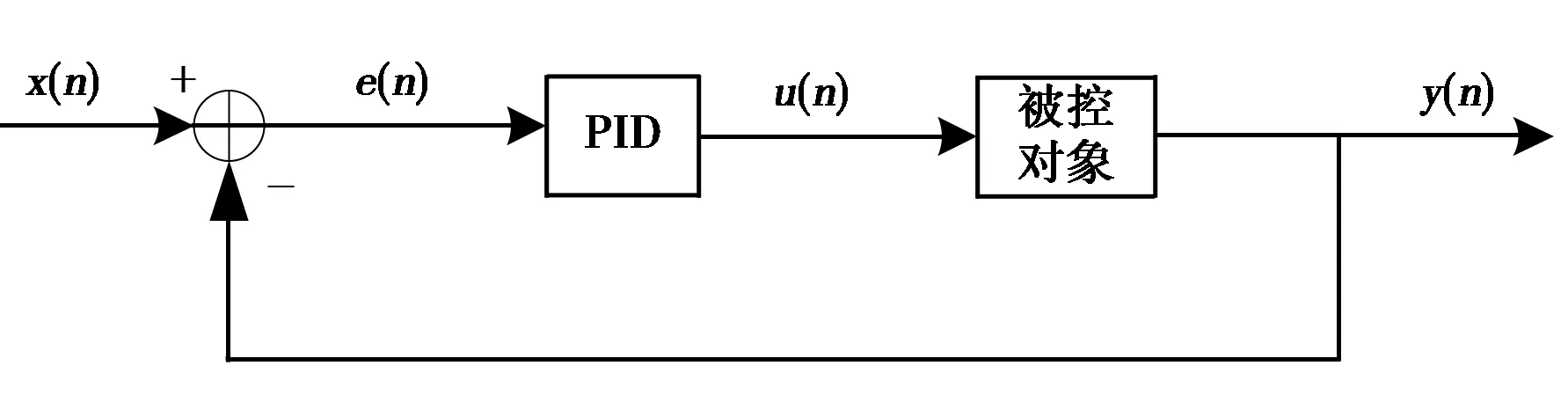
圖2 PID控制基本結構

圖中：x(n)為系統輸入；y(n)為當前輸出； 輸入與輸出的偏差為e(n)。在控制方法方面統一采用比例調節器進行仿真,控制簡單、快速,其輸出和輸入的誤差成比例關系,它用于調節偏差值,并在調節后將偏差控制在一定的固定值上,比例調節器的表達式為

u=KCe+u0，

(9)

式中:KC為比例系數;u0為控制量的基準,即e=0時的控制量。其中KC越大,控制作用越強,調節幅度也越大,KC越小控制作用越弱,調節幅度也越小[8]。

4 仿真實驗與方法比較

根據晶振的誤差模型分別對上述三種方法進行仿真。仿真條件為:初始頻率誤差x0=0,晶振初始頻率偏差x1=1×10-5,老化線性頻率漂移率x2=1×10-10,GNSS授時接收機鐘差解算殘留修正誤差υ(n)用均值為零、標準差為40 ns的白噪聲,采樣間隔為1 s,其中無偏滑動平均濾波的窗口N取值為100.馴服實驗結果如圖3、圖4所示。

圖3 晶振馴服結果比較

圖4 三種方法馴服結果比較

三種方法對晶振輸出的短期穩定度、長期穩定度[2,5-6]、24 h相位漂移等指標進行了對比,結果如表1所示。

表 1 三種方法的指標比較

根據上述方法比較及實驗結果,可以得出以下結論:

1) 三種方法均能實現晶振的馴服,馴服后系統的短期穩定度指標相對于晶振指標沒有明顯惡化,在長期穩定度指標方面得到明顯提升,提高三個量級;

2) 在實時馴服方面,最小二乘法基于平方和最小的準則,需要一段時間的數據采集擬合才比較準確,無法進行實時馴服;無偏滑動平均濾波隨窗口的向前滑動可隨窗口的滑動進行實時馴服;卡爾曼濾波利用“預測-實測-修正”反復遞推迭代方式,在實時馴服方面最具優勢;

3) 在馴服時間方面,卡爾曼濾波能使數據快速收斂,馴服時間最短;無偏滑動平均濾波則需等一個窗口值測量完畢才能進行馴服;最小二乘法實現馴服時間最長;

4) 在守時能力方面,卡爾曼濾波算法能對下一步測量進行預測守時能力最好,而最小二乘法,無偏平均滑動濾波兩種方法只能根據信號中斷前得測量值進行守時,效果不明顯。

5 結束語

本文分析了基于GNSS的晶振馴服技術工作原理,對比分析了最小二乘法、無偏滑動平均濾波法、卡爾曼濾波法三種主要的晶振馴服方法,并對這些方法進行了仿真實驗,在實際運用方面進行了比較,給出了幾種方法的優缺點,目前卡爾曼濾波法由于其在濾除噪聲、守時方面具有優勢運用較為廣泛。本文可以為馴服晶振在GNSS授時接收機的應用提供一定的技術借鑒。

[1] 賀洪兵. 基于GPS 的高精度時間同步系統的研究設計[D]. 成都: 四川大學, 2005.

[2] 孫江濤.基于GPS的1PPS的二級頻標馴服技術[D].西安：西安電子科技大學,2010.

[3] 向為,徐博,牟衛華, 等. 基于鎖相環的GNSS授時接收機鐘差校準算法[J].國防科技大學學報, 2013, 35(2): 115-119.

[4] 馬煦,孔維,孫海燕.基于GPS馴服時鐘的頻率校準系統的設計[J].電訊技術,2011,51(10):109-112.

[5] 張杰,周棟明. GPS馴服中無偏滑動平均濾波算法的研究[J].電子學報,2013,41(2):412-416

[6] 樊多盛,施韶華,李孝輝. 基于GPS 接收機的銣原子鐘駕馭方法研究[J], 電子測量與儀器學報,2013,27(10):980-984.

[7] 崔保健,王玉珍. GPS 馴服銣鐘頻標數據處理方法研究[J]. 電子測量與儀器學報,2010,24 (9):808-813.

[8] 范文晶. 基于 GPS 信號鎖定二級頻標技術的研究與實現[D]. 西安:西安電子科技大學, 2010.

AnalysisofDisciplinedCrystalOscillatorMethodBasedonGNSS

XUEYicong,GONGHang,LIUZengjun,ZHUXiangwei

(SatelliteNavigationR&DCenter,NationalUniv.ofDefenseTechnology,Changsha410073,China)

Contrast to the huge demand in measurement and testing, monitoring and communication, telecommunications and electricity and finance, a standard frequency source of high stability and high precision is crucial. GNSS disciplined crystal oscillator has combined the advantages of GNSS pulse per second signal which has good long-term stability and OCXO (Oven controlled crystal oscillators)which has good short-term stability. So GNSS disciplined crystal oscillator is widely applied for its high precision and low cost. In this paper, least squares algorithm, unbiased moving average filtering and Kalman filtering have been analyzed and compared.Those main filtering methods was applied to crystal oscillators which controlled in the same way.Their advantages and shortcomings have also been summed in this paper. Some meaningful suggestions are provided for the use of disciplined crystal oscillator in GNSS timing receiver.

GNSS; disciplined crystals oscillator; Least Square; Kalman filtering

10.13442/j.gnss.1008-9268.2017.04.007

P228.4

A

1008-9268(2017)04-0038-05

2017-03-10

聯系人: 薛毅聰 E-mail: xueyicong123@163.com

薛毅聰(1986-)，男，碩士研究生，主要從事GNSS時頻基準生成與測量技術研究。

龔航(1984-)，男，博士，講師，主要從事GNSS時間同步與時間頻率系統技術研究。

劉增軍(1982-)，男，博士，講師，主要從事衛星導航系統研究。

朱祥維(1980-)，男，博士，碩士生導師，副研究員，主要從事衛星導航系統研究。