32位定點運算數學庫IQmath在航空發動機FADEC系統中的應用

席偉俤，李偉剛，李鵬杰

（中國航發控制系統研究所，江蘇無錫 214063）

32位定點運算數學庫IQmath在航空發動機FADEC系統中的應用

席偉俤，李偉剛，李鵬杰

（中國航發控制系統研究所，江蘇無錫 214063）

為提高航空發動機FA D EC系統定點CPU的計算效率和計算精度，針對實際工程應用中的數學運算的方法展開討論，分析了定點數運算和浮點數運算在計算精度和運行效率方面存在的差異。參考TI公司的設計理念，自行設計了支持統一定點算法和可變定點算法的32位定點運算數學庫IQ math。在國內發動機控制領域不再依賴國外的庫函數，掌握了32位定點數學庫的源代碼，并在實際項目中應用了IQ math數學庫。試驗結果表明：IQ math數學庫的應用提高了定點CPU數學運算的精度和效率，完滿實現了預定的控制算法。

定點運算數學庫；全權限數字電子控制；定點數；浮點數；航空發動機

0 引言

隨著航空發動機技術和計算機技術的快速發展，發動機控制系統由早期的機械液壓式控制系統發展到現在的全權限數字電子控制(FADEC)系統，一方面使航空發動機性能有了很大提高，另一方面也對發動機控制系統的可靠性提出了更高要求。對控制系統的實時性和精確性有很高要求。對于定點CPU，國外已經掌握了定點數學運算庫的源代碼，而在國內普遍使用的是運算庫的動態連接庫，對于源代碼不可見，運算機理模糊。

在某型發動機FADEC系統中，數字電子控制器使用的CPU芯片不支持浮點運算，而實際應用的數據為浮點數，所以要將浮點數轉化為定點數之后才能運算，這就涉及到數的定標問題。本文針對FADEC系統嵌入式軟件定點CPU，自行設計了1種32位定點數學庫IQmath，掌握了定點運算庫的源代碼及運算機理。在實際項目應用中不但提高了定點CPU的運算效率，又保證了較高運算精度[1-6]。

1 定點數概述

定點數是計算機采用的1種數的表示方法，參與運算的數的小數點位置固定不變[7]，計算機僅僅考慮位。在整數運算中，位的位置表示2到2的高次冪(從右邊開始)。

因此 0000000000010000 表示數字 16（24），如圖1所示。從定點數的起點可以觀察到，有個隱含的十進制點(稱為基點)位于最右邊位值的右邊。

對于同樣的16位數，程序員決定將基點放在第5位和第 6位之間，使最右邊位表示 2～5。0000000000010000現在就不再表示16，而是0.5，如圖2所示。

通過改變基點的位置，程序員可以按比例縮小整數到1個小數值。基點的位置規定了程序如何解釋1個16位串。當基點向左移動時，小數變得更加精確，并且數字的全部范圍將縮小[8]。

為了利用定點運算，需要知道變量的取值范圍。定點運算操作通常執行時是快速的，因為大部分微處理器在執行整數操作時性能非常好。性能是以精度和復雜性為代價的。為了提高精度，不得不使用更多的位。當使用小的數字時定點運算產生的誤差大，而利用大數字時將產生相當好的結果。對于大數字，提高精度是利用更多位的結果。當數的變化范圍小時，定點數工作得非常好[9]。

2 32位定點數學庫IQmath介紹

2.1 32位IQ定點數

32位IQ定點數，是指選用32位有符號數作為基礎，由程序員自行約定小數點位置的數據表示方法。小數點的位置不同，32位IQ定點數能表示的范圍不同，數據精度也不同。不同位置小數點的數據類型用IQn表示，其中n從0取到31[10]。IQ類型的表示范圍和數據精度見表1。

表1 IQ類型的范圍和精度

在實際應用中，可采用2種32位IQ定點數的表示方法。第1種方法是在應用中每個數據和公式都可以采用不同的定標方法，即采用IQn中的n隨數據不同而變化[11]。第2種方法是在應用中每個數據和公式選用統一的定標方法，即采用IQn中的n是固定不變的。固定的n一般被稱為GLOBAL_Q。在1個應用中需要考慮到數據的精度和范圍，高精度必然會使數據的范圍變小，因此系統設計者必須權衡精度和范圍，然后設置GLOBAL_Q的值[12]。

2.2 IQmath支持的庫函數

本文參考TI公司的理念，自行設計了32位定點運算數學庫IQmath[13]。

32位定點數學庫IQmath是高度優化和具有高精度的數學函數庫集合。IQmath庫里面包含的函數均采用IQ格式定點數作為輸入/輸出，允許程序設計人員在定點CPU上進行浮點算法設計，從而提高運算速度[14-15]。

IQmath定點數學庫支持常見的算術運算和數學運算，主要運算介紹如下。

2.2.1 格式轉換

IQ ftoIQ(float F)將單精度浮點數轉為IQ數據；

Float IQtof(IQ A)將IQn數據轉為單精度浮點數。

2.2.2 算術運算

IQ定點數的加減法等于整數直接加減；

IQ iqMpy(IQ A,IQ B)，乘法函數；

IQ iqDiv(IQ A,IQ B)，除法函數；

IQ iqMpy_Div(IQ A,IQ B)，先乘后除函數。

2.2.3 數學運算

IQ iqabs(IQ A)，絕對值函數

IQ iqSqrt(IQ A)，算術平方根函數。

2.2.4 三角函數運算

IQ iqSin(IQ A)，三角正弦函數；

IQ iqCos(IQ A)，三角余弦函數；

IQ iqTan(IQ A)，三角正切函數；

IQ arcsin(IQ A)，反正弦函數；

IQ arccos(IQ A)，反余弦函數；

IQ arctan(IQ A)，反正切函數。

3 應用案例

3.1 統一定點算法應用

某型發動機FADEC系統中數字電子控制器使用的定點處理器不支持浮點運算，在程序運行時無法實現小數的操作，所以在計算時必須先把小數轉化為整數。采用IQmath定點數學庫可以將浮點數算法轉換為定點數算法，使運算速度明顯提高，對強實時性要求的發動機控制系統的設計十分有效。

在某型發動機控軟件的開發中，需實現如下控制計算

式中：R為面積比；a為某系數；D8為喉道直徑，m；δ為偏轉角，（°）；θ為方位角，（°）；δH為調節環與作動筒平面偏轉角，（°）；LH為水平位移，mm；Z1、Z2、Z3為作動筒長度，mm；U為某修正系數；C為常數，mm。

該算法要求計算精度高，采用常見的16位定點算法很難滿足要求，而且整個定點化過程非常復雜，會降低軟件的可維護性。經過項目實際應用場景分析及結合圖3中IQ類型數據的范圍和精度考量，選用IQ-math定點數學庫統一定點方式進行算法設計。將GLOBAL_Q統一定義為19，其軟件計算流程如圖3所示。

IQ定點算法控制軟件配套某型數控系統進行了外場試車，試車數據如圖4所示。浮點理論計算數據與IQ定點計算試驗數據對比結果見表2。

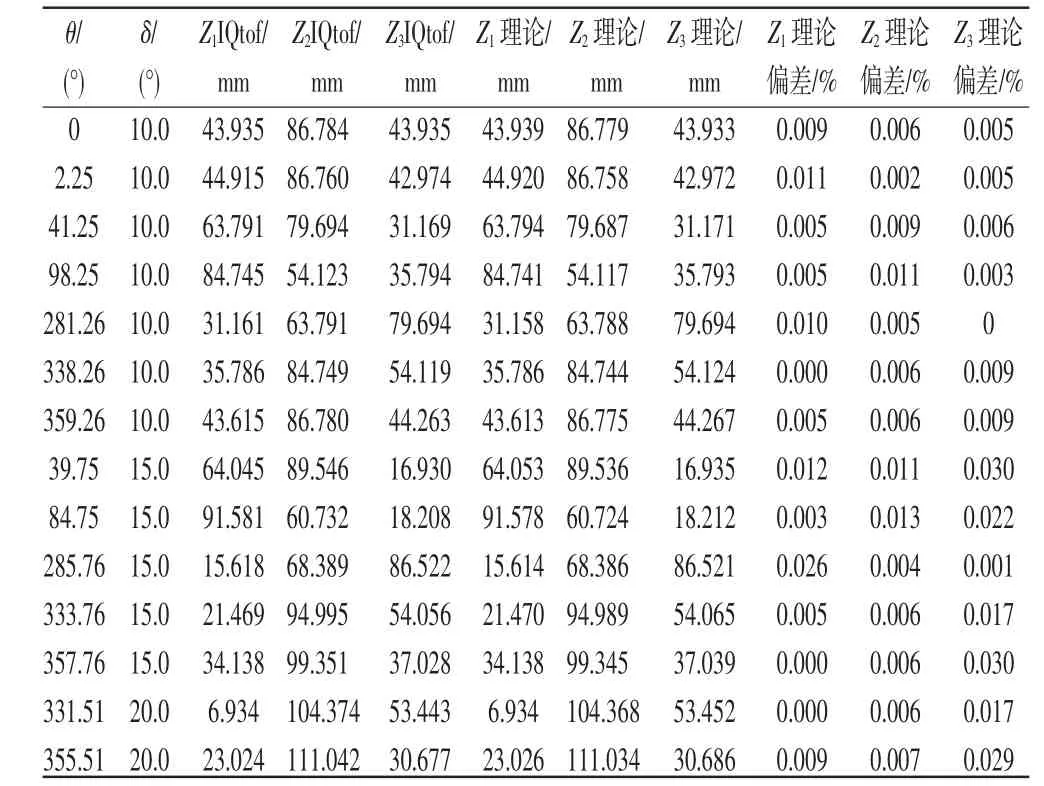
表2 IQ定點計算數據與浮點理論計算數據對比

表 2 中 Z1IQtof、Z2IQtof、Z3IQtof 是 θ、δ、D8（D8=0.584 m）等輸入變量按照GLOBAL_Q=19統一定點算法計算后的結果再經過反定點化為浮點數的結果，所有定點計算結果未超過IQ19類型數據表示的范圍[-4096,4095.999998093]）；Z1、Z2、Z3理論是同樣的輸入數據按照浮點數計算得出的結果。浮點數理論和統一定點算法的計算結果最大偏差為0.03%，完全滿足客戶的計算精度偏差在0.05%以內的要求。

3.2 可變定點算法應用

某型FADEC系統中對某信號有超前滯后校正要求

式中：b為超前校正系數，其取值根據傳感器時間常數確定，用于修正傳感器采集的延遲；a為滯后校正系數，由發動機特性決定。

對于上述信號超前滯后校正算法采用IQmath定點數學庫GLOBAL_Q=19統一定點算法，當輸入數據經過校正處理后超過4095.999998093，計算結果出現溢出翻轉問題，數據見表3。表3中統一定點算法超前滯后校正結果由于出現計算溢出問題，導致與浮點理論超前滯后校正結果偏差較大，不滿足設計初衷，嚴重影響發動機控制效果和安全。

同樣的輸入數據及超前滯后校正系數，采用可變定點算法就解決了計算溢出問題。數據定標為IQn(n可變，暫取n=12；數據范圍為[-524288,524287.999755859]），輸入數據經過超前滯后校正處理后未出現超過IQ12類型數據范圍的問題，數據見表4。表4中浮點理論超前滯后校正結果與可變定點算法超前滯后校正結果最大偏差為0.03797%，滿足工程應用中偏差在0.05%以內的要求。

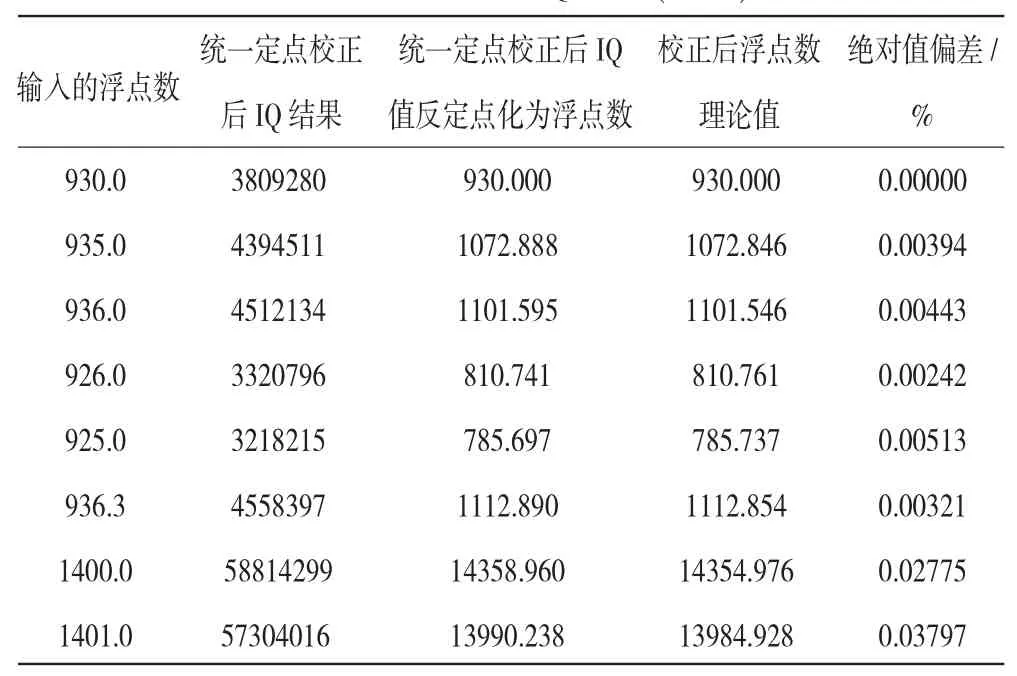
表4 可變定點IQ數據(n=12)

4 結束語

本文自行設計的32位定點運算數學庫IQmath，不僅在國內發動機控制領域掌握了32位定點數學庫的源代碼，不再依賴國外的庫函數，而且成功地應用于航空發動機FADEC系統嵌入式控制軟件中。此外IQmath數學庫的統一定點算法和可變定點算法選擇靈活，具有極高的工程應用價值，可推廣應用到其他行業控制領域中。

[1]段彬，孫同景，李振華，等.快速浮、定點PID控制器FPGA的研究與實現[J].計算機工程與應用，2009，45（36）：202-206.DUAN Bin，SUN Tongjing，LI Zhenhua，et al.Research and application on fast floating and fixed point PID controllers on FPGA[J].Computer Engineering and Applications，2009，45（36）：202-206.（in Chinese）

[2]范嘯濤，季光明，何永斌.計算機浮點數算術運算的舍入誤差研究[J].成都理工大學學報(自然科學版)，2005，32（2）：213-216.FAN Xiaotao，JI Guangming,HE Yongbin.Rounding error study of calculator floating-point numbers arithmetic operation[J].Journal of Chengdu University of Technology (Science&Technology Edition)，2005，32（2）：213-216.（in Chinese）

[3]張宗杰，張明亮.C語言中浮點數的存儲格式及其有效數字位數[J].計算機與數字工程，2006，34（1）：84-86，90.ZHANG Zongjie，ZHANG Mingliang.Storage format of a binary floating-point number and its bits of decimal significant digits[J].Computer&Digital Engineering，2006，34（1）：84-86，90.（in Chinese）

[4]何克晶.科學計算浮點數據的高性能無損壓縮 [J].計算機學報，2010，33（6）：966-976.HE KeJing.High performance lossless compression of scientific floating data[J].Chinese Journal of Computers，2010，33 （6）：966-976.（in Chinese）

[5]Institute of Electrical and Electronics Engineers (IEEE).IEEE 754-1985:IEEE Standard for floating-point arithmetic[S].Microprocessor Standards Committee,1985.

[6]Institute of Electrical and Electronics Engineers (IEEE).IEEE 754-2008:IEEE Standard for floating-point arithmetic[S].Microprocessor Standards Committee,2008.

[7]邵正芬.最佳精度定點運算的FPGA實現 [J].通信技術，2009，42（7）：279-281.SHAO Zhengfen.FPGA implementation of best-precision fixed-point algorithm[J].Communications Technology，2009，42（7）：279-281.（in Chinese）

[8]Texas Instruments Incorporated.TMS320C28x Assembly language tools user’s guide[OL].[2006-03].http://www.docin.com/p-30611705.html

[9]徐彥凱，雙凱.提高定點精度的FPGA信號處理算法[J].計算機工程與科學，2012，34（9）：197-200.XU Yankai,SHUANG Kai.An algorithm of increasing fixed-point accuracy for signal processing systems with FPGA[J].Computer Engineer ing&Science，2012，34（9）：197-200.（in Chinese）

[10]Texas Instruments Incorporated.Module user’s guide C28x foundation software [OL]. [2008-01-07].http://www.doc88.com/p-241831 099821.html

[11]谷海濤，顏湘武，于世濤.新型電機控制芯片TMS320F2812[J].微電機，2005，38（2）:53-56.GU Haitao,YAN Xiangwu,YU Shitao.A new chip for motor control-TMS320F2812[J].Servo Technique，2005,38（2）:53-56.（in Chinese）

[12]張銳.TMS320F2812混合編程的研究與應用[J].煤炭技術，2008，27（1）：126-128.ZHANG Rui.Research and usage of TMS320F2812 mixed programming[J].Coal Technology，2008，27（1）：126-128.（in Chinese）

[13]彭志明，李琳.基于IQmath庫的定點DSP算法設計[J].新器件技術，2010（9）：39-41.PENG Zhiming,LI Lin.Fixed point DSP algorithm based on IQmath library[J].New Product&Technology,2010（9）：39-41.（in Chinese）

[14]魏光，裴郡，林宗宏，等.IQmath在雙體船航行控制器設計中的應用[J].武漢理工大學學報(信息與管理工程版)，2015，37（2）：47-51.WEI Guang，PEI Jun，LIN Zonghong，et al.Application of IQmath in design on navigation controller of catamaran[J].Journal of Wuhan(Information&Management Engineering)，2015，37（2）：47-51.（in Chinese）

[15]李翰麟，潘厚宏，王濤，等.IQmath在基于PWM實現的D/A轉換調試中的應用 [J].重慶工學院學報 (自然科學版)，2009，23（8）：139-143.LI Hanlin，PAN Houhong，WANG Tao，et al.Applications of IQmath in PWM-based D/A conversion debugging[J].Journal of Chongqing Institute of Technology(Natural Science)，2009，23 （8）：139-143.（in Chinese）

Application of 32 bit Fixed-point Arithmetic Library IQmath in FADEC System of Aeroengine

XI Wei-di LI Wei-gang LI Peng-jie
（AECC Aero Engine Control System Institute,Wuxi Jiangsu 214063， China）

In order to improve the computational efficiency and accuracy of the fixed-point CPU of Aeroengine FADEC system,the mathematical operation method in practical engineering application was discussed and the differences between the fixed-point operation and the floating-point operation in the calculation accuracy and the running efficiency were analyzed.Reference to TI's design concept,arithmetic library IQmath was designed,which support the unified fixed-point algorithm and variable fixed-point algorithm 32-bit fixedpoint.In the field of domestic engine control is no longer dependent on foreign library functions,the 32-bit fixed-point mathematical library of the source code was mastered,and the IQmath library was applicated in actual project.The results show that the application of IQmath library improves the accuracy and efficiency of fixed-point CPU mathematical operation,and realizes the predetermined control algorithm.

IQmath;FADEC;fixed-point numbers;floating-point numbers;aeroengine

V 233.7

A

10.13477/j.cnki.aeroengine.2017.05.004

2017-03-11

席偉俤（1982），男，碩士，工程師，主要從事航空發動機數控系統控制軟件的研究與應用工作；E-mail：275392963@qq.com。

席偉俤，李偉剛，李鵬杰.32位定點運算數學庫IQmath在航空發動機FADEC系統中的應用[J].航空發動機，2017，43（5）：21-25.XI Weidi LI Weigang,LI Pengjie.Application of 32 bit fixed-point arithmetic library IQmath in FADEC system of Aeroengine[J].Aeroengine，2017，43（5）：21-25.

(編輯：李華文)