大范圍網絡RTK基準站間整周模糊度實時快速解算

王建敏，李亞博，馬天明，祝會忠

(遼寧工程技術大學測繪與地理科學學院，遼寧 阜新 123000)

大范圍網絡RTK基準站間整周模糊度實時快速解算

王建敏，李亞博，馬天明，祝會忠

(遼寧工程技術大學測繪與地理科學學院，遼寧 阜新 123000)

網絡RTK是目前實現高精度實時動態定位的重要手段之一，而網絡RTK高精度定位的關鍵問題是基準站間整周模糊度的實時快速準確固定。對于大范圍網絡RTK，由于基準站間距離的增加，電離層延遲誤差、對流層延遲誤差和衛星軌道誤差相關性降低，導致基準站間整周模糊度不能快速準確地固定，因此本文提出了一種大范圍網絡RTK基準站間整周模糊度固定算法。該算法首先利用L1、L2載波相位觀測值和P1、P2偽距觀測值解算基準站間的雙差寬巷模糊度；然后采用Saastamoinen模型和Chao映射函數模型相結合解算雙差對流層延遲誤差，并將雙差寬巷模糊度作為L1、L2雙差載波相位整周模糊度的約束關系來確定L1、L2雙差載波相位整周模糊度；最后采用CORS站的實測數據進行試驗，并將本文的試驗結果同GAMIT軟件的解算結果進行比對，結果表明該算法可以快速準確地實現單歷元雙差載波相位整周模糊度的固定。

大范圍；網絡RTK；基準站；整周模糊度；對流層延遲

網絡RTK技術是目前實現高精度定位的重要手段之一，其關鍵問題是基準站間整周模糊度的準確解算，只有準確地確定了基準站間的整周模糊度，才能建立高精度的誤差模型，進而實現流動站整周模糊度的固定和得到高精度的定位結果。網絡RTK基準站間的距離一般達到50 km左右，電離層延遲和對流層延遲等誤差對雙差觀測值的影響遠遠大于0.5周，因此采用簡單的差分算法很難準確固定基準站間的整周模糊度[1]。目前，國內外學者對網絡RTK基準站間模糊度的解算進行了大量研究并取得了初步成果，文獻[1]和文獻[2]提出了中距離網絡RTK模糊度解算方法[2]；文獻[3]提出了模糊度的單歷元解算方法[3]，文獻[4]和文獻[5]提出對流層延遲的誤差解算模型，提高了模糊度浮點解的精度，但是目前已有的這些網絡RTK基準站間模糊度的解算方法站間距只能達到80 km；而大范圍的網絡RTK基準站間的距離達到150 km左右[2,4-5]，現有的網絡RTK基準站間模糊度的解算方法很難準確快速地固定模糊度，因此本文提出一種大范圍網絡RTK基準站間整周模糊度的解算方法，首先利用L1、L2載波相位觀測值和P1、P2偽距觀測值解算基準站間的雙差寬巷模糊度，然后與無電離層組合觀測方程聯立消除電離層延遲誤差，采用Saastamoinen模型和Chao映射函數模型相結合的方法解算雙差對流層延遲誤差，最終確定L1、L2雙差載波相位整周模糊度。

1 觀測方程

1.1 雙差觀測方程

載波相位雙差觀測方程不僅消除了接收機鐘差和衛星鐘差，而且大大削弱了電離層延遲誤差、對流層延遲誤差、衛星軌道誤差等誤差的影響[6]，因此本文采用雙差觀測值解算基準站載波相位整周模糊度。偽距和載波相位雙差觀測方程分別為

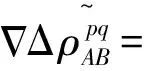
(1)

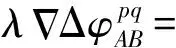
(2)

1.2 雙差觀測方程線性化

在雙差觀測方程中，基準站坐標被視為已知值，因此基準站方向余弦值為零[7]，因此雙差觀測方程線性化后的形式分別為

(3)

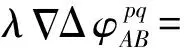
(4)

式中

(5)

(6)

(7)

2 基準站整周模糊度解算

2.1 雙差寬巷模糊度解算

在解算大范圍網絡RTK基準站間整周模糊度的過程中，隨著基準站間距離的增大，對流層延遲誤差、電離層延遲誤差和衛星軌道誤差殘差嚴重影響載波相位整周模糊度的固定，因此，本文采用不受電離層延遲誤差、對流層延遲誤差、衛星軌道誤差和幾何距離影響的MW組合觀測值解算雙差寬巷模糊度[8]，即

(8)

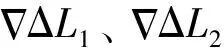
因為MW組合觀測值消除了電離層延遲誤差、對流層延遲誤差和衛星軌道誤差等誤差的影響，只受觀測噪聲的影響，所以可以通過多個歷元的平均值來求解雙差寬巷整周模糊度。為了保證解算出的雙差寬巷整周模糊度的正確性，需要對解算出的雙差寬巷整周模糊度進行驗證，以保證雙差寬巷整周模糊度的準確固定[9-10]。利用3個基準站組成的閉合基線雙差寬巷整周模糊度之和為零來驗證，即

(9)

2.2 誤差處理

在寬巷雙差整周模糊度準確固定后，為了保證載波相位整周模糊度的準確固定，需要對各項誤差進行處理。本文采用的是廣播星歷數據進行解算，對于200 km長度以下的基線而言，衛星軌道誤差可以忽略不計，電離層延遲誤差可以通過無電離層組合觀測值消除，而基準站一般設在比較開闊的地方，這在一定程度上削弱了多路徑效應的影響，除對流層延遲以外的其他誤差通過雙差觀測值處理以后的殘差可以忽略不計，因此只需要著重處理對流層延遲的誤差。

首先，采用Saastamoinen模型[11-13]計算天頂對流層的干、濕延遲分量，公式為

天頂干延遲分量

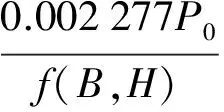
(10)

天頂濕延遲分量

(11)

式中，標準大氣壓P0=1 013.25 mbar；標準水汽壓e0=11.691 mbar；標準絕對溫度T0=288.15 K；f(B,H)是與基準站大地坐標相關的函數，可表示為

f(B,H)=1-0.002 66cos(2B)-0.000 28H

(12)

式中，(B,H)表示測站的大地坐標緯度和高程。選擇Chao映射函數模型[14-15]作為解算對流層延遲的映射函數，如式(13)所示。最后，根據式(14)解算雙差對流層延遲誤差。

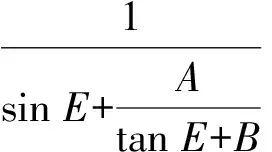
(13)

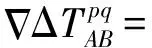
(14)

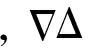
2.3 雙差載波相位模糊度解算

通過誤差處理后，基準站A、B對衛星p、q的載波相位雙差觀測方程可表示為

(15)

由式(15)可得到雙差無電離層組合載波相位觀測方程為

(16)

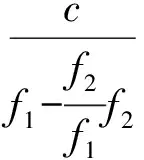
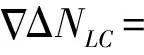
(17)

將式(17)代入式(16)雙差無電離層組合載波相位觀測方程可得

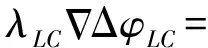
(18)

因此，利用式(18)即可實現L1載波相位雙差整周模糊度的解算，而L2載波相位雙差整周模糊度可以表示為

(19)

為了保證解算出的載波相位雙差整周模糊度的正確性，需要對解算出的載波相位雙差整周模糊度進行驗證，以保證解算出的載波相位雙差整周模糊度的可靠性。利用3個基準站組成的閉合基線載波相位雙差整周模糊度之和為零來驗證，即

(20)

如果解算出的L1、L2載波相位雙差整周模糊度滿足式(20)，則認為解算出的載波相位雙差整周模糊度是正確的。

3 試驗分析

為了驗證本文算法的正確性，采用CORS站的實測數據進行檢驗，采用2014年10月9日采集的CORS站數據進行大范圍網絡RTK基準站間模糊度的解算，衛星截止高度角設置為15°，數據采樣率為15 Hz。

首先利用本文提出的基準站間雙差寬巷整周模糊度的解算方法解算基準站間的雙差寬巷整周模糊度，同時將本文的解算結果與GAMIT軟件解算結果進行比較，這里以16號衛星為基準衛星，23號衛星的解算結果為例，GAMIT軟件的解算結果見表1，3條基線的雙差寬巷模糊度的解算結果如圖1—圖3所示。

表1 PRN23雙差寬巷整周模糊度正確解

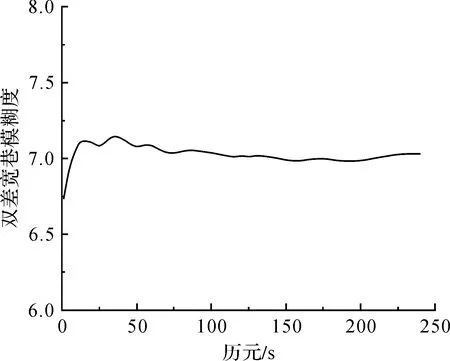
圖1 基線Base1—Base2雙差寬巷模糊度

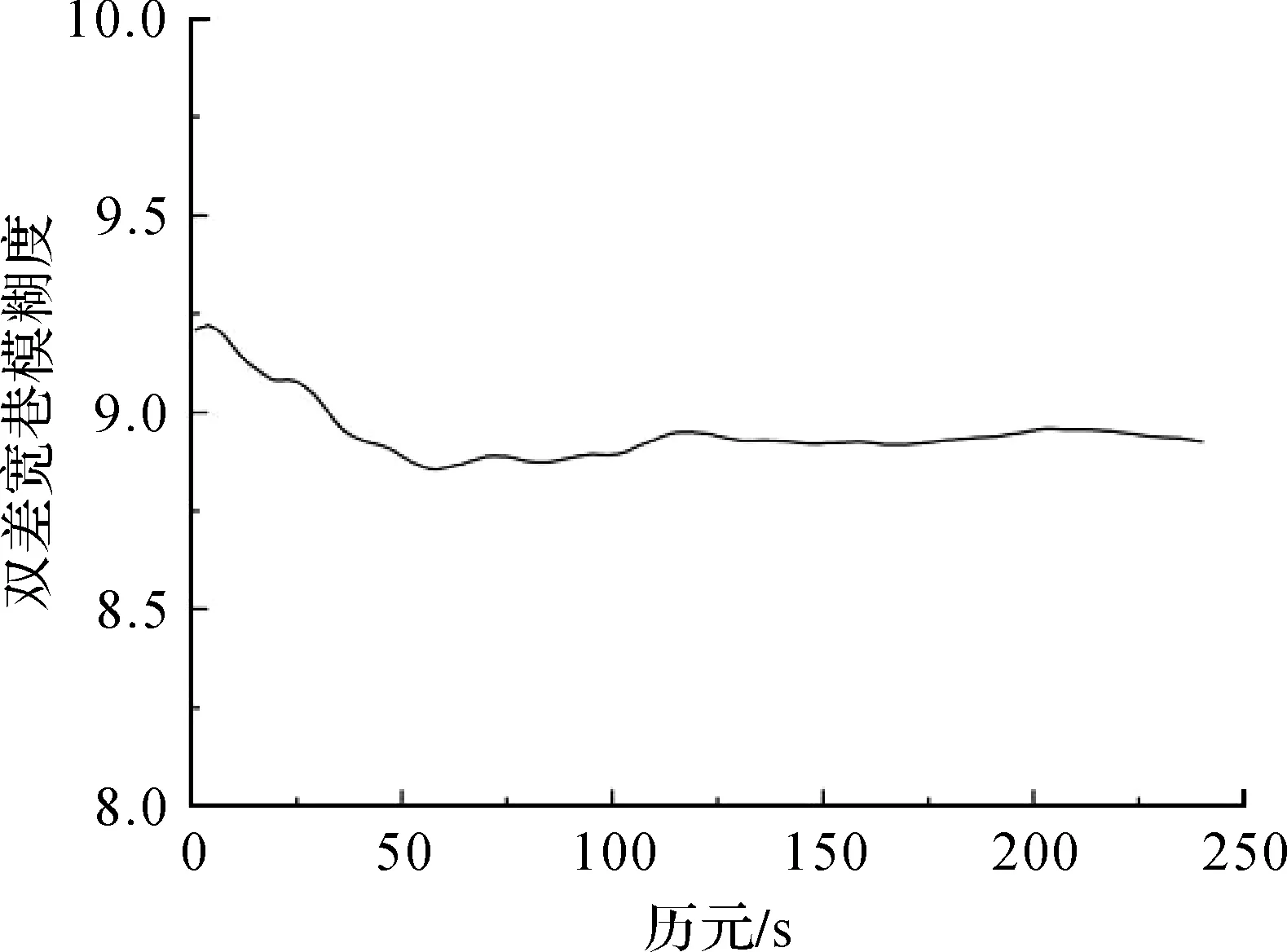
圖2 基線Base2—Base3雙差寬巷模糊度

圖3 基線Base3—Base1雙差寬巷模糊度

從圖1—圖3中可以看出，雙差寬巷模糊度的浮點解只需要大約2 min的時間即可收斂，然后趨于穩定，因為本文采用多個歷元求平均值的算法減少了觀測噪聲的影響，使雙差寬巷模糊度計算值越來越穩定，3條基線的雙差寬巷模糊度依次收斂于7、9和-16，與表1中GAMIT軟件的解算結果相同，同時滿足雙差寬巷模糊度的檢核條件(式(19))，證明該算法可以準確快速地解算大范圍網絡RTK基準站間雙差寬巷整周模糊度。

在正確解算出基準站間雙差整周模糊度以后，采用Saastamoinen模型和Chao映射函數模型相結合的方法解算雙差對流層延遲誤差，然后根據式(18)解算雙差載波相位整周模糊度，這里只給出L1雙差載波相位模糊度解算結果，L2載波結果與L1載波類似。結果如圖4—圖6所示，同時將本文的解算結果與表2中的GAMIT軟件的解算結果進行比較，這里仍以16號衛星為基準衛星，23號衛星的解算結果為例。

表2 PRN23雙差載波整周模糊度正確解

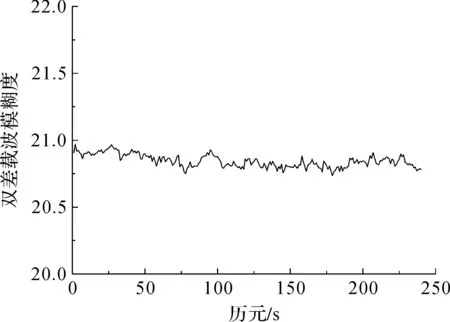
圖4 基線Base1—Base2雙差載波模糊度

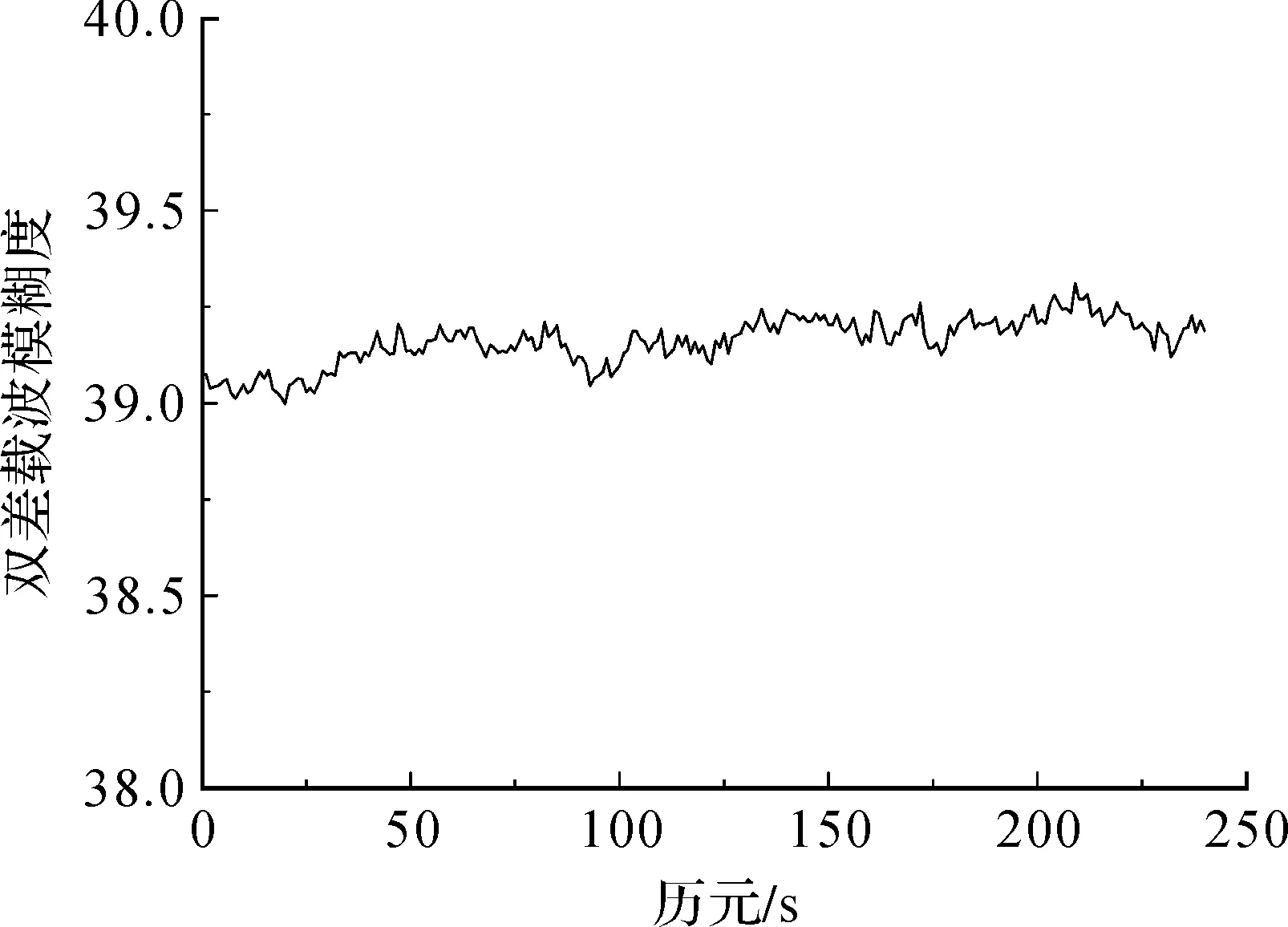
圖5 基線Base2—Base3雙差載波模糊度

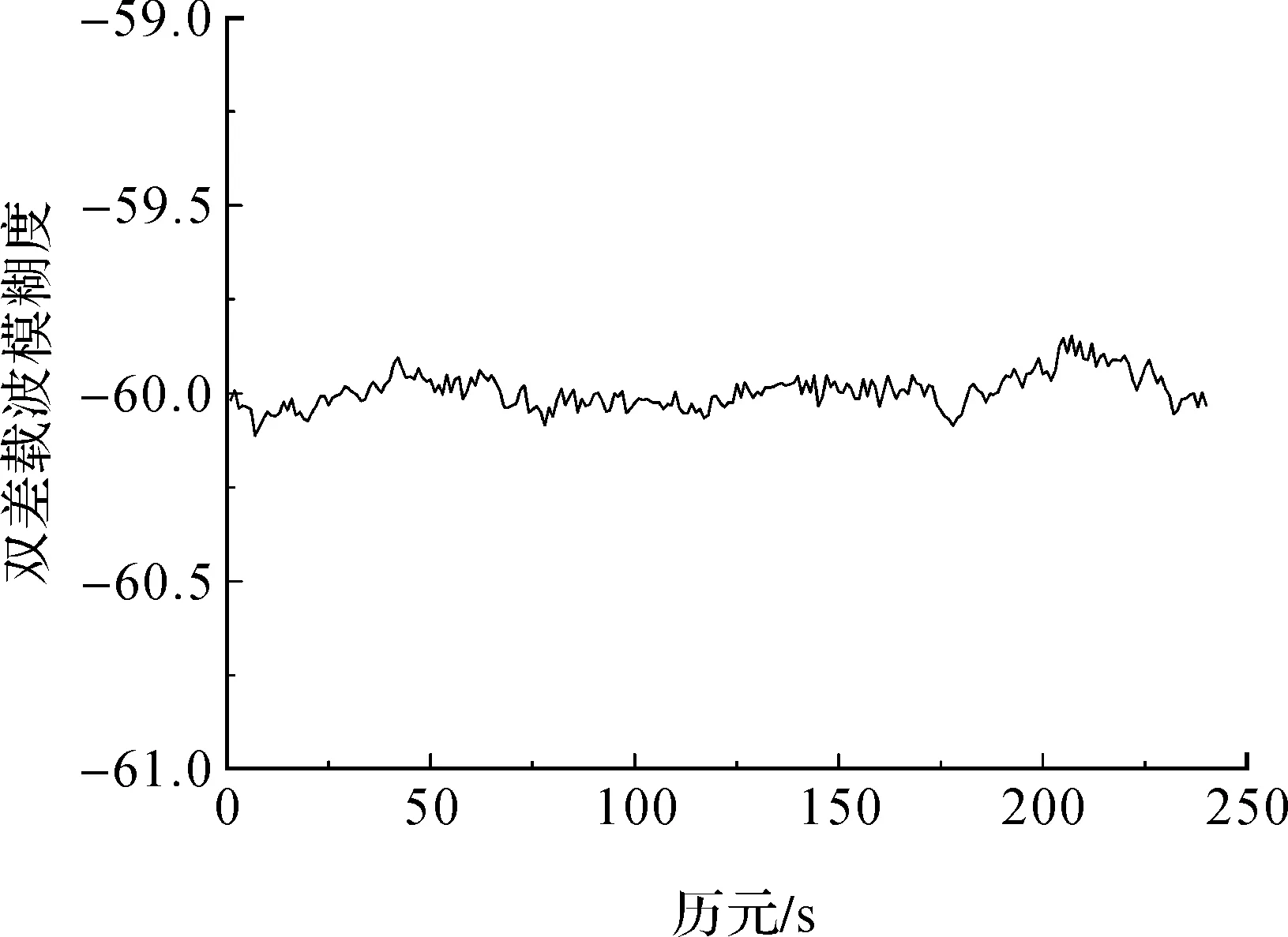
圖6 基線Base3—Base1雙差載波模糊度

從圖4—圖6中可以看出，雙差載波相位模糊度的浮點解單歷元即可收斂，3條基線的雙差載波相位模糊度依次收斂于21、39和-60，與表2中GAMIT軟件的解算結果相同，同時滿足雙差載波相位模糊度的檢核條件(式(20))，證明該算法可以準確快速地解算大范圍網絡RTK基準站間雙差載波相位整周模糊度。

4 結 語

本文首先采用L1、L2載波相位觀測值和P1、P2偽距觀測值組成的MW組合觀測值解算基準站間的雙差寬巷模糊度，然后與無電離層組合觀測方程聯立消除電離層延遲誤差，采用Saastamoinen模型和Chao映射函數模型相結合的方法解算雙差對流層延遲誤差，最終確定L1、L2雙差載波相位整周模糊度。經CORS網實測數據實驗算例的驗證，該方法可以實現大范圍網絡RTK基準站間的載波相位整周模糊度的實時快速準確解算，同時，用Saastamoinen模型和Chao映射函數模型相結合的方法解算雙差對流層延遲誤差在達到同樣精度的情況下模型簡便，計算量小，提高了載波相位整周模糊度的解算效率，實現了雙差載波相位整周模糊度的單歷元固定。

[1] 祝會忠,徐愛功,高猛,等.BDS網絡RTK中距離參考站整周模糊度單歷元解算方法[J].測繪學報,2016,45(1):50-57.

[2] 王珍.網絡RTK動態中長基線模糊度解算方法比較研究[J].測繪與空間地理信息,2016,39(2):71-74.

[3] 劉會,鄭衍寧,徐琪堯,等.一種GPS單歷元整周模糊度固定方法[J].導航定位學報,2016,4(2):57-61.

[4] 祝會忠,徐愛功,高猛,等.長距離網絡實時動態對流層延遲誤差改正[J].測繪科學,2015,40(6):30-35.

[5] 王建敏,黃佳鵬,祝會忠,等.電離層總電子數預報方法研究[J].測繪科學,2016,41(12):47-52.

[6] 呂偉才,高井祥,張書畢,等.寬巷約束的網絡RTK基準站間模糊度固定方法[J].中國礦業大學學報,2014,43(5):933-937.

[7] 李磊,徐愛功,祝會忠,等.長距離網絡RTK基準站間整周模糊度的快速解算[J].測繪科學,2014,39(10):22-25.

[8] 祝會忠,劉經南,唐衛明,等.長距離網絡RTK基準站間整周模糊度單歷元確定方法[J].測繪學報,2012，41(3):359-365.

[9] 柯福陽,王慶,潘樹國.網絡RTK長基線模糊度解算方法研究[J].大地測量與地球動力學,2012,32(5):72-77.

[10] 王建敏,馬天明,祝會忠.改進LAMBDA算法實現BDS雙頻整周模糊度快速解算[J].系統工程理論與實踐,2017,37(3):768-772.

[11] SAASTAMOINEN J.Contributions to Theory of Atmospheric Refraction[J].Journal of Geodesy,1972,105(1):279-298.

[12] SAASTAMOINEN J.Introduction to Practical Computation of Astronomical Refraction[J].Journal of Geodesy,1972,106(1):383-397.

[13] SAASTAMOINEN J.Contributions to the Theory of Atmospheric Refraction Part II:Refraction Corrections in Satellite Geodesy[J].Journal of Geodesy,1973,107(10):13-34.

[14] 趙鐵成,韓曜旭.GPS定位系統中幾種對流層模型的探討[J].全球定位系統,2011,36(1):46-52.

[15] 王鵬旭,呂志偉,楊東森,等.一種新的中長基線BDS三頻模糊度快速解算方法[J].測繪通報,2017(4):25-29.

[16] 王建敏,馬天明,祝會忠.BDS/GPS整周模糊度實時快速解算[J].中國礦業大學學報,2017,46(3):672-678.

[17] 謝建濤,郝金明,于合理,等.基于BDS+GPS中長基線多頻RTK定位的快速收斂模型[J].測繪通報,2016(5):6-10，17.

RealTimeandFastAlgorithmforIntegerAmbiguityofReferenceStationsinLarge-scaleNetworkRTK

WANG Jianmin,LI Yabo,MA Tianming,ZHU Huizhong
(School of Geomatics,Liaoning Technical University,Fuxin 123000,China)

Network RTK,at present,is one of the important means to realize high precision and real-time dynamic positioning,while the key problem of high precision positioning of network RTK is the real-time, fast and accurate fix of the integer ambiguity between reference stations.For a wide scale network RTK, because the distance between reference stations has increased and the ionospheric delay error、the troposphere delay error and satellite orbit error have a low correlation that leads to integer ambiguity in the reference stations can not solve quickly and accurately,therefore this paper presents a method that integer ambiguity algorithm in a wide scale network RTK reference stations.Firstly,this algorithm takes advantage of L1、L2 carrier phase observations and P1、P2 pseudorange observations to calculate the double difference wide lane ambiguity between reference stations,and then to solve double difference troposphere delay by combining Saastamoinen model with Chao mapping function model,at the same time,the thesis takes the double difference wide lane ambiguity regard as constraint condition of L1、L2 double difference the carrier phase integer ambiguity so as to make sure L1、L2 double difference carrier phase integer ambiguity.The experiment was carried out by using the measured data of CORS,at the same time,the experimental results of this paper are compared with the results of GAMIT software show that the algorithm can achieve single epoch double difference carrier phase fixed integer ambiguity stably and accurately.

large scale；network RTK；reference station；integer ambiguity；tropospheric delay

王建敏，李亞博，馬天明，等.大范圍網絡RTK基準站間整周模糊度實時快速解算[J].測繪通報，2017(10)：7-11.

10.13474/j.cnki.11-2246.2017.0307.

2017-02-23

國家自然科學基金(41474020；41504010)

王建敏(1973—)，男，碩士，研究方向為空間大地測量數據處理與變形監測。E-mail:wjminlntu@163.com

李亞博。E-mail:liyabo1005@163.com

P228

A

0494-0911(2017)10-0007-05