KILLING VECTOR FIELDS ON COMPACT RIEMANNIAN MANIFOLDS WITH NEGATIVE SCALAR CURVATURE

FU Hai-ping,DAN Ping-ping,PENG Xiao-yun

(1.Department of Mathematics,Nanchang University,Nanchang 330031,China)

(2.Jiangxi Tax Cadre School,Nanchang 330029,China)

KILLING VECTOR FIELDS ON COMPACT RIEMANNIAN MANIFOLDS WITH NEGATIVE SCALAR CURVATURE

FU Hai-ping1,DAN Ping-ping1,PENG Xiao-yun2

(1.Department of Mathematics,Nanchang University,Nanchang 330031,China)

(2.Jiangxi Tax Cadre School,Nanchang 330029,China)

In this paper,we investigate killing vector fields on compact Riemannian manifolds with negative scalar curvature.By using the Bochner method,we obtain a necessary condition of the existence of non-trivial killing vector fields on these manifolds,which extends Theorem 1 due to[6].

killing vector field;negative scalar curvature;trace-free Ricci curvature tensor

1 Introduction

A vector fieldVon a Riemannian manifold(M,g)is Killing if the Lie derivative of the metric with respect toVvanishes as follows

which is equivalent to

where▽denotes the covariant differential operator of(M,g)andX,Y∈TM.This is equivalent to the fact that the one-parameter group of diffeomorphisms associated toVconsists in isometries.Therefore,the space of the non-trivial Killing vector fields for(M,g)in some sense measures the size of the isometry group of(M,g).

The study of killing vector field has a long time.In 1946,Bochner[2]proved that when(M,g)is compact and has negative Ricci curvature,every Killing vector field must vanish.Later,Bochner’s result was extended by Yano to include conformal vector fields[10].It is well known that the existence of non-trivial closed conformal vector fields also imposes many restrictions on a compact Riemannian manifold(see[9]).The Killing vector fieldswere generalized to the Killingp-form and conformal Killingp-form by some authors such as Bochner and Yano,Gallot and Meyer,Tachibana and Yamaguchi,Liu Jizhi and Cai Kairen(see[8]).In 1999,Gursky[5]proved a vanishing theorem for conformal vector fields on four-manifolds of negative scalar curvature,whose assumptions were conformally invariant,and in the case of locally conformally fl at manifolds reduced to a sign condition on the Euler characteristic.The proof due to Gursky is actually are finement of the Bochner method which had been used to prove classical vanishing theorems.Recently,inspired by Gursky’s two papers[4,5],Hu and Li[6]proved Theorem A as follows.

Theorem ALet(M,g)be ann-dimensional compact oriented Riemannian manifold with scalar curvatureR＜0.If there exists a non-trivial Killing vector field on(M,g),then we have

whereEdenotes the trace-free Ricci tensor.Moreover,equality is attained in(1.3)if and only ifRis constant and the Riemannian universal cover of(M,g)is isometric to a Riemannian product R×Nn?1for some Einstein manifoldNn?1with constant scalar curvatureR.

We follow their methods[3,5,6]to improve Theorem A and obtain the following results.

Theorem 1.1Let(M,g)be ann-dimensional compact oriented Riemannian manifold with scalar curvatureR.If there exists a non-trivial Killing vector field on(M,g),then we have

whereEdenotes the trace-free Ricci tensor.Moreover,equality holds in(1.4)if and only ifRis nonpositive constant and the Riemannian universal cover of(M,g)is isometric to a Riemannian product R×Nn?1for some Einstein manifoldNn?1with constant scalar curvatureR.

Corollary 1.2Let(M,g)be ann-dimensional compact oriented Riemannian manifold with scalar curvatureR＜0.If there exists a non-trivial Killing vector field on(M,g),then we have

whereEdenotes the trace-free Ricci tensor.Moreover,equality holds in the above if and only ifRis constant and the Riemannian universal cover of(M,g)is isometric to a Riemannian product R×Nn?1for some Einstein manifoldNn?1with constant scalar curvatureR.

2 Proof of Theorem 1.1

Let(M,g)be ann-dimensional Riemannian manifold.Let{e1,···,en}with respect to the Riemannian metricgbe a local orthonormal basis ofTM,and{θ1,···,θn}be its dual basis.Let{θij}be the connection forms of(M,g),one has the structure equations

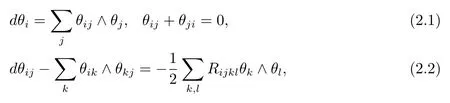
whereRijklare the components of the Riemannian curvature tensor of(M,g).The Ricci curvature tensorRijand the scalar curvatureRof(M,g)are de fined by

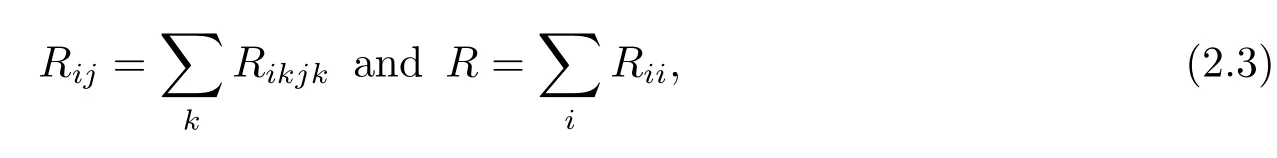
respectively.For a vector fieldon(M,g),we de fine the covariant derivativeVi,jand the second covariant derivativeVi,jk,respectively,byi.e.,

and

Using exterior derivation of(2.4),one gets the Ricci identity

From(2.5)and(2.7),we have

and thus for anyk,

Combing(2.6),(2.7)with(2.8),we get the following Weitzenb?ck formula(see[1])

Lemma 2.1Letbe a Killing vector field on then-dimensional Riemannian manifold(M,g).Then we have

Remark 2.2In[5],Gursky observed that(2.10)still holds for every conformal vector fieldV.In[6],Hu and Li proved Lemmas 2.1 and 2.3.For completeness,we write the proofs of Hu and Li.

ProofIt suffices to prove(2.10)for any fixed pointp∈?0:={x∈M|V(x)≠0}.Note that on ?0,(2.10)is equivalent to

Aroundp,we choose{ei}such thatV(p)=V1(p)e1(p);that is,V2=···=Vn=0 atp.From(2.7),we have

Then atp,we have

This proves(2.10),or equivalently proves(2.11)on ?0.

Combing(2.6)and(2.7)with(2.8),we have

Form(2.12)and the unique continuation result of Kazdan[7],we know that,for a nontrivial Killing vector fieldVon the compact Riemannian manifold(M,g),the setM?0is of measure zero.Combining this fact with(2.9)and(2.11),one has the following lemma.

Lemma 2.3LetVbe a non-trivial Killing vector field on a compact Riemannian manifold(M,g).Then holds onMin the sense of distributions.

In order to prove Theorem 1.1,we need the following algebraic lemma,which can be proved by the standard method of Lagrange multipliers,and was observed by Hu and Li[6].

Lemma 2.4LetA=(aij)n×nbe areal symmetric matrix withandx1,···,xn∈R.Then

and(x1,···,xn)correspondingly takes the value((n?1)λ,0,···,0),whereλ ＞0 holds if there is equality in the right-hand side of(2.14),andλ＜0 holds if there is equality in the left-hand side of(2.14).

Proof of Theorem 1.1Letbe a non-trivial Killing vector field on(M,g).Denote byEthe trace-free part of the Ricci tensor Ric,i.e.,Eij=Rij?(R/n)δij.Then,applying Lemma 2.4,we get that

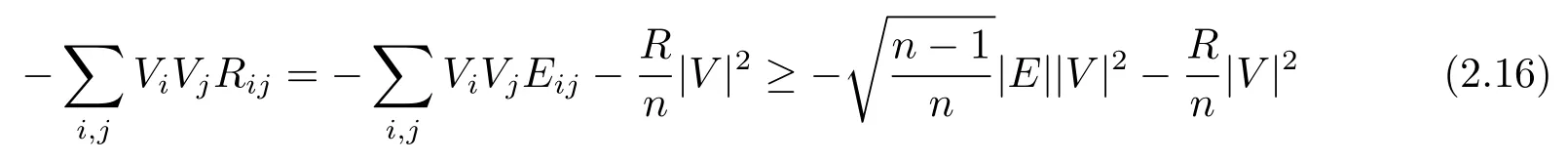
and the second equality holds at a pointp∈MwithV(p)≠0 if and only if by choosing suitable{ei},Ecan be diagonalized as

correspondingly,V1=(n?1)λandV2=...=Vn=0 for someλ ＞0.

Combining(2.13)with(2.16),we get

Forε＞0,we de fine a functionThus we

From(2.18)and(2.19),we directly compute

and thus

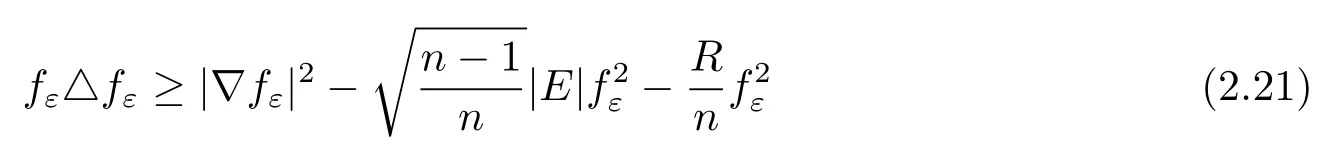
and thus

Integrating(2.22)onM,we obtain

i.e.,

If the equality holds in(2.23),then equality(2.16)must hold at each point ofM.Thus at each point ofM,Ecan be diagonalized as in(2.17).So it satisfies

Furthermore,combining(2.17)with(2.24)givesλ=?R/n(n?1).Then we must haveV1=?R/n,V2=...=Vn=0 and

Remark 2.5We see that ifR＜0,one has

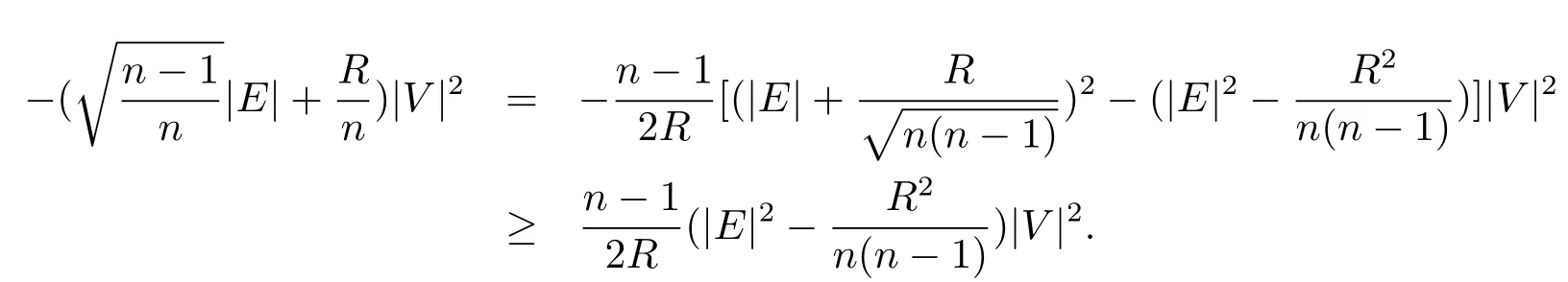
Then

holds onMin the sense of distributions.Hence Corollary 1.2 can be considered as generalization of Theorem 1 in[6],i.e.,Theorem A.

[1]Besse A L.Einstein manifolds[M].Berlin:Springer-Verlag,1987.

[2]Bochner S.Vector field and Ricci cuvature[J].Bull.Amer.Math.Soc.,1946,52:776–797.

[3]Fu Haiping.On compact manifolds with harmonic curvature and positive scalar curvature[J].J.Geom.Anal.,DOI:10.1007/s12220-017-9798-z.

[4]Gursky M J.The Weyl fuctional,de Rham cohomology,and K?hler-Einstein metrics[J].Ann.Math.,1998,148:315–337.

[5]Gursky M J.Confomal vector fields on four-manifolds with negative scalar curvature[J].Math.Z.,1999,232:265–273.

[6]Hu Zejun,Li Haizhong.Scalar curvature,killing vector fields and harmonic one-forms on compact Riemannian manifolds[J].Bull.London Math.Soc.,2004,36:587–598.

[7]Kazdan J.Unique continuation in geometry[J].Comm.Pure Appl.Math.,1988,41:667–681.

[8]Liu Jizhi,Cai Kairen.The duality of conformal Killingp-forms on Riemannian manifolds[J].J.Math.,1990,10(2):157–160.

[9]Tanno S,Weber W.Closed conformal vector fields[J].J.Di ff.Geom.,1969,3:361–366.

[10]Yano K.On harmonic and Killing vector fields[J].Ann.Math.,1952,55:38–45.

具有負數量曲率的緊致黎曼流形的Killing向量場

付海平1,但萍萍1,彭曉蕓2
(1.南昌大學數學系,江西南昌 330031)
(2.江西省稅務干部學校,江西南昌 330029)

本文研究了具有負數量曲率的緊致黎曼流形上的Killing向量場.利用Bochner方法,得到在此類流形上非平凡的Killing向量場的存在的必要條件.這個結果拓廣了文獻[6]中的定理1.

Killing向量場;負數量曲率;無跡Ricci曲率張量

O186.12

53C20;53C24

A

0255-7797(2017)06-1118-07

date:2016-09-02Accepted date:2016-11-17

Supported by the National Natural Science Foundations of China(11261038;11361041).

Biography:Fu Haiping(1975–),male,born at Xiajiang,Jiangxi,associate professor,major in differential geometry.