ON THE SUM OF k-POWER OF ALL DISTANCES IN BIPARTITE GRAPHS

GENG Xian-ya,ZHAO Hong-jin,XU Li-li

(1.School of Mathematics and Big Data,Anhui University of Science and Technology,Huainan 232001,China)

(2.School of Mathematics and Statistics,Central China Normal University,Wuhan 430079,China)

ON THE SUM OFk-POWER OF ALL DISTANCES IN BIPARTITE GRAPHS

GENG Xian-ya1,ZHAO Hong-jin1,XU Li-li2

(1.School of Mathematics and Big Data,Anhui University of Science and Technology,Huainan 232001,China)

(2.School of Mathematics and Statistics,Central China Normal University,Wuhan 430079,China)

Denote the sum ofk-power of all distances between all pairs of vertices inGbySk(G).In this paper,by applying the vertex partition method,sharp bound of all connectednvertex bipartite graphs of diameterdon theSk(G)is obtained,and the extremal graphs with the minimalSk(G)are also characterized.

bipartite graph;diameter;extremal graph

1 Introduction

In this paper,we only consider connected,simple and undirected graphs and assume that all graphs are connected,and refer to Bondy and Murty[2]for notation and terminologies used but not de fined here.

LetG=(VG,EG)be a graph with vertex setVGand edge setEG.G?v,G?uvdenote the graph obtained fromGby deleting vertexv∈VGor edgeuv∈EG,respectively(this notation is naturally extended if more than one vertex or edge is deleted).Similarly,G+uvis obtained fromGby adding an edgeuv/∈EG.Forv∈VG,letNG(v)(N(v)for short)denote the set of all the adjacent vertices ofvinGandd(v)=|NG(v)|,the degree ofvinG.

A bipartite graphGis a simple graph,whose vertex setVGcan be partitioned into two disjoint subsetsV1andV2such that every edge ofGjoins a vertex ofV1with a vertex ofV2.A bipartite graph in which every two vertices from different partition classes are adjacent is called complete,which is denoted byKm,n,wherem=|V1|,n=|V2|.

The distanced(u,v)between verticesuandvinGis de fined as the length of a shortest path between them.The diameter ofGis the maximal distance between any two vertices ofG.LetBdnbe the class of all bipartite graphs of ordernwith diameterd.

LetSk=Sk(G)be the sum ofk-power of distances between all pairs of vertices ofG,which is denoted by

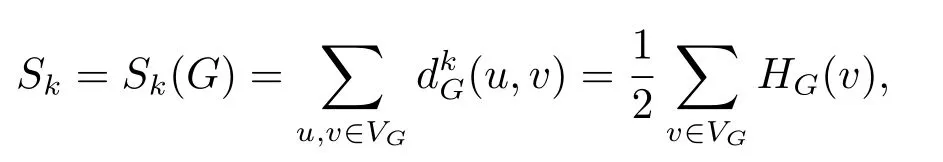
whereHG(v)is the sum ofk-power of all diatances fromvinG.

Whenk=1,Skis Wiener index.The Wiener index is popular in chemical literatures.This quantity was introduced by Mustapha Aouchich and Pierre Hansen in[1]and was extensively studied in the monograph.Recently,S2(G)is applied to the research of distance spectral radius.Zhou and Trinajsti?[19]proved an upper bound using the ordernin addition to the sum of the squares of the distancesS2(G),see[18,20].They also proved a lower bound on the distance spectral radius of a graph using onlyS2(G).As a continuance of it,in this paper,we determine the extremal graphs with the minimalSk(G)for the class of all connectedn-vertex bipartite graphs of diameterd.For surveys and some up-to-date papers related to Wiener index of trees and line graphs,see[7,9,11–15,17]and[3,6,8,10,16],respectively.

In this paper we study the quantitySkin the case ofn-vertex bipartite graphs,which is an important class of graphs in graph theory.Based on the structure of bipartite graphs,sharp bounds onSkamongBdnare determined.The corresponding extremal graph is also identified.

Further on we need the following lemma,which is the direct consequence of the de finition ofSk.

Lemma 1.1LetGbe a connected graph of ordernand not isomorphic toKn.Then for each edgeSk(G)＞Sk(G+e).

2 The Graph with Minimum Skamong Bdn

LetGbe a graph inClearly there exists a partitionV0,V1,···,VdofVGsuch that|V0|=1 andd(u,v)=ifor each vertexv∈Viandu∈V0(i=0,1,···,d).We callVia block ofVG.Two blocksVi,VjofVGare adjacent if|i?j|=1.For convenience,let|Vi|=lithroughout this section.

Lemma 2.1[15]For any graphwith the above partition ofVG,G[Vi]induces an empty graph(i.e.,containing no edge)for eachi∈(i=0,1,···,d).

Given a complete bipartite graphwith bipartition(X,Y)satisfyingandchoose a vertexx(resp.y)inX(resp.Y)and let?xy,whereG′is depicted in Figure 1.LetG?be the graph obtained fromG′by attaching pathsandatxandy,respectively.It is routine to check thatfor oddd.

Given a complete bipartite graphKp,qwith bipartition(X,Y)satisfying|X|=p≥3,|Y|=q≥2,andp+q=n?d+4,choose two different vertices,sayx,yinXand let

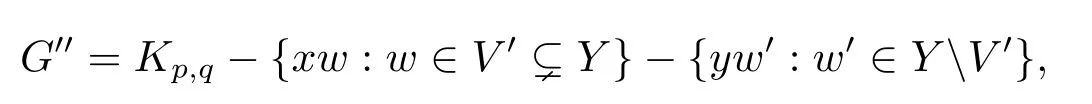
whereG′′is depicted in Figure 1.Letbe the graph obtained fromG′′by attaching pathsandatxandy,respectively.It is routine to check thatfor evend.Set

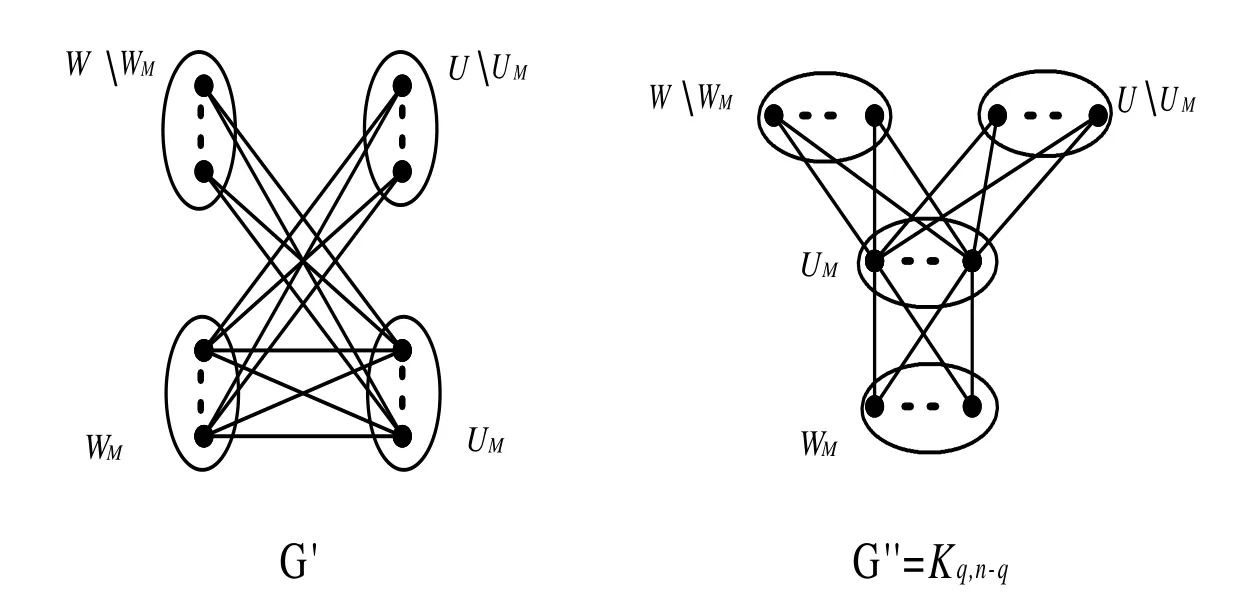
Figure 1:Graphs G′and G′′

Theorem 2.2LetGbe inwith the minimumSk(G).

(i)Ifd=2,then

(ii)Ifd≥3,thenG≌G?for odddandG∈B for evend,whereG?and B are de fined as above.

ProofChooseG∈Bdnwith bipartition(X,Y)such thatSk(G)is as small as possible.

(i)Ifd=2,then by Lemma 1.1,G≌Kn?t,t,wheret≥2 orn?t≥2.Let|X|=n?t,|Y|=t.Then it is routine to check that,for allx(resp.y)inX(resp.Y),one has

which gives

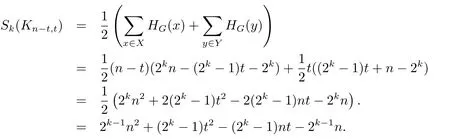
Ifnis odd,thenwith equality if and only if,o r,i.e.And ifnis even,thenwith equality if and only ifi.e.,,as desired.

(ii)First we show the following facts.

Fact 1G[Vi?1,Vi]induces a complete bipartite subgraph for eachi∈(0,1,···d),and|Vd|=1 ford≥3.

Proof of Fact 1The first part follows directly from Lemmas 1.1 and 2.1.So in what follows,we prove the second part.

Letd≥3,z∈Vdandw∈Vd?3.If|Vd|＞2,thenG+zw∈BdnandV0∪V1∪Vd?3{w}∪Vd?2∪Vd?1∪{w}∪Vdis a partition ofVG+zw.By Lemma 1.1Sk(G+zw)＜Sk(G),a contradiction.

This completes the proof of Fact 1.

Fact 2Consider the vertex partitionVG=V0∪V1∪···∪VdofG.

(i)Ifdis odd,then

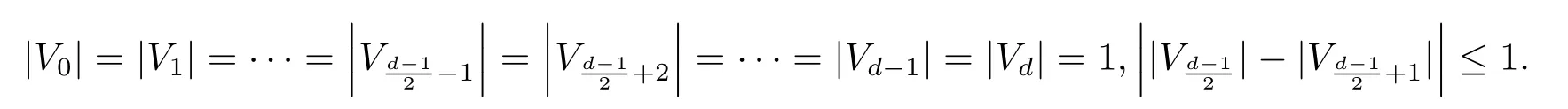
(ii)Ifdis even,then

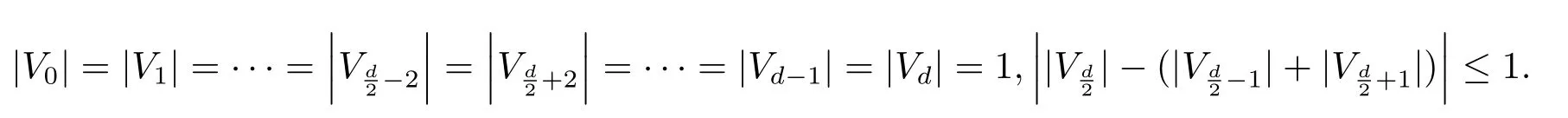
Proof of Fact 2(i)Note thathere we only show that|V1|=1 holds.Similarly,we can also showwe omit the procedure here.

In fact,ifd=3,our result is trivial.So we consider thatd≥5.If|V1|≥2,then chooseu∈V1and letG′=G?v0u+{ux:x∈V4}.In fact,the vertex partition ofG′isV0∪V1{u}∪V2∪V3∪{u}∪V4∪···∪Vd,in view of Fact 1 and the choice ofG,any two of adjacent blocks ofVG′induce a complete bipartite subgraph and|Vd|=1 ford≥5.

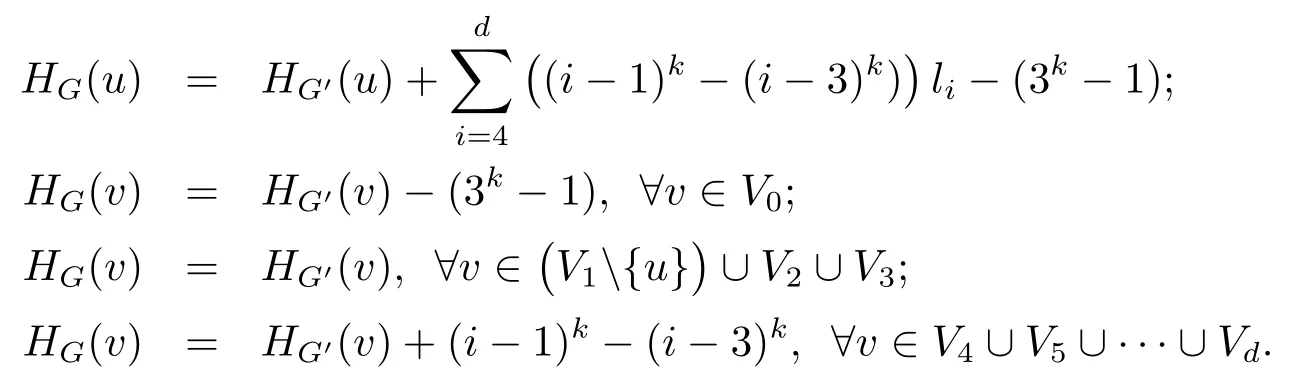
This gives

i.e.,Sk(G)＞Sk(G′),a contradiction to the choice ofG.Hence,|V1|=1.

Next we show that ifdis odd,thenWithout loss of generality,we assume thatThen it suffices to show thatIf this is not true,thenChooselet

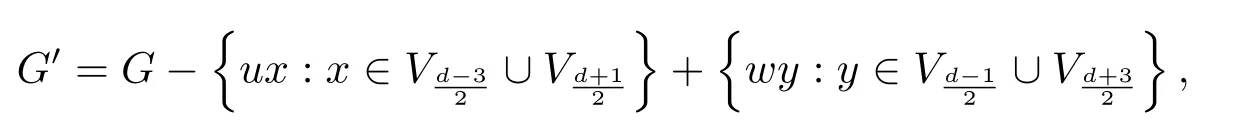
then the vertex partition ofG′is

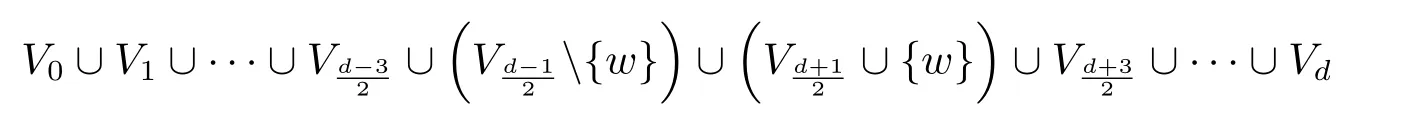
and each of the two adjacent blocks ofVG′induces a complete bipartite graph.By direct calculation,we have

a contradiction to the choice ofG.

(ii)By the same discussion as the proof of the first part of(i)as above,we can show thatwe omit the procedure here.

Now,we show that ifdis even,thenWithout loss of generality,we assume thatThen it suffices to show that

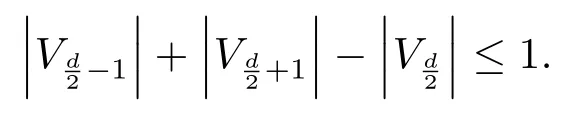
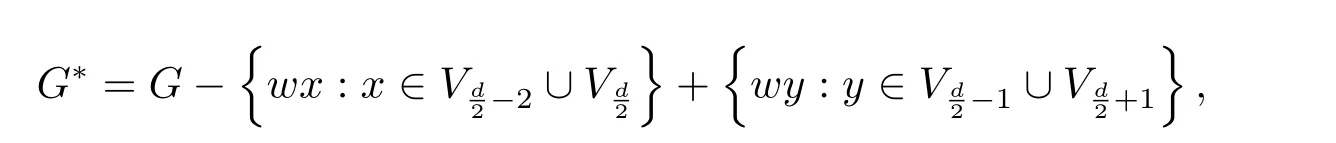
then the vertex partition ofG?is

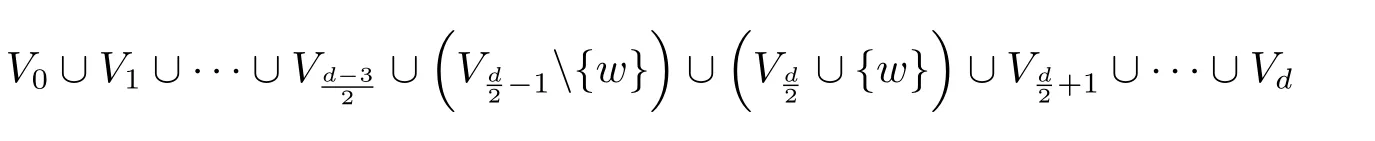
and each of the two adjacent blocks ofVG?induces a complete bipartite graph.By direct calculation,we have

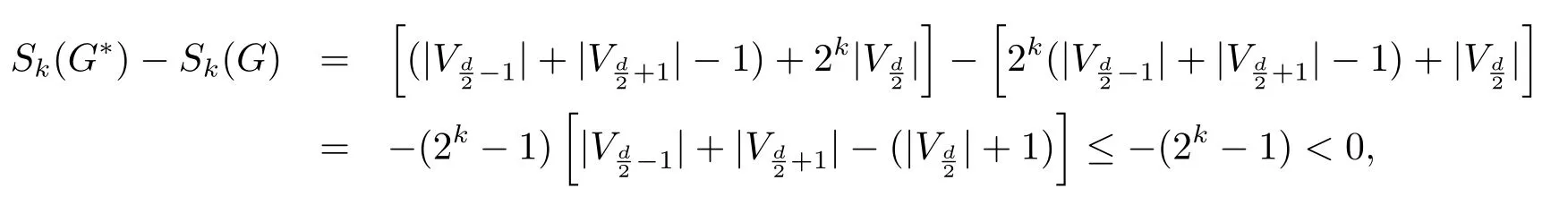
a contradiction to the choice ofG.

This completes the proof of Fact 2.

Now we come back to show the second part of Theorem 2.2.In view of Fact 2(i),ifdis odd,note thattogether withwe obtain thatas desired.

In view of Fact 2(ii),ifdis even,note thattogether withwe obtain thatG∈B.Furthermore,

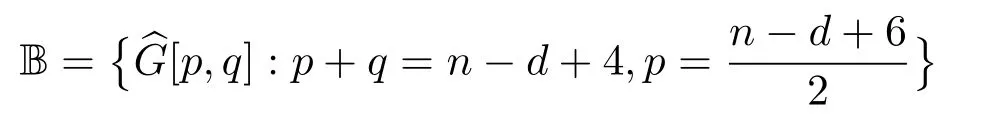
for evennandfor oddn.

This completes the proof.

[1]Mustapha Aouchiche,Pierre Hansen.Distance spectra of graphs:a survey[J].Lin.Alg.Appl.,2014,458:301–386.

[2]Bondy J A,Murty U S R.Graph theory[M].GTM,Vol.224,American:Springer,2008.

[3]Cohen N,Dimitrov D,Krakovski R,et al.On Wiener index of graphs and their line graphs[J].MATCH Commun.Math.Comput.Chem.,2010,64:683–698.

[4]Wang T,Wu L X.Decomposition of planar graphs without 5-cycles orK4[J].J.Math.,2016,36(2):223–233.

[5]Zhang X E,Jiang W.Complements of distance-regular graphs[J].J.Math.,2016,36:234–238.

[6]Dankelmann P,Gutman I,Mukwembi S,et al.The edge-Wiener index of a graph[J].Disc.Math.,2009,309:3452–3457.

[7]Dobrynin A,Entringer R,Gutman I.Wiener index of trees:theory and applications[J].Acta Appl.Math.,2001,66:211–249.

[8]Don Y,Bian Y,Gao H,et al.The polyphenyl chains with extremal edge-Wiener indices[J].Match Commun.Math.Comput.Chem.,2010,64:757–766.

[9]Gutman I,Klav?ar S,Mohar B,et al.Fifty years of the Wiener index[J].Match Commun.Math.Comput.Chem.,1997,3:51–259.

[10]Iranmanesh A,Kafrani A S.Computation of the first edge-Wiener index ofTUC4C8(S)nanotube[J].Match Commun.Math.Comput.Chem.,2009,62:311–352.

[11]Li S C,Song Y B.On the sum of all distances in bipartite graphs[J].Disc.Appl.Math.,2014,169:176–185.

[12]Liu M,Liu B.On the variable Wiener indices of trees with given maximum degree[J].Math.Comput.Model.,2010,52:1651–1659.

[13]Luo W,Zhou B.On ordinary and reverse Wiener indices of non-caterpillars[J].Math.Comput.Model.,2009,50:188–193.

[14]Merris R.An edge version of the matrix-tree theorem and the Wiener index[J].Lin.Multi.Alg.,1988,25:291–296.

[15]Pisanski T,?erovnik J.Edge-contributions of some topological indices and arboreality of molecular graphs[J].Ars.Math.Contemp.,2009,2:49–58.

[16]Wu B.Wiener index of line graphs[J].Match Commun.Math.Comput.Chem.,2010,64:699–706.

[17]Zhang X D,Liu T,Han M X.Maximum Wiener index of trees with given degree sequence[J].Match Commun.Math.Comput.Chem.,2010,64:661–682.

[18]Zhou B,Trinajsti? N.Mathematical properties of molecular descriptors based on distances[J].Croat.Chem.Acta,2010,83:227–242.

[19]Zhou B,Trinajsti? N.On the largest eigenvalue of the distance matrix of a connected graph[J].Chem.Phys.Lett.,2007,447:384–387.

[20]Zhou B,Trinajsti? N.Further results on the largest eigenvalues of the distance matrix and some distance based matrices of connected(molecular)graphs[J].Intern.Elec.J.Mol.Des.,2007,6:375–384.

[21]Zhang H H,Li S C,Zhao L F.On the further relation between the(revised)Szeged index and the Wiener index of graphs[J].Discr.Appl.Math.,2016,206:152–164.

二部圖的距離k次方和問題

耿顯亞1,趙紅錦1,徐李立2
(1.安徽理工大學數學與大數據學院,安徽淮南 232001)
(2.華中師范大學數學與統計學院,湖北武漢 430079)

本文定義Sk(G)為G中所有點對之間距離的k次方之和.利用頂點劃分的方法得到了直徑為d的n頂點連通二部圖Sk(G)的下界,并確定了達到下界所對應的的極圖.

二部圖;直徑;極圖

O157.6

05C50;05C35

A

0255-7797(2017)06-1111-07

date:2017-01-08Accepted date:2017-04-01

Supported by National Natural Science Foundation of China(11401008;61672001;61572035;61402011)and China Postdoctoral Science Foundation(2016M592030).

Biography:Geng Xianya(1981–),male,born at Fuyang,Anhui,associate professor,major in graph theory and its application.