基于EC法的風浪聯合作用主塔-基礎體系極限荷載效應

涂志斌，黃銘楓，樓文娟

(浙江大學 建筑工程學院結構工程研究所，杭州 310058)

基于EC法的風浪聯合作用主塔-基礎體系極限荷載效應

涂志斌，黃銘楓，樓文娟

(浙江大學 建筑工程學院結構工程研究所，杭州 310058)

針對基于Rosenblatt映射變換的極限狀態曲線計算困難的現狀，提出了多維隨機變量極限狀態曲線的簡化算法。該算法通過尋找同時滿足邊緣分布、聯合分布和可靠指標的變量估計值，將隨機變量條件分布函數及其逆函數的求解轉化為邊緣分布函數的求逆，從而達到簡化極限狀態曲線計算的目的。以某跨海大橋橋塔-基礎體系為工程實例，以潿洲島海洋站風浪同步觀測資料為環境變量統計資料，通過基于Copula函數的聯合分布模型構造了風浪聯合分布函數，根據簡化算法計算了風浪極限狀態曲線，利用EC法估計了橋塔-基礎體系的基底剪力極限荷載效應，并與外推法的估計結果進行了比較。結果表明，基于簡化算法和EC法的跨海大橋橋塔-基礎體系基底剪力極限荷載效應具有較高的準確性。

極限荷載效應；極限狀態曲線；風浪聯合作用；EC法；Copula函數

跨海大橋在施工和運營過程中將承受復雜的、隨時間變化的隨機環境作用，主要包括風和波浪。為使結構在使用期內正常發揮預定功能，采用極限荷載效應進行結構設計十分必要[1-2]。

在極限荷載效應估計中，構造聯合分布函數是考慮多維隨機環境變量聯合作用的有效方法。多位學者采用傳統聯合分布模型來構造多維隨機環境變量的聯合分布函數[3-7]。然而該模型要求變量服從同類邊緣分布，相關關系采用Pearson線性相關系數表達，適用范圍有限。基于Copula函數的聯合分布模型彌補了傳統聯合分布模型的不足。該模型將邊緣分布和相關關系分開考慮，不要求變量服從同類邊緣分布，可描述任意相關關系，具有極強的靈活性，在多維變量聯合分布函數構造中的應用十分廣泛[8-15]。

在基于概率的結構設計方法中，外推法是多維隨機環境變量聯合作用下極限荷載效應分析的有效方法，具有較高的可信度和適應性，但需在環境變量分布范圍內進行結構動力有限元分析，計算效率較低[16]。為提高極限荷載效應的估計效率，Winterstein等[17-18]在外推法的基礎上提出了EC(Environmental Contour)法。EC法的核心思想是在具有指定超越概率的環境變量極限狀態曲面上搜尋極限荷載效應及其對應的環境變量組合點，結構動力有限元分析只需在極限狀態曲面上完成，效率大大提高。Haver等[19-23]利用EC法估計了多維隨機環境變量聯合作用下工程結構的極限荷載效應。然而在EC法中，極限狀態曲面的估計依賴于環境變量條件分布函數及其逆函數的求解。當聯合分布函數較為復雜時，條件分布函數及其逆函數的求解十分困難，極限狀態曲面的計算難以實現，EC法的適應性較低。Montes-Iturrizaga欲根據Copula函數的性質提出極限狀態曲面的簡化算法[24]，但在推導過程中不恰當地利用了聯合分布函數與Copula函數的關系。

為提高EC法的適應性，本文提出了極限狀態曲面的簡化算法。以某跨海大橋橋塔-基礎體系為工程實例，以潿洲島海洋站的風浪同步觀測資料為環境變量統計資料，通過Copula函數構造了風浪聯合分布函數，根據簡化算法計算了風浪極限狀態曲線，利用EC法估計了橋塔-基礎體系的基底剪力極限荷載效應，并與外推法的估計結果進行了比較，討論了EC法的適用范圍。

1 基于Copula函數的聯合分布模型

Copula函數是一種構造聯合分布的工具，其優勢是將變量間的相關關系與邊緣分布分開考慮，能適應任意多維隨機變量的聯合分布分析。二維隨機變量聯合分布函數與Copula函數的關系為

F(s1,s2)=C[F1(s1),F2(s2),θ]

(1)

式中:F(s1,s2)為隨機變量s1、s2的聯合分布函數；C[·]為Copula函數；F1(s1)、F2(s2)為s1、s2的邊緣分布函數；θ為二者的相關系數，能衡量隨機變量間的任意相關關系。對式(1)等號兩側同時求二階混合偏導，可得到聯合概率密度函數f(s1,s2)與Copula函數的關系

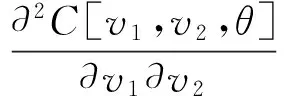
(2)

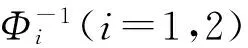
在眾多Copula函數中，同時滿足以下兩個條件的Copula函數稱為最優Copula：①v1、v2能準確描述s1、s2的邊緣分布特性；②θ能準確描述各隨機變量間的相關關系。目前常用的最優Copula評價準則為AIC準則和BIC準則[26-27]。二者則均建立在Copula函數參數估計的基礎上，表達式分別為

(3)

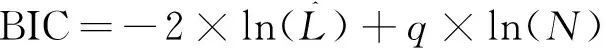
(4)

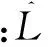
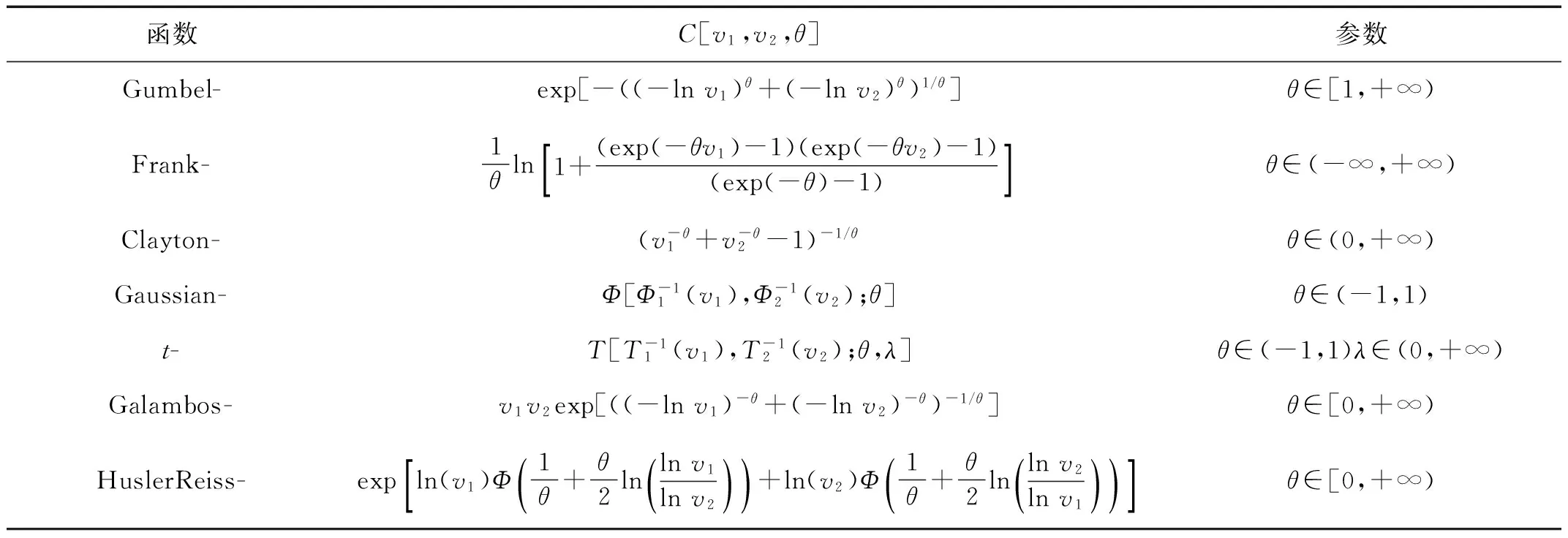
表1 常用的Copula函數Tab.1 Common Copula functions

2 基于EC法的極限荷載效應

2.1EC法的基本原理

EC法的核心思想是在超越概率為pE的環境變量極限狀態曲面上搜尋極限荷載效應及其對應的環境變量組合點。與外推法在整個環境變量分布范圍內完成結構動力有限元分析不同，EC法只需要在極限狀態曲面上完成分析，計算效率大大提高。EC法有兩個基本假定：①荷載效應極值的變異性可以忽略，②環境變量極限狀態曲面為線性凸曲面。根據假定，超越概率為pE的極限荷載效應是相同超越概率下極限狀態曲面上的最大荷載效應極值中位值。

本節仍以二維隨機變量來說明EC法的基本原理和實施步驟，此時極限狀態曲面退化為極限狀態曲線。對于具有相關性的隨機變量s1、s2，直接在物理空間中計算二者的極限狀態曲線并不容易。根據Rosenblatt映射變換，具有任意相關關系的隨機變量都可轉換為標準正態空間中的獨立隨機變量，即

Φ1(u1)=F1(s1),Φ2(u2)=F2|1(s2)

(5)

(6)

式中:u1、u2為標準正態空間中相互獨立的隨機變量，服從標準正態分布；F2|1(s2)為s2的條件分布函數，與s2的邊緣分布特性及s1和s2的相關關系有關。根據式(5)和式(6)，標準正態空間中的極限狀態曲線u1-u2可轉換為物理空間中的極限狀態曲線s1-s2。若將s2看作主變量，s1看作條件變量，式(6)可改寫為

(7)

理論上式(6)和式(7)是等價的，以s2為主變量、s1為條件變量不會改變極限狀態曲線的估計結果。因此本節分析在式(6)的基礎上展開。在標準正態空間中，極限狀態曲線u1-u2為半徑等于可靠指標βT的圓

(8)

βT=-Φ-1(PE)

(9)

式中,ω為角坐標。式(9)說明了可靠指標βT與超越概率PE的關系。

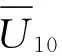
圖1詳細說明了風、浪聯合作用下基于EC法的極限荷載效應lT的計算流程，包含4個主要步驟，如4個虛線框所示。①根據重現期T計算超越概率PE和可靠指標βT。②在[0,2π)范圍內離散ω，離散點數為m；根據式(8)計算標準正態空間中的極限狀態曲線離散點(u1,i,u2,i)；根據式(6)轉換為物理空間中的離散點(ui,hi)。③調整隨機數cj來完成離散點(ui,hi)處的隨機流場同步模擬，包括脈動風速和隨機波浪；生成隨機荷載時程，完成結構動力有限元計算，并根據POT法提取荷載效應極值Lj。當k次結構動力有限元計算完成時，擬合Lj的分布函數，取分布函數值為0.5時的荷載效應極值為中位值Lm,i。④重復③直至i=m，在m個中位值Lm,i中尋找最大值，作為超越概率為PE的極限荷載效應lT。在該流程中離散點(ui,hi)的計算是難點。在EC法中，極限狀態曲線上的結構動力有限元計算次數為k×m。為進一步提高極限荷載效應lT的估計效率并保證準確性，極限狀態曲線的離散應遵循以下原則：在中位值Lm,i較大的區域加密離散點，在Lm,i較小的區域減少甚至不設置離散點。

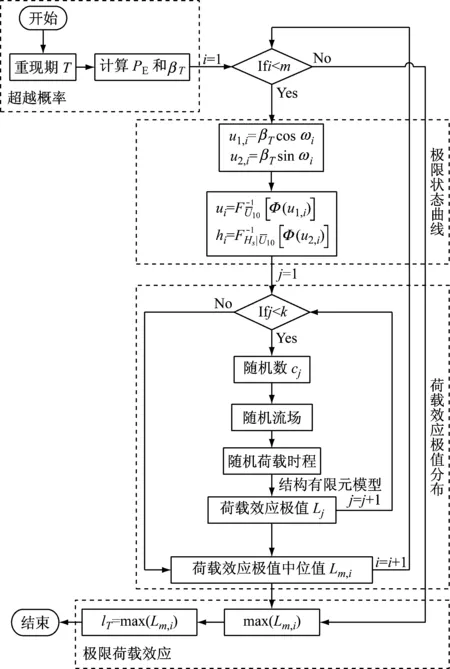
圖1 基于EC法的極限荷載效應lT計算流程Fig.1 Flow chart of extreme load effect lT based on EC method

一般而言，基于POT(Peak Over Threshold)的數據樣本服從廣義帕累托分布(Generalized Pareto Distribution，GPD)或三參數威布爾分布(Three-Parameter Weibull Distribution，W3P)[28]，二者的表達式分別為

GPD

F0,POT(lT)=1-(1-kglT/ag)kg≠0

F0,POT(lT)=1-exp(-lT/ag)kg=0

(10)

W3P

(11)

式中:ag、aw為尺度參數;kg、kw為形狀參數;μw為位置參數。荷載效應極值分布函數F0(lT)與F0,POT(lT)的關系為

F0(lT)=[F0,POT(lT)]nPOT

(12)

式中,nPOT為荷載效應極值L的樣本容量。

2.2極限狀態曲線的簡化算法

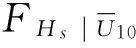
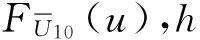
(13)

結合式(1)和式(5)有

(14)

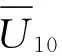
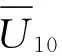
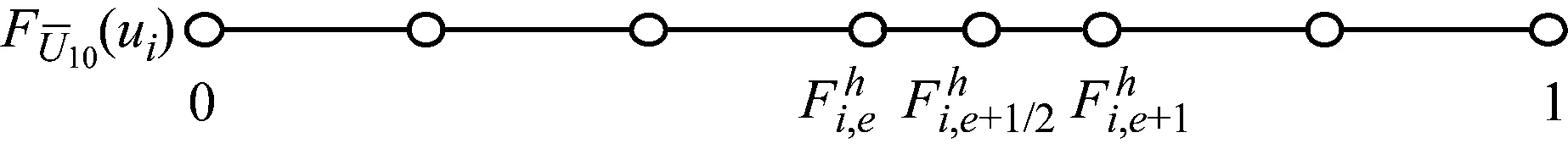
圖2 網格劃分示意圖
Fig.2 Grid meshing

3 工程背景

3.1風浪同步觀測資料

(15)

式中:s=u、h;Fs(s)為邊緣分布函數;μs為位置參數;σs為尺度參數。子樣1、子樣2的邊緣分布參數擬合結果見表2。

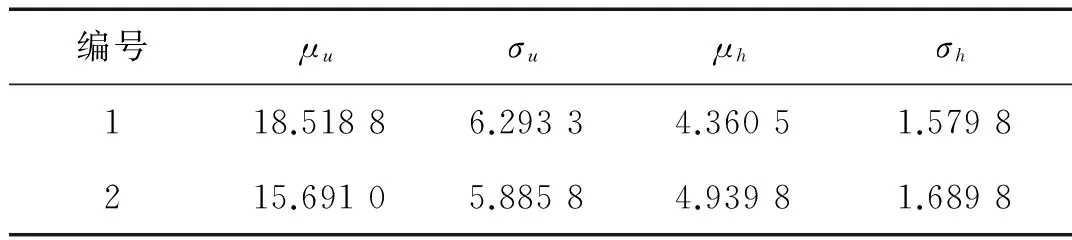
表2 邊緣分布函數的參數擬合值Tab.2 Fitted values of marginal CDF

從表1中選擇最優Copula來構造子樣1、子樣2的聯合分布函數。采用極大似然法估計Copula函數的參數，采用AIC準則和BIC準則選擇最優Copula，結果見表3和表4。對于子樣1、子樣2，兩種準則的評價結果一致，即Gaussian Copula為最優Copula，參數θ的擬合值分別為0.745 5、0.605 6。圖3和圖4為子樣1、子樣2的聯合概率密度，符號Y表示考慮風浪相關性(θ≠0)，N表示不考慮風浪相關性(θ=0)。由圖可知，子樣1/2-Y的聯合概率密度峰值大于子樣1/2-N。根據Turkstra法則及其拓展[29-30]，子樣1、子樣2為所有樣本的上下邊界。因此基于子樣1、子樣2的極限荷載效應是基于其他樣本的極限荷載效應的上下邊界。

表3Copula函數的擬合參數、AIC及BIC：子樣1
Tab.3Fttedparameters,AICandBICofCopulafunctionsofsubsample1

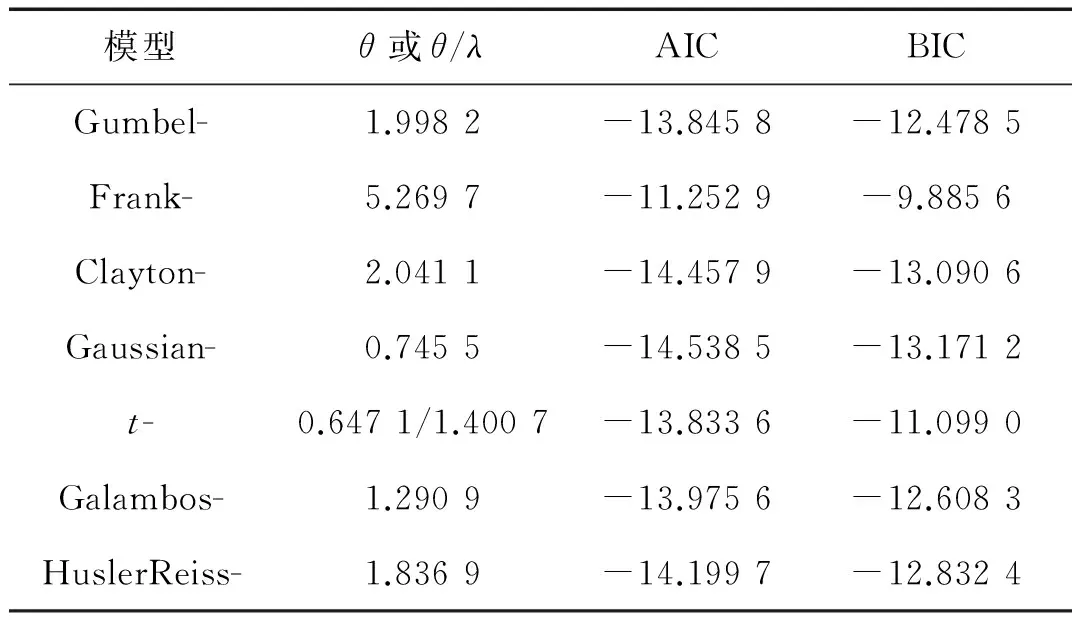
模型θ或θ/λAICBICGumbel-1.9982-13.8458-12.4785Frank-5.2697-11.2529-9.8856Clayton-2.0411-14.4579-13.0906Gaussian-0.7455-14.5385-13.1712t-0.6471/1.4007-13.8336-11.0990Galambos-1.2909-13.9756-12.6083HuslerReiss-1.8369-14.1997-12.8324

3.2橋塔-基礎體系

某跨海大橋橋塔-基礎為鋼筋混凝土結構，混凝土

表4Copula函數的擬合參數、AIC及BIC：子樣2
Tab.4Fittedparameters,AICandBICofCopulafunctionsofsubsample2

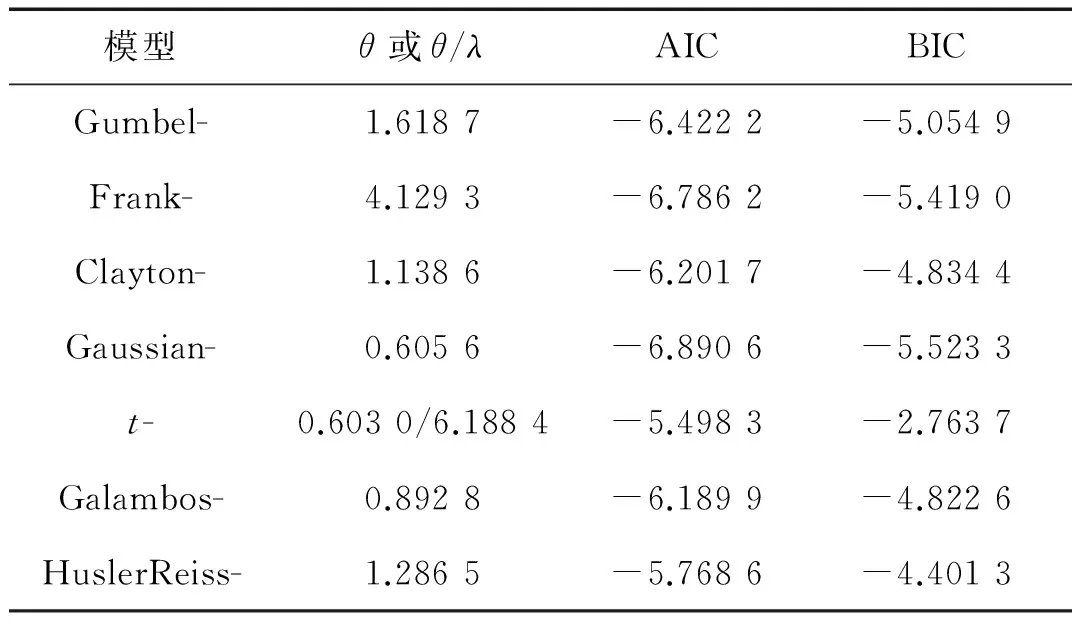
模型θ或θ/λAICBICGumbel-1.6187-6.4222-5.0549Frank-4.1293-6.7862-5.4190Clayton-1.1386-6.2017-4.8344Gaussian-0.6056-6.8906-5.5233t-0.6030/6.1884-5.4983-2.7637Galambos-0.8928-6.1899-4.8226HuslerReiss-1.2865-5.7686-4.4013

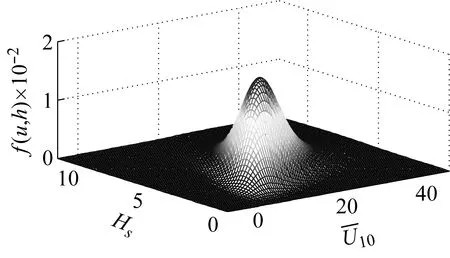
(a) 子樣1-Y

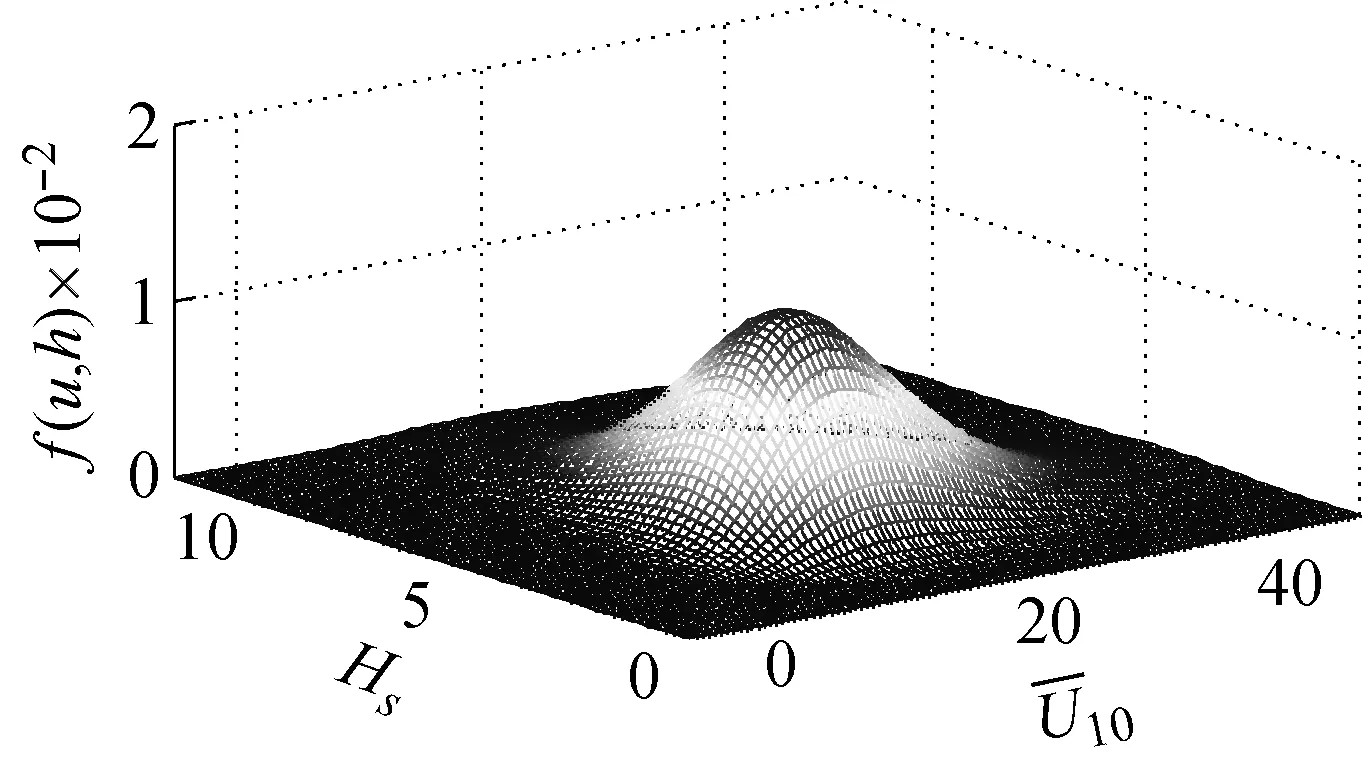
(b) 子樣1-N圖3 子樣1的聯合概率密度函數Fig.3 JPDF of subsample 1

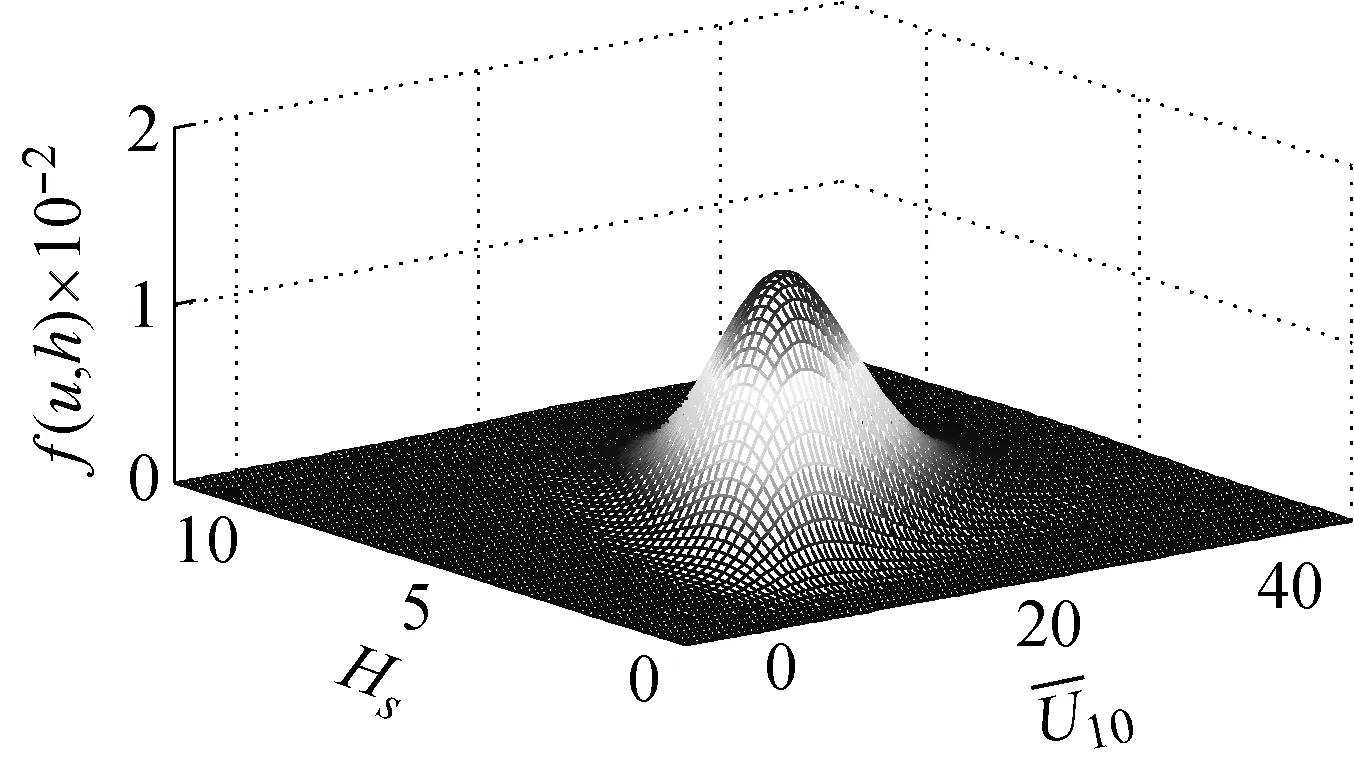
(a) 子樣2-Y

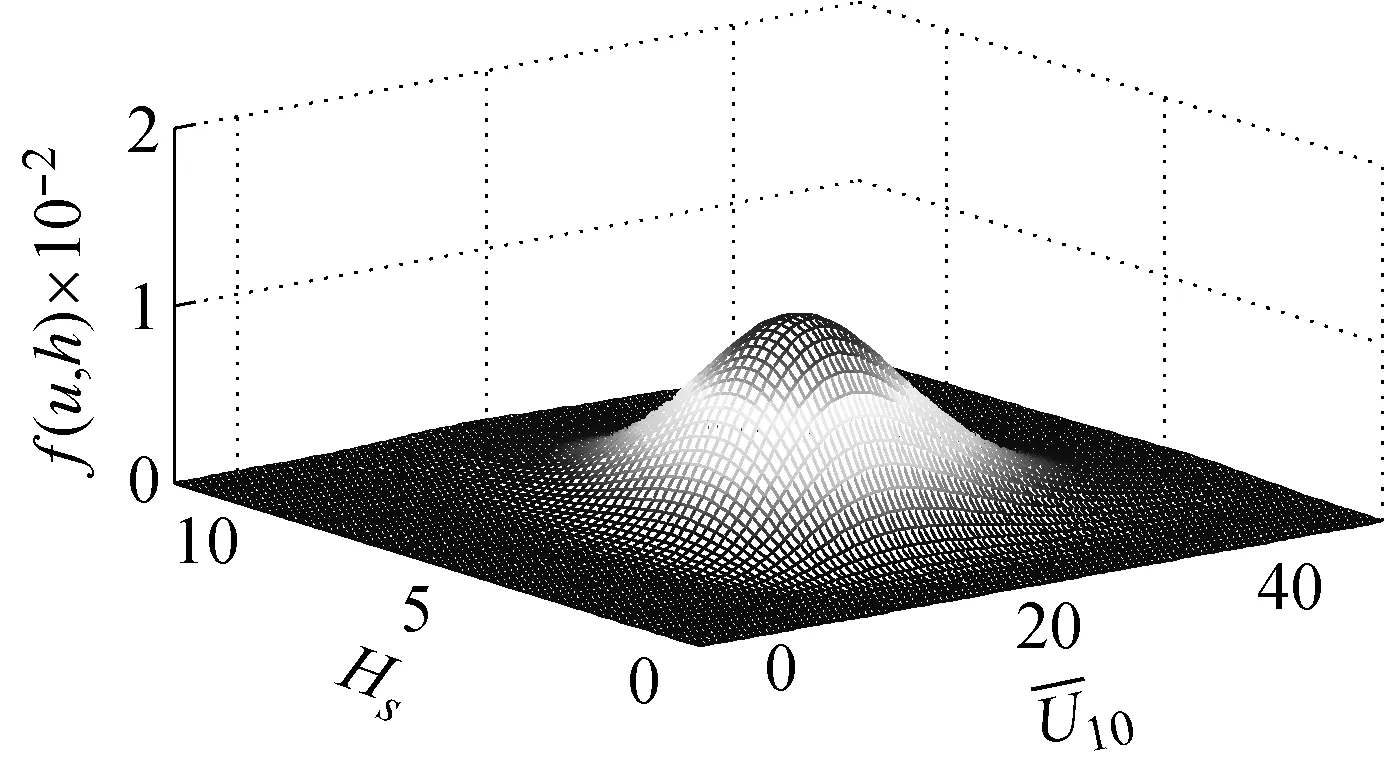
(b) 子樣2-N圖4 子樣2的聯合概率密度函數Fig.4 JPDF of subsample

的強度等級為C40。橋塔為鉆石型，高460 m，位于水面以上；橋塔89 m處設有4道高9 m、寬4 m的橫梁；橋塔截面尺寸沿高度逐漸變化，其中x、y方向上塔底中心間距為28 m、40 m，塔底尺寸為20 m、16 m，塔頂尺寸為15 m、14 m；橫梁以下塔腿內、外側x方向上的傾斜度為5.70∶1、8.39∶1，y方向上的傾斜度為4.78∶1、6.21∶1，橫梁以上塔腿內、外側x方向上的傾斜度為15.46∶1、17.73∶1，y方向上的傾斜度為11.53∶1、10.95∶1。基礎由沉井和承臺組成，位于水面以下。沉井為大直徑圓形沉井，直徑90 m，井壁厚2.5 m；沉井內部x、y方向上等間距地設有5道厚度為1.5 m的隔墻；沉井頂部為承臺，厚度7 m；泥面以上基礎的總高度為50 m。借助ANSYS軟件建立橋塔-基礎體系的有限元模型，如圖5。橋塔采用空間梁單元模擬，沉井和承臺采用三維實體單元模擬，在橋塔和承臺的接觸面處建立剛性區域以傳遞自由度。沉井底部采用固定端約束。表5為橋塔-基礎體系的前三階模態信息。

表5 橋塔-基礎體系的模態信息Tab.5 Mode shapes of bridge-tower system

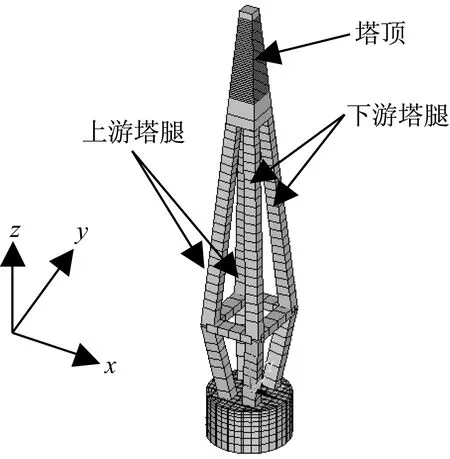
圖5 橋塔-基礎體系有限元模型Fig.5 Finite element model of tower-basement system

4 基底剪力極限荷載效應

4.1極限狀態曲線

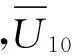
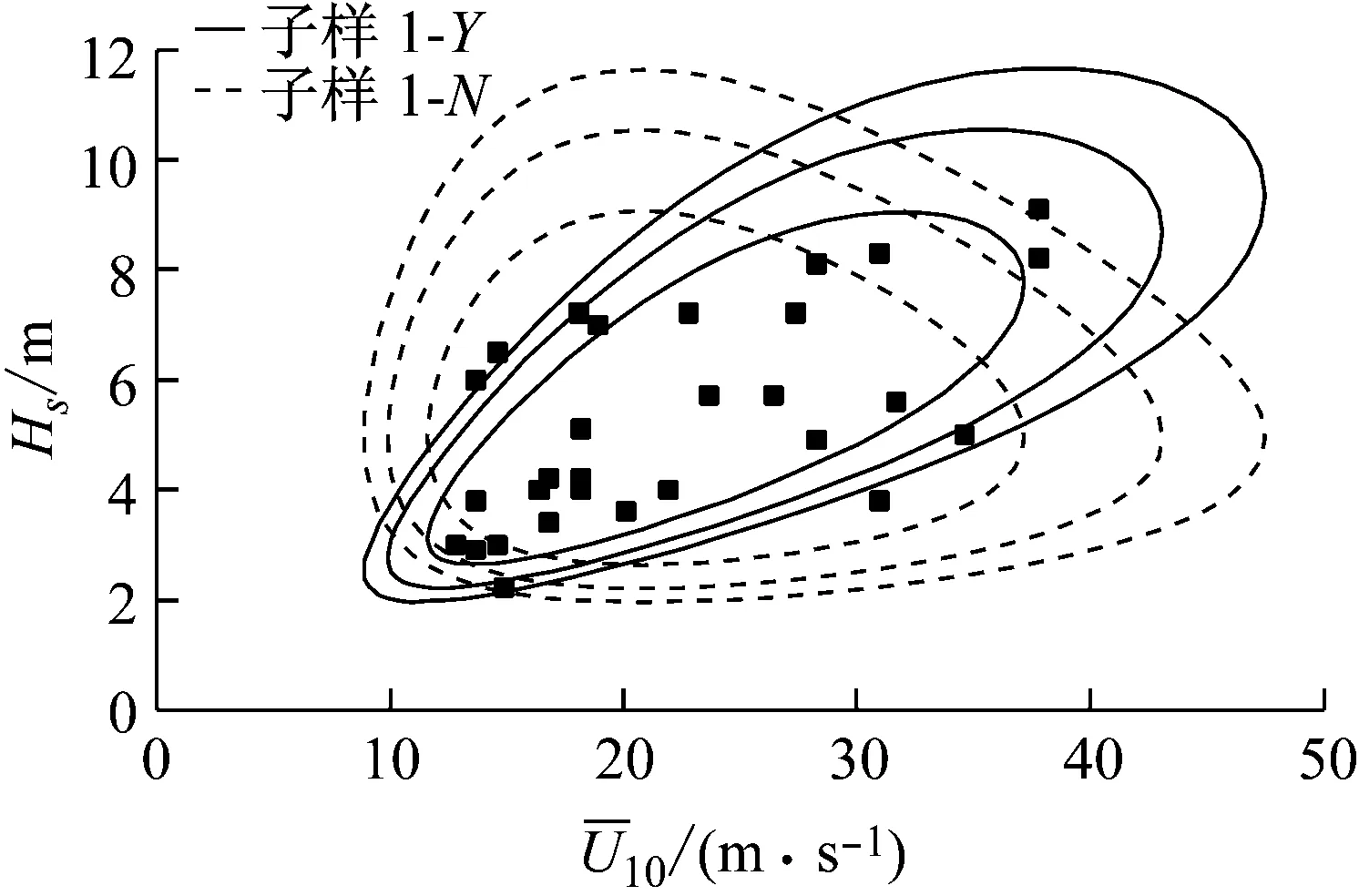
(a) 子樣1

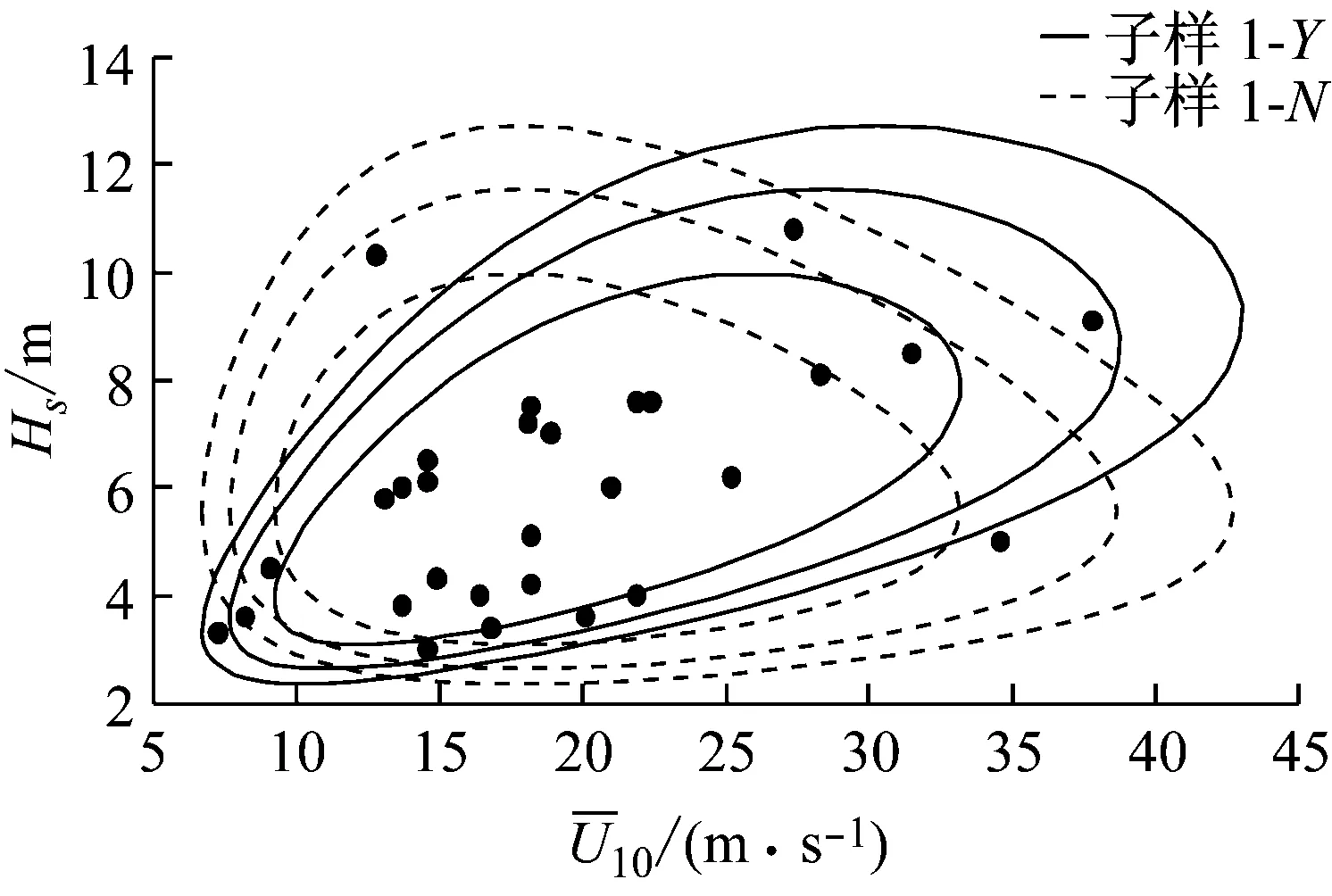
(b) 子樣2圖6 子樣1、子樣2的極限狀態曲線Fig.6 Limit state lines of subsample 1 and 2

4.2橋塔-基礎體系的輸入荷載

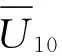
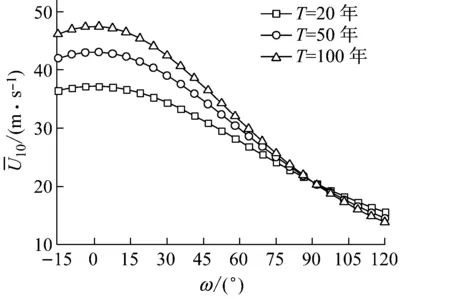
(a) 主變量

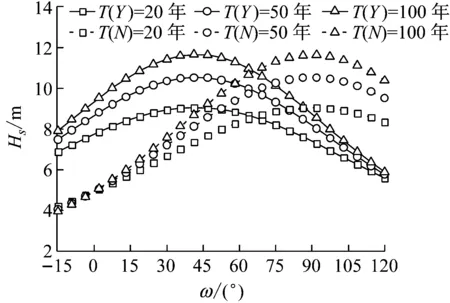
(b) 條件變量Hs圖7 子樣1平均風速和有效波高Hs離散點Fig.7 Discrete points of and Hs for subsample 1

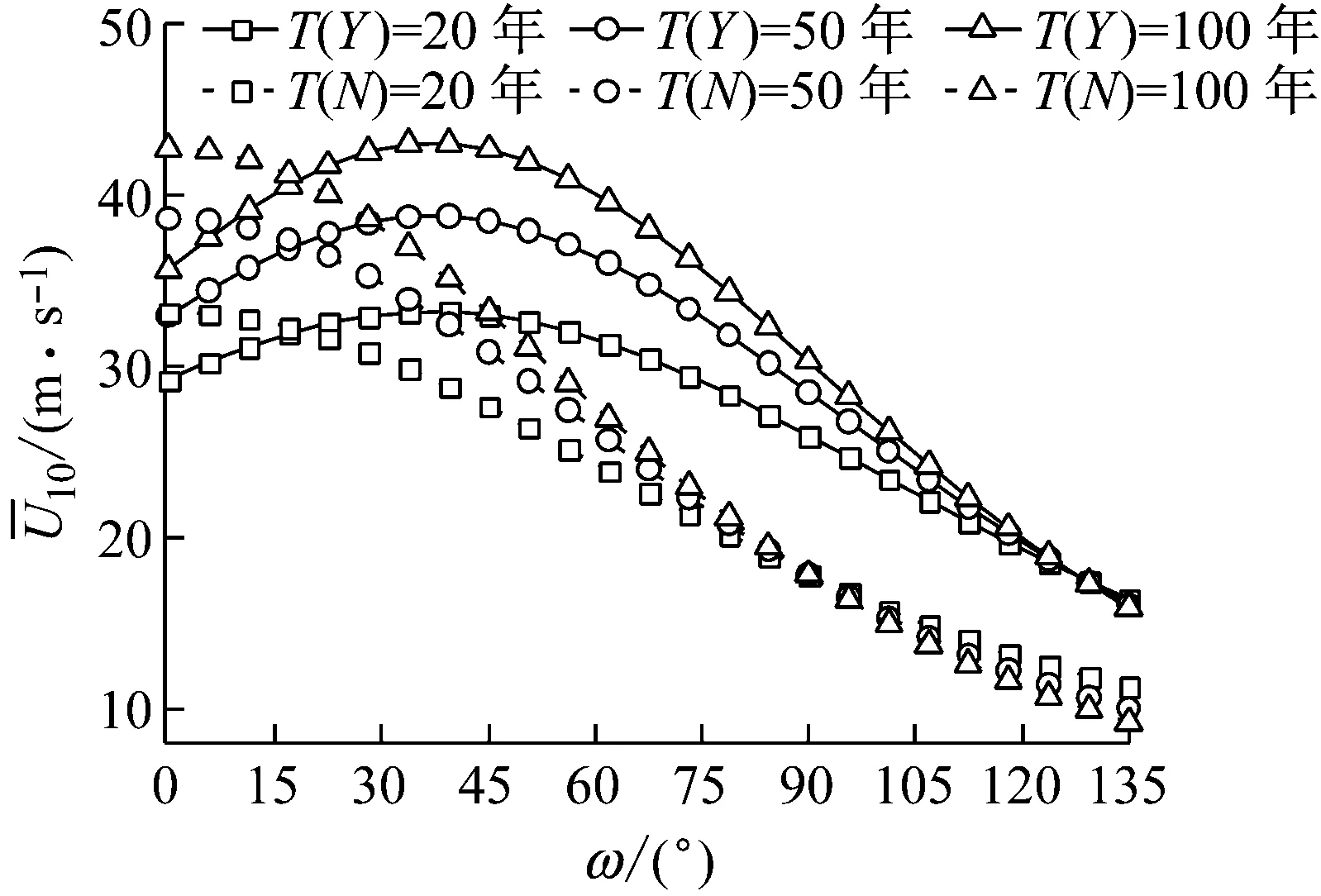
(a) 條件變量

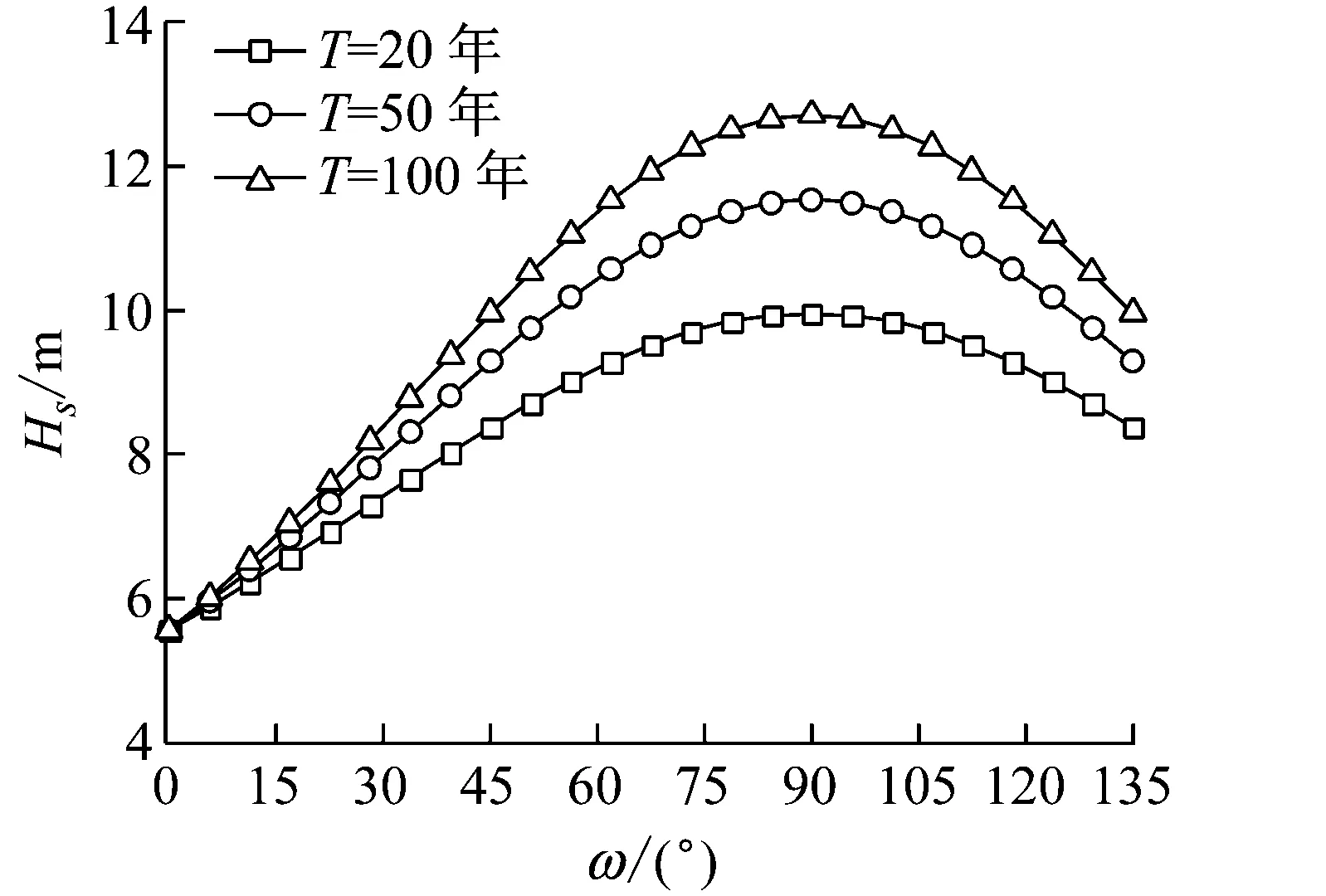
(b) 主變量Hs圖8 子樣2平均風速和有效波高Hs離散點Fig.8 Discrete points of and Hs for subsample 2

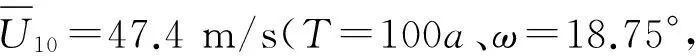
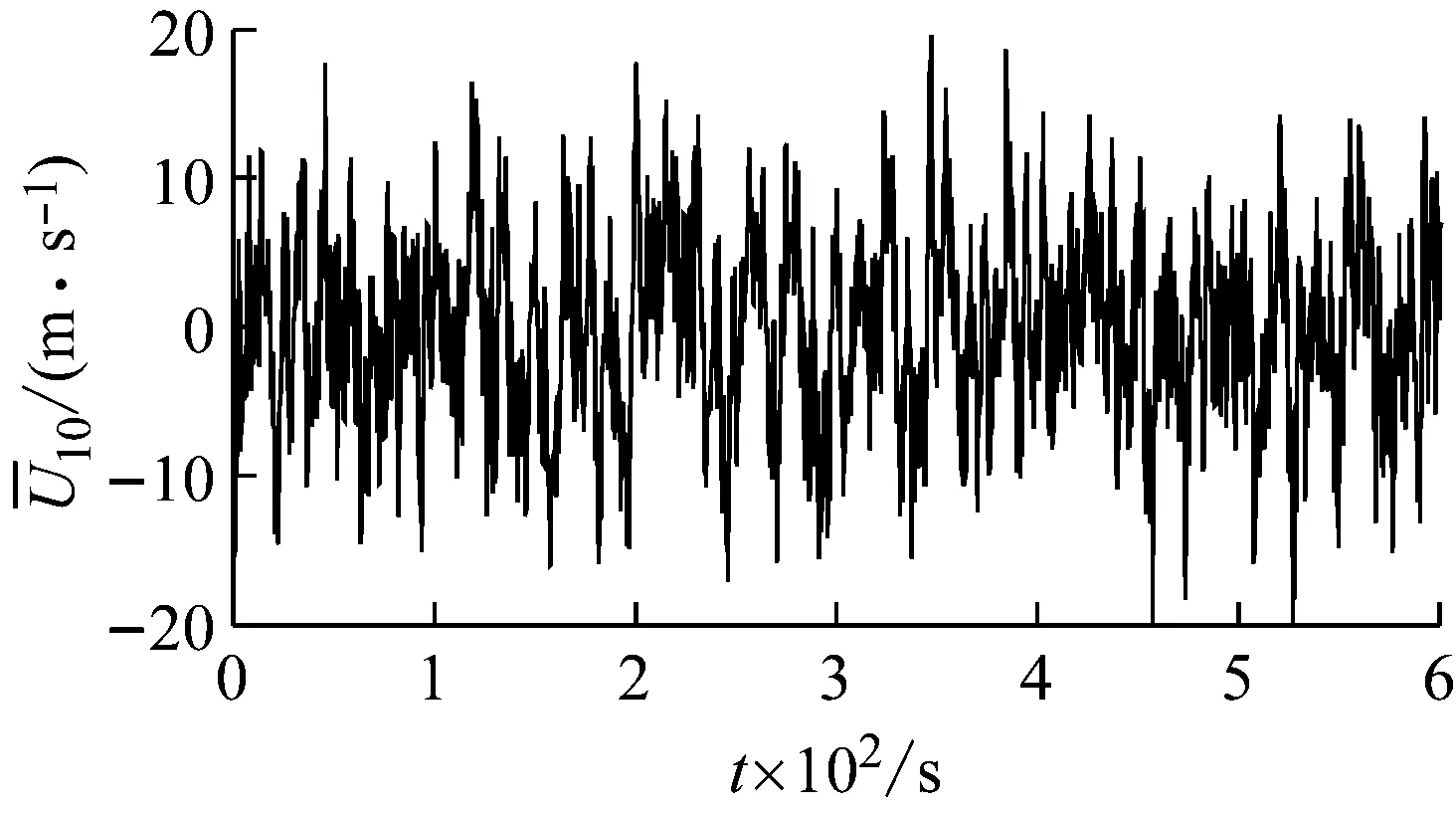
圖9 脈動風速時程Fig.9 History of fluctuating wind speed: =47.4 m/s

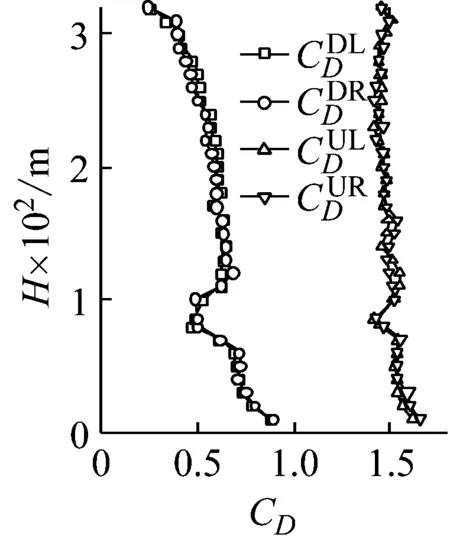
(a) 塔腿部分

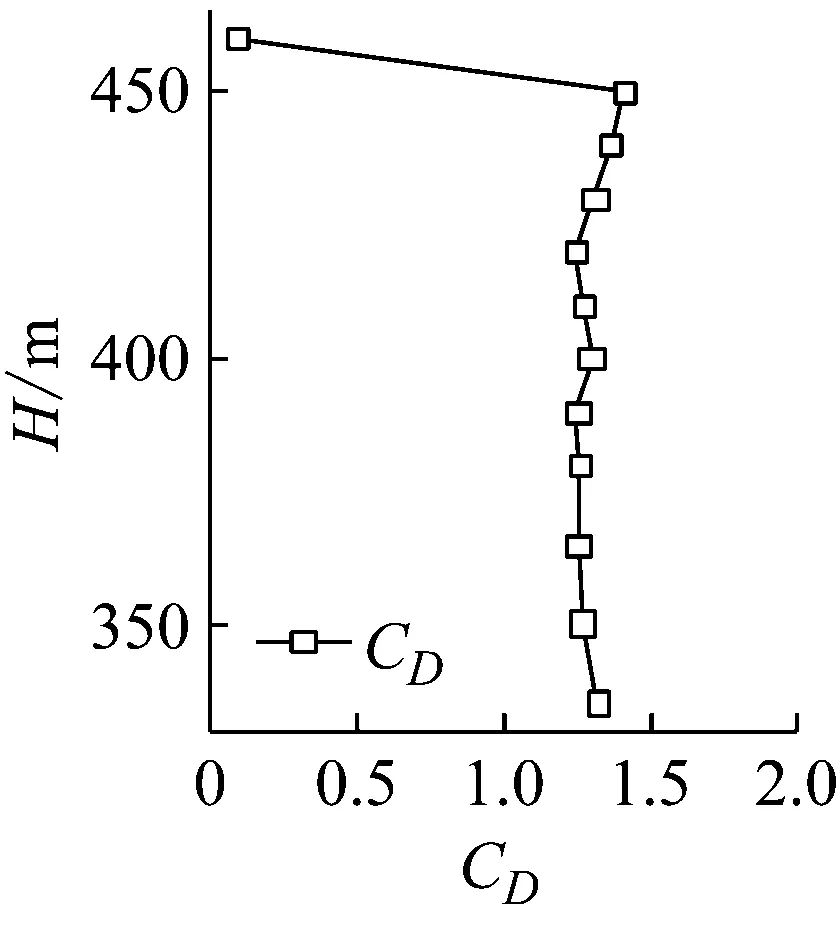
(b) 塔頂部分圖10 橋塔阻力系數CDFig.10 Drag force coefficients CD of bridge tower

隨機波浪的模擬參數見表6，Ts為有效周期，γ為譜峰因子。圖11為模擬隨機波面時程，此時Hs=10.8 m(T=100a、ω=18.75°，考慮風浪相關性)。作用在基礎上的隨機波浪壓力可根據繞射理論計算。

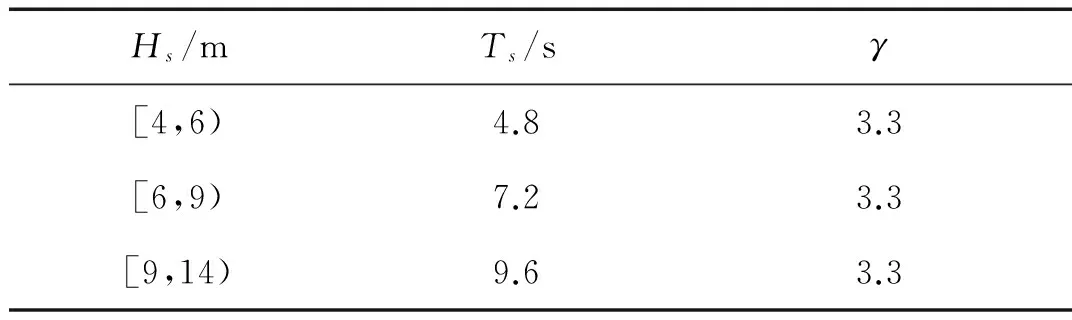
表6 隨機波浪模擬參數Tab.6 Simulation parameters of random wave height

在時域內完成橋塔-基礎體系的動力有限元分析，橋塔的輸入荷載為風荷載時程，基礎的輸入荷載為隨機波浪壓力時程，分析方法為完全瞬態法。根據DNV(Det Norske Veritas)[32]的研究成果，風浪聯合作用時風向與波向的差異很小。跨海大橋所在地的氣象資料顯示，橋位處的常年風向以NW為主，與模型坐標y軸一致。因此風攻角和波浪入射方向均與y軸一致。

圖11 隨機波浪時程：Hs=10.8 mFig.11 History of random wave height: Hs=10.8 m

4.3荷載效應極值分布函數

根據IEC 61400-1的建議，離散點處的結構動力有限元重復計算次數取k=6，閾值取6條荷載效應時程的均值與1.4倍標準差之和。結合極限狀態曲線的離散點數，本文共完成了k×m=150次有限元計算。

圖12 基底剪力時程Fig.12 History of base shear force: =47.4 m/s、Hs=10.8 m

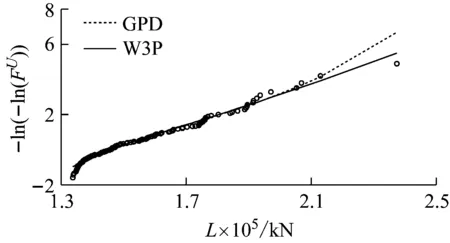
圖13 荷載效應分布函數Fig.13 CDF of base shear force: =47.4 m/s、Hs=10.8 m

4.4極限荷載效應

圖14為各離散點處荷載效應極值中位值Lm,i的變化規律。由圖可知：①隨離散點的變化，Lm,i無突變且變化軌跡為拋物線；②考慮風浪相關性時，各重現期下子樣1、子樣2的max(Lm,i)分別出現在ω=22.5°、78.75°；③不考慮風浪相關性時，各重現期下子樣1、子樣2的max(Lm,i)分別出現在ω=78.75°、84.375°。這表明極限狀態曲線離散點的設置是合理的。為了進一步減小計算量，提高極限荷載效應lT的估計效率，離散點的分布范圍和數量可進一步減少。

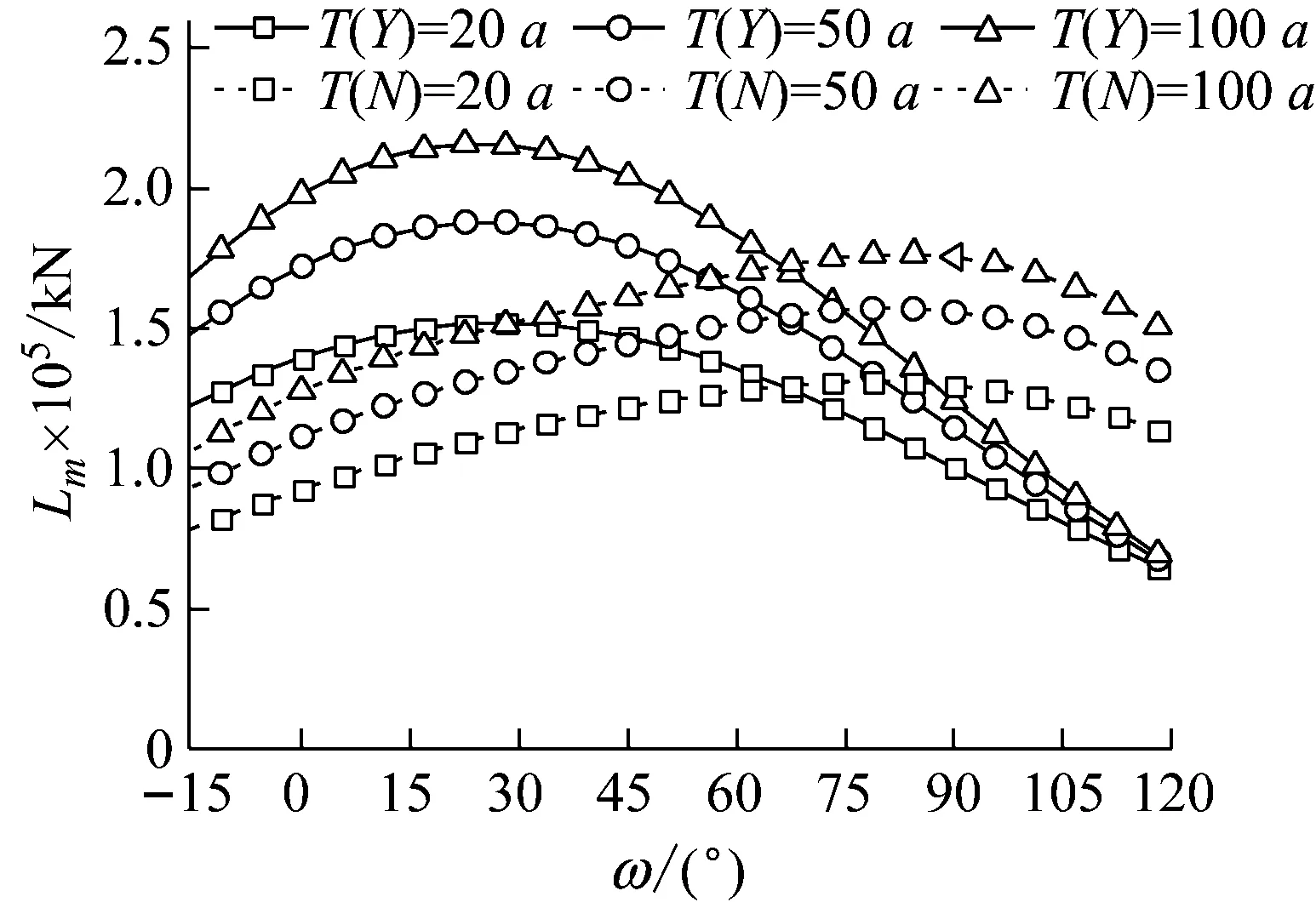
(a) 子樣1

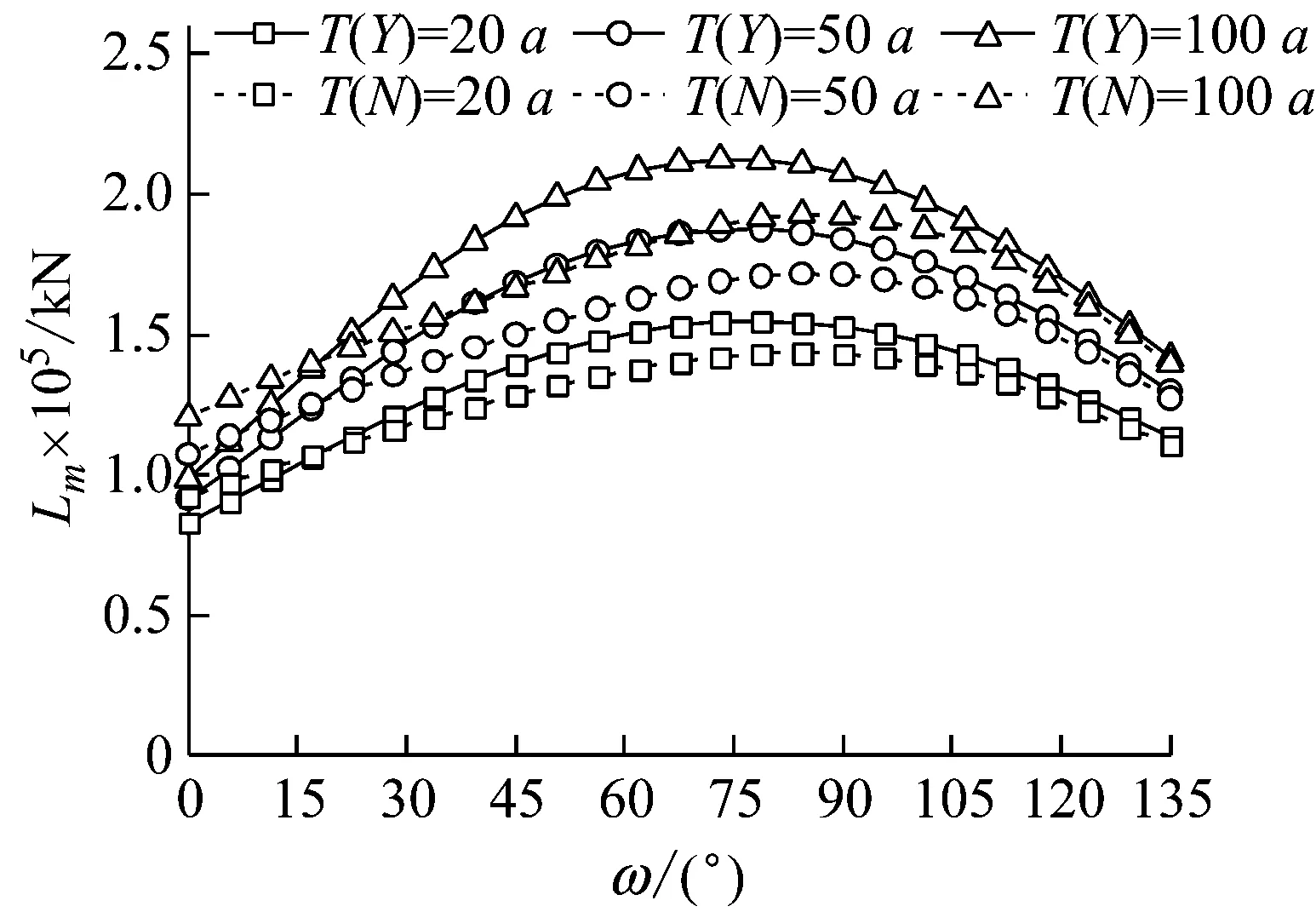
(b) 子樣2圖14 各離散點處的荷載效應極值中位值Lm,iFig.14 Medians Lm,i of peak load effect at discrete points

基于EC法的極限荷載效應lT將與基于外推法的lT進行對比。由于不引入任何假定，基于外推法的計算結果具有較高的可信度，可作為基于EC法的計算結果的對比標準。基于外推法的橋塔-基礎體系基底剪力極限荷載效應lT的具體實現和計算結果參考涂志斌等[33]的文章。涂志斌等指出采用外推法估計lT時，風浪分布范圍內的橋塔-基礎體系動力有限元計算次數為432，而本文的計算次數為150。因此與外推法相比，EC法的計算效率顯著提高。事實上，通過合理地設置離散點，橋塔-基礎體系的動力有限元計算次數還可進一步降低，EC法的計算效率也可進一步提高。

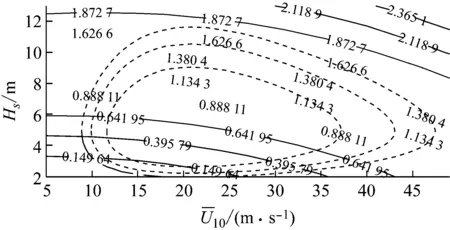
(a) 子樣1-N

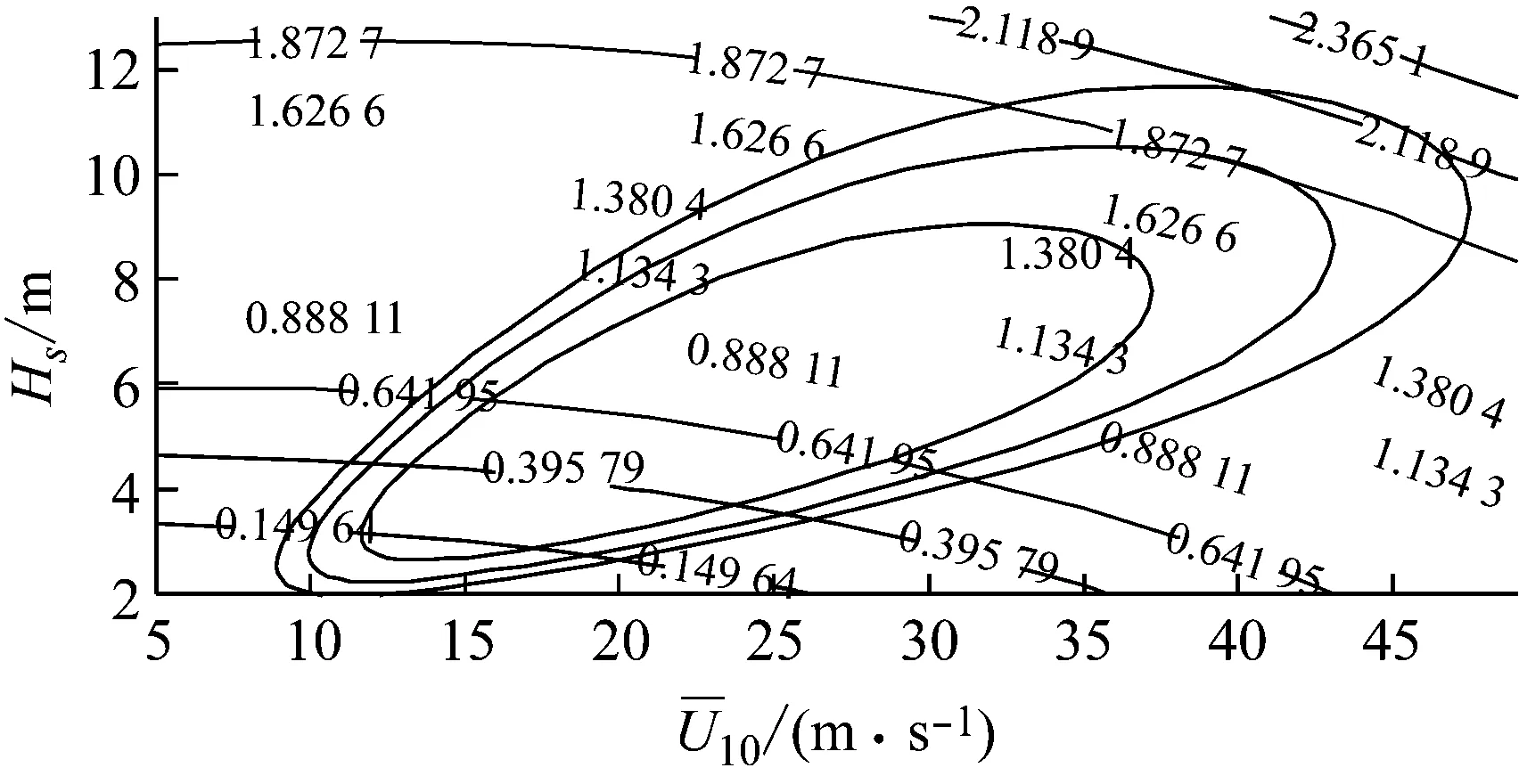
(b) 子樣1-Y圖15 荷載效應極值中位值Lm,i的等值線：子樣1Fig.15 Contours of peak load effect medians Lm,i: subsample 1

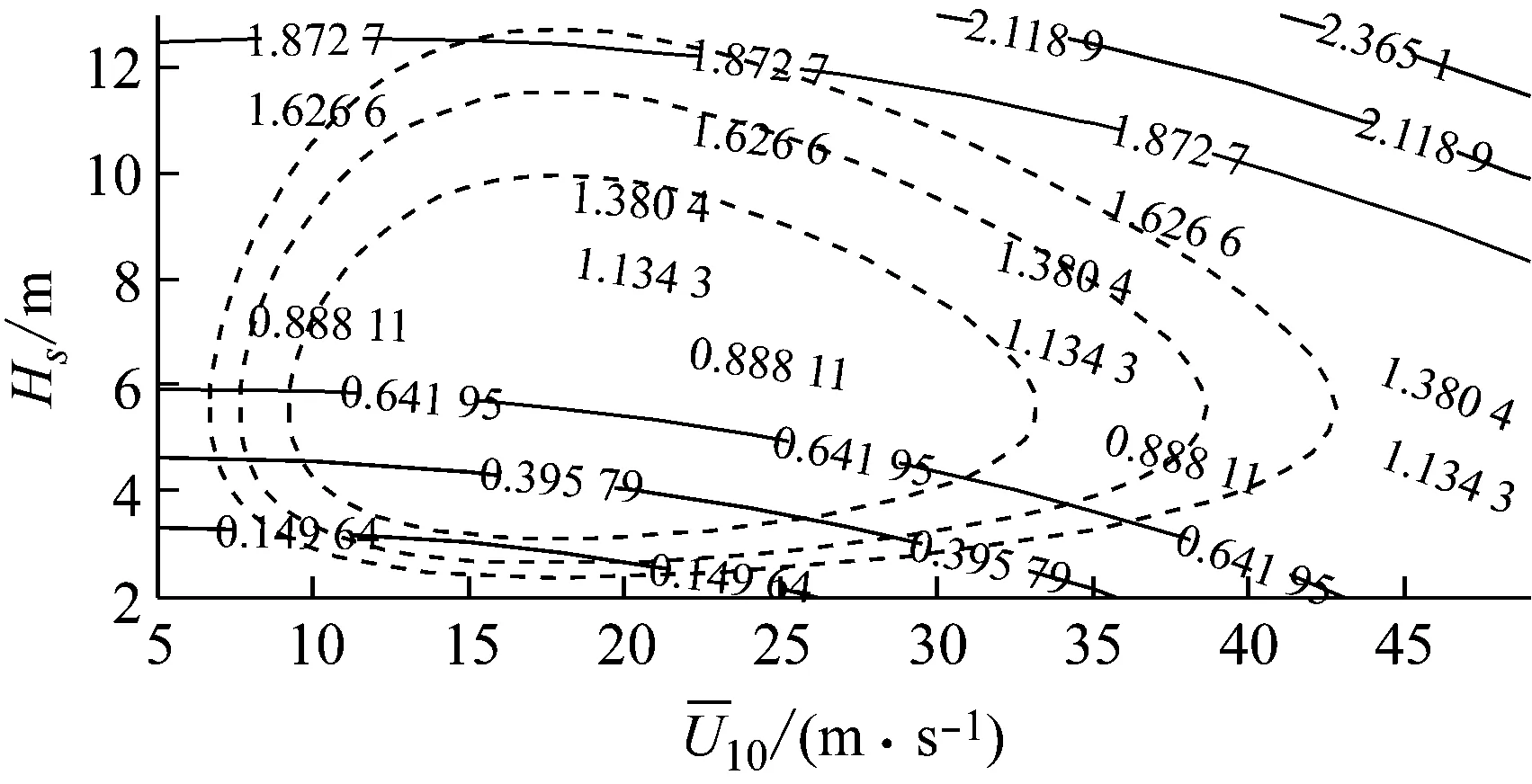
(a) 子樣2-N

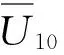
表8為各重現期下基于子樣2、外推法和EC法的橋塔-基礎體系基底剪力極限荷載效應lT，各符號的意義與表7相同。對表8進行分析可得到與表7類似的結論，不再贅述。對于子樣1、子樣2，極限荷載效應lT的計算結果并不相同。在實際工程中為了保證結構安全，應選擇兩者中較大的極限荷載效應進行結構設計。

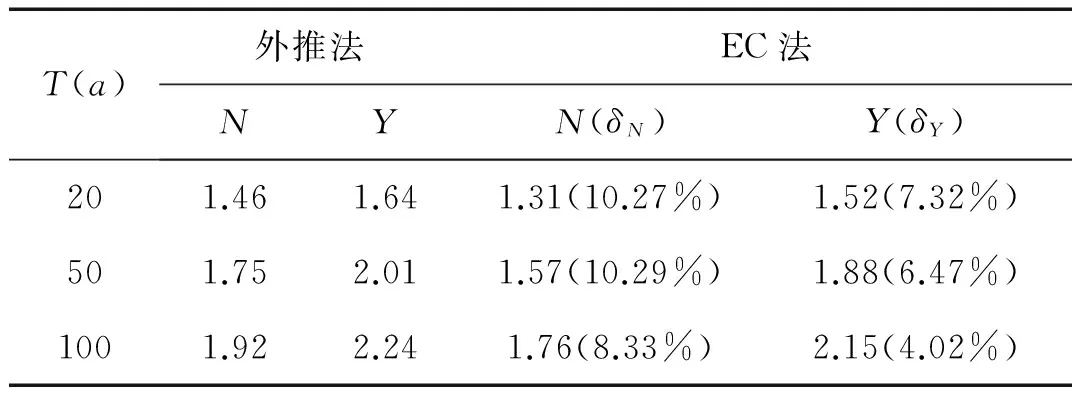
表7 子樣1的極限荷載效應lTTab.7 Extreme load effects lT for subsample 1 ×105 kN

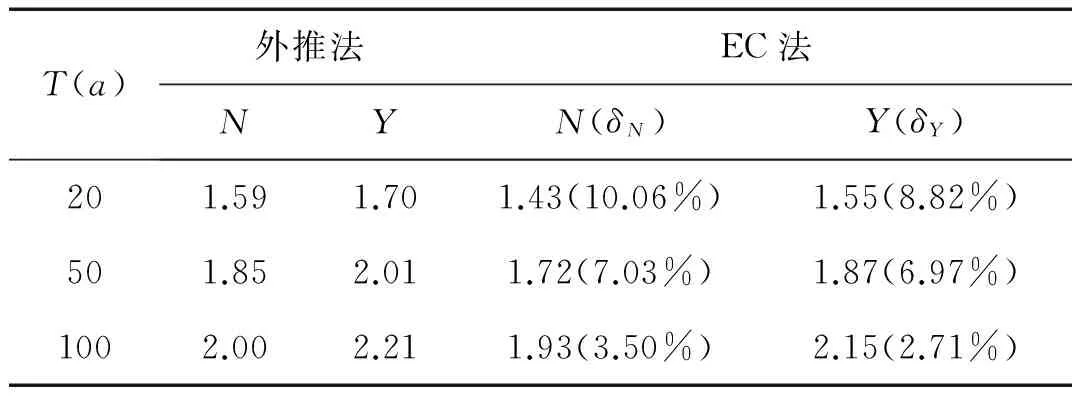
表8 子樣2的極限荷載效應lTTab.8 Extreme load effects lT for subsample 2 ×105 kN

5 結 論

針對基于Rosenblatt映射變換的極限狀態曲線計算困難的現狀，本文提出了極限狀態曲線的簡化算法，提高了EC法的可行性。根據簡化算法和EC法完成了某跨海大橋橋塔-基礎體系基底剪力極限荷載效應估計，并與外推法的計算結果進行了對比，得到了以下結論：

(1) 簡化算法能有效的估計風浪的極限狀態曲線；是否考慮風浪相關性對極限狀態曲線有顯著影響。

(2) 忽略風浪相關性使極限荷載效應的估計值偏小。

(3) 與外推法相比，EC法的計算效率顯著提高。EC法的計算效率與極限狀態曲線離散點的設置有關。為進一步提高EC法的計算效率，極限狀態曲線的離散點可僅設置在使結構荷載效應較大的區域。

(4) 基于EC法的極限荷載效應略小于基于外推法的極限荷載效應，誤差出現的原因是忽略荷載效應極值的變異性。為降低荷載效應極值的變異性，進一步減小基于EC法的極限荷載效應的估計誤差，可適當提高統計樣本的提取閾值。由于估計誤差較小，基于EC法的極限荷載效應可直接用于工程結構設計。

[1] Design of offshore wind turbine structure: DNY-OS-J101[S]. Oslo: Det Norske Veritas, 2010: 9-22.

[2] Wind turbines-Part 1: design requirements: IEC 61400-1[S]. Geneva: Electrotechnical Commission, 2005: 19-32.

[3] 李鋒. 海洋工程雙變量環境條件設計參數估計[D]. 青島:中國海洋大學, 2005:17-40.

[4] 周道成, 段忠東. 耿貝爾邏輯模型在極值風速和有效波高聯合概率分布中的應用[J]. 海洋工程, 2003, 21(2): 45-51.

ZHOU Daocheng, DUAN Zhongdong. The Gumbel-logistic model for joint probability distribution of extreme-value wind speeds and effective wave heights [J]. The Ocean Engineering, 2003, 21(2): 45-51.

[5] 歐進萍, 肖儀清, 段忠東, 等. 基于風浪聯合概率模型的海洋平臺結構系統可靠度分析[J]. 海洋工程, 2003, 21(4): 1-7.

OU Jinping, XIAO Yiqing, DUAN Zhongdong, et al. Structual system reliability analysis for offshore platforms based on the joint probabilistic model of wind and wave[J]. The Ocean Engineering, 2003, 21(4): 1-7.

[6] YUE S. The Gumbel logistic model for representing a multivariate storm event [J]. Advance in Water Resources, 2001, 24(2): 179-185.

[7] 劉偉. 基于最大熵分布的海洋平臺環境條件聯合重現值推算[D]. 青島: 中國海洋大學, 2011: 64-87.

[8] GENES C, FAVRE A C. Everything you wanted to know about Copula modeling but were afraid to ask [J]. Journal of Hydrologic Engineering, 2007, 12(4):347-368.

[9] WIST H T, MYRHAUG D, RUE H. Statistical properties of successive wave heights ans successive wave periods [J]. Applied Ocean Research, 2005, 26(3/4): 114-136.

[10] SILVA-GONZLEZ F, HEREDIA-ZAVONI E, MONTES-ITURRIZAGA R. Development of environmental contours using Nataf distribution model [J]. Ocean Engineering, 2013, 58:27-34.

[11] 陶山山. 多維最大熵模型及其在海岸及海洋工程中的應用[D]. 青島:中國海洋大學, 2013: 76-113.

[12] 董勝, 翟金金, 陶山山. 基于Archimedean Copula函數的風浪聯合統計分析[J]. 中國海洋大學學報, 2014, 44(10): 134-141.

DONG Sheng, ZHAI Jinjin, TAO Shanshan. The joint statistical analysis of wind and wave based on Archimedean Copula functions [J]. Periodical of Ocean University of China, 2014, 44(10): 134-141.

[13] 陳子燊. 波高與風速聯合概率分布研究[J]. 海洋通報, 2011, 30(2): 158-163.

CHEN Zishen. Study on joint probability distribution of wave height and wind velocity[J]. Marine Science Bulletin, 2011, 30(2): 158-163.

[14] YANG X C, ZHANG Q H. Joint probability distribution of winds and waves from wave simulation of 20 years (1989-2008) in Bohai Bay [J]. Water Science and Engineering, 2013, 6(3): 296-307.

[15] ZHANG Y, BEER M, QUEK S T. Long-term performance assessment and design of offshore structures [J]. Computers and Structures, 2015, 154:101-115.

[16] Wind turbines-Part 3: design requirements for offshore wind turbines: IEC 61400-3[S]. [S.l.]: Electrotechnical Commission, TC88 WG3 Committee Draft, 2005: 18-21.

[17] WINTERSTEIN S R, UDE T C, CORNELL C A,et al. Environmental parameters for extreme response: inverse FORM with omission factors: ICOSSAR-93[R]. Innsbruck: [s.n.], 1993.

[18] WINTERSTEIN S R, ENGEBRETSEN K. Reliability-based prediction of design loads and responses for floating ocean structures [C]∥Appeared, Proceedings, 17th Intl. Conf. on Offshore Mechanics and Arctic Engineering. Lisbon: OMAR, 1998.

[19] HAVER S, WINTERSTEIN S R. Environmental contour lines: a method for estimating long term extremes by a short term analysis[C]∥ Transactions-Society of Naval Architects and Marine Engineers.[S.l.]:[s.n.], 2008: 116.

[20] SARANYASOONTORN K, MANUEL L. Design loads for wind turbines using the environmental contour method [J]. Journal of Solar Energy Engineering, 2006, 128(4):554-561.

[21] AGARWAL P, MANUEL L. Simulation of offshore wind turbine response for long-term extreme load prediction[J]. Engineering Structures, 2009, 31(10):2236-2246.

[22] HUSEBY A B, VANEM E, NATVIG B. A new approach to environmental contours for ocean engineering applications based on direct Monte Carlo simulations[J]. Ocean Engineering, 2013, 60(60):124-135.

[23] HUSEBY A B, VANEM E, NATVIG B. Alternative environmental contours for structural reliability analysis[J]. Structural Safety, 2015, 54:32-45.

[24] MONTES-ITURRIZAGA R, HEREDIA-ZAVONI E. Environmental contours using copulas[J]. Applied Ocean Research, 2015, 52:125-139.

[25] GHORBEL A, TRABELSI A. Energy portfolio risk management using time-varying extreme value copula methods[J]. Economic Modelling, 2014, 38: 470-485.

[26] TRIVEDI P K, ZIMMER D M. Copula modeling: an introduction for practitioners. Foundations and Trends in Econometrics [M]. [S.l.]: Now Publishers, 2007: 53-70.

[27] SUNDARESAN A, VARSHNEY P K. Location estimation of a random signal source based on correlated sensor observations[J]. Signal Processing, IEEE Transactions on, 2011, 59(2): 787-799.

[28] RAGAN P, MANUEL L. Statistical extrapolation methods for estimating wind turbine extreme loads[J]. Journal of Solar Energy Engineering, 2008, 130(3): 1-19.

[29] TURKSTRA C J, MADSEN H O. Load combinations in condified structural design [J]. Journal of the Structural Division, 1980, 106(12): 2527-2543.

[30] YEO D. Multiple points-in-time estimation of peak wind effects on structures [J]. Journal of Structural Engineering, 2013, 139(3): 462-471.

[31] MYRHAUG D, ONG M C. Effect of wave age on wind gust spectra over wind waves[J]. Journal of Offshore Mechanics and Arctic Engineering, 2009, 131(3): 034501.

[32] Environmental conditions and environmental loads Recommended Practice: DNV-RP-C205[S]. [S.l.]: DNV, 2012.

[33] 涂志斌, 黃銘楓, 樓文娟. 風浪耦合作用下橋塔-基礎體系的極限荷載效應[J]. 浙江大學學報(工學版), 2016, 50(4): 601-610.

TU Zhibin, HUANG Mingfeng, LOU Wenjuan. Extreme load effects on a bridge tower-basement system due to the joint actions of wind and wave [J]. Journal of Zhejinag University (Engineering Science), 2016, 50(4): 601-610.

Extremeloadeffectsonabridgetower-basementsystemunderthejointactionofwindandwavebasedontheECmethod

TU Zhibin，HUANG Mingfeng，LOU Wenjuan

(Institute of Structural Engineering, Zhejiang University, Hangzhou 310058, China)

A simplified algorithm was developed to construct the limit state line of multi random variables, aiming at overcoming the difficulty in the construction of limit state line by Rosenblatt transformation. By searching the expected values of variables which can satisfy the marginal distributions, joint cumulative distribution and reliability index simultaneously, the calculation of conditional distribution function and its inverse function was turned to find the inverse function of marginal distribution, and thus the construction of the limit state line was simplified. Taking some bridge tower-basement system as an engineering example and the wind-wave simultaneous observation data at the Weizhou marine station as statistic samples, the joint cumulative distribution function of wind and wave was estimated by an Copula function, the limit state line of wind and wave was constructed by the proposed algorithm, and the extreme load effects of the base shear force were estimated by the environmenlal contour (EC) method and compared with those estimated by a statistical extrapolation method. It is demonstrated that the extreme load effects estimated by the EC method together with the simplified algorithm is highly accurate.

extreme load effect; limit state line; joint action of wind and wave; environmental contour method; copula function

TU411; TU472.5

A

10.13465/j.cnki.jvs.2017.19.019

交通運輸部科技項目(2011318223170);國家自然科學基金資助項目(51578504)

2016-04-19 修改稿收到日期：2016-08-04

涂志斌 女，博士生，1988年9月生

黃銘楓 男，博士,副教授，博士生導師,1976年10月生