基于模值估計的三軸磁力計標定方法研究*

鐘 浩,章衛國,劉小雄

(西北工業大學自動化學院,西安 710129)

項目來源:國家自然科學基金項目(61374032);航空科學基金項目(20150753009)

2017-04-13修改日期2017-06-07

基于模值估計的三軸磁力計標定方法研究*

鐘 浩,章衛國*,劉小雄

(西北工業大學自動化學院,西安 710129)

現有的三軸磁力計標定方法大都是對采樣數據進行歸一化,然后利用樣本數據求解參數。為了提高標定算法的通用性和有效性。提出了一種改進的標定方法,首先將磁力計所處位置磁場向量的模作為誤差模型參數,然后對其進行估計算法設計,接著提出一種兩步標定方法進行參數初值的選取,然后應用Levenberg-Marquardt方法進行磁力計標定算法設計。仿真和實驗結果表明,本文所提算法對類似的三軸傳感器具有通用性,不依賴于傳感器的觀測向量,同時能夠對所觀測向量的模值進行精確的估計,可以標定三軸磁力計的安裝誤差、靜態靈敏度誤差和零位誤差,標定過程簡便,適用性廣。

三軸磁力計;誤差分析;兩步標定方法;Levenberg-Marquardt方法

磁力計是通過測量地磁場強度來指示方向的設備,其輸出具有連續性、誤差不積累等特性[1]。在低成本高性能的導航系統中,磁力計是用于姿態估計的關鍵性輔助傳感器[2],因此廣泛應用于低成本飛行器的組合導航系統中。這種低成本、低功耗傳感器通過比較機體系和導航系的磁場強度來給出相對精確的航向[3]。

由于制造、安裝以及環境等因素的影響,實際使用中,三軸磁力計都會存在著未對準、靈敏度不一致和零偏等誤差,導致測量值誤差過大[4-6],因此必須對三軸磁力計進行標定之后,才能將三軸磁力計用于組合導航系統中。本文通過建立三軸磁力計的數學模型,使用兩步標定方法求解模型參數。通過仿真和實驗結果表明所改進的算法的有效性。

1 誤差分析及模型建立

根據傳感器誤差產生機理的不同,可將三軸磁力計的誤差分為安裝誤差、靈敏度不匹配誤差和零位誤差。

1.1 安裝誤差

安裝誤差也叫未對準誤差,是由于在運載體上以捷聯方式安裝三軸磁力計時,磁力計的3個測量軸分別與載體的3個軸不平行而引起的測量誤差[7]。理想的三軸磁力計相對于載體坐標系的安裝誤差表示為三軸磁力計依次繞Z軸、Y軸和X軸轉動3個微小的安裝角。根據兩坐標系之間的轉換矩陣,和安裝誤差的小角度特性,可以得到安裝誤差的數學模型:

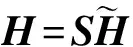
(1)

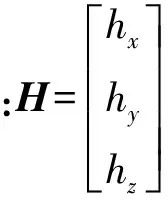
1.2 三軸間靜態靈敏度不匹配誤差

實際應用中一般使用三軸磁力計,用來測量磁場在3個軸上的投影分量。磁力計的三軸的測量特性總會存在一些差異,因此造成三軸間靜態靈敏度不匹配誤差。一般三軸的靜態靈敏度均趨近于1,因此三軸間靜態靈敏度不匹配誤差的數學模型為:

(2)

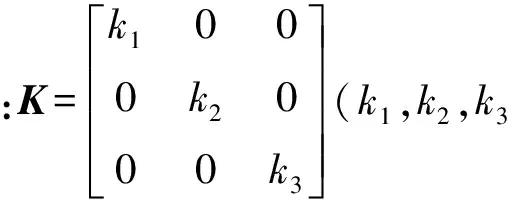
1.3 三軸磁力計的零位誤差

零位誤差又稱為零偏誤差[7],是由于傳感器、模擬電路和A/D轉換的零點不為零以及數據處理過程中數據偏移所引起的誤差。此外硬磁干擾誤差是一種常值干擾誤差,其值一般不隨時間而發生變化,因此一般也可等效為三軸磁力計的零位誤差[8-9]。三軸磁力計的零位誤差的數學模型為:

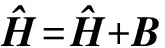
(3)

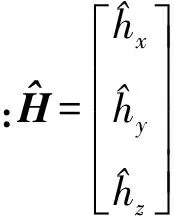
1.4 三軸磁力計標定的完整數學模型

為了在工程上應用的方便性,以及降低對校準條件的要求,本文忽略了由于三軸磁力計軸間非正交而產生的誤差以及由于軟磁干擾而產生的誤差以及其他干擾很小可以忽略的誤差。由式(1)～式(3)可得三軸磁力計標定的完整數學模型為:

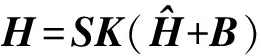
(4)

式中:H也就是標定后的載體坐標系上的磁場向量的投影。

2 傳感器標定算法設計

2.1 模型分析

在三軸磁力計軸間靜態靈敏度不匹配誤差模型中,三軸靈敏度都趨近于1。為了可以得到磁場向量的模大小,本文以三軸中的Z軸的靜態靈敏度作為基準,X和Y軸的靈敏度都是相對于Z軸的比值。

這樣會帶來一些新的問題:也就是真實的磁場向量的模與本文所得到的磁場向量的模之間會有一個Z軸靜態靈敏度的系數倍數偏差,三軸真實的靜態靈敏度系數也會與本文所得到得靜態靈敏度系數有一個Z軸靜態靈敏度系數的偏差。不過由于Z軸靜態靈敏度系數本身趨近于1,而且在使用三軸磁力計測量值計算方向角時是兩軸之間測量值的比值,因此并不會使計算出的方向角產生誤差。

如果不以Z軸靜態靈敏度系數作為基準,會造成計算出的磁場向量長度,以及三軸靈敏度之間存在一個倍數關系,在使用Levenberg-Marquardt方法求解模型參數最優解時會出現靈敏度系數和向量模與真實值之間偏差一個倍數關系,而這個倍數關系可大可小,會帶來估計上的不準確性。

2.2 算法設計

根據上述分析和標定模型,進一步分析如下,對式(4)有:

(5)

進一步有:

(6)

為了簡化算法分析過程,本文將式進一步寫為:

(7)

即

當三軸磁力計在一固定地理位置作各種姿態變化時,可以將磁場向量視為常向量,其磁場向量的模為一常數。因此對于式(7)有:

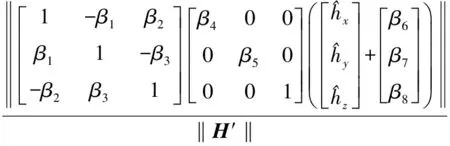
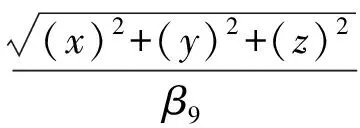
(8)

式中:

通過采集多組數據,使用最小二乘法擬合的方法,本文中的優化目標函數為:

(9)

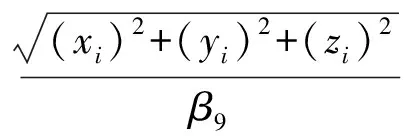
由于ri(β)是非線性的,故式(9)所表示的目標函數的極小點通常稱為非線性最小二乘問題。由于Levenberg-Marquardt型方法是求解這類問題的最有效方法之一,特別是對于殘差為零或接近于零的問題[10]。因此本文采用此方法對此非線性最小二乘問題進行求解。

2.3 算法第1步:初值求解

由于本文中的模型一共有9個參數需要確定,而且各個參數值得范圍以及大小都是不同的。而且由于Levenberg-Marquardt型方法的收斂性問題,在初值的選擇上不能偏離真實值太多,否則會造成難以收斂、收斂時間較長或者收斂到其他局部最優解[11]。其中可以確定的是β1,β2,β3為趨近于0的數值,β4,β5趨近于1的數值。但是由于不同的傳感器測量的物理量的不同,造成物理量的模β9的大小難以確定具體的范圍。而且即使在同一類型的傳感器下,由于設置的增測量范圍不同,傳感器AD采樣的輸出數值范圍也是不一樣的。因此在使用Levenberg-Marquardt型方法時難以確定具體的參數β9的大小。對于參數β6,β7,β8也具有同樣的結果。因此在使用Levenberg-Marquardt型方法對目標函數進行求解時需要先確定的參數β6,β7,β8,β9的適當范圍。

本文中先忽略其他誤差因素,認為β1,β2,β3,β4,β5均為理想值。因此式(4)可以寫為:

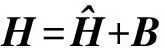
(10)

進一步有:

(11)

也就是:

對于樣本數據有:

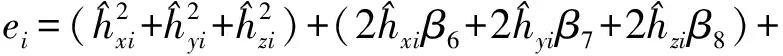
(12)

對于n個樣本數據有:

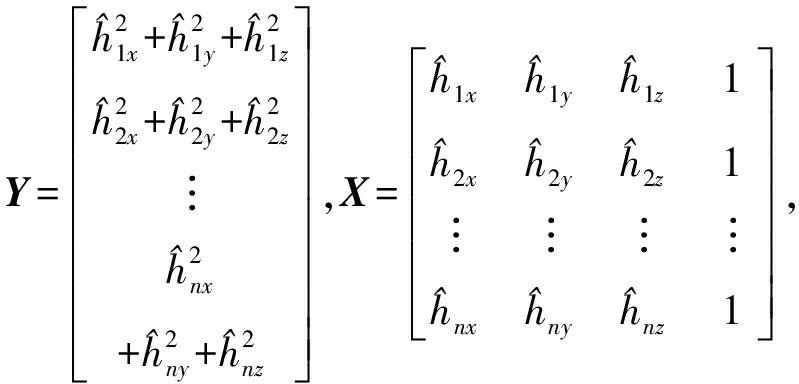
(13)

通過解算式(13)的結果,可以得到參數β6、β7、β8、β9的值,本文將該值作為第2步求解的初始值對目標函數進行求解。

2.4 算法第2步:非線性最小二乘求解

針對優化目標函數式(9),使用Levenberg-Marquardt方法進行求解[10]。該方法的主要計算公式為:

(JTJ+μI)β=-g

(14)

式中:J為r(β)函數的雅克比矩陣,g=?f/?β為優化目標函數的梯度,μ≥0為阻尼因子,I為單位陣,β為參數變量的變化值。下次迭代計算是βk+1=βk+β。

3 實驗結果與分析

3.1 數值仿真部分

取磁場向量模為10,安裝誤差角度為5°,三軸靜態靈敏度系數分別為0.98,1.02,0.96,三軸零位誤差分別為-3,-3,-3,噪聲均值為0,方差為0.01。產生原始的樣本數據,利用本文提出的算法進去求解。

解算模型參數如表1所示。從解算的參數可以看出,在其他參數基本一致的情況下,第2步解算明顯提高了第1步解算的向量的模值精度。

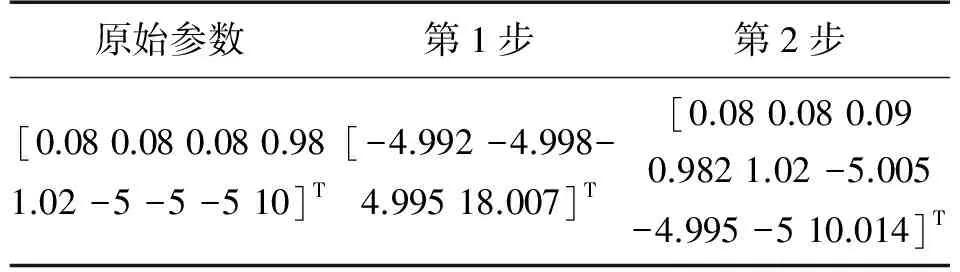
表1 仿真參數對比

標準差能夠從向量模的大小來反映參數的優劣程度。當標準差越小,說明標定后的向量模越趨近于一個常值,這與磁場向量在一固定地理位置具有固定的模是吻合的,也就是說標準差越小,參數和真實的參數越接近。表2中的數據也表明了標定的有效性。

表2 仿真向量模標準差對比

圖2為標定前后數據圖形對比。在同樣的仿真數據環境下,當不使用文中的最小二乘法來計算參數的初值時,選取參數的初值為[0.001,0.001,0.001,1,1,1,1,1,1]T,可以得到仿真結果為:[7.519,1.049,0.7147,0.163,0.143,23.448,57.858,36.92,50.567]T。圖1為未使用最小二乘法計算初值的仿真圖形,可以明顯看出解算結果偏離理想結果。

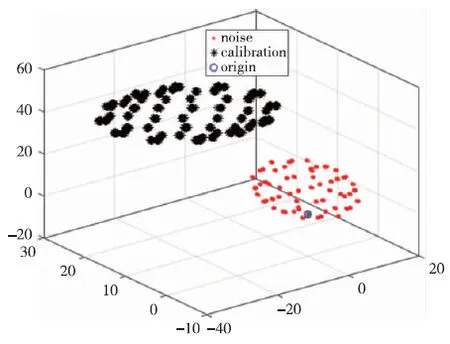
圖1 仿真數據標定前后對比圖

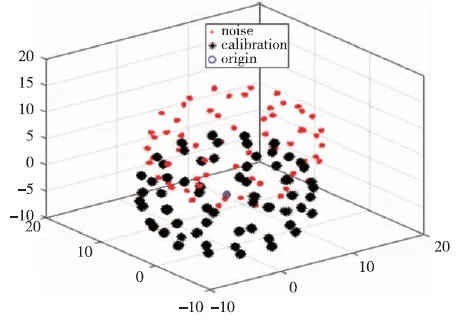
圖2 仿真數據標定前后對比圖

3.2 實驗數據分析

對于三軸的傳感器一般都具有相似的誤差源,因此本文所建立的模型具有一定的通用性[12]。首先利用三軸加速計的輸出,測試模型的效果。

3.2.1 三軸加速度計

通常認為重力加速度的值是固定的,一般為9.8 m/s2。因此將模型解算的參考向量和該值進行對比可以說明對向量模估計值得精確度。

采樣數據來源為MPU6050。MPU6050模塊是InvenSense公司推出的一款低成本的6軸傳感器模塊,包括三軸加速度,其體積小巧,用途非常廣。采集多種姿態下,加速度計的輸出,共145組樣本數據。表3為經過算法標定后的標定參數。表4為數據向量的標準差比較。

表3 三軸加速度計真實參數解算

表4 重力加速度標準差比較

從表中可以看出第1步只能給出偏差較大的參數初值,第2步會在該初值的基礎上得到進一步優化的結果。

通過10.043/9.8=1.024 8可知,Z軸的靜態靈敏度系數最大不過1.024 8,與估計的X軸靜態靈敏度系數1.017和Z軸靜態靈敏度系數1.018比較接近。

圖3為標定前后數據圖形對比。

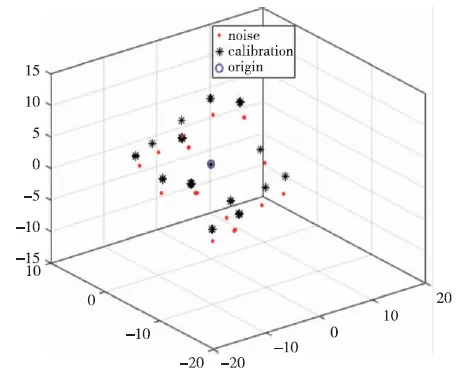
圖3 三軸加速度計標定前后對比圖

3.3 三軸磁力計

本文從HMC5883L三軸磁力計采集數據。HMC5883L是霍尼韋爾公司生產的帶有數字接口的弱磁傳感器芯片。在空間中隨意轉動三軸磁力計,采集三軸磁力計的輸出。表5為經過算法標定之后的參數,其中向量模為傳感器輸出的ADC值。將表3和表5對比可知,由于重力向量和磁場向量的不同,參數的范圍差別比較大。在選取參數的初值時,無法確定參數的具體范圍,因為不同的觀測向量模差別比較大。從而表明了兩步法的有效性。

表5 三軸磁力計真實參數解算

表6為標定前后數據向量模標準差大小。

表6 磁場向量模標準差比較

圖4為標定圖形。

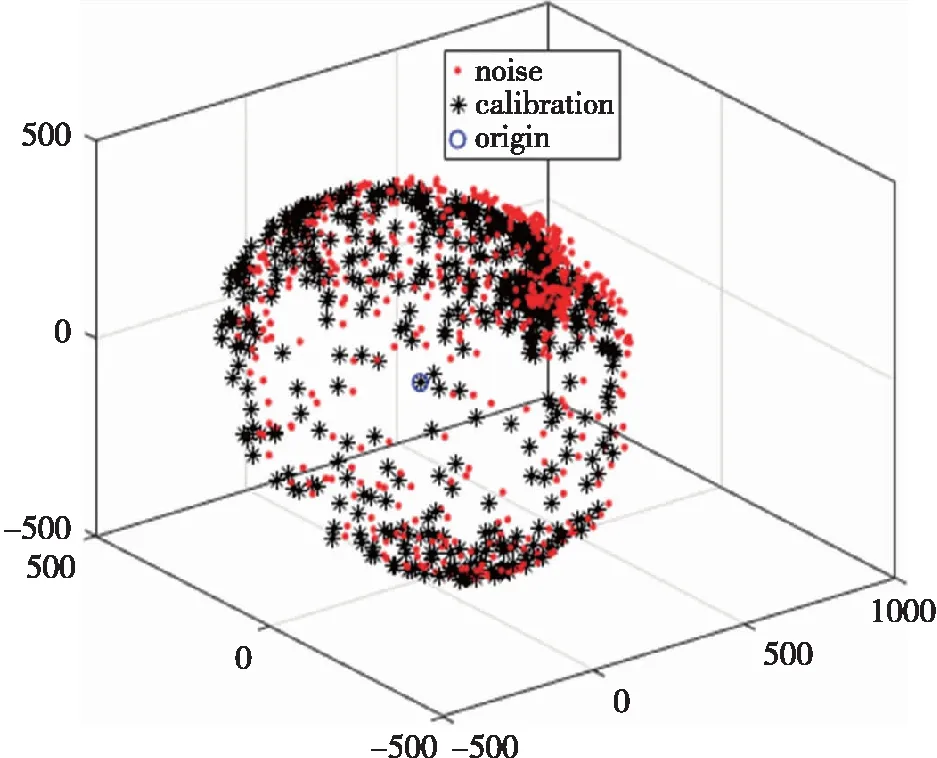
圖4 三軸磁力計標定前后數據對比

將表3和表5對比可知,由于重力向量和磁場向量的不同,參數的范圍差別比較大。在選取參數的初值時,無法確定參數的具體范圍,因為不同的觀測向量模差別比較大。從而表明了兩步法的有效性。

4 總結

考慮現有的三軸磁力計的標定方法大部分是對三軸磁力計的采樣數據進行歸一化處理,然后利用歸一化的樣本數據對三軸磁力計模型的參數進行求解,沒有將所處位置的磁場向量模作為模型參數,因而在模型中忽略了磁場向量的模。本文提出了一種改進的三軸傳感器的標定方法。構建標定模型的非線性最小二乘算法模型,采用兩步解算方法進行參數的結算,先確定出參數的大致范圍,然后使用Levenberg-Marquardt方法對目標函數進行求解。通過仿真和實驗結果表明該方法能夠提高算法的收斂性和通用性,并且具有較廣泛的工程應用價值。

[1] Fang J,Sun H,Cao J,et al. A Novel Calibration Method of Magnetic Compass Based on Ellipsoid Fitting[J]. IEEE Transactions on Instrumentation and Measurement,2011,60(6):2053-2061.

[2] Vasconcelos J. A Geometric Approach to Strapdown Magnetometer Calibration in Sensor Frame[C]//Navigation,Guidance and Control of Underwater Vehicles,2008:172-177.

[3] Markley F L. Attitude Determination and Parameter Estimation Using Vector Observations:Theoty[J]. The Journal of the Astronautical Sciences,1989,37(1):41-58.

[4] 張煒,程錦房. 一種三軸磁傳感器正交誤差校正的簡便方法[J]. 兵工自動化,2009(12):75-78.

[5] 范成葉,李杰,陳文蓉,等. 電子羅盤安裝誤差標定與補償方法研究[J]. 傳感技術學報,2013,23(5):622-626.

[6] 邱秀分,石文峰,孫春艷,等. 一種高精度的小型三維電子羅盤簡易標定方法[J]. 艦船電子工程,2017(2):82-85,125.

[7] 張曉明. 地磁導航理論與實踐[M]. 北京:國防工業出版社,2016:75,79,112.

[8] Gebreegziabher D,Elkaim G H,Powell J D,et al. Calibration of Strapdown Magnetometers in Magnetic Field Domain[J]. Journal of Aerospace Engineering,2006,19(2):87-102.

[9] Valérie R,Afzal M H,Gérard L. Complete Triaxis Magnetometer Calibration in the Magnetic Domain[J]. Journal of Sensors,2010,2010(1):23-59.

[10] 梅芳,張建中. Levenberg-Marquardt型非線性最小二乘算法的收斂性[J]. 計算數學,1982(2):182-192.

[11] 張春曉. 解決非線性最小二乘問題的兩種方法[J]. 青海大學學報(自然科學版),2003(5):60-64.

[12] Foster C C,Elkaim G H. Extension of a Two-Step Calibration Methodology to Include Nonorthogonal Sensor Axes[J]. IEEE Transactions on Aerospace and Electronic Systems,2008,44(3):1070-1078.

ResearchonCalibrationMethodsofThree-AxisMagnetometerBasedonVectorNormEstimation*

ZHONGHao,ZHANGWeiguo*,LIUXiaoxiong

(College of Automation,Northwestern Polytechnical University,Xi’an 710129,China)

In view of calibration methods of three-axis magnetometer,most calibration methodsuse the normalized magnetic field vector to calibrate three-axis magnetometer. In order to improve the generality and effectiveness of calibration methods,a two-step calibration method is proposed. In this work,the error model of three-axis magnetometer uses the magnetic field vector norm as a parameter. First step is used to get the initial parameters,then second step is used to solve nonlinear least squares problem with the initial parameters. Simulation results show that two-step calibration method can improve the convergence of Levenberg-Marquardt method. This method does not depend on the observed vector,and is also applicable to other three-axis sensors with the same error model. And experiment results show that this method can correctly and effectively compensate the misalignment errors,null shift errors and sensitivity errors of the three-axis magnetometer. And the magnetic field vector norm is relatively precise.

three-axis magnetometer;error analysis;two-step calibration method;Levenberg-Marquardt method

V241.61

A

1004-1699(2017)10-0512-06

10.3969/j.issn.1004-1699.2017.10.010

鐘浩(1991-),男,西北工業大學自動化學院碩士研究生,研究方向為旋翼機組合導航算法,zhonghao@mail.nwpu.edu.cn;

章衛國(1956-),男,教授,西北工業大學博士生導師,研究方向為飛行控制與仿真、現代飛行控制方法;

劉小雄(1973-),男,博士,西北工業大學副教授,研究方向為飛行控制與仿真、非線性飛行控制方法、飛行控制系統設計。