基于復合材料的水下耐壓結構拓撲優化探究

戴 揚 ，馮淼林 ，趙 敏 ,2

(1. 上海交通大學 海洋工程國家重點實驗室，上海 200240；2. 高新船舶與深海開發裝備協同創新中心，上海 200240)

基于復合材料的水下耐壓結構拓撲優化探究

戴 揚1，馮淼林1，趙 敏1,2

(1. 上海交通大學 海洋工程國家重點實驗室，上海 200240；2. 高新船舶與深海開發裝備協同創新中心，上海 200240)

探究基于復合材料的拓撲優化設計方法在水下耐壓結構設計中的應用。本文方法是在等值線方法、SIMP（Solid Isotropic Material with Penalization）模型、靈敏度過濾技術的基礎上，推導復合材料的等效剛度矩陣。通過經典橋形結構優化算例、靜水壓作用下的結構拓撲優化設計以及空心水下耐壓結構優化設計，分析了在拓撲相關載荷作用下，復合材料對于水下耐壓結構的最優拓撲形式的影響。發現復合材料與各向同性材料結構的優化結果比較相似，而復合材料的鋪層方式及角度的變化可能對優化結果產生較大的影響，本文對空心耐壓結構的優化結果與MIT 團隊提出的耐壓殼概念相類似，說明復合材料的拓撲優化研究對于未來水下耐壓結構的設計具有重要的參考價值及指導意義。

耐壓結構；拓撲優化；復合材料；拓撲相關載荷

通過陶瓷材料在 11 000 m“海神”號深潛器的應用可以發現，復合材料的使用造成了水下耐壓結構的巨大改變，而為了能探究復合材料究竟對于耐壓結構的設計產生如何的影響，就需要一種方法能夠計算基于復合材料的結構設計模型。采用拓撲優化方法，能夠直觀地模擬材料的最優分布，對于探尋基于復合材料的耐壓結構最優拓撲形式有著重要的參考意義。

1 復合材料拓撲優化設計

拓撲優化最開始產生于 20 世紀初的 Michell 桁架[2]的設計中，之后在 1988 年 Bendsoe 與 Kikuchi[3]在連續結構設計中提出均勻化方法后得到了快速發展，并且延伸到諸多其他學科領域中。在拓撲優化的方法中，均勻化方法和變密度法[3–7]作為最具代表性的方法被廣泛地應用，而在兩者之中，變密度法由于其插值模型在算法上更易實現，是更具有工程應用前景的一種拓撲優化方法。密度法插值模型的基礎是由 Mlejnek 與Schirrmacher[8]提出的一種對結構材料密度的冪次懲罰模型，他們通過在 0 – 1 的離散結構優化問題中引入連續設計變量，并加入中間密度的懲罰項，將問題轉變為連續結構優化問題。之后，Sigmund 與 Bendsoe[9–10]提出了一種基于正交各向同性材料的密度冪指數形式的變密度插值方法（SIMP），它將單元密度與材料的彈性模量之間建立起聯系，從而減少了設計變量，簡化了優化過程。雖然拓撲優化方法已經被應用在了很多工程設計中，但其中很少有關于拓撲相關載荷的優化。與固定載荷的優化問題不同，在拓撲相關載荷的優化設計中，載荷的方向與位置處于隨著結構邊界變化而改變，如何確定拓撲相關載荷作用的加載面是解決這類問題的關鍵。在 Maute 與 Ramm[11]提出的等值線概念的基礎上，Hammer 與 Olhoff[12]引入了1條等體積密度曲線來作為加載面。而 Du 與 Olhoff[13]提出了一種修正的等值線技術，在其文章中，還討論了載荷靈敏度與周邊單元的關系，并指出單元內的加載面只受到相鄰單元的密度的影響，從而大大減少了靈敏度分析的計算量。在以往的拓撲優化研究中，被優化的結構多是各向同性材料，有關復合材料的拓撲

優化的研究很少。相比于傳統的各向同性材料，復合材料由于其自身的強度高、剛度大等特點，將復合材料用于拓撲優化中，可能會出現未知的特殊效果。而為了能解決基于復合材料的拓撲優化問題，Lee 等[14]修改了拓撲優化中的單元剛度矩陣，以此來適應正交各向異性材料的情況。在拓撲優化過程中，為了避免拓撲優化中出現多孔材料、棋盤格、網格依賴性等數值不穩定的現象，同時保證優化的效果及效率，往往需要用到靈敏度過濾技術。Sigmund 提出了一種距離加權的靈敏度過濾方法，它能有效地消除大部分數值不穩定的現象，但它往往不能得到完全離散的優化結果。為了獲取清晰的邊界，有很多不同的靈敏度過濾公式被引入拓撲優化問題中，包括 Borrvall 提出的修正的靈敏度過濾方法，平均靈敏度過濾方法，考慮密度梯度的靈敏度過濾方法[15–17]等。對于不同的優化問題，能達到最佳過濾效果的方法往往也不會完全相同，因此，在拓撲優化中需要尋找適合的靈敏度過濾方法。本文的研究是基于文獻[14]將 SIMP 模型應用于復合材料拓撲優化的思路，推導復合材料的等效單元剛度矩陣，來實現復合材料的拓撲優化。并且將此方法用于水下耐壓結構的最優拓撲形式的探究中，分析復合材料對于拓撲優化結果的影響。

2 拓撲優化數學模型

本文從最簡單的結構拓撲優化問題開始研究，即在給定體積約束下使得結構具有最小的柔順度。設有給定的設計區域 Ω，將其離散成 N 個有限單元，根據SIMP 模型，對于各向同性材料[18]，每個單元具有相對密度并且可以得到單元的彈性模量:

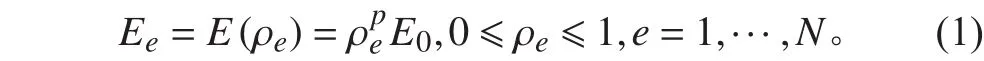
式中：E0為固體材料的彈性模量；p 為懲罰系數，在本文中取為 3。

在這個設計問題中，連續體結構最小柔順度的優化模型為：

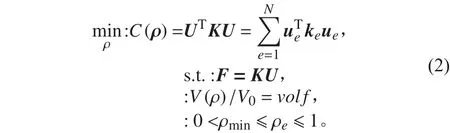
式中：ρ 為單元相對密度構成的矩陣；K，F 和 U 分別為總體剛度矩陣、載荷矩陣和位移矩陣；ue為單元的位移矩陣；為單元的剛度矩陣，且為對應于單位彈性模量的單元剛度矩陣；V(ρ)和 V0分別為優化后結構的體積和初始的設計區域的體積；v olf 為預設的體積分數；是為了避免總體剛度矩陣的奇異性而引入的非零常數，在本文中取為 0.001。

使用 SIMP 模型來求解式（2），原本基于離散變量的設計問題轉化為基于連續變量的優化問題。本文使用等值線方法[12–13]作為邊界搜索方法來尋找拓撲變化相關的壓力加載面，而由于設計變量數目多，采用移動漸近線方法（MMA）[19]來求解更新設計變量。本文采用平均靈敏度過濾方法[16]與考慮密度梯度的敏度過濾方法[17]相結合的靈敏度過濾方法。

3 復合材料的單元剛度矩陣

本文研究基于纖維增強型復合材料層合板的拓撲優化問題，由于復合材料層合板的厚度相較于長寬很小，故可以將其視為平面應力板。坐標系的設定如圖 1 所示，圖中坐標系 1和2 為材料主向坐標系，而坐標系 x – y 為自然坐標系；θ 表示坐標軸 x 與坐標軸1 的夾角，以沿著逆時針方向為正。

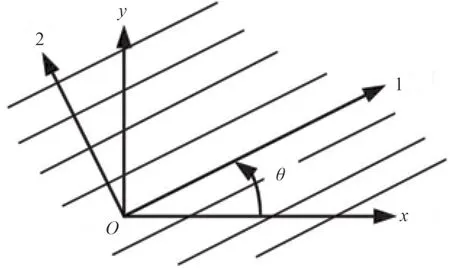
圖1 材料主向坐標系與自然坐標系Fig. 1 Principle coordinate system of material and natural coordinate system

根據材料力學相關知識，則正交各向異性材料的彈性矩陣為：

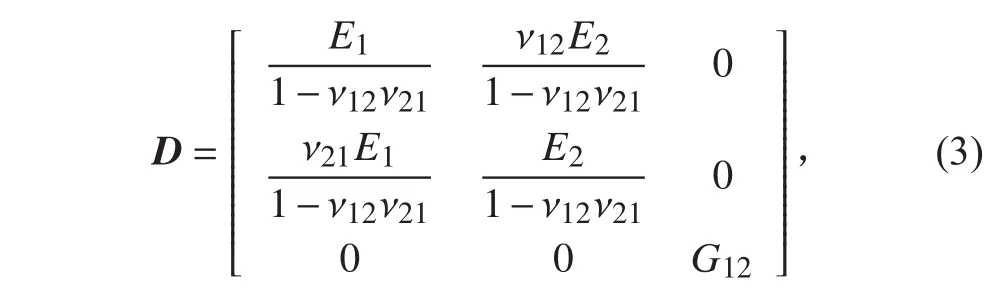
式中：E1和 E2分別為沿著 1 方向和 2 方向的材料彈性模量；v12和 v21為1 方向和 2 方向之間的泊松比；G12為材料主向坐標系下的剪切模量。

式（3）的材料彈性矩陣是在材料主向坐標系下的形式，通過坐標變換，則在自然坐標系下的轉換后的彈性矩陣可記為：

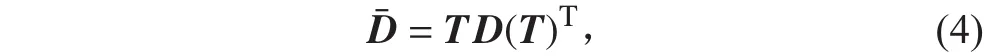
其中T 為坐標變換矩陣，其表達式為：

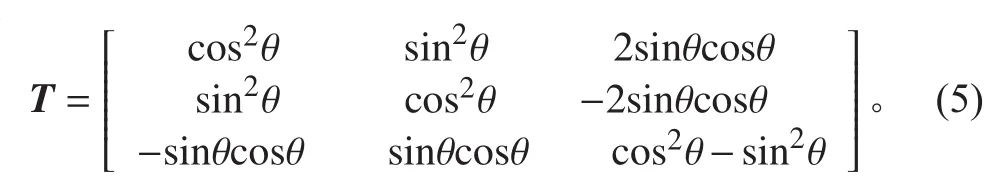
在本文的數值分析中，選擇二維線性等參單元作為基本單元。則為了計算單元內某個點的位移，其計算公式為：

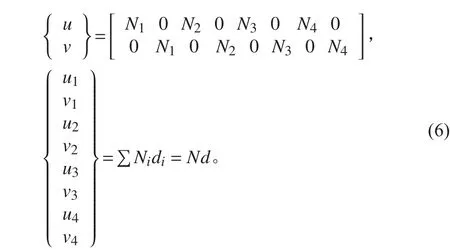
式中：Ni為拉格朗日插值函數，di為單元節點的位移分向量，

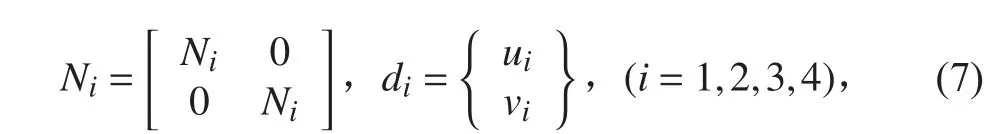
進而自然坐標系下的應變矢量 ε 可表示為：

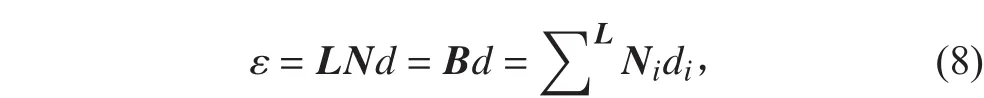
其中：

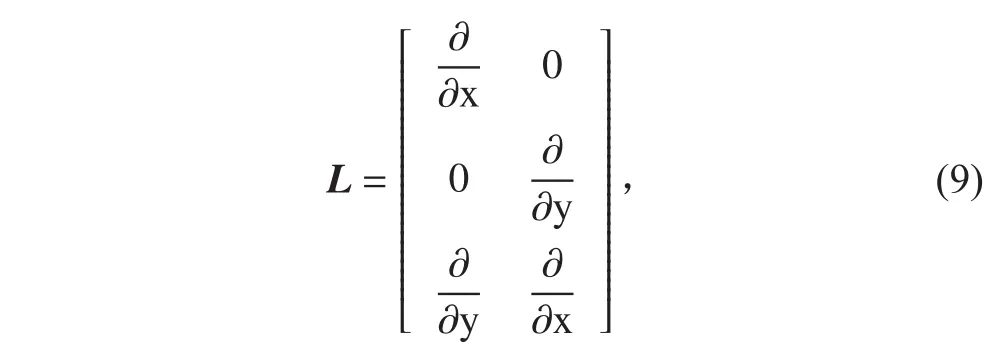
則將自然坐標系下的應力矢量 σ 定義為：

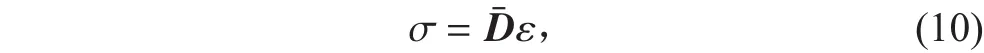
對于彈性材料，單元應變能的表達式可以表示如下：

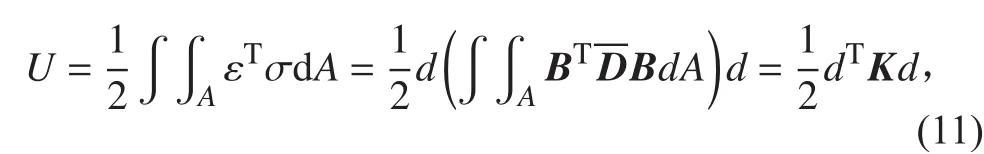
其中：

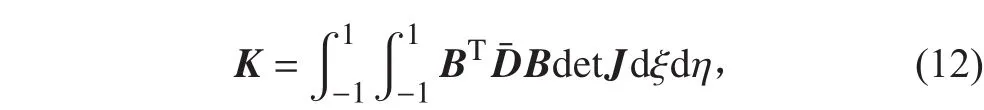
式中J 為雅可比矩陣，其行列式 det J 為：

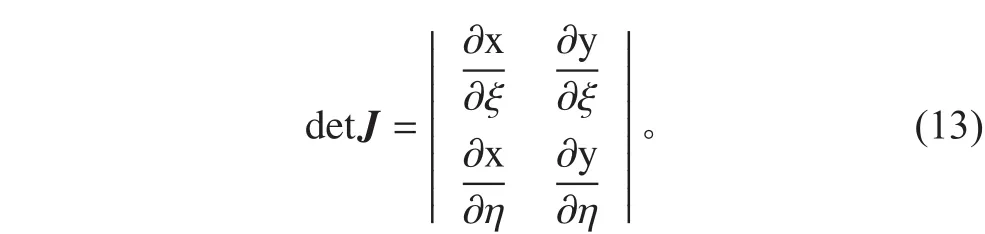
根據復合材料力學，可以推出等效單元剛度矩陣為：

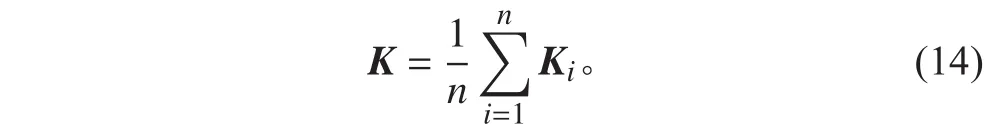
其中：Ki為自然坐標系下第 i 個鋪層的剛度矩陣，可以由式（12）計算得到；n 為層合板的總鋪層數。

4 靈敏度分析

本文采用的 MMA 方法是基于梯度的優化算法，優化問題中的目標函數和約束對設計變量的靈敏度分析不能忽略。Wang 等[20]在其關于距離正規化水平集方法（DRLSE）應用于壓力加載面搜索算法的文章中，提到了相應的靈敏度分析。本文采用的是等值線方法作為壓力加載面搜索算法，因此本文的靈敏度分析與Wang 的方法略有不同。

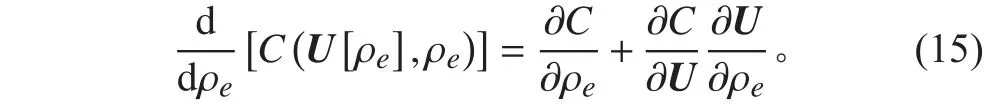
根據平衡方程以及靈敏度關系式，采用伴隨法[21]對進行求解，從而可以將式（15）轉化為[20]：

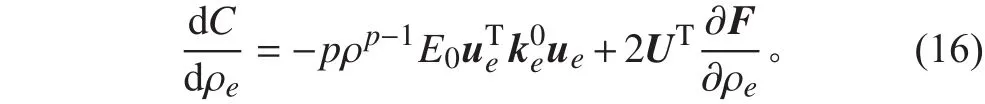
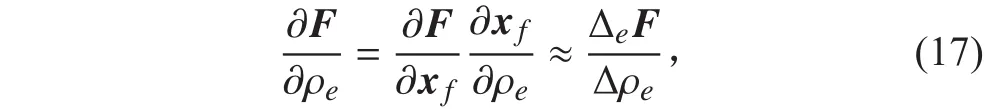
其中：

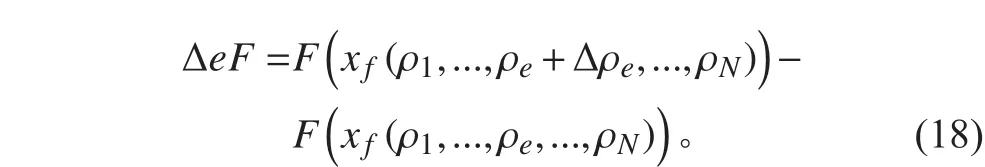
式中：xf為加載面與單元邊界交點的坐標矩陣；為給定的較小的單元相對密度增量（本文中取利用等值線方法計算得到新的加載面與單元邊界交點的坐標矩陣 xf以及對應的載荷矩陣F，代入式（17）中可計算出載荷的靈敏度。

5 數值算例

本文所計算的算例為基于復合材料的拓撲優化問題，所采用的材料為纖維增強型復合材料，其鋪層模型如圖 2 所示。并且根據不同的算例，本文將選用不同的靈敏度過濾技術來獲得更好的優化結果。

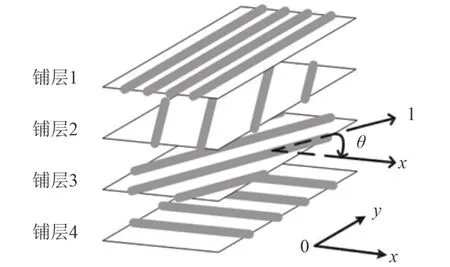
圖2 復合材料鋪層模型Fig. 2 A model laminated with composite material

5.1 外部受壓的橋形結構優化設計

作為承受壓力載荷的結構優化問題中的經典算例，本文選擇外部受壓的橋形結構優化設計作為第一個算例，用以驗證推導的復合材料的單元剛度矩陣的可靠性，并研究復合材料對于拓撲優化結果的影響。初始的設計區域以及邊界約束條件如圖 3（a） 所示，長方形設計區域的長寬分別為 2 m 和 1 m，頂端受到方向垂直向下大小為 2 MPa 的均布壓力載荷的作用，長方形設計區域的底邊 2 個頂點固支。假設材料的彈性模量分別為，，泊松比v12= 0.3，則優化問題變為基于各向同性材料的拓撲優化。設計區域離散成 40 × 20 個正方形單元，且最大允許的材料體積占初始總體積的體積分數為 50%。

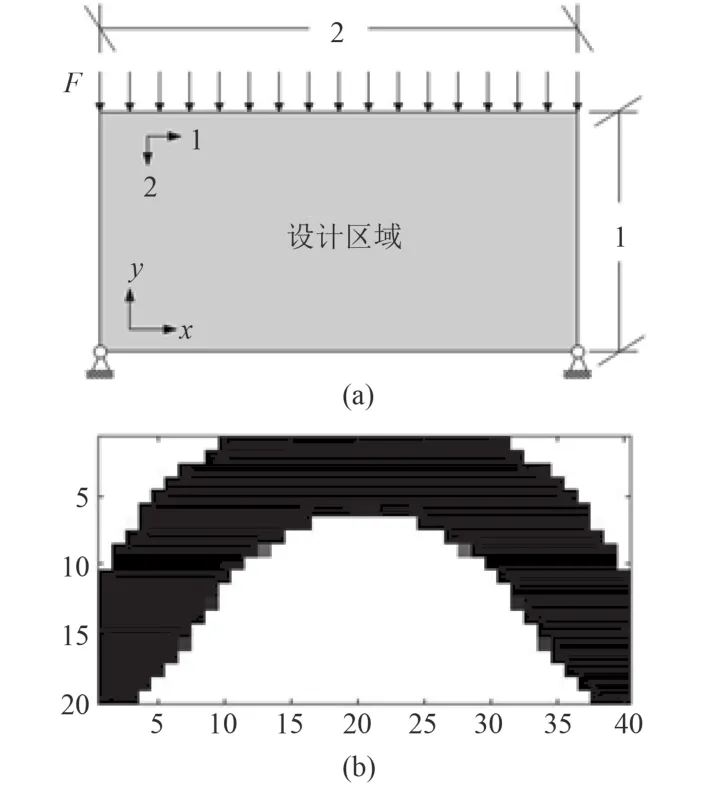
圖3 各向同性情況下，外部受壓的橋形結構計算模型及優化結果Fig. 3 Bridge-like structure with isotropic material subjected to pressure loading

在此算例中，平均靈敏度過濾方法[16]被用來消除計算中的數值不穩定現象。優化結果如圖 3（b），整體結構的最小柔順度為 271.358 6 J。對比文獻[13]中的結果，本文的計算結果與其非常相似。

為進一步研究復合材料對于拓撲優化結果的影響，假設材料的彈性模量分別為 E1= 2 100 GPa，，泊松比 v12= 0.3，復合材料的鋪層形式見表 1。其他條件均與圖 3（a） 相同。

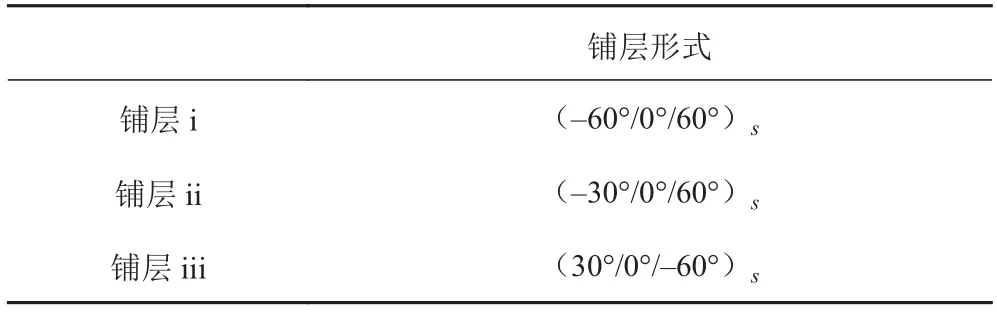
表1 復合材料鋪層形式Tab. 1 Three cases of different layups for the laminate composites

表1 中所列的 3 種鋪層形式的優化結果如圖 4 所示。圖 4（a） 為鋪層 i 的計算結果，結構的最小柔順度為 66.854 5 J，圖像與圖 3（b） 中的各向同性材料的優化結果相似，并且同樣為左右對稱結構；圖 4（b）為鋪層 ii 的計算結果，結構的最小柔順度為 84.607 2 J，優化后的圖像雖然仍然是橋形結構，但橋形結構不再是左右對稱，左半橋相較于右半橋更寬，橋形的頂部稍向右側偏移；圖 4（c） 為鋪層 iii 的計算結果，結構的最小柔順度為 84.607 2 J，優化后的結構最小柔順度與鋪層 ii 的結果完全相同，并且圖像與圖 4（b） 互為鏡像。

從上述結果中可發現，基于復合材料的拓撲優化結果與基于各向同性材料的結果存在著差異，優化結果中實體單元（即黑色單元）的分布與復合材料鋪層的角度有關。當某種復合材料鋪層的角度相互關于 90°對稱（如表 1 鋪層 i）時，優化結果呈左右對稱；當 2種鋪層形式的角度分別關于 0° 對稱（如表 1 鋪層 ii 與鋪層 iii）時，2 個優化結果鏡像對稱。

5.2 靜水壓下耐壓結構的優化設計

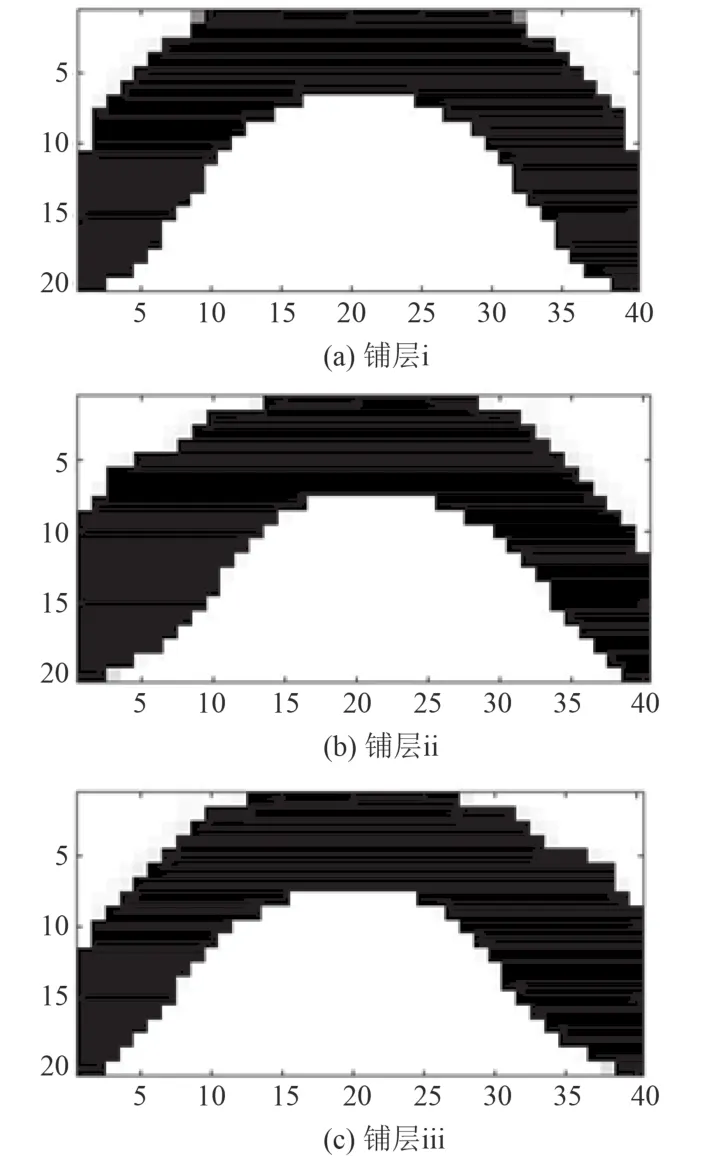
圖4 三種鋪層形式下的橋形結構優化結果Fig. 4 Optimal results of bridge-like structure with laminate composites

水下耐壓結構作為潛水器中的重要結構，其優化設計一直是一項引人關注的課題。在本算例中，僅考慮從結構的剛度方面進行優化設計，忽略諸多其他因素。則簡化后的耐壓結構的優化設計模型及其尺寸、邊界條件等如圖 5（a） 所示，正方形的設計區域四周受到靜水壓力，靜水壓大小為 2 MPa，并且在正方形 2條對稱軸上添加四處約束，使得對稱軸上的點僅能沿中心線方向移動。各向同性材料及復合材料的材料參數均與 5.1 節中的設定相同，實體材料占總設計區域的體積分數設為 10%。考慮到圖 5（a） 中的優化模型及邊界條件的對稱性，如圖 5（b） 取 1/4 模型作為優化對象，并離散成 40 × 40 個正方形單元。本例中，采用平面應變假設，并且分2步進行靈敏度過濾：第 1步，選擇平均靈敏度過濾方法[16]；第 2 步，選擇考慮密度梯度的靈敏度過濾方法[17]，其中取 α = 0.1。表 2所列為計算的所有材料及鋪層情況。

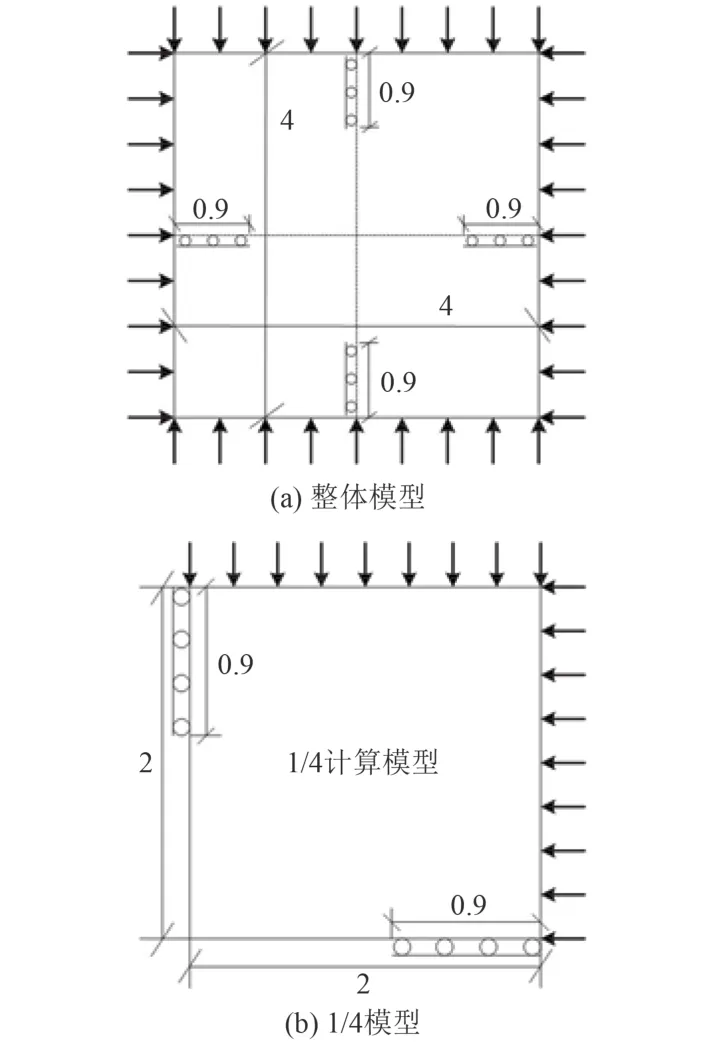
圖5 靜水壓下耐壓結構的計算模型Fig. 5 Computing model for underwater structure subjected to hydrostatic pressure

表2 考慮的各向同性材料及復合材料鋪層的情況Tab. 2 Cases of isotropic material and laminate composites considered

圖6 所示為各向同性材料及其他幾種復合材料鋪層形式下的耐壓結構優化結構。圖 6（a） 為各向同性材料的優化結果，其最終的柔順度為 229.283 8 J，最優拓撲形式接近 1/4 圓環，此結果與 Zheng 等[22]的優化結果的形狀非常相似；圖 6（b） ～ 圖 7（e）分別為對應表 2 中 Case 2～Case 5 的不同鋪層方式的拓撲優化結果，優化后的最終柔順度分別為 119.757 2 J，89.078 6 J，56.572 8 J，78.051 2 J，而從形狀上看，這些結果都接近 1/4 圓環，但是鋪層角度的不同會導致圓環寬度產生差異。Case 2～Case 5 的復合材料的鋪層方式的相似之處為都擁有 0° 鋪層，而不同之處為另一個鋪層（以下稱為“第2鋪層”）的角度不同。從圖 6（b） 和圖 6（c） 中可以看到，1/4 圓環靠近 0° 軸的一側的寬度明顯大于靠近 90° 軸的一側，而相應的 2 種鋪層方式中，第 2 鋪層的角度分別為 10° 和 30°，都比較接近 0°；圖 6（d） 顯示的結果中，圓環各處的寬度相對均勻，與圖 6（a） 的優化結果比較接近，這說明對于圖 5（b） 的優化問題，（0°/60°）s這種鋪層方式的效果與各向同性材料相似；從圖 6（e） 可以發現，此時的 1/4 圓環關于 45° 的對角線對稱，并且圓環中段的寬度大于兩端，在這種情況下，完整模型的最優拓撲形式應為圓柱，在沿著鋪層主向的方向上（即 0° 與 90°方向），圓柱的厚度最小，而沿著斜對角線方向（即45° 與 135° 方向），圓柱的厚度最大。

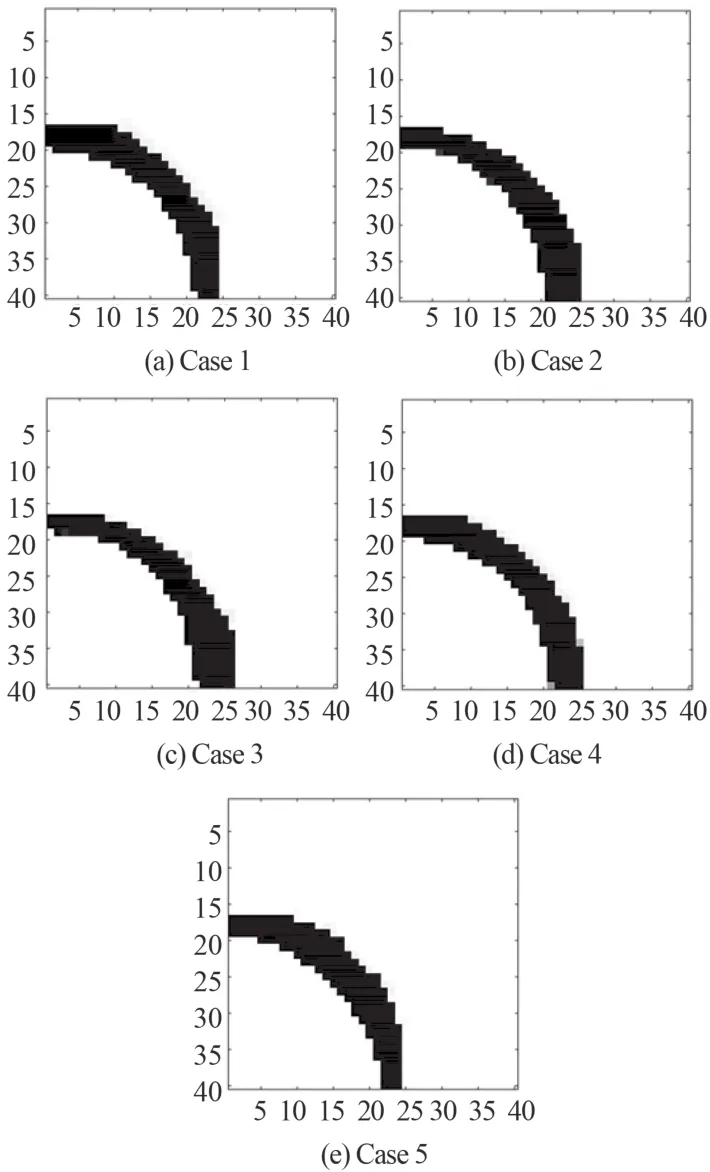
圖6 靜水壓下的耐壓結構優化結果Fig. 6 Optimal results of underwater structure subjected to hydrostatic pressure

5.3 內部鉸支的空心耐壓結構優化設計

在實際應用中，耐壓結構往往需要預留一定的內部空間用于容納物品或者人，因此，對于空心耐壓結構的優化設計對于耐壓殼體的設計具有一定的現實參考意義。與 5.2 節中設計區域為完整的正方形區域不同，本例中在長方形設計區域中間預留出一個小的長方形空白區域，同時考慮內部受約束的情況。設計模型及尺寸、邊界條件如圖 7（a） 所示，設計區域為灰色部分，設計模型的四周受到靜水壓力，靜水壓力大小為 2 MPa，并且在模型內部 8 處鉸支（即限制相應點出的垂直位移與水平位移）。計算模型的材料參數與 5.1 節的設定相同，實體材料占整個長方形區域的35%。如圖 7（b），取 1/4 模型作為優化對象，相應的尺寸及邊界條件如圖所示，將其離散成 100 × 40 個正方形單元。靈敏度過濾分2步進行：第 1 步，選擇平均靈敏度過濾方法[16]；第 2 步，選擇考慮密度梯度的靈敏度過濾方法[17]，其中取 α = 0.1。本例所計算的所有材料及鋪層情況同表 2。

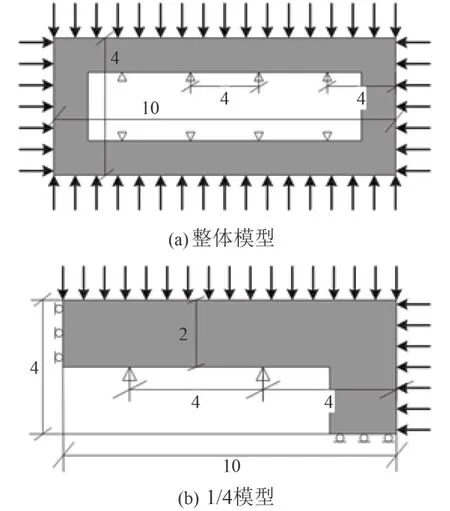
圖7 內部鉸支的空心耐壓結構的計算模型Fig. 7 Computing model for underwater structure with initial void and inside simply-supported constraints

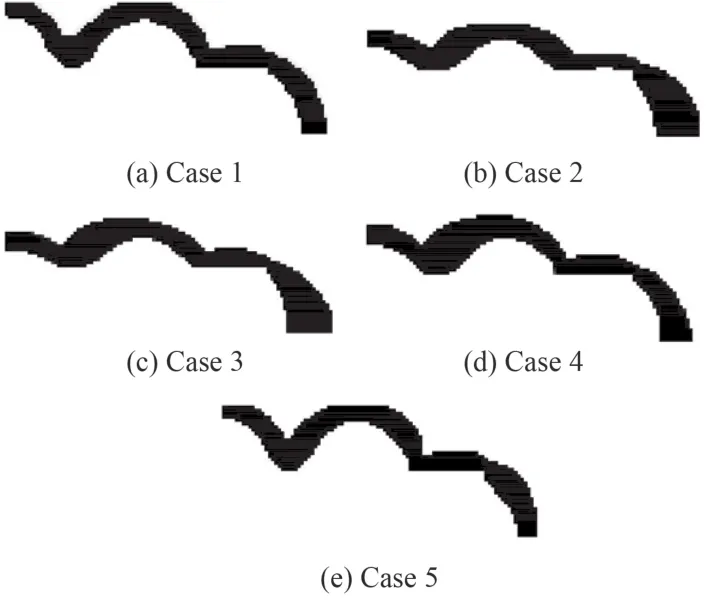
圖8 不同情形下內部鉸支的耐壓結構的優化結果Fig. 8 Optimal results of underwater structure with initial void and inside simply-supported constraints

圖8 所示為對應于表 2 所示的不同情形下的優化結果。圖 8（a） 為基于各向同性材料的優化結果，其最終的柔順度為 2 887.186 5 J，由此 1/4 模型的優化結果可以推測出完整模型的最優拓撲形式應為一個多球交接的連續殼體結構，此結果與 Wang[20]的計算結果非常相似；圖 8（b） ～ 圖 8（e） 分別對應于表 2 中 Case 2～Case5 的優化結果，最終的柔順度分別為 1 492.517 3 J，1 092.020 4 J，869.415 1 J，999.741 1 J，這些拓撲形式大體上都有著類似于各向同性情況的結構，但在局部結構的細節上又存在著差異。比較這些結果可以發現，第 2 鋪層角度越接近 0°，優化結果中拱形的高度越低，而拱的兩邊的寬度差越小；隨著第 2 鋪層角度的增大，結構的最小柔順度值先逐漸變小，達到某一角度后柔順度值出現回升；而在優化結果中，拱形兩邊的寬度差隨角度的增大而增大；同時，如果第 2 鋪層的角度為 90°（即 Case 5），其最優拓撲形式基本與各向同性的情況相同，拱形兩邊的寬度差異也不大。另外，從圖 7（a） 中可以推斷，這種內部鉸支的空心耐壓結構的最優拓撲形式可能會在殼體連接處出現應力集中的情況，進而可能導致結構的失效。而根據圖 8（b）～ 圖8（d） 的結果，可以提出猜想：選擇合適鋪層的復合材料作為此種耐壓結構的主材料，對應的最優拓撲形式的殼體連接處更平緩，可能會減少應力集中出現的情況。

圖9 是王存福[23]于 2014 年提出的通過拓撲優化發現的多球鉸接模型，通過本節的優化模型可以發現，圖 8 中各向同性材料的結果的拓撲形式與圖 9 一致，說明了本文方法的有效性，但隨著鋪層的變化，其優化結構也發生了一定的變化，說明復合材料的應用對于未來深潛器耐壓結構新形式的探索具有重要的工程意義。圖 10 為 MIT 水下潛器設計團隊[24]給出的一種多球交接耐壓殼體模型圖，該概念的提出說明在未來多球交接模型講有著廣闊的應用前景，本文優化結構拓展至三維將給出不同鋪層狀態下的多球交接耐壓結構形式，對于發展該種耐壓結構的設計具有指導意義。

圖9 材料各向同性多球鉸支的耐壓結構Fig. 9 Optimal results of multiple intersecting spherical pressure hull with isotropic material

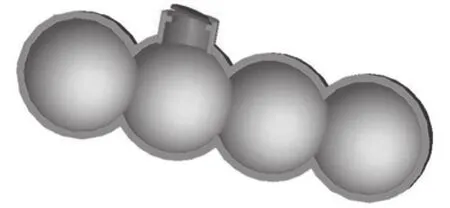
圖10 MIT 提出的多球交接耐壓結構模型Fig. 10 Conceptual model of multiple intersecting spherical pressure hull

6 結 語

本文通過推導復合材料的等效剛度矩陣，并結合SIMP 模型，等值線方法以及平均敏度方法與考慮密度梯度的靈敏度過濾方法，實現了對在拓撲相關載荷作用下，基于復合材料的拓撲優化問題的研究。在本文中，計算分析了 3 個算例：外部受壓的經典橋形結構優化算例，靜水壓作用下的耐壓結構優化設計算例，以及內部鉸支的空心耐壓結構優化設計算例。可以得出以下幾個結論：

1）對于同一個優化設計問題，采用復合材料得到的優化結果與采用各向同性材料得到的結果在結構大體上相似，但局部結構會存在差異；

2）復合材料的鋪層方式不同，優化結果也可能不同：如果是非對稱鋪層，優化結果很可能出現不對稱的結構；如果 2 種鋪層方式完全相反，兩者的優化結果可能會是互成鏡像；

3）對于有2個鋪層的復合材料，鋪層角度的變化，會改變實體材料的分布，對最優拓撲形式產生較大影響；

4）對于靜水壓作用下的耐壓結構及空心耐壓結構，復合材料的應用有可能消除或削弱原優化結果中的應力集中等不良現象。本文的研究只是對基于復合材料的拓撲優化在水下耐壓結構設計上的初步應用，諸如基于復合材料的三維拓撲優化問題，以及更多形式的耐壓結構設計問題等都是值得進一步探究的課題。

[1]BOWEN A D, YOERGER D R, TAYLOR C, et al. The Nereus hybrid underwater robotic vehicle for global ocean science operations to 11, 000m depth [C]// Oceans. 2008:1–10.

[2]MICHELL A G M. The limit of economy of material in frame structures [J]. Philosophical Magazine Ser, 1904, 8. 589–597.

[3]BENDSOE M P, KIKUCHI N. Generating optimal topologies in structural design using a homogenization method [J].Computer Methods in Applied Mechanics & Engineering,1988, 71(2): 197–224.

[4]SUZUKI K, KIKUCHI N. A homogenization method for shape and topology optimization [J]. Computer Methods in Applied Mechanics and Engineering, 1991, 93(3): 291–318.

[5]BENDSOE M P. Optimal shape design as a material distribution problem [J]. Structural Optimization, 1989, 1(4):193–202.

[6]ZHOU M, ROZVANY G I N. The COC algorithm, Part II:Topological, geometrical and generalized shape optimization[J]. Computer Methods in Applied Mechanics & Engineering,1991, 89(1-3): 309–336.

[7]SIGMUND O. On the design of compliant mechanisms using topology optimization [J]. Mechanics of Structures &Machines, 1997, 25(4): 493–524.

[8]MLEJNEK H P, SCHIRRMACHER R. An engineer’s approach to optimal material distribution and shape finding [J].Computer Methods in Applied Mechanics & Engineering,1993, 106(1-2): 1–26.

[9]SIGMUND O. Design of material structures using topology optimization [D]. Denmark: Technical University, 1994.

[10]BENDSOE M P, SIGMUND O. Material interpolation schemes in topology optimization [J]. Archive of Applied Mechanics, 1999, 69(9): 635–654.

[11]MAUTE K, RAMM E. Adaptive topology optimization [J].Structural Optimization, 1995, 10(2): 100–112.

[12]HAMMER V B, OLHOFF N. Topology optimization of continuum structures subjected to pressure loading [J]. Structural and Multidisciplinary Optimization, 2000, 19(2): 85–92.

[13]DU J, OLHOFF N. Topological optimization of continuum structures with design-dependent surface loading-Part I: new computational approach for 2D problems [J]. Structural and Multidisciplinary Optimization, 2004, 27(3): 151–165.

[14]LEE D, SHIN S, TUAN L A, et al. Computational MATLAB-based optimal design of laminated composite plates [C]// Proc.5th European Conference of Computer Science, Recent Advances in Information Technology. Geneva, Switzerland,2014.

[15]BORRVALL T. Topology optimization of elastic continua using restriction [J]. Archives of Computational Methods in Engineering, 2001, 8(4): 351–385.

[16]SIGMUND O. Morphology-based black and white filters for topology optimization [J]. Structural and Multidisciplinary Optimization, 2007, 33(4): 401–424.

[17]龍凱, 傅曉錦. 考慮密度梯度的敏度過濾方法[J]. 計算機輔助設計與圖形學學報, 2014, 26(4): 669–674.

LONG Kai, FU Xiao-jin. Sensitivity filtering method considering density gradient [J]. Journal of Computer-Aided Design & Computer Graphics, 2014, 26(4): 669–674.

[18]張維聲, 孫國, 郭旭, 等. 基于水平集描述的結構拓撲與構件布局聯合優化新方法[J]. 工程力學, 2013, 30(7): 22–27.

ZHANG Wei-sheng, SUN Guo, GUO Xu, et al. A level setbased approach for simultaneous optimization of the structural topology optimization and the layout of embedding structural components [J]. Engineering Mechanics, 2013, 30(7): 22–27.

[19]SVANBERG K. The method of moving asymptotes—a new method for structural optimization [J]. International Journal for Numerical Methods in Engineering, 1987, 24(2): 359–373.

[20]WANG Cun-fu, ZHAO Min, GE Tong. Structural topology optimization with design-dependent pressure loads [J].Structural and Multidisciplinary Optimization, 2015: 1–14.

[21]MICHALERIS P, TORTORELLI D A, VIDAL C A. Tangent operators and design sensitivity formulations for transient nonlinear coupled problems with applications in elastoplasticity[J]. International Journal for Numerical Methods in Engineering, 1994, 37(14): 2471–2500.

[22]ZHENG B, CHANG C J, GEA H C. Topology optimization with design-dependent pressure loading [J]. Structural and Multidisciplinary Optimization, 2009, 38(6): 535–543.

[23]王存福. 水下耐壓殼體拓撲優化設計方法探究[D]. 上海：上海交通大學, 2013.

[24]http://web.mit.edu/12.000/www/m2005/a2/finalwebsite/equip ment/manned/hull.shtml.

Topology optimization design of underwater pressure structure with laminate composites

DAI Yang1, FENG Miao-lin1, ZHAO Min1,2
(1. State Key Laboratory of Ocean Engineering, Shanghai Jiaotong University, Shanghai 200240, China;2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China)

The paper studies the application of topology optimization with laminate composites in the design of underwater pressure structure. The methodology is based on the isoline method, the solid isotropic material with penalization(SIMP) model, and sensitivity filtering techniques. In addition, the equivalent element stiffness matrix for laminate composites is derived. By computing topology design cases of classical bridge-like structure, underwater structure subjected to hydrostatic pressure, and underwater pressure structure with initial void, the influence on the optimal result of structure under design-dependent loads taken by composites is analyzed. It is found that the structural optimization results of composite material and isotropic material are similar. The change of the angle and laminated type of composite layups may have a large influence on the optimal form of structure. There are similarities between the optimization results of pressure structure with initial void obtained in this paper and the concept put forward by MIT team. Therefore, the research of topology optimization with composite material will make contributions to the design of underwater pressure structure in the future.

pressure structure；topology optimization；composite material；design-dependent loads

U663.1；U674.941

A

1672 – 7649(2017)10 – 0014 – 08

10.3404/j.issn.1672 – 7649.2017.10.003

0 引 言

潛水器是探索深海的重要工具，目前研究人員對于開發新型高性能深潛器的需求日益突出。而作為深潛器結構中核心部分的水下耐壓結構，對其優化設計，探尋新的耐壓結構的最優拓撲形式有著重大的應用價值。在傳統的耐壓結構的設計中，形成了在淺水中采用圓柱形耐壓殼，在深水中采用球形耐壓殼的固定觀念。如我國 7 000 m 載人深潛器“蛟龍”號的耐壓結構部分就選用了鈦合金球形耐壓殼。但隨著科學技術的發展與復合材料的應用，這些傳統的觀念被打破。在 2009 年，由美國伍茲霍爾海洋研究所研制的“海神”號無人潛水器成功到達了馬里亞納海溝的10 902 m 深處[1]。而為了實現“海神”號的最輕化，同時保證足夠的結構強度，其耐壓結構選用了質量輕、強度高的陶瓷材料，并且其形狀不再是傳統的球形，而是圓柱形的耐壓殼。目前，國外開展了基于復合材料的耐壓結構優化設計研究，由于復合材料的輕質，未來基于復合材料的耐壓結構將成為潛器設計的重要發展方向。

2016 – 10 – 21；

2016 – 10 – 26

戴揚(1991 – )，男，碩士研究生，研究方向為復合材料結構拓撲優化。