基于AGPF的滾動軸承性能衰退趨勢預測
,
(西北工業大學 動力與能源學院,西安 710129)
基于AGPF的滾動軸承性能衰退趨勢預測
史曉雪,吳亞鋒
(西北工業大學動力與能源學院,西安710129)
針對粒子濾波算法中粒子退化和計算復雜度問題,提出了一種自適應遺傳粒子濾波(AGPF)算法;該算法采用遺傳算法代替傳統粒子濾波中的重采樣方法,并根據粒子數與濾波誤差方差之間的關系,自適應調節濾波過程中的粒子數;通過預測滾動軸承的性能衰退趨勢,對該方法進行驗證,結果表明,AGPF算法能夠在保證預測精度的條件下,減少濾波粒子數,更加適用于滾動軸承的性能衰退趨勢預測。
滾動軸承;自回歸模型;粒子濾波;衰退趨勢預測
0 引言
滾動軸承是決定機械設備健康狀態的關鍵部件之一,及時、準確地預測軸承性能衰退趨勢,可有效延長設備運行時間,降低維護成本。
近年來,有關滾動軸承故障診斷與壽命預測的新方法不斷涌現,粒子濾波就是其中之一。粒子濾波算法(Particle Filtering,PF)源于蒙特卡洛的思想,通過非參數化的蒙特卡洛模擬方法來實現遞推貝葉斯濾波。該方法適用于任何能用狀態空間模型描述的非線性系統,精度可以逼近最優估計。粒子濾波可被應用于滾動軸承振動信號降噪處理[1],但其存在的粒子退化問題會影響降噪的效果。對此,可將遺傳算法(Genetic Algorithm)和粒子濾波相結合,引導粒子向高似然區域移動,防止粒子退化現象。遺傳粒子濾波(GPF)算法將遺傳算法中的的選擇、交叉和變異操作引入到粒子濾波中,代替傳統的重采樣方法。GPF算法增加了有效粒子數,改善了濾波精度,但也增加了濾波復雜度。
提出了一種自適應遺傳粒子濾波算法(AGPF),并將其應用于滾動軸承的性能衰退趨勢預測。首先介紹了傳統粒子濾波算法和遺傳粒子濾波算法,其次在此基礎上給出了自適應遺傳粒子濾波算法,最后利用AGPF方法對滾動軸承性能衰退趨勢進行預測。
1 傳統粒子濾波算法
任一動態系統的狀態空間模型可以表示為:
xk=f(xk-1,vk)
(1)
yk=h(xk,nk)
(2)
上面兩式中,式(1)所描述的是狀態轉移方程,式(2)所描述的是觀測方程。xk為系統狀態在k時刻對應的狀態變量,yk為觀測值,表示的是xk對應的觀測值,vk為系統噪聲,nk為觀測噪聲,vk和nk相互獨立。
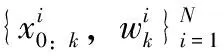
(3)
(4)
假設重要密度可以分解為:
q(x0:k|z1:k)=q(xk|x0:k-1,z1:k)q(x0:k-1|z1:k-1)
(5)
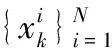
由于后驗概率密度函數可表示為:
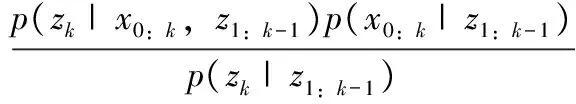
∝p(zk|xk)p(xk|xk-1)p(x0:k-1|z1:k-1)
(6)
將式(6)和式(5)代入(4),可得重要性權值更新公式為:
(7)
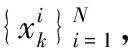
(8)
標準粒子濾波算法選擇易于實現的先驗概率密度作為重要密度函數,即:
(9)
將式(9)代入式(8),重要性權值可簡化為:
(10)
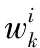
(11)
而后驗概率密度p(xk|z1:k)可表示為:
(12)
2 自適應遺傳粒子濾波算法
傳統粒子濾波存在的主要問題是粒子退化,即隨著濾波迭代次數的增加,大部分粒子的權重會變得很小,而只有少部分粒子的權重比較大,這就意味著大量的計算將浪費在那些權重極小的粒子上。遺傳算法是模擬達爾文生物進化論的自然選擇和遺傳學機理的生物進化過程的計算模型,是一種通過模擬自然進化過程搜索最優解的方法。它反映的是一種進化思想,利用這個思想,可以將遺傳算法中的選擇、交叉、變異等進化運算引入到粒子濾波算法的重采樣步驟中,構成遺傳粒子濾波算法。
遺傳粒子濾波算法中的選擇、交叉、變異操作實現步驟描述如下:
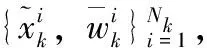
(13)
(14)
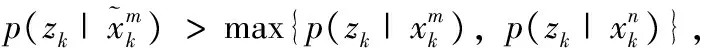
(15)
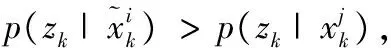
遺傳粒子濾波算法可以有效增加粒子多樣性,解決粒子退化問題,但由此也帶來了計算過程復雜、計算量大的問題。通常,PF和GPF算法中的粒子數為定值,選取的粒子數越多,濾波精度越高,但過多的粒子數會對計算帶來沉重的負擔。為了降低計算復雜度,且保持原有的濾波精度,可使得濾波過程中的粒子數隨著濾波精度的變化而變化,當濾波精度較高時,少量的粒子數就可以滿足精度要求,當濾波精度較低時,需要大量的粒子數來提高精度。由此提出自適應選取粒子數的方法,其基本思想是:由粒子數與濾波誤差方差之間的關系自適應地調節粒子數。粒子數選取函數[2]可表示為:
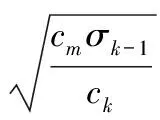
(16)
其中:cm為精度代價因子,ck為實時代價因子,σk-1為濾波誤差方差。
綜上,自適應遺傳粒子濾波算法具體步驟可歸納如下:
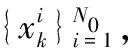
2)權值更新。在k時刻,更新粒子權值:
(17)
并且歸一化:
(18)
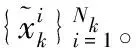
4)狀態估計。
(19)
方差估計:
(20)
5)粒子數選取:
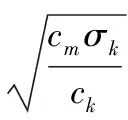
(21)
7)時刻k=k+1,轉到第2步。
3 滾動軸承性能衰退趨勢預測
利用美國凱斯西儲大學電氣工程實驗室滾動軸承實驗平臺采集到的振動數據,對滾動軸承性能衰退趨勢進行預測,以驗證AGPF算法的準確性。
3.1 滾動軸承性能衰退趨勢預測流程
滾動軸承的性能衰退趨勢預測,主要分為軸承性能變化趨勢描述、模型建立和性能預測3個方面。流程如圖1所示。
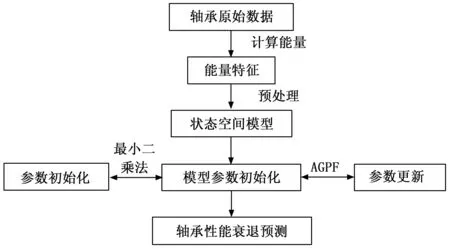
圖1 AGPF的軸承性能衰退預測流程圖
流程描述如下:
1)計算不同狀態下滾動軸承振動數據的能量特征,描述其能量特征變化趨勢;
2)以滾動軸承能量特征變化趨勢為基礎,建立自回歸模型,確定模型階次及參數,得到初始;
3)將該模型作為AGPF的狀態空間模型,模型參數采用最小二乘法初始化,得到參數初始值,再通過AGPF算法對模型參數進行更新,優化模型參數,提高模型準確性;
4)利用最終獲得的模型進行遞推預測,實現滾動軸承的性能衰退趨勢預測。
3.2 滾動軸承性能變化趨勢
凱斯西儲大學的滾動軸承用電火花加工單點損傷,在其內圈、外圈和滾動體處設置了直徑分別為0.007英寸、0.014英寸、0.021英寸、0.028英寸的損傷。在電動機的驅動端放置加速度傳感器來采集故障軸承的振動加速信號。振動信號由16通道數據記錄儀采集得到,采樣頻率為12 kHz,采樣時間10 s。
選取1 797 rpm轉速下滾動軸承內圈單點損傷直徑為0(正常狀態)、0.007英寸、0.014英寸、0.021英寸、0.028英寸5種狀態的振動數據為基礎,通過計算其能量特征得到滾動軸承的性能變化過程。表1給出了上述5種損傷狀態下的振動能量值。

表1 不同損傷尺寸對應的能量
由表1可知,5種不同損傷狀態下的能量特征隨著損傷尺寸的增加呈非線性增長,但僅由上述數據無法得到滾動軸承能量連續變化過程,因此,對表1給出的數據進行三次樣條插值處理,得到滾動軸承能量連續變化情況如圖2所示。
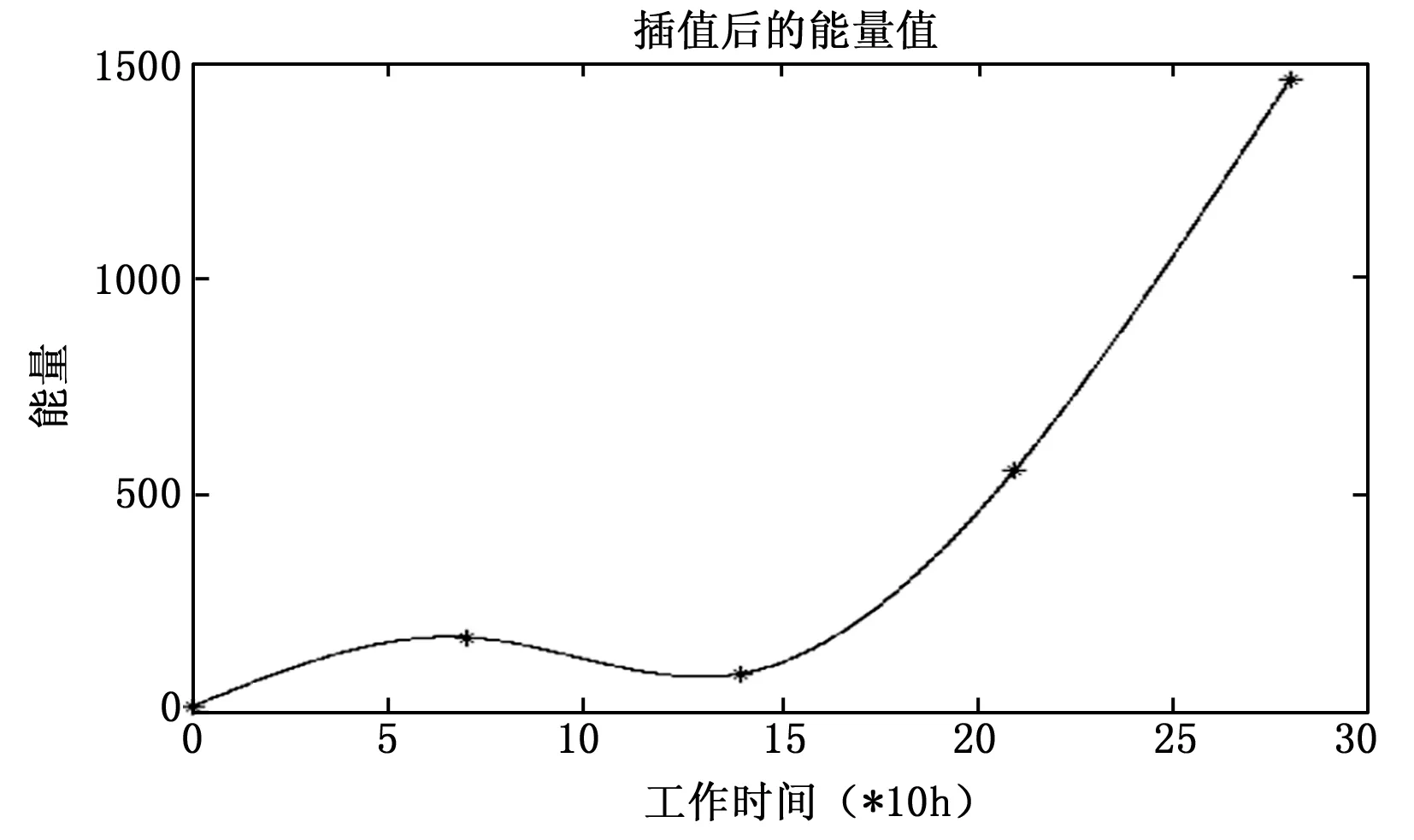
圖2 能量信號插值
假設損傷直徑變化0.001英寸所耗費的時間是10小時,圖2顯示了280個小時內滾動軸承的能量變化情況。
3.3 滾動軸承性能衰退趨勢預測
從圖2中的能量信號變化過程可以看出,滾動軸承的能量變化信號具有非平穩性,因此,需要對該信號做差分運算,將其轉化為平穩信號進行后進行AR建模。以0.001英寸為間隔,選擇前21組能量數據,以AIC準則確定模型最佳階數為2階,采用最小二乘法計算得到2階AR模型為:
xk=1.5833xk-1-0.6484xk-2
(22)
將式(22)給出的初始模型作為AGPF的狀態方程,模型參數作為初始值,選擇初始粒子數為N=500,通過AGPF算法對其參數進行更新,優化模型參數,得到更加精確的模型。進一步通過該模型對21組之后的能量特征進行預測,之后對所有數據做反差分運算,得到真實的預測結果。
為了驗證AGPF預測算法的準確性,分別采用PF、GPF預測方法和其進行比較,結果如圖3和圖4所示。
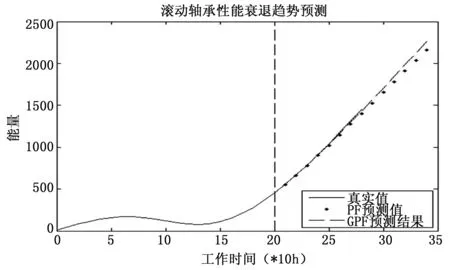
圖3 PF與GPF預測結果
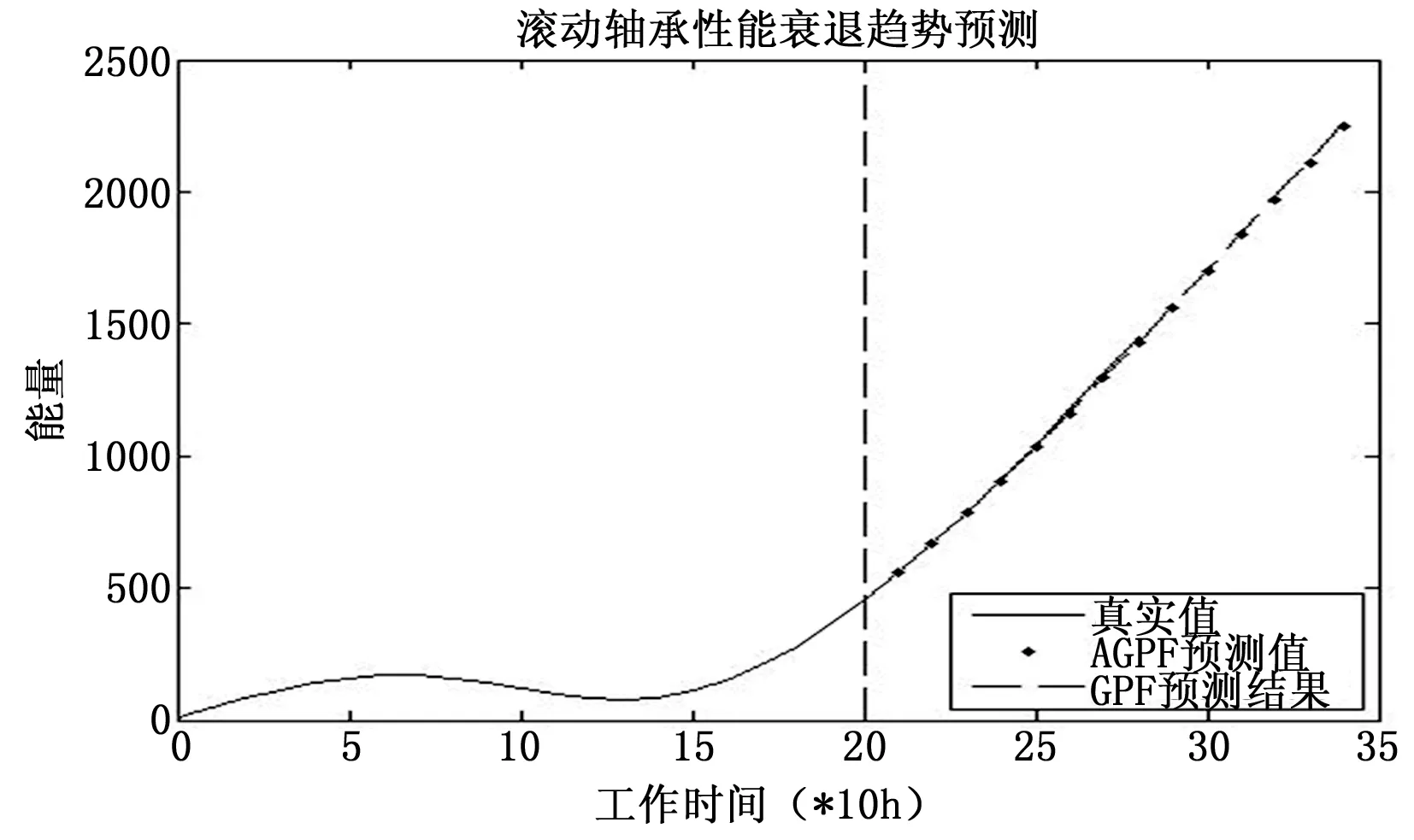
圖4 GPF與AGPF預測結果
從圖中3和圖4顯示的預測結果中可以看出,GPF的預測結果比PF的預測結果更接近真實值,AGPF的預測結果與GPF的預測結果基本一致。
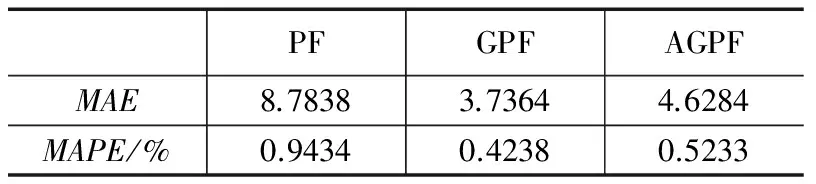
為了進一步說明AGPF方法預測的有效性,計算從22到29組預測數據的平均絕對誤差(MAE)和平均百分比誤差(MAPE),結果如表2所示。
表2 軸承壽命預測結果對比
PFGPFAGPFMAE8.78383.73644.6284MAPE/%0.94340.42380.5233
從表2的MAE和MAPE定量分析來看,相比于其它兩種改進算法,PF 算法的MAE和MAPE值最高,預測精度較低。AGPF與GPF算法的MAE和MAPE值相差不多,約為PF算法的1/2,預測精度較高。GPF的濾波精度比PF高,但計算過程變得復雜,為此,AGPF利用粒子數與濾波誤差方差之間的關系,自適應地調節粒子數,并達到與GPF相當的濾波精度。圖5描述了濾波過程中自適應調節粒子數時粒子的變化情況。
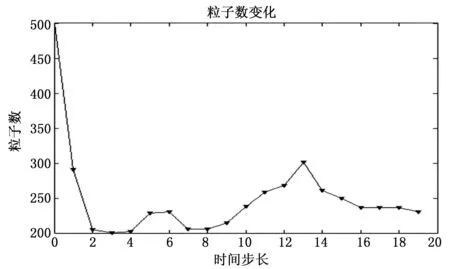
圖5 粒子數變化情況
在圖5中,初始粒子數為500,在后續的濾波過程中,粒子數的波動范圍為200~300,粒子數的減少,使得濾波過程中的復雜度降低,復雜度變小。
4 結論
提出了一種自適應遺傳粒子濾波算法,并將其應用于滾動軸承的性能衰退趨勢預測。AGPF算法采用遺傳算法代替傳統粒子濾波中的重采樣方法,并根據粒子數與濾波誤差方差之間的關系,自適應調節濾波過程中的粒子數,解決了粒子退化及計算過程復雜度問題。將AGPF算法應用于滾動軸承性能衰退趨勢預測,分別對PF、GPF和AGPF算法的濾波效果進行了驗證,結果表明,AGPF算法在確保預測精度的前提下降低
了計算的復雜度,更適合于軸承的性能衰退趨勢預測。
[1] 潘宏俠, 門吉芳. 粒子濾波在軸承故障振動信號降噪中的應用[J]. 振動、測試與診斷, 2011, 31(3): 354-356.
[2] 胡建旺, 張 淼. 自適應采樣數粒子濾波算法[J]. 軍械工程學院學報, 2009, 21(3): 55-58.
[3] 闕子俊. 基于UKF的軸承剩余壽命預測方法研究[J]. 儀器儀表學報, 2016, 37(9): 2036-2043.
[4] Li N P, Lei Y G. An Improved exponential model for predicting remaining useful life of rolling element bearings[J]. IEEE Transactions on Industrial Electronics, 2015, 62(12): 7762-7773.
[5] Qian Y N, Yan R Q. Remaining useful life prediction of rolling bearings using an enhanced particle filter[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(10): 2696-2707.
[6] 吳 昊, 孫曉燕, 郭玉堂. 保持粒子多樣性的非退化粒子濾波方法研究[J]. 電子學報, 2016, 44(7): 1734-1741.
[7] Li N P, Lei Y G, Liu Z Y,et al. A particle filtering-based approach for remaining useful life predication of rolling element bearings[A]. 2014 IEEE Conference on Prognostics and Health Management (PHM)[C]. IEEE, 2014.
PredictionofDecliningPerformanceofRollingBearingBasedonAGPF
Shi Xiaoxue,Wu Yafeng
(College of Power and Energy, Northwestern Polytechnical University, Xi′an 710129, China)
Aiming at the problem of particle degradation and computational complexity in particle filter algorithm, an adaptive genetic particle filter (AGPF) algorithm is proposed. The algorithm uses the genetic algorithm instead of the resampling method in the traditional particle filter, and adaptively adjusts the number of particles in the filtering process according to the relationship between the number of particles and the variance of the filter error. The results show that the AGPF algorithm can reduce the number of filtered particles under the condition of ensuring the prediction accuracy, and is more suitable for the prediction of the performance of the rolling bearings.
rolling bearings; autoregressive model; particle filter; forecast of recession trend
2017-07-14;
2017-08-14。
史曉雪(1992-),女,甘肅白銀人,碩士研究生,主要從事信號與信息處理方向的研究。
吳亞鋒(1961-),男,陜西西安人,教授,博士生導師,主要從事現代信號處理理論與方法、計算機測控技術、振動噪聲分析與控制方向的研究。
1671-4598(2017)10-0228-04
10.16526/j.cnki.11-4762/tp.2017.10.058
TP391
A

