基于加權幾何精度因子(WGDOP)的地基導航系統評價方法

, , ,長水

(1.國防科學技術大學 機電工程與自動化學院，長沙 410073; 2.陸航駐北京地區軍事代表室，北京 100101)

基于加權幾何精度因子(WGDOP)的地基導航系統評價方法

楊楠1,李昊2,劉凱1,劉長水1

(1.國防科學技術大學機電工程與自動化學院，長沙410073; 2.陸航駐北京地區軍事代表室，北京100101)

為了評價衛星導航系統中位置估計的性能，GDOP作為一種衡量測量誤差和定位誤差之間幾何關系的評價方法被廣泛應用;由于地基導航系統各個單元的測量誤差不同，且受用戶距離影響不可忽略，需要對與距離有關的評價標準進行研究；因此，提出使用WGDOP代替GDOP作為評判標準，從分析地基導航系統誤差方差入手，對WGDOP表達式進行詳細分析，通過系統比較兩種定位因子，說明采用WGDOP作為地基導航系統基站布設評價標準,準確性高;研究結果表明，采用加權幾何精度因子作為評價標準，可以更適應地基導航系統的實際使用環境，對系統定位性能進行更精確的評價，對精度因子評估有明顯改善。

地基導航系統；加權幾何精度因子；幾何精度因子

0 引言

全球定位系統(GPS)是美國國防部為了滿足軍方和民用領域對實時、連續、精確導航的需求所提出的方案，它基于人造衛星，是面向全球的全天候無線定時、定位系統。衛星導航系統由于具有覆蓋范圍廣、全天候全天時、用戶數量無限制等優點，被作為世界范圍內首選的定位導航授時手段。但它的使用具有一定局限性，在一些特定使用場景下，如室內、山谷或高樓林立區，由于信號的物理特性、星座布局和環境等影響因素，導致衛星定位系統產生定位精度不佳、衛星遮擋嚴重、完好性和可靠性較差、信號功率較弱、抗干擾能力不足等問題[1-3]。

為了解決以上問題，大量學者提出使用偽衛星對衛星導航系統性能進行增強。隨著導航定位領域的科學技術的飛速發展，新型地基導航系統也被提出，該系統最早被澳大利亞的Locata公司提出，其最大的優勢在于：不依賴于原子鐘以及外部輔助，僅利用站間精確時間同步技術即可使網內的基準站達到亞ns級的時間同步，從而可以完全獨立于衛星導航系統工作，以達到增強衛星導航系統的目的[4]。

在定位導航系統中，系統定位精度代表系統解算位置結果與用戶實際位置結果之間的差異，而精度評估則是判斷解算值與真值一致的離散程度。測量誤差和幾何精度因子(GDOP)是影響衛星導航系統定位精度的兩大重要因素，其中，測量誤差與系統性能有關，而幾何精度因子GDOP的大小依賴于星座(基站)布局的好壞。在測量誤差一定的情況下，定位系統的定位精度主要取決于系統星座分布情況。針對全球衛星定位系統，由于其衛星幾乎處于同一軌道高度，一般假設所有偽距測量誤差相互獨立，具有相同零均值且均方根相等，進而使用幾何定位因子(GDOP)對系統進行定位精度評估。

地基導航系統與衛星導航系統類似,其定位精度也可表達成測量誤差和精度因子相乘的形式，但是地基導航系統與衛星導航系統布局方案的最大區別在于：地基導航系統基站完全布設于地面上，用戶到各基站的距離變化較大，導致對各基站的偽距測量誤差存在顯著差異，并不能夠視為相同。因此使用傳統定位因子GDOP對地基導航系統進行布局可能并不適用，因此還需對加權幾何精度因子(WGDOP)進行研究，從而得到使系統定位精度更準確的定位精度評估方法。

對于不同類型衛星組成的北斗導航系統以及不同導航系統組成的組合系統(如GPS/GLONASS組合系統)，進行定位時由于不同的誤差導致對衛星單元影響不同，從而測距精度也不相同，若使用假設觀測值具有相同測量誤差的幾何精度(GDOP)評價方法，則不能客觀表示定位精度。因此加權精度因子在一些文獻中被提出。

本文通過分析適用于地基導航系統的WGDOP表達式,并通過仿真實驗對GDOP及WGDOP兩種評價方法進行分析比較，從而選擇更加準確的方法對系統進行定位精度評估。

1 地基導航系統定位原理

地基導航系統若想實現定位，則必須先解決接收機的兩個問題，一是確定各基站在空間中的準確位置，二是得到從基站到接收機的精確距離。解決以上兩個基礎必備問題后，就可采用偽距定位原理，對用戶接收機位置進行精確定位。

與衛星導航系統相似，地基導航系統也采用偽距實現定位、定時的基本原理：接收機通過內部碼跟蹤環路上的C/A碼發生器和C/A碼相關器獲得測距碼相位(CP)，與解調出的各基站導航電文數據碼結合，得出接收機與該基站的偽距測量值ρ(n)。該測量值并不代表接收機與基站的幾何距離。

不同于衛星導航系統，地基導航系統基站導航信號不經過電離層，因此考慮基站、接收機分別與系統時間存在鐘差δts、δtu，以及折射效應導致電磁波在大氣中傳播存在的傳播時延，可得偽距觀測方程為：

ρ=r+c(δtu-δts)+T+ερ

(1)

其中:r為用戶接收機與基站的幾何距離；T為對流層延遲對應的距離量；ερ為偽距測量噪聲。

地基導航系統定位原理如圖1所示，定義誤差校正后的偽距測量值表達式如下：

(2)

其中：(x(n),y(n),z(n))為基站n空間位置坐標，(x,y,z)為用戶接收機位置坐標。

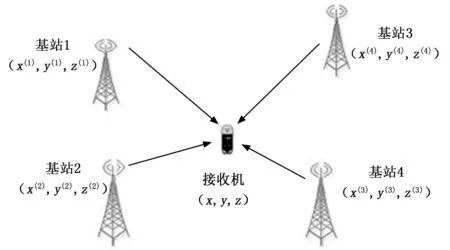
圖1 地基導航系統定位原理

從而，地基導航系統定位定時算法的本質就是求解由用戶三維位置坐標及鐘差4個未知數組成的一個四元非線性方程組：

(3)

2 地基導航系統布局評價準則

大量學者在研究過程中，為了準確評價偽衛星導航定位系統布局方案的優劣及定位性能的精度大小，提出了很多用來評價導航系統布局對定位精度影響的方法，比如幾何精度因子(GDOP)法——用來直觀顯示系統布局對定位精度的影響；克拉美-羅下界(CRLB)法——主要用來解決高斯平穩信號的估計問題；均方誤差及均方根誤差(MSE)法——用來表明參數真值與參數估計值之差的平方的期望值；圓/球誤差概率(CEP)法——用來表示以誤差均值為中心，隨機矢量為半徑的圓。其中，因為精度因子計算較為簡單且表現較為直觀，常被直接用來衡量系統基站布局對定位精度的影響。

2.1 幾何精度因子(GDOP)

根據參考文獻[5]中對定位誤差協方差進行的分析，可以發現系統定位誤差等于接收機測量誤差乘以一個放大倍數，導航學將該與系統星座(基站)幾何布局有關的定位誤差放大倍數定義為幾何精度因子(GDOP)，它代表系統測量誤差引起的基站(星座)到用戶接收機之間距離偏差的放大倍數。由于GDOP只與星座幾何分布有關，因此常被用來評價系統星座(基站)布局的優劣。

在制定系統布局方案中，GDOP通常被用于從所有星座(基站)中選出使系統定位精度最高的布局方案，或者通過對基本幾何圖形進行GDOP分析，從而得到地面基站的一般布局方法。該評價方案以所有基站(星座)的測量量具有相同的測量誤差為前提，通過遍歷所有可用基站的布局方案，得到擁有最小精度因子(GDOP)的幾何布局方案，從而利用該最優布局方案進行最精確的定位。

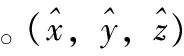
(4)

其中:

(5)

(6)

(7)

該評價標準表明，在定位誤差不變的條件下，GDOP值越小，定位精度越高，基站(星座)布局越合理。除了GDOP，根據實際場景的不同需求，還可選擇PDOP(空間位置精度因子)、HDOP(水平位置精度因子)、VDOP(高程精度因子)、TDOP(時間精度因子)。

不難發現，在GDOP推導過程中，需要將各衛星(基站)測量值的測量誤差視為相等。在實際中，接收機需要根據基站(星座)仰角高低和接收機跟蹤環路的運行狀態以及信號強弱等因素，對不同時刻的不同測量值進行估算，而不能視為全部相等。

由于在衛星導航系統中，衛星與用戶距離很遠，星座仰角及信號強弱等變化不大，故可使用該評價標準。然而，在地基導航系統應用環境中，由于基站布設于地面或者近地面，各基站到用戶的距離明顯不同，導致基站信號的強弱等不同，從而每個測量值通常具有不同的測量誤差方差，故上述GDOP求解方法中的假設(3)不再適用。

2.2 加權幾何精度因子(WGDOP)

在一些同類型星座或組合星座組成的定位系統中，計算幾何精度因子時應用較多的方法是假設所有星座測得的偽距測量誤差是相互獨立且相等的擁有零均值的均方根值。然而實際中，每一時刻不同星座具有不同的偽距測量誤差，參考文獻[6]中針對該實際情況提出，在對組合定位系統進行定位精度評價誤差時使用加權幾何精度因子進行評價的觀點，但是對單一定位系統并沒有提出使用該方法的必要性，并且文中加權幾何精度因子的使用需以已知每一星座偽距測量誤差和星座幾何布局為前提。

地基導航系統由于其自身特殊的布設位置及信號特性，需要在定位之前通過使用合適的評價方法，選擇最優的布局方案對系統基站進行位置擺放，此時，要在不能獲得各基站偽距測量誤差的前提下得到加權幾何精度因子的表達式。加權幾何精度因子的本質在于通過給予每個測量誤差方差不同的權重分配，來削弱誤差大的結果對系統的影響。

假設：1)各站測量誤差為相同正態分布，且均值為0，方差相等；2)不同站間測量誤差互不相關。則n基站的測距誤差協方差矩陣為：

(8)

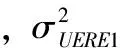
(9)

通過上述公式推導，得出WGDOP矩陣表達式為：

(10)

為了更好地提高地基導航系統定位精度，需要找到使得WGDOP最小的布局方案，若想使用WGDOP代替GDOP值來進行定位精度評價，需要對系統測量誤差進行觀測量建模，從而得到加權幾何精度因子表達式當中的加權矩陣Wn。

2.3 偽距誤差及加權矩陣計算

根據2.2節對WGDOP表達式的推導，使用加權精度因子對系統進行評價的前提是獲得加權矩陣Wn，而Wn只與地基導航系統偽距測量誤差有關。

2.3.1 偽距測量誤差

地基導航系統偽距包括各種測量誤差，按照其來源不同可主要分為以下幾個方面:1)與基站有關的誤差：站間時間同步時鐘誤差；2)與信號傳播有關的誤差：大氣層延遲誤差，由于地基導航系統信號不通過電離層，因此只有對流層延時誤差；3)與接收機有關的誤差：接收機由于地點的不同，會受到不同程度的多路徑效應及電磁干擾，同時還包括接收機自身噪聲。

由于地基導航系統通過基于雙向測距的時間同步方法，可實現優于1ns的時間同步精度，因此可忽略時間同步時鐘誤差帶來的影響。通過對地基導航系統模型進行大氣延時誤差修正以及慎重選擇基站布設位置后，偽距測量誤差將主要取決于接收機自身噪聲誤差。

2.3.2 接收機噪聲均方差σtDLL表達式

在不考慮上述其他干擾的情況下，接收機偽距測量誤差源主要包括由熱噪聲所致的碼相位抖動和動態應力誤差兩部分。接收機熱噪聲主要指天線、放大器和各部分電子器件的熱噪聲、衛星間的互相關性等，其噪聲具有隨機性。根據相干點積功率法，可得接收機噪聲均方差表達式為：

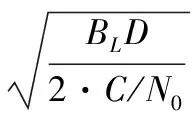
(11)

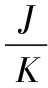
從而，近似得到各個基站測量誤差方差表達式為：

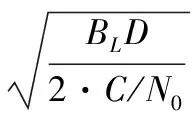
(12)

2.3.3 加權矩陣Wn

由自由空間傳播損耗公式可知：

(13)

根據變量值的大小，對比例進行等式近似，得:

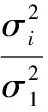
(14)

從而得到加權矩陣Wn的表達式為：

(15)

3 計算機仿真

3.1 GDOP布局評價法

針對四基站情況進行仿真，選取4個基站坐標分別為A1(0，0，1)，A2(√3，1，0.5)，A3(-√3，1，0.6)，A4(0，-2，0.7)，單位為km，四基站位置如圖2所示，選取地面一點作為用戶位置，高度為0 km，同時以0.01 km的步進值使用GDOP法對該布局進行定位精度評價，結果如圖3所示。

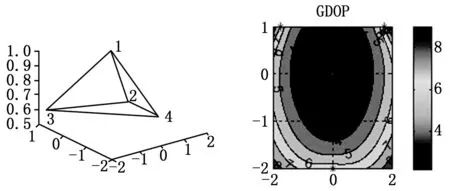
圖2 基站位置 圖3 GDOP值

針對上述布局方案，分別統計區域內GDOP值小于3、4、5、6的區域所占總面積的百分比，結果如表1所示。從表中可得，當按照傳統GDOP對該定位布局進行評價時，顯示會有46.9%的待定位區域可達到GDOP值小于4，最小值可達2.2142，然而該評價方法并未考慮到基站與用戶的距離對定位精度的影響。

表1 GDOP覆蓋范圍

3.2 WGDOP布局評價法

3.2.1 主基站的選取

公式(10)WGDOP算法需要確定一個主基站，從而得到與該主基站有關的加權矩陣。為了探討主基站的位置，對以下幾種四基站情況進行仿真。

如圖2，用戶位于地面，高度為0，以0.01的步進值，分別選取4個基站作為主基站進行實驗仿真，結果如圖4所示。

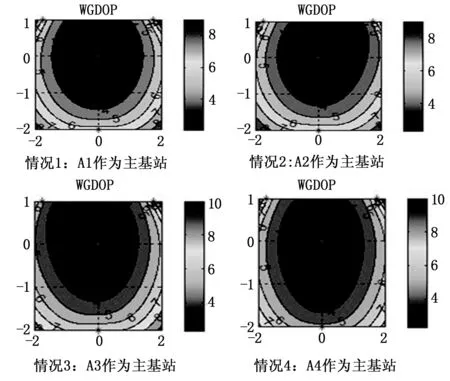
圖4 4種情況下WGDOP分布圖

仿真結果顯示，當以區域中心處基站作為主基站時，區域精度因子相對較好，因此選取布設在區域中心附近的基站(如上例中A1站)為主基站。更多基站布局時，仍按該原則選取主基站位置。

3.2.2WGDOP仿真結果

針對將A1作為主基站方案，分別統計區域內WGDOP值小于3、4、5、6的區域所占比例，如表2所示，故知，當按照WGDOP對該定位布局進行評價時，中心區域的精度因子值變化較大，低值覆蓋區域面積增加。對于外圍精度因子較大區域，并無太大區別，相較于GDOP評價方法，該評價方法特點在于考慮到基站與用戶的距離對定位精度的影響。

表2 WGDOP覆蓋范圍

3.3 定位仿真實驗

針對前文基站布局，對系統加入測量誤差，測量誤差方差為0.0087，定位解算結果為(1.1639，0.0084，-0.1705)，實際位置為(1，0，0)，定位誤差方差為0.0187，該點GDOP=2.2142，WGDOP=2.1705，經仿真驗證，測量誤差方差乘以WGDOP的值更接近于真實定位誤差方差。

3.4GDOP與WGDOP仿真結果對比分析與結論

在上述布局方案下，選取用戶活動范圍內的四點位置，分別使用兩種評價方法對其進行評價，結果如表3。

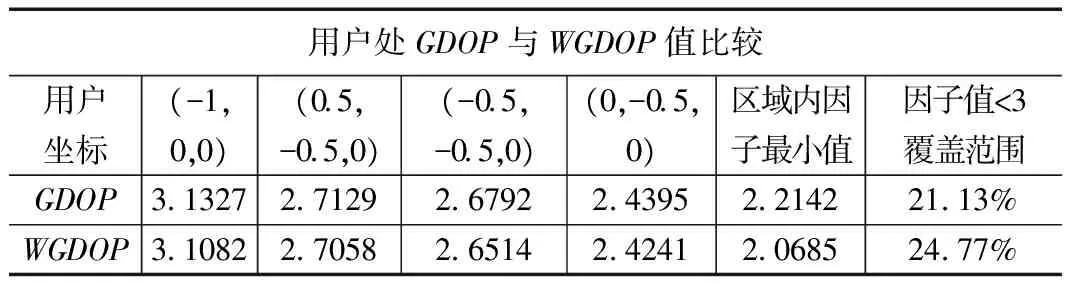
表3 GDOP與WGDOP定點值比較

實驗2.3得出，使用WGDOP對系統定位進行評價，更加符合實際定位結果，評判更加合理。綜合表1、2、3，該定位布局中心區域的WGDOP計算的高精度因子(<3)覆蓋比GDOP多出3.64%,存在顯著差別，值相較于GDOP值變化較大。在區域內定點精度分析上，根據實際情況中，進行定位時，不希望大誤差測量值對結果有較大影響，故對各站測量誤差進行權重分配，減小大測量誤差權重，使得WGDOP值應小于該點GDOP值，實驗結果表明該理論分析正確，因此可以得到WGDOP權重分配與用戶到基站距離的相關性：對于與用戶距離小的基站測量誤差方差，加權矩陣給予大權重，而對于與用戶距離大的基站測量誤差方差，則給予小權重。相較于GDOP評價方法，該評價方法最大的特點就是考慮到根據基站與用戶的距離對測量誤差方差進行權重分配，從而使評價標準更加貼合實際情況，為基站布局提供更準確的評價準則。因此，采用WGDOP進行布局評價更加合理。

4 總結

在地基導航系統中，由于基站到用戶距離差異很大，導致基站所產生的測量誤差不同，因此在對定位誤差進行分析時，應考慮距離因素，而加權幾何精度因子(WGDOP)相較于傳統幾何精度因子，選取了與距離相關的加權矩陣作為新的衡量標準，從分析地基導航系統誤差方差入手，對WGDOP表達式進行詳細分析，通過系統比較兩種定位因子，得出在中心區域距離主基站相對近的區域，WGDOP與GDOP有明顯差異，說明采用WGDOP作為地基導航系統基站布設評價標準,可以更直觀的表示出精度因子與用戶距基站距離之間的相關性，準確性高、更加貼合實際情況。研究結果表明，采用加權幾何精度因子作為評價標準，可以更加符合地基導航系統的實際使用環境，并且可以提高精度評價的準確性。

[1] 何秀鳳，桑文剛，楊 光.偽衛星增強GPS精密定位新方法[J].東南大學學報：自然科學版，2005,35(5): 460-464.

[2] 王暉輝，李 實，王 輝,等.地面偽衛星測試環境中關于精度因子的仿真研究[J]．測繪通報，2009，8：6-9.

[3] 彭瑞雪，胥 霖，王 富．偽衛星定位系統中組網布局研究[J]．兵工自動化，2010，29(8)：53-56.

[4] Guo X, Zhou Y, Yang J. Research on Time Synchronization Method of Ground-Based Navigation System[A].CSNC 2015 Proceedings: Volume I. Lecture Notes in Electrical Engineering[C].Springer Berlin Heidelberg, 2015, 340:529-536.

[5] 宋 倩，張 波，李署堅.地面偽衛星組網布設技術研究[J].計算機測量與控制，2013，21(3)：199-202.

[6] Chen C S. Weighted geometric dilution of precision calculations with matrix multiplication[J].Sensors, 2015, 15, 803-817.

EvaluatingFoundationsNavigationSystemBasedonWeightedGeometricDilutionofPrecision

Yang Nan1, Li Hao2, Liu Kai1, Liu Changshui1

(1.School of Electronic Science and Engineering, National University of Defence Technology, Changsha 410073, China;2.Army Aviation Military Representative Office, Beijing 100101,China)

In order to evaluate the performance of position estimation in satellite navigation systems, GDOP is widely used as an evaluation method to measure the geometric relationship between measurement error and positioning error. Because the measurement error of each unit of the foundation navigation system is different and the influence of the user distance is not negligible, it is necessary to study the distance-related evaluation standard. Therefore, it is proposed to use WGDOP instead of GDOP as the criterion, and from the analysis of the variance of the foundation navigation system error, the WGDOP expression is analyzed in detail. By comparing the two positioning factors, the WGDOP is used as the foundation navigation system base station to set the evaluation standard and improve the accuracy. The results show that the weighted geometric accuracy factor can be used as the criterion to evaluate the actual use environment of the foundation navigation system, and the accuracy of the system positioning performance is improved.

foundations navigation system; WGDOP; GDOP

2017-04-10；

2017-06-01。

楊 楠(1992-)，女，天津市人，碩士研究生，主要從事地基導航基站布局方向的研究。

1671-4598(2017)10-0293-04

10.16526/j.cnki.11-4762/tp.2017.10.075

TP273

A