輪式機器人軌跡跟蹤控制系統的設計

，,2，

(1.蘭州理工大學 機電工程學院，蘭州 730050；2.蘭州理工大學 數字制造技術與應用教育部重點實驗室，蘭州 730050)

輪式機器人軌跡跟蹤控制系統的設計

王猛1，靳伍銀1,2，王安1

(1.蘭州理工大學機電工程學院，蘭州730050；2.蘭州理工大學數字制造技術與應用教育部重點實驗室，蘭州730050)

針對輪式機器人軌跡跟蹤控制系統誤差收斂速率低、精度和實時性差的問題，采用反演控制算法并結合李雅普諾夫穩定性分析方法對輪式機器人的軌跡跟蹤系統進行了優化設計;建立了輪式機器人軌跡跟蹤控制系統的運動學模型，并對該模型進行位置偏差分析；在反演控制算法中引入了分部虛擬控制量，并分析和設計了其他間接受控量，提高了算法運行的效率；采用李雅普諾夫收斂定理對系統的收斂性進行分析，根據分析的結果提出了算法更加簡單的控制律;利用Matlab軟件的Simulink庫對設計的軌跡跟蹤控制系統試驗研究;結果表明，與基于李雅普諾夫直接法或者迭代學習算法設計的輪式機器人軌跡跟蹤控制系統相比較，設計的控制系統具有跟蹤精度高、收斂速度快、實時性好的優點。

軌跡跟蹤；誤差分析；反演控制算法；李雅普諾夫收斂定理；分部虛擬控制量

0 引言

智能輪式機器人是一種在復雜的環境下工作的具有自規劃、自組織、自適應能力的機器人[1-4]。在移動機器人相關技術研究中，控制技術是其核心技術，也是其實現真正智能化和完全自主移動的關鍵技術[1]。輪式機器人具有時變、強耦合和非線性特性，由于測量和建模的不精確，加上負載的變化以及外部擾動的影響，傳統的基于經典控制理論的控制算法很難實現對輪式機器人的實時、精確控制[5-9]。目前，在輪式機器人軌跡跟蹤控制系統的設計中，常采用的算法有模糊PID控制算法、迭代學習控制算法和李雅普諾夫(Lyapunov)直接算法[10-14]，但是，模糊PID控制算法需要大量的專家經驗才能設計精確地控制規則，這在現實中是很難實現的；雖然采用迭代學習控制算法和李雅普諾夫直接法設計的機器人軌跡跟蹤控制系統基本上能夠滿足系統的穩定性和準確性要求，但是，由于迭代學習算法在控制過程中需要反復迭代，且迭代的次數與精度均沒有合理、系統的理論體系支撐，需要通過試驗反復迭代驗證，這嚴重影響了機器人控制系統的實時性要求；而Lyapunov直接法仍然沒有系統的、普遍適用的構造Lyapunov函數的方法，且收斂速度慢的缺陷。

本文采用反演(Backstepping)控制算法對輪式機器人軌跡跟蹤控制系統進行優化設計，建立了輪式機器人的運動學模型，對該模型進行誤差分析并引入分部虛擬控制量，并利用Lyapunov收斂定理分析了系統的收斂性，根據分析結果提出了一套算法簡單的控制律。最后采用Matlab/Simulink對控制系統進行試驗，結果表明本文采取的控制策略提高了系統的實時性、收斂精度和速率。

1 輪式機器人運動學模型

本文的研究對象為同軸雙電機差速轉向的輪式機器人，其位姿如圖1所示。

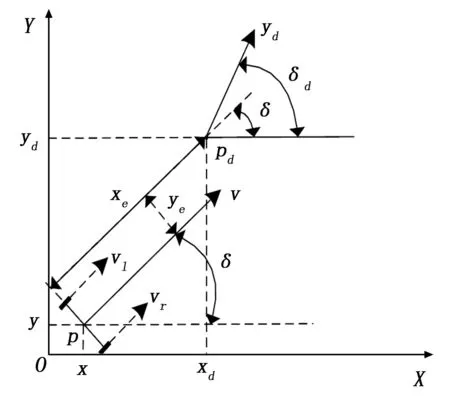
圖1 移動機器人位姿誤差坐標圖

圖1中，以機器人的兩驅動輪軸線中點為參考點對機器人位姿變化進行研究，其中p(x,y,δ)為機器人當前位姿，pd(xd,yd,δd) 為期望位姿，(x,y)為機器人的當前位置坐標，δ為機器人的當前行駛方向角，vl、vr分別為機器人的左、右輪線速度，v為機器人當前的速度，三者之間的近似關系如式(1)所示：

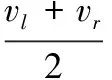
(1)

機器人在X、Y方向的位移變化以及角度變化如式(2)所示：

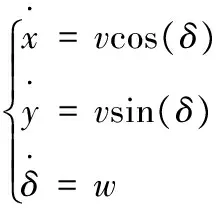
(2)

其中：w是機器人的角速度。

由式(2)可以看出，機器人的位姿狀態是由線速度v和角速度w決定的。

通過對圖1進行分析可得：

(3)

聯立式(2)、(3)可得：

(vdcos(δd)-vcos(δ))cos(δ)-(xd-x)wsin(δ)+

(vdsin(δd-vsin(δ))sin(δ)+(yd-y)wcos(δ)=

vdcos(δd)cos(δ)+vdsin(δd)sin(δ)-vcos2(δ)-vsin2(δ)+

w((yd-y)cos(δ)-(xd-x)sin(δ))=vdcos(δd-δ)-v+

yew=vdcos(δe)-v+yew

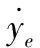
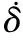
(yd-y)wsin(δ)-(vdcos(δd)-vcos(δ))sin(δ)-

(xd-x)wcos(δ)=vdsin(δd)cos(δ)-vdcos(δd)sin(δ)-

vsin(δ)cos(δ)+vsin(δ)cos(δ)-w((xd-x)cos(δ)+

(yd-y)sin(δ)=vdsin(δd-δ)-xew=vdsin(δe)-xew

即：

(4)

由式(4)可知，求解輪式機器人的尋跡問題就是設計適當的有界控制量q=(vw)T，使得機器人在任意初始條件下跟蹤參考軌跡pd=(xd,yd,δd)和參考控制量qd=(vdwd),使得xe,ye,δe,最終收斂于0。

2 反演控制算法設計

反演(Backstepping)控制算法設計的基本思想是將復雜的非線性系統分解成不超過系統階數的子系統，然后為每個子系統分別設計Lyapunov函數和中間虛擬控制量，一直“后退”到整個系統，直到完成整個控制律的設計[1,15-16]。Backstepping控制算法具有以下幾點優點：一是反向遞推設計，使系統的Lyapunov函數和控制器設計具有了相對系統化和結構化的過程；二是可以不受制于經典無源設計中相對階只能為1的要求，而對相對階為n的非線性系統也適用[17]。

2.1 反演控制算法設計

針對機器人位姿誤差變化中X方向的誤差分量構造虛擬控制量：

(5)

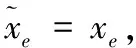
(6)

2.2 控制律設計與Lyapunov穩定性分析

設計系統的部分Lyapunov函數為：

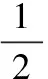
(7)

b2>0，于是：

(8)

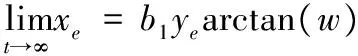
綜合以上對系統的分析設計控制系統的Lyapunov函數為：

(9)

于是得：

b1vdsin(δe)arctan(w) +b1xewarctan(w)]-

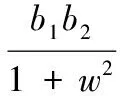
(10)

其中:h>0，b3>0。

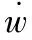
(11)

將式(11)代入式(10)可得：

(12)

由于?t∈[0,+∞)，xe，ye，δe有界，因此V函數是正定連續可微分的有界函數，于是系統是漸進穩定的。

3 仿真試驗與分析

利用Matlab軟件的Simulink庫對本文設計的輪式機器人軌跡跟蹤控制系統進行仿真試驗，利用式(2)、(4)、(6)和(12)設計控制系統的Matlab/Simulink仿真系統，如圖2所示。設定xd=cos(πt)，yd=sin(πt)，vd=0.2 m/s，wd=0.2 rad/s并取b1=0.08。即預定軌跡為一個單位圓。假設輪式機器人的初始位姿為(1.2 -0.3 2π/3)。

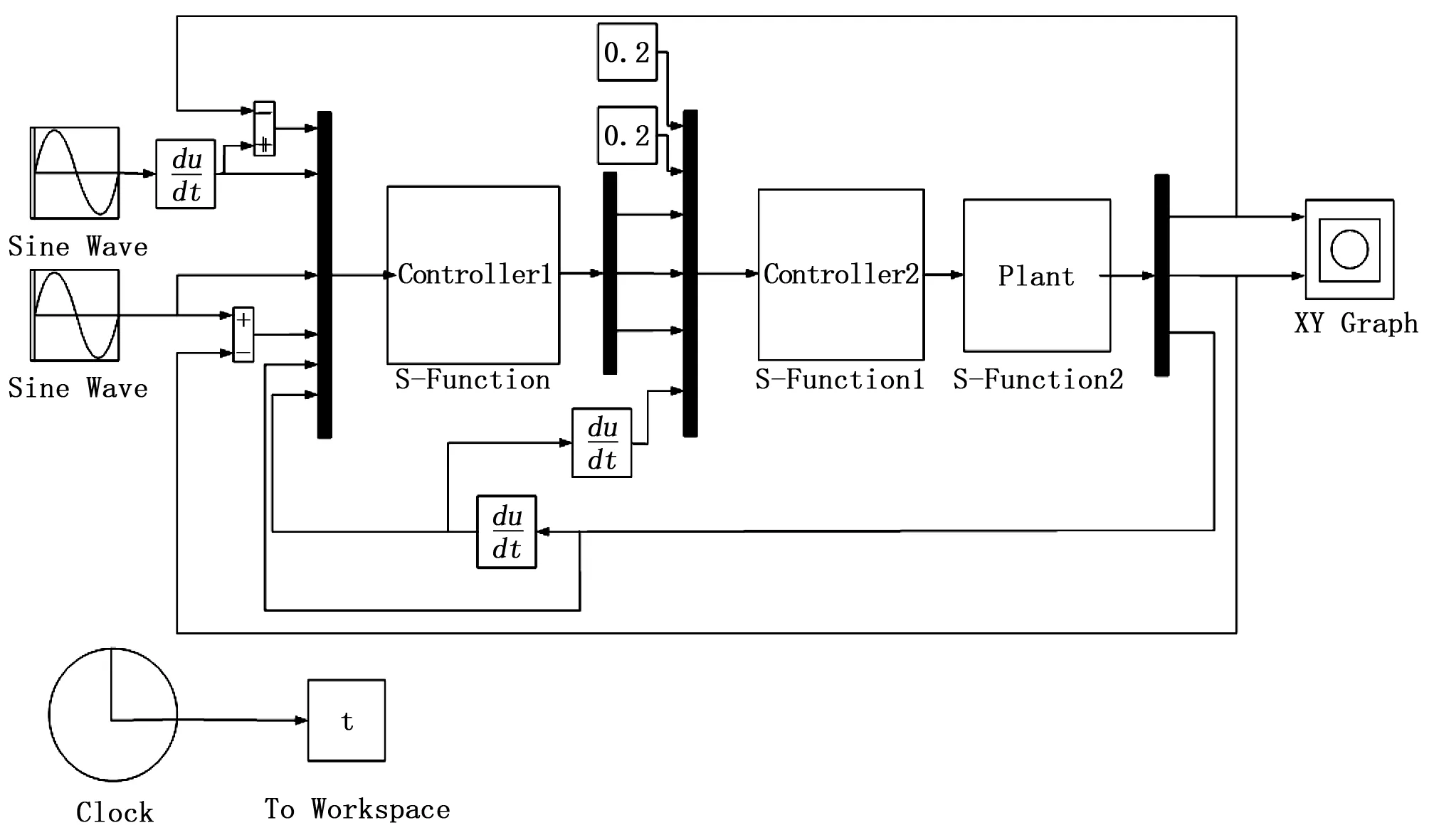
圖2 控制系統的Matlab/Simulink仿真結構圖

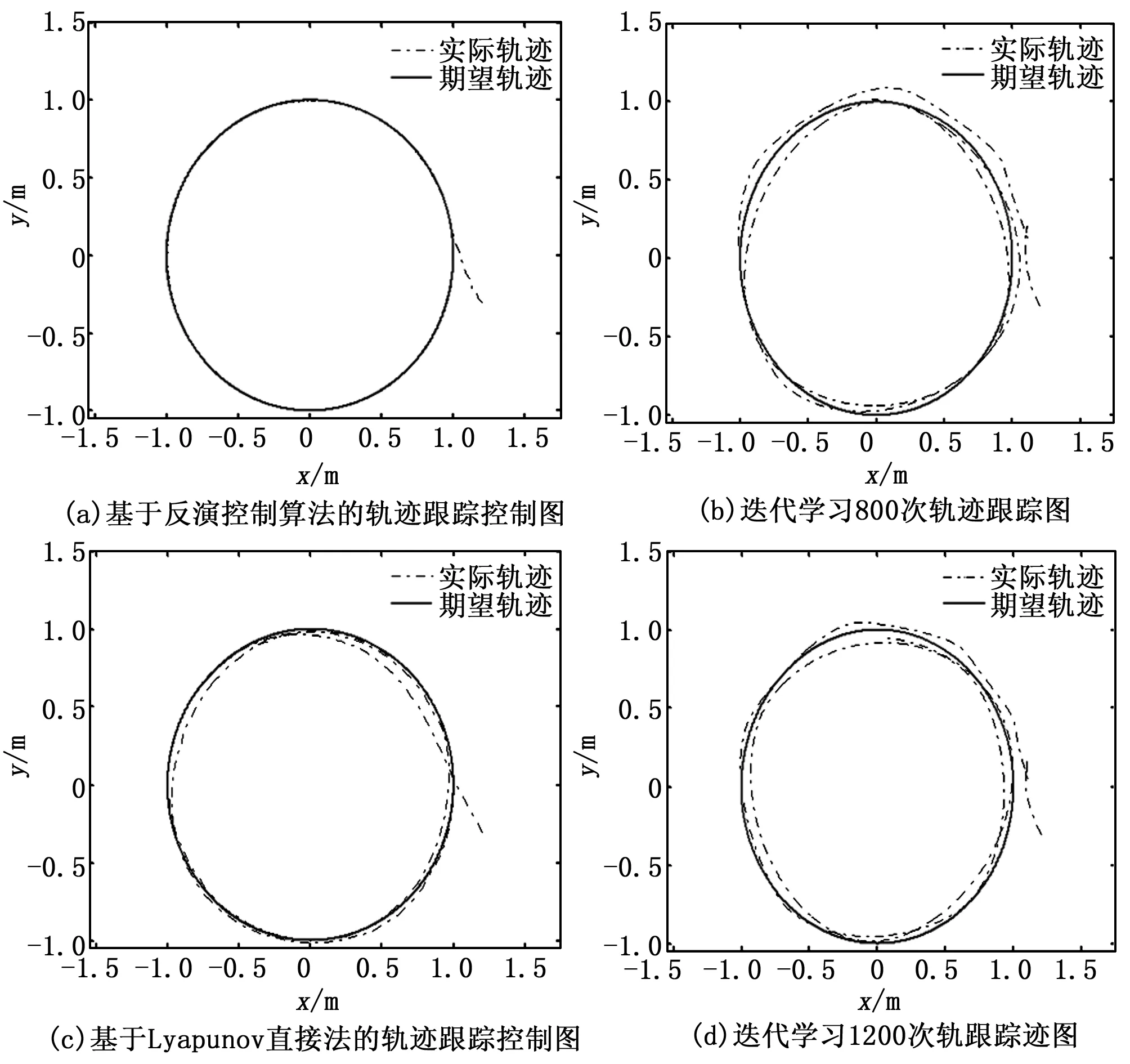
圖3 控制系統的仿真結果

控制系統的仿真結果如圖3所示，其中圖3(a)為本文設計的控制系統仿真結果，圖3(b)為采用迭代學習算法設計輪式機器人軌跡跟蹤系統在迭代學習800次仿真結果；圖3(c)為基于Lyapunov直接法設計的控制系統仿真結果，由圖3(d)可為采用迭代學習算法設計輪式機器人軌跡跟蹤系統在迭代學習1200次的仿真結果。對比圖3(a)，(b)和圖3(c)可知，與基于Lyapunov直接法設計的控制系統和基于迭代學習算法設計的控制系統相比，本文優化設計的軌跡跟蹤控制系統具有更好的跟蹤精度和收斂速率。對比圖3(b)和圖3(d)可知，采用迭代學習算法設計的控制系統的跟蹤精度與迭代的次數有關。對仿真試驗的結果進行分析，結果表明：本文優化設計的軌跡跟蹤控制系統跟蹤預定軌跡的效率和精度要高于基于Lyapunov直接法和基于迭代學習控制算法設計的控制系統，同時也證明了本文引入的虛擬控制量以及設計的控制律具有很好的收斂效果，實現了輪式機器人軌跡跟蹤控制的目標。

4 結論

本文基于反演算法對輪式機器人軌跡跟蹤控制系統進行了優化設計，建立了輪式機器人的運動學模型，對模型進行位置偏差分析，為了提高算法的效率，在反演控制算法中引入了分部虛擬控制量，利用分部虛擬控制量來分析和設計其他間接受控量，采用李雅普諾夫收斂定理對系統的收斂性進行分析，并根據分析的結果提出了算法更加簡單的控制律。最后對優化設計的控制系統進行了仿真試驗，結果表明：與采用李雅普諾夫直接法或者迭代學習算法設計的控制系統相比較，本文優化設計的控制系統具有跟高的跟蹤精度、更高的收斂速率，更好的實時控制性能。

[1]宋永端. 移動機器人及其自主化技術[M]. 北京:機械工業出版社, 2012.

[2]劉起興, 吳欽木. 四輪移動機器人控制系統的設計[J]. 東北師大學報(自然科學), 2016(3):74-78.

[3]Fauadi M H F B M, Jafar F A, Yee L O, et al. Modeling and path planning simulation of a robotic Arc welding system[J]. Lecture Notes in Electrical Engineering, 2014, 291:327-334.

[4]任紅格, 阮曉鋼. 基于Boltzamnn機的機器人自主學習算法[J]. 北京工業大學學報, 2012(1):60-64.

[5]Tao S, Hongge R, Rui Y, et al. Research on robust bionic learning algorithm in balance control for the robot[A].The 27th Chinese Control and Decision Conference (2015 CCDC)[C]. IEEE, 2015: 4387-4390.

[6]Sun W, Tang S, Gao H, et al. Two time-scale tracking control of nonholonomic wheeled mobile robots[J]. IEEE transactions on control systems technology, 2016:1-11.

[7]Xia D, Kong L, Hu Y, et al. Silicon microgyroscope temperature prediction and control system based on BP neural network and Fuzzy-PID control method[J]. Measurement Science & Technology, 2015, 26(2):38-42.

[8]Zhou M, Zhang Q. Hysteresis model of magnetically controlled shape memory alloy based on a PID neural network[J]. IEEE Transactions on Magnetics, 2015, 51(11):1-4.

[9]Zhao J, Han L, Ren S. RBF neural network adaptive sliding mode control based on genetic algorithm optimization[A]. Chinese Control and Decision Conference[C]. 2016.

[10]曹玉麗, 史儀凱, 袁小慶,等. 自平衡機器人變論域模糊PID控制研究[J]. 計算機仿真, 2013, 30(2):347-350.

[11]Wang W, Chen J, Mao L. Two-wheeled mobile robot tracking based on iterative learning control[A].Advanced Materials Research. Trans Tech Publications[C]. 2012, 433: 5866-5870.

[12]裴九芳, 王 海, 許德章. 基于迭代學習控制的移動機器人軌跡跟蹤控制[J]. 計算機工程與應用, 2012, 48(9):222-225.

[13]陳 梅, 陳艷燕. 兩輪智能車跟蹤控制系統的研究[J]. 合肥工業大學學報自然科學版, 2015(3):319-324.

[14]Kausar Z, Stol K, Patel N. Nonlinear control design using Lyapunov function for two-wheeled mobile robots[A].Mechatronics and Machine Vision in Practice (M2VIP), 2012 19th International Conference[C]. IEEE, 2012: 123-128.

[15]Furtat I B, Tupichin E A. Modified backstepping algorithm for nonlinear systems[J]. Automation & Remote Control, 2016, 77(9):1567-1578.

[16]Azimi M M, Koofigar H R. Adaptive fuzzy backstepping controller design for uncertain underactuated robotic systems[J]. Nonlinear Dynamics, 2015, 79(2):1457-1468.

[17]楊 敏. 輪式移動機器人控制算法研究及其伺服系統設計[D]. 南京航空航天大學, 2014.

[18]閔穎穎, 劉允剛. Barbalat引理及其在系統穩定性分析中的應用[J]. 山東大學學報: 工學版, 2007, 37(1): 51-55.

DesignofTrajectoryTrackingControlSystemforWheeledRobots

Wang Meng1，JIN Wuyin1,2， Wang An1

(1.School of Mechanical and Electrical Engineering, Lanzhou University of Technology, Lanzhou 730050, China；2.Key Laboratory of Digital Manufacturing Technology and Applications(Lanzhou University of Technology), Ministry of Education, Lanzhou 730050, China)

Aim at the shortages of slow error convergence speed, low accuracy, and poor real-time ability of trajectory tracking control system for wheeled robots, a novel control system is proposed based on Backsteping control algorithm and Lyapunov stability analysis method. In order to study the position deviation of the wheeled robots, the kinematic model is designed. In addition, the Backstepping control algorithm employ a new control strategy for segment virtual control to study and design other indirectly controlled parameters, which greatly improves the efficiency of the algorithm. The Lyapunov law is adopted to analyze the convergence of the system, and in the light of the results of stability analysis to propose a new and simple control law. Finally, Matlab/Simulink is employed to test trajectory tracking control system. The results show that the new control strategy proposed in this paper has higher accuracy, faster convergence speed and better real-time performance than the control strategy based on direct Lyapunov algorithm or iterative learning algorithm.

trajectory tracking; error analysis; backstepping algorithm; lyapunov convergence law; segment virtual control

2017-03-19；

2017-04-23。

2016年度省自然基金B類項目：刀具熱變形因素對切削系統穩定性的影響。

王 猛(1992-)，男，河南商丘人，碩士研究生，主要從事嵌入式智能系統方向的研究。

靳伍銀(1969-)，男，甘肅秦安人，博士，研究員，博導，主要從事機器視覺與嵌入式系統方向的研究。

王 安(1981-)，男，甘肅靖遠人，博士研究生，講師，主要從事非線性系統方向的研究。

1671-4598(2017)10-0102-03

10.16526/j.cnki.11-4762/tp.2017.10.027

TP391

A