一類基于波利亞分布的修正的Lupas-Durrmeyer型算子

連博勇, 蔡清波

(1.仰恩大學數學系,福建 泉州 362014;2.泉州師范學院數學與計算機科學學院,福建 泉州 362000)

一類基于波利亞分布的修正的Lupas-Durrmeyer型算子

連博勇1, 蔡清波2

(1.仰恩大學數學系,福建 泉州 362014;2.泉州師范學院數學與計算機科學學院,福建 泉州 362000)

引入了一類基于波利亞分布的修正Lupas-Durrmeyer型算子,它具有常數保持與線性保持性質.利用連續模,光滑模,K-泛函,Lipschitz函數類,討論了該算子的某些逼近性質,在區間上該算子具有更好的收斂結果.最后還給出了該算子的Voronvskaya型漸近展開公式.

Lupas-Durrmeyer型算子;K-泛函;光滑模;Voronvskaya型漸近展開公式

1 引言

Aral等在文獻[1]中定義了一類Lupas-Durrmeyer型算子:

這里f∈C[0,1],

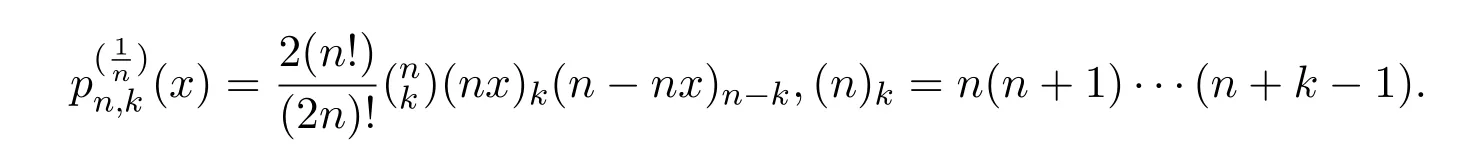
其中

最近,在文獻[1]的基礎上Gupta[2]引入了另一類Lupas-Durrmeyer型算子,

自2003年King[6]引入修正的Bernstein算子以來，近十多年來修正型的算子成為逼近論領域的一個研究熱點.在這些研究中,有關于算子線性保持的[7-8],有關于算子平方保持的[6,9],甚至推廣到修正的q算子中[10-11].

設

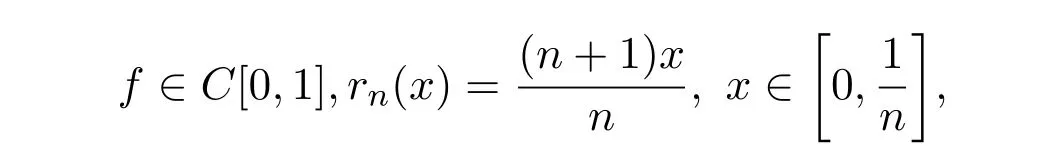
定義

首先給出一些基本定義.

設

定義:

一階連續模

二階光滑模

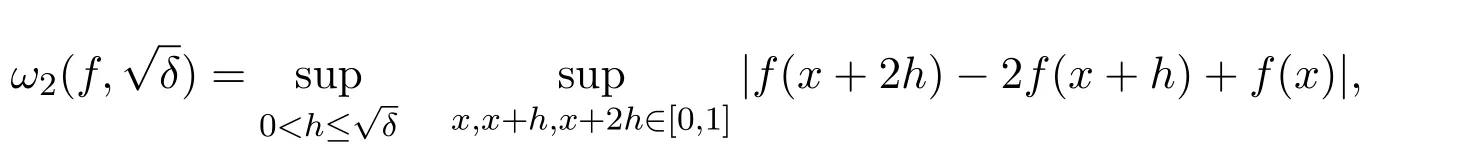
對應的K-泛函是

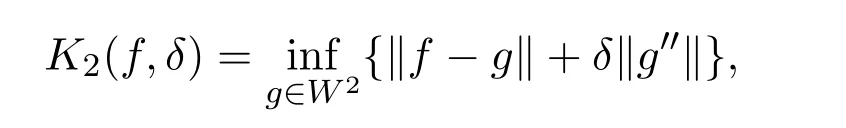
其中

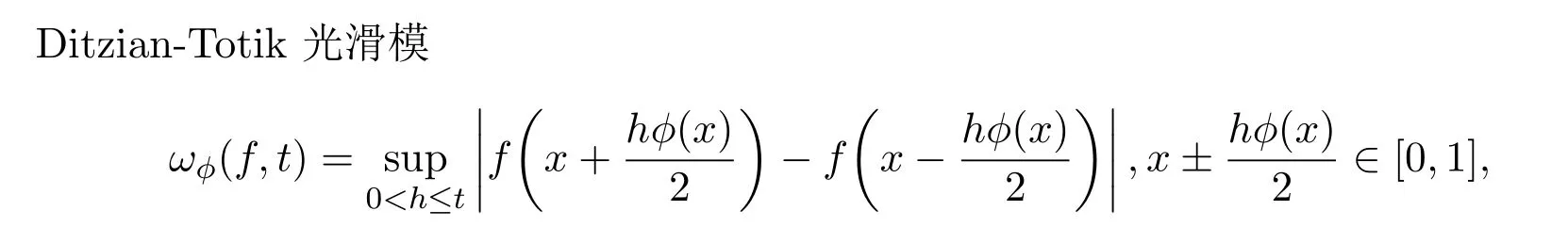
對應的K-泛函是

其中

AC[0,1]表示區間[0,1]上的絕對連續函數.Lipschitz函數類

其中

2 若干引理

為了得到算子的逼近性質,需要如下引理:

引理2.1[2]令ei=ti,i=0,1,2,有

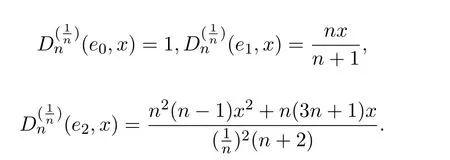
注2.1由引理2.1,得

類似于引理2.1的計算方法,可以得到

引理2.2令時,有

注 2.2由引理2.2,得

即

注2.3經過簡單的計算,有

注2.4由遞推關系,得

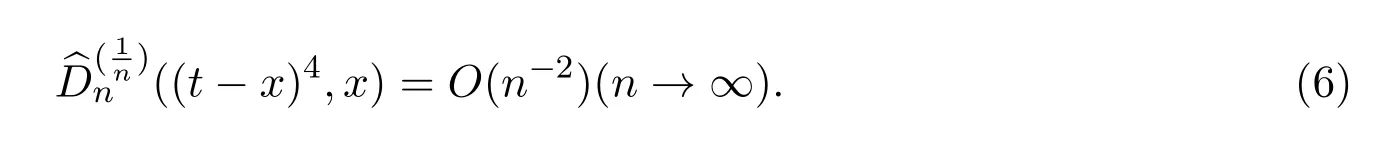
引理2.3設f∈C[0,1],當時,有

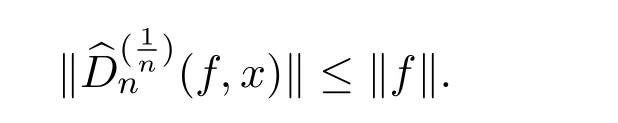
證明由算子的定義及引理2.2,得

引理2.4[13]設f(x)∈C[0,1],則存在常數C＞0,使得

引理 2.5[14]設f(x)∈C[0,1],則存在常數C＞0,使得

3 主要結果

定理3.1設f∈C[0,1],當時,有

證明由引理2.2,可得

應用Korovkin定理,即得定理3.1.

定理3.2設f∈C[0,1],則當時,有

證明由的單調性可知,對任意的λ＞0,有

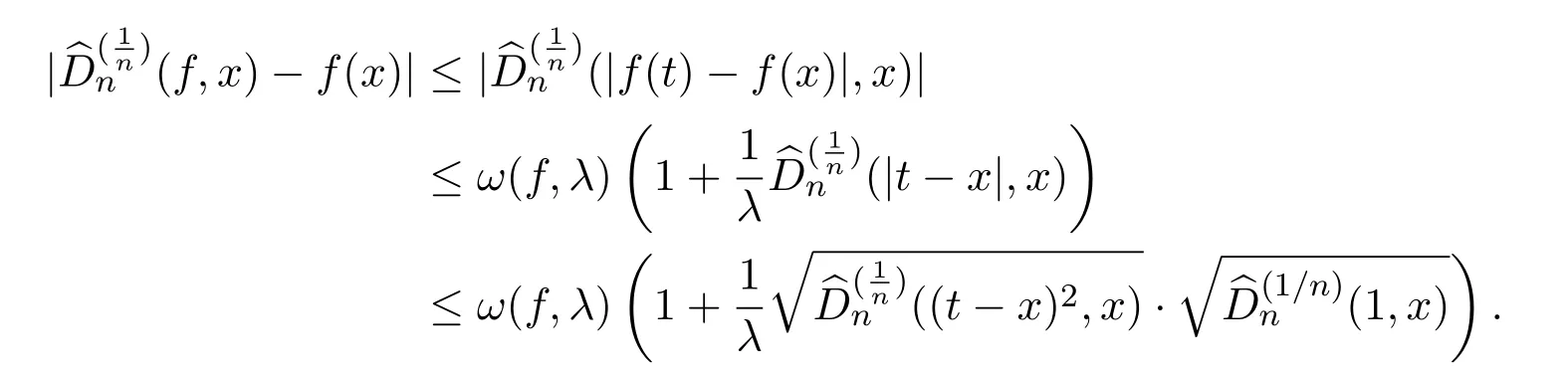
取

結合引理2.2及注2.3,可得定理3.2.

定理 3.3設f∈C[0,1],則當時,存在常數C＞0,使得

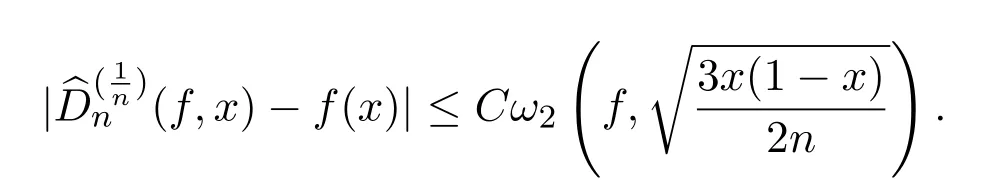
證明令g∈W2,由Taylor展開式,得

根據引理2.2,可知

從而有

所以

對所有的g∈W2,上式取下確界,得

由引理2.4,可得

定理3.4設f∈C[0,1],則當時,存在常數C＞0,使得

證明由Taylor展開式,得

因此

任意的x,t∈(0,1),有

且

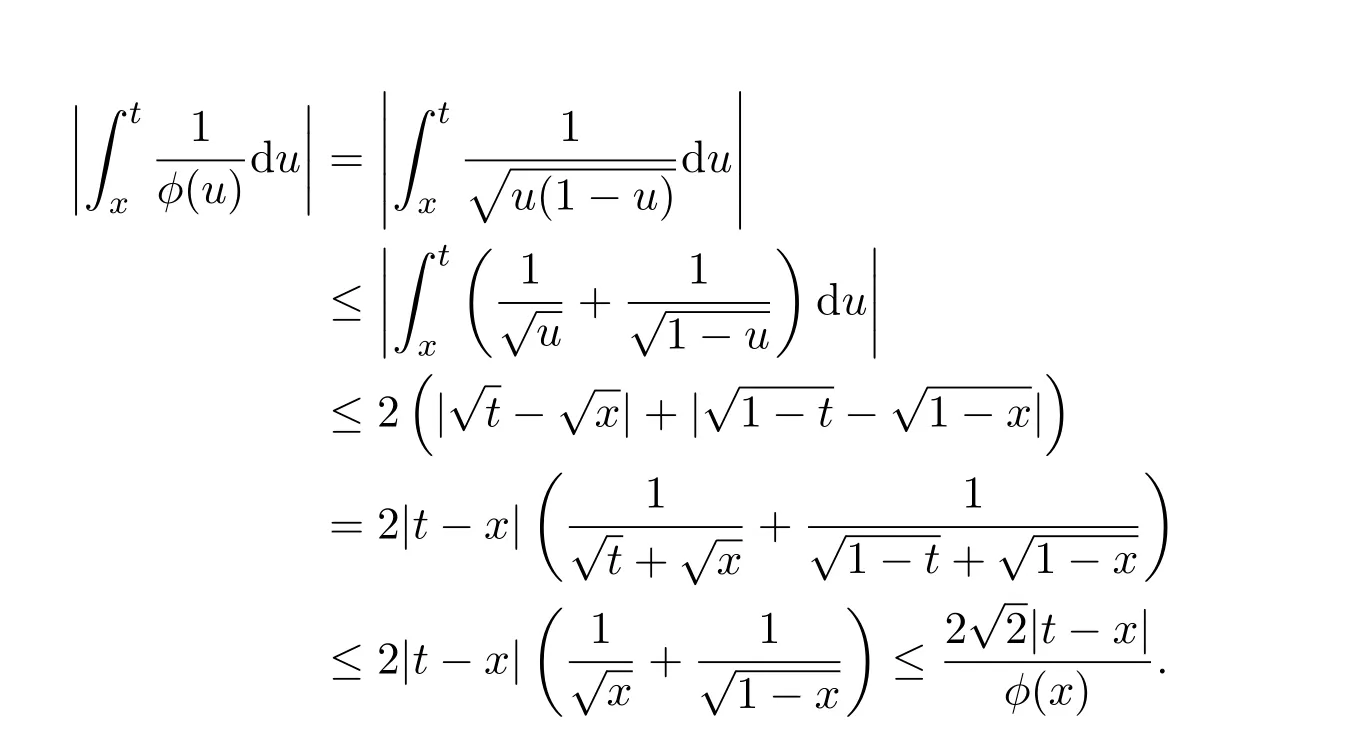
應用Cauchy-Schwarz不等式,得

從而有

對所有的g∈W?[0,1],上式取下確界,得

由引理2.5,立即得定理3.4.

定理 3.5設 f∈LipM(β),則當時,有

證明取

根據 H?lder不等式,引理 2.2及注 2.3,有

定理 3.6設時,有

證明由Taylor公式,得

其中 ?(t;x)是 Peano余項,滿足 ?(t;x)∈C[0,1],且從而有

由Cauchy-Schwartz不等式,得

注意到 ?2(x;x)=0及 ?2(t;x)∈C[0,1],由定理 3.1,得

由注2.2,(6),(10),(11),立即得到

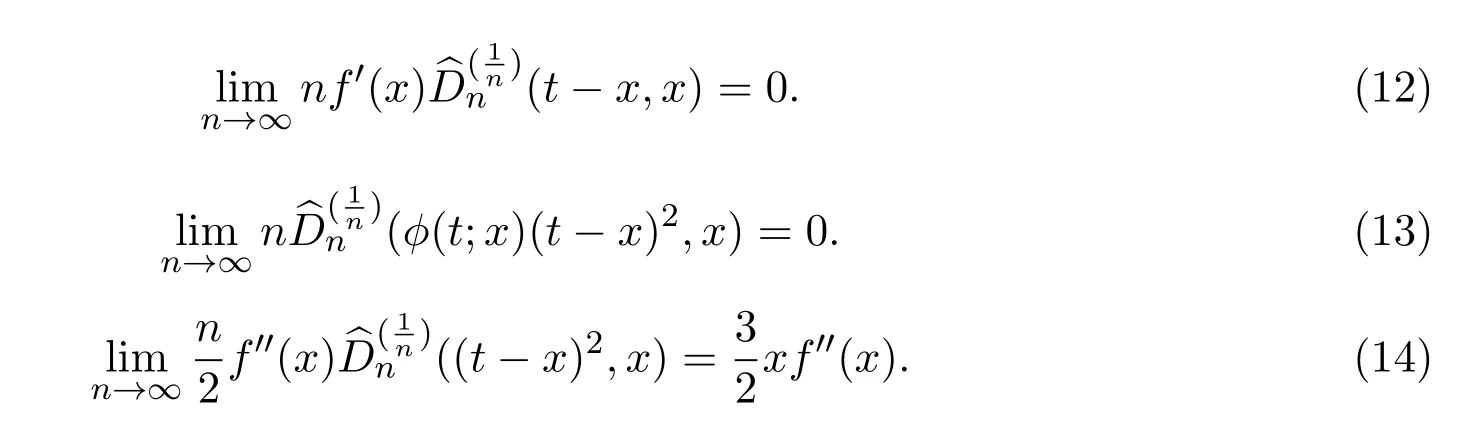
由(9)-(14)式得定理3.6.

[1]Aral A,Gupta V.Direct estimates for Lupas-Durrmeyer operators[J].Filomat,2016,30(1):191-199.

[2]Gupta V,Soybas D.Convergence of integral operators based on di ff erent distributions[J].Filomat,2016,30(8):2277-2287.

[3]Neer T,Acu A M,Agrawal P N.B′ezier variant of genuine-durrmeyer type operators based on polya distribution[J].Carpathian J.Math.,2016,33(1):73-86.

[4]Neer T,Agrawal P N.A genuine family of Bernstein–Durrmeyer type operators based on polya basis functions[J].Filomat,2017,31(9):2611-2623.

[5]Agrawal P N,Ispir N,Kajla A.Approximation properties of Lupas–Kantorovich operators based on polya distribution[J].Rendiconti del Circolo Matematico di Palermo Series 2,2016,65(2):185-208.

[6]King J P.Positive linear operators which preserve x2[J].Acta.Math.Hungar,2003,99(3):203-208.

[7]Duman O,Ozarslan M A,Vecchia B D.Modi fi ed Szasz-Mirakjan-Kantorovich operators preserving linear functions[J].Turkish J.Math.,2009,33(2):151-158.

[8]Deo N,Bhardwaj N.Some approximation results for Durrmeyer operators[J].Appl.Math.Comput.,2011,217(12):5531-5536.

[9]Rempulska L,Tomczak K.On approximation of functions by certain operators preserving x2[J].Comment.Math.Univ.Carolin,2008,49(4):579-593.

[10]Aral A,Gupta V,Agarwal R P.Applications of q-Calculus in Operator Theory[M].New York:Springer,2013.

[11]蔡清波.一類修正的Durrmeyer型q-Baskakov算子的統計收斂性質[J].高校應用數學學報,2012,27(3):351-358.

[12]鄧雪莉,吳嘎日迪.關于 Bernstein-Durrmeyer-B′ezier算子在 Orlicz空間內的逼近 [J].純粹數學與應用數學,2015,31(3):307-317.

[13]Devore R A,Lorentz G G.Construtive Approximation[M].Berlin:Springer-Verlag,1993.

[14]Ditzian Z,Totik V.Moduli of Smoothness[M].New York:Springer-Verlag,1987.

Some modi fi ed Lupas-Durrmeyer type operators based on Polya distribution

Lian Boyong1,Cai Qingbo2
(1.Department of Mathematics,Yang′en University,Quanzhou 362014,China;2.School of Mathematics and Computer Science,Quanzhou Normal University,Quanzhou 362000,China)

In this paper,the authors introduce a class of modi fi ed Lupas-Durrmeyer type operators based on Polya distribution which preserve constant and linear functions.By using modulus of continuity,modulus of smooth,K-functional and Lipschitz class,the rate of convergence of these operators are derived.The modi fi ed Lupas-Durrmeyer type operators have better error estimatin on the intervalthan the classical Lupas-Durrmeyer type operators.Finally,the authors present a Voronovskaya-type asymptotic formula.

Lupas-Durrmeyer type operators,K-functional,modulus of smoothness,Voronovskaya-type asymptotic formula

O174.41

A

1008-5513(2017)05-0466-09

10.3969/j.issn.1008-5513.2017.05.004

2017-08-09.

國家自然科學基金(11601266);福建省自然科學基金(2016J05017);2016年福建省高校杰出青年科研人才培育計劃.

連博勇(1982-),碩士,副教授,研究方向:函數逼近論.

2010 MSC:41A25,41A35