(2+1)維廣義破裂孤子方程的非局域對稱及相互作用解
白喜瑞, 沃維豐
(寧波大學數學系,浙江 寧波 315211)
(2+1)維廣義破裂孤子方程的非局域對稱及相互作用解
白喜瑞, 沃維豐
(寧波大學數學系,浙江 寧波 315211)
根據截斷的Painlev′e分析展開法及相容Riccati展開 (CRE)法,研究了 (2+1)維廣義破裂孤子方程的非局域對稱.利用非局域對稱局域化的方法,得到了與Schwarzian變量相對應的對稱群.同時,證明了這個方程是CRE可積的,并給出了它的孤立波與橢圓周期波之間的相互作用解.
(2+1)維廣義破裂孤子方程;非局域對稱;CRE方法;相互作用解
1 引言
在過去的幾十年里,許多的非線性發展方程被發現,它們被用于研究復雜的物理現象.Painlev′e分析是研究這些方程的可積性的重要方法之一[12],并且它還可以用來構造方程的非局域對稱.在2013年,Lou等[34]通過截斷的Painlev′e展開法提出了留數對稱定理.由于留數對稱與初始非線性發展方程的Schwarzian形式有著密切的關系,因此它比Darboux變換,B?cklund變換更易于使這些方程局域化.迄今為止,構造非線性發展方程的精確解的方法已有很多種,例如反散射方法,Darboux變換方法,Hirota雙線性方法,對稱約化方法,函數展開法等.而非線性發展方程的相互作用解在數學物理中有著重要的應用并且很難構造,因此吸引了越來越多學者的研究.Lou[5]發現了相容Riccati展開(CRE)方法,這種方法不僅驗證了許多可積系統是CRE可解的[69],而且與其它方法相比,它對于構造不同類型的相互作用解也更為簡單,有效.(2+1)維廣義破裂孤子方程的一般形式為:
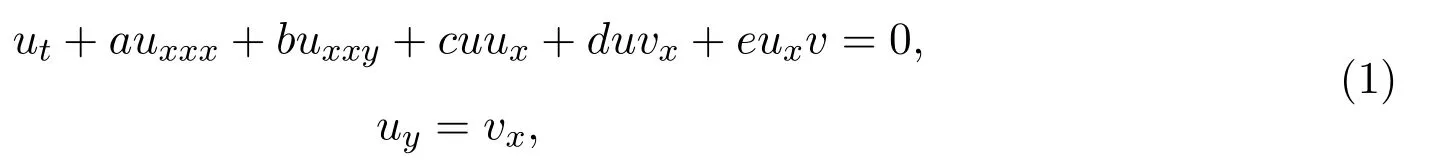
這里a,b,c,d,e都是任意實參數,下標表示求偏導.方程(1)描述了沿y軸傳播的Riemann波與沿x軸傳播的長波之間的交互作用.當a,b,c,d,e取某些特殊值時,方程(1)可轉化為某些特殊的方程.例如,令
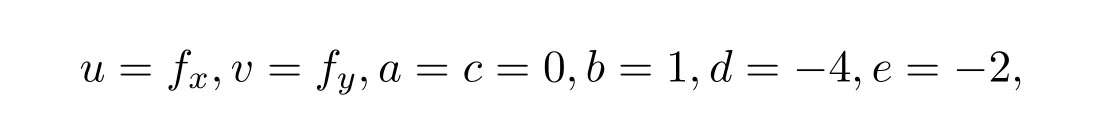
我們可得到破裂孤子方程[10-13]:
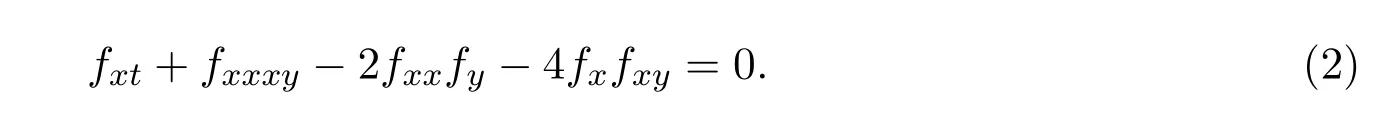
文獻[11-12]研究了(2)的非局域對稱與相互作用解.其它特殊情況可詳見文獻[14].在文獻[14]中,作者通過對方程 (1)進行 Painlev′e分析,得到了一個新的 (2+1)維的廣義破裂孤子(GBS)方程,即
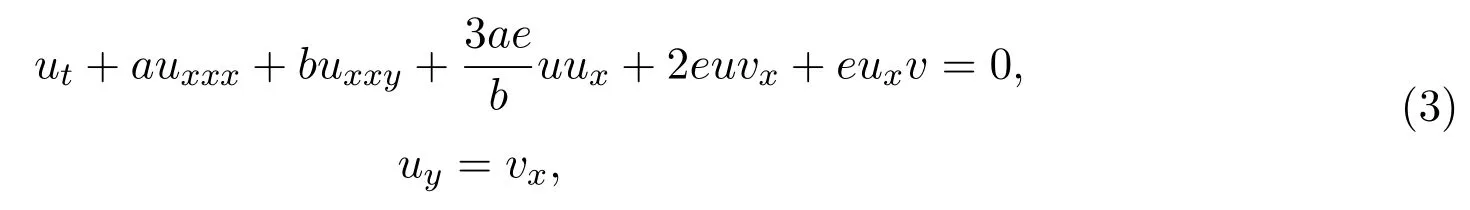
當e=2b時,這個方程就變為(2+1)維KdV方程[15?19]
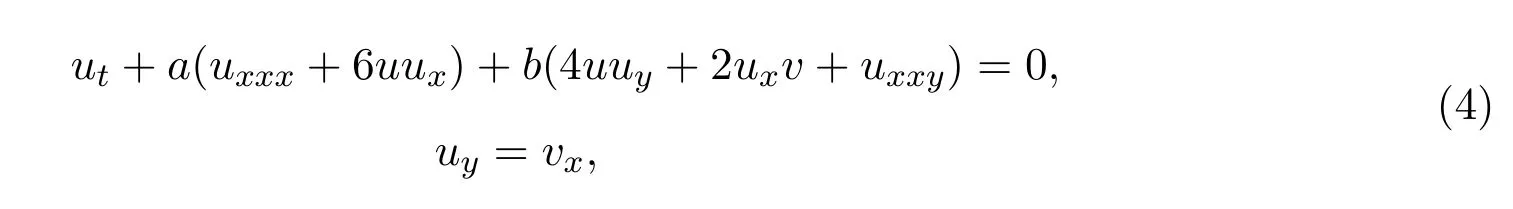
對于特殊的值a=b=1,文獻[15]研究了方程(4)的局域聚合結構.文獻[16]給出了方程(4)的相互作用解.
本文將對方程(3)展開討論.文獻[14]利用Bell多項式研究了這個方程的孤子解與守恒律;文獻[20]給出了它的行波解與周期解;文獻[21]利用多維的Riemann theta函數得到了它的擬周期解,并建立了擬周期解與孤子解之間的聯系.我們將會在文中第二部分,利用截斷的Painlev′e展開法構造方程(3)的非局域對稱.同時利用非局域對稱局域化的方法,通過一個有限變換將其留數對稱轉化為拓展系統的Lie點對稱,進而可由拓展系統的已知解來構造新的解.在文中第三部分,利用Lou[5]提出的CRE方法驗證了(2+1)維GBS方程的CRE可積性,并給出了(2+1)維GBS方程的新的孤波解與橢圓周期波解的相互作用解.
2 非局域對稱及其局域化
根據文獻 [14],我們知道 (2+1)維 GBS系統 (3)是 Painlev′e可積的,它的 Painlev′e截斷展開為
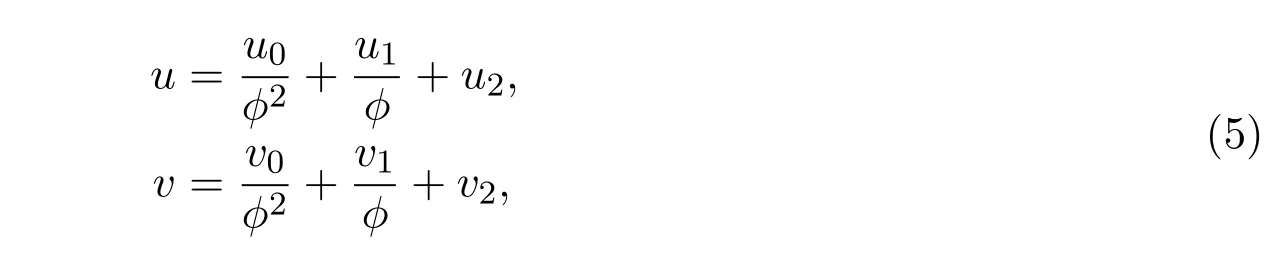
其中u0,u1,u2,v0,v1,v2,?是x,y,t的函數.將(5)代入(3),然后令所得方程中的各次冪系數分別為零,可解得
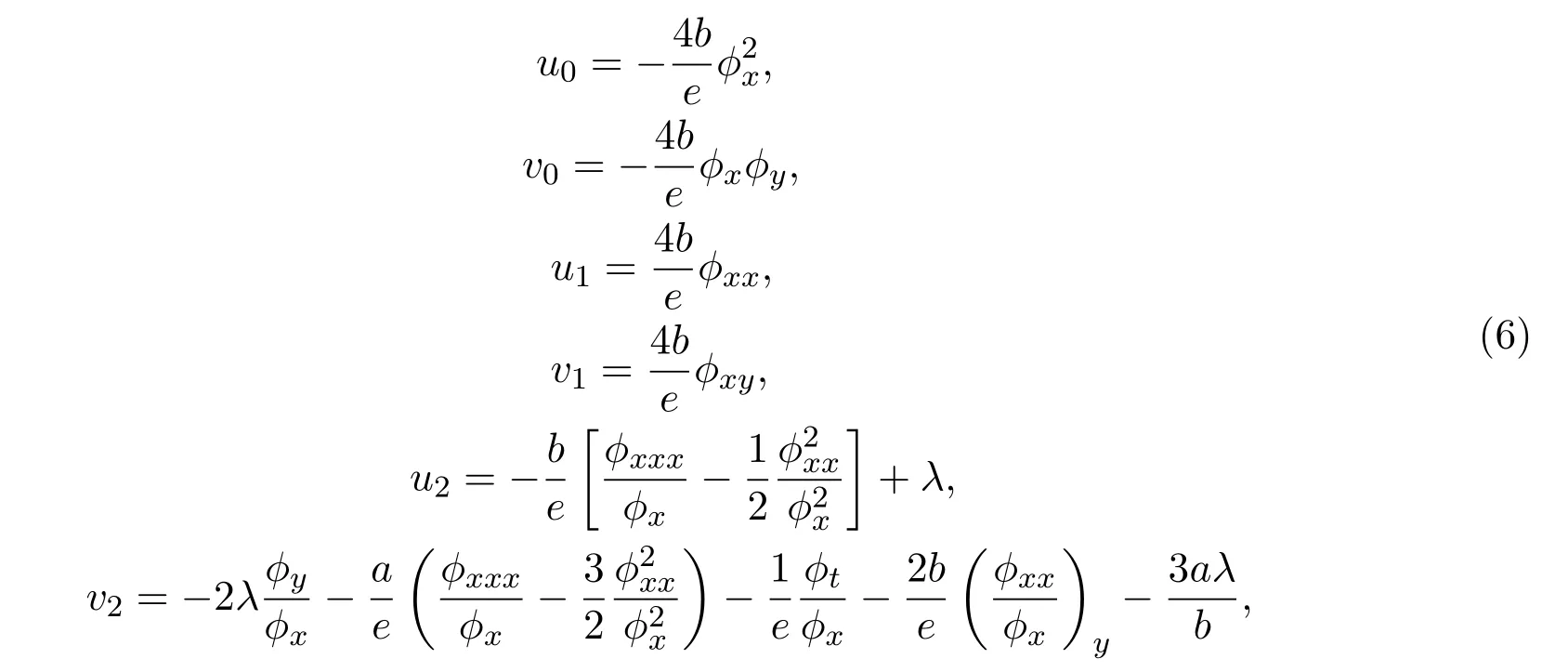
并且u2,v2滿足方程(3),?滿足
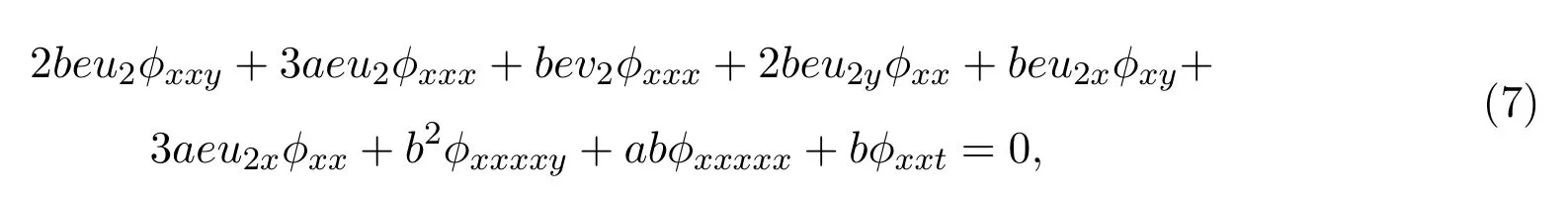
這里λ是任意常數.
令
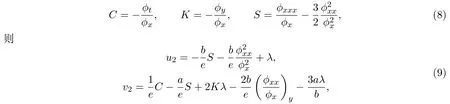
?滿足下面的Schwarzian形式:
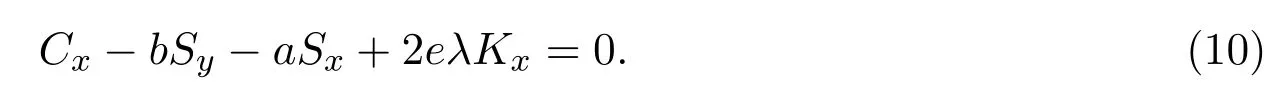
Schwarzian方程(10)在下列M?bious變換下是不變的:
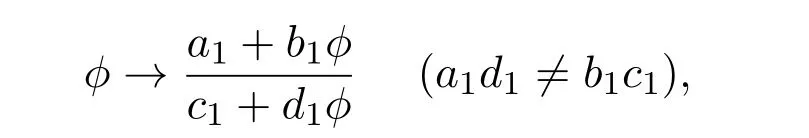
定理 2.1如果場?是方程(10)的解,那么
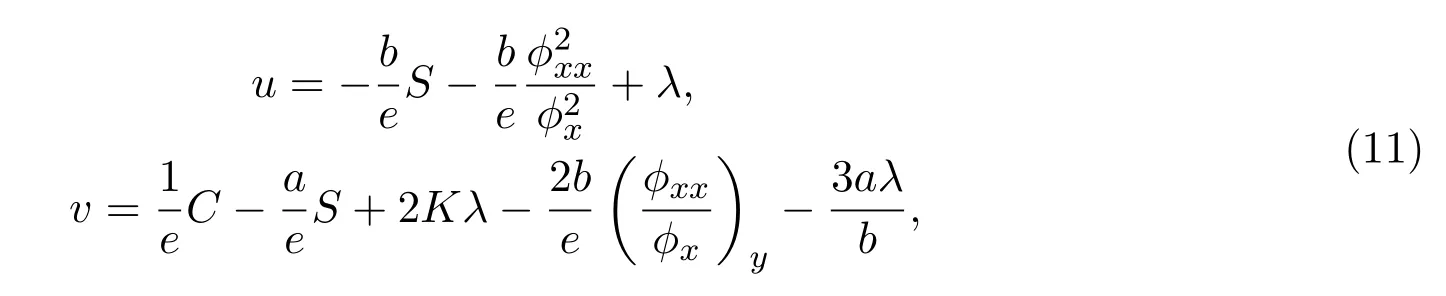
為方程(3)的解,這里C,K,S如(8)定義.
證明將方程(10)和(11)代入(3),即得結論成立.
由留數對稱定理[3],顯然留數u1和v1是方程(3)相應于解u2和v2的對稱,即

為了將非局域對稱u1和v1局域化,我們引入四個新的變量
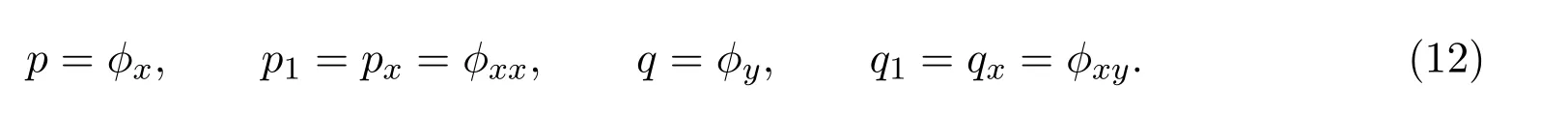
易證(2+1)維GBS方程(3)的非局域對稱可被局域化為以下Lie點對稱:
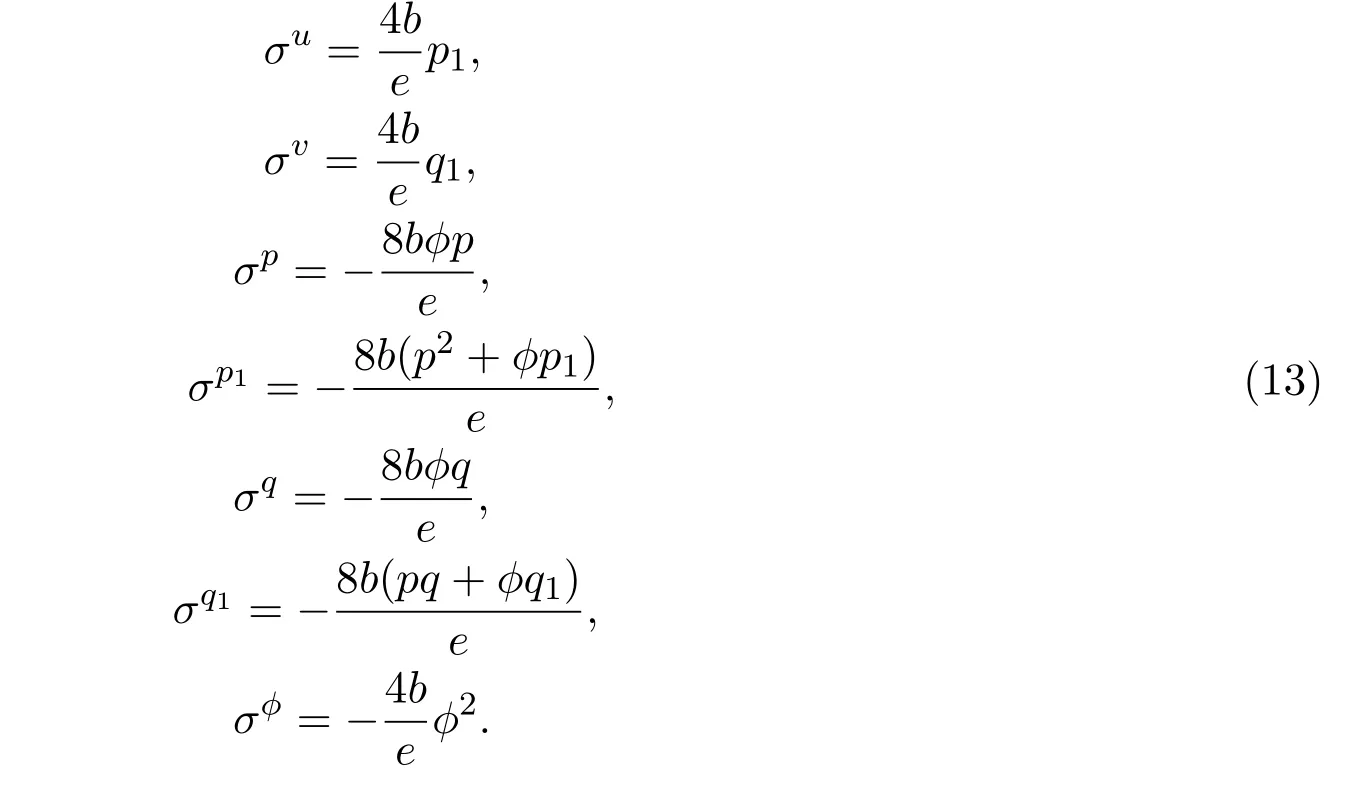
拓展系統(3),(11)和(12)的向量場為:

根據Lie第一基本定理[22],通過解下面的初值問題,我們可以得到Lie點對稱(14)的有限對稱變換群:
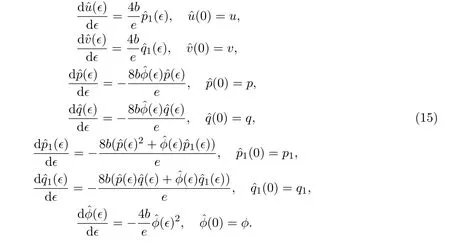
因此,有如下定理:
定理2.2若{u,v,p,q,p1,q1,?}是拓展系統(3),(11)和(12)的解,那么也是該拓展系統的解,其中

3 CRE可解及其相互作用解
3.1 CRE可解
根據文獻[5]中的方法,我們可設方程(3)的解為:
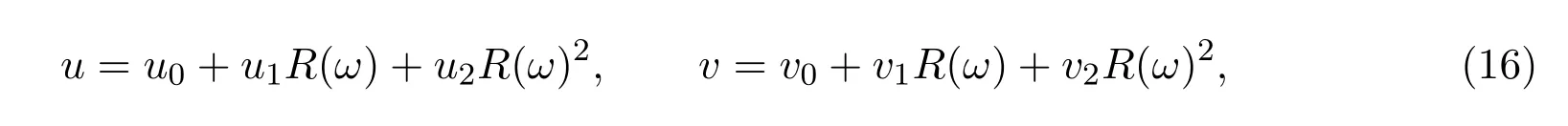
其中 ui,vi,(i=0,1,2),ω是關于x,y和t的函數,且函數R(ω)滿足Riccati方程:
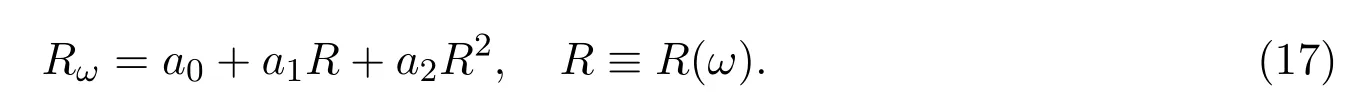
上述方程擁有如下形式的解:
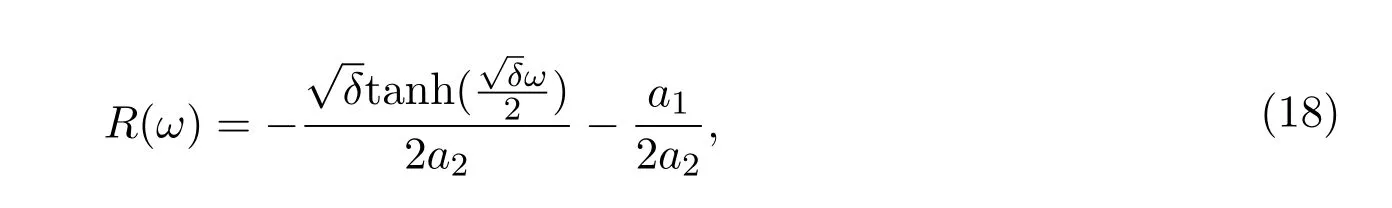
這里
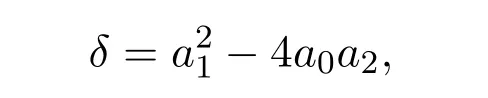
a0,a1,a2為任意常數.
把(16),(17)代入(3),比較 R(ω)的不同次冪的系數,可得

且函數ω需滿足
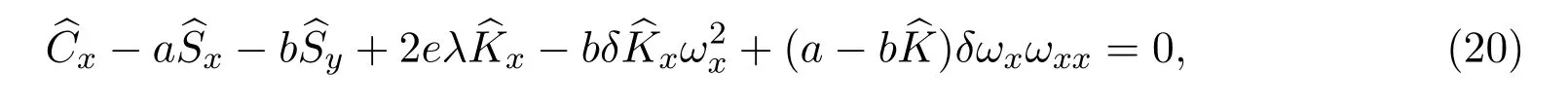
式中
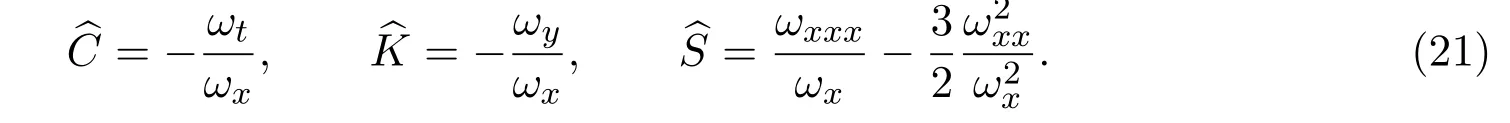
經過計算,R(ω)的各次冪系數均為零,因此,我們可以說(2+1)維GBS方程是CRE可解的.綜上所述,我們有如下定理:
定理 3.1若 ω是方程(20)的解,R(ω)滿足Riccati方程(17),那么
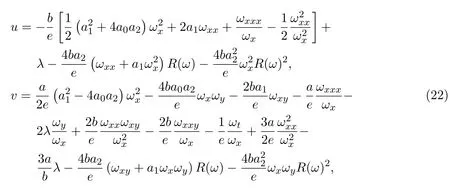
就是(2+1)維GBS方程(3)的解.
3.2 相互作用解
在本文中,我們將構造孤立波與橢圓周期波之間的相互作用解,設方程(20)解的形式為
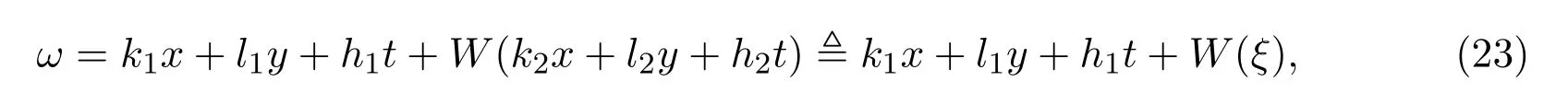
其中
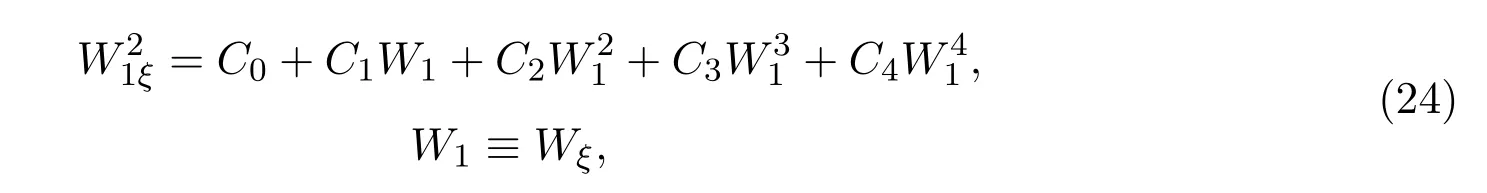
C0,C1,C2,C3,C4為常數.將(23),(24)代入(20),比較W的系數,我們可得到九組解,這里只討論下面三組解:
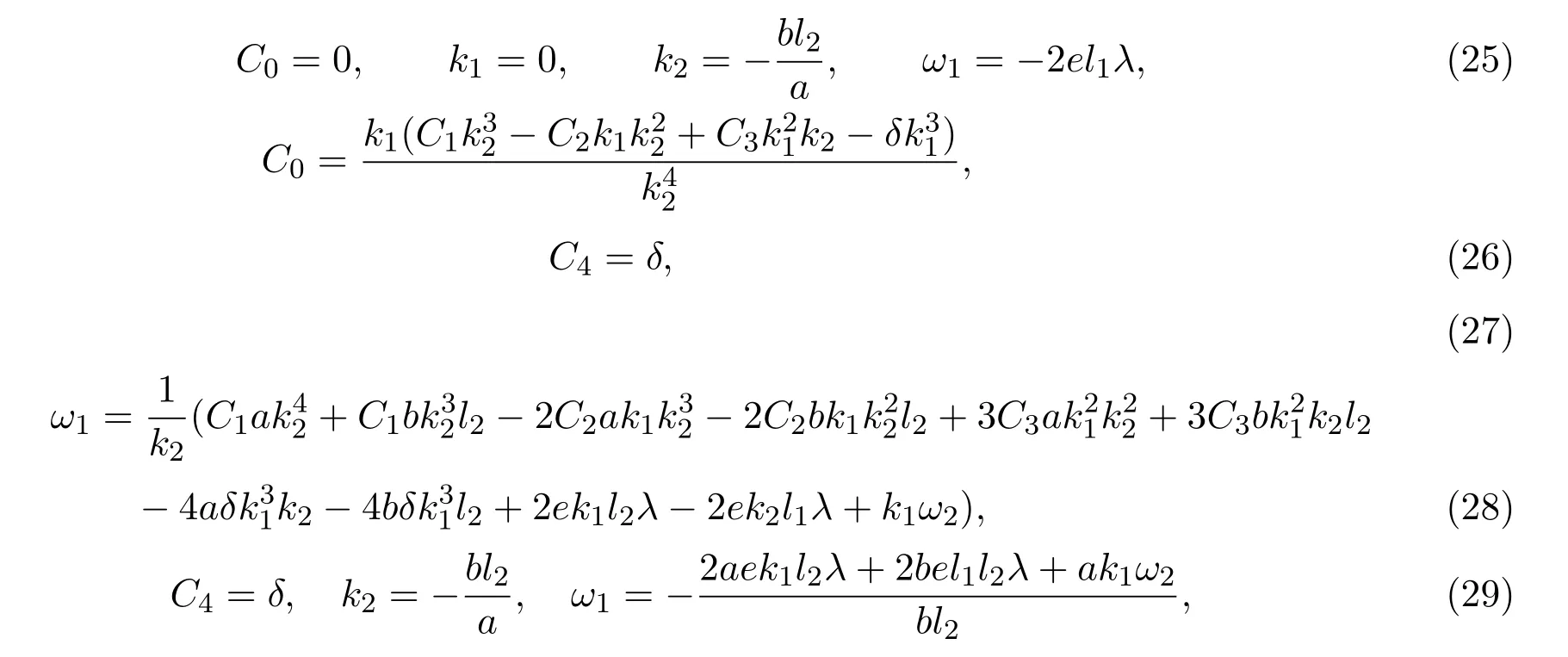
其它的參數均為自由參數.經過分析與計算我們可以知道,(25)與(29)為(28)的特殊情況.
眾所周知,方程(24)的一般解可用Jacobi橢圓函數來表示.為便于更清晰的了解解的形態及性質,我們選擇如下形式的解

其中sn(mξ,n)為一般的橢圓正弦函數.分別將(25),(28),(29)和(30)代入(24),我們將會得到三組解:
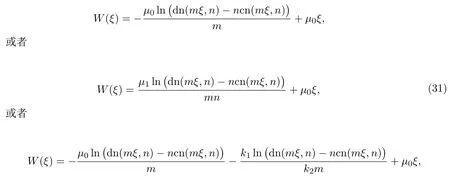
這里cn(mξ,n),dn(mξ,n)均為一般的橢圓函數.在這里我們同樣可以看出,當第三組解中的某些常數取為特殊值后,即可轉化為(31)中的前兩組解.
[1]Weiss J,Tabor M,Carnevale G.The Painlev′e property for partial di ff erential equations[J].Journal of Mathematical Physics,1983,24(3):522-526.
[2]Newell A C,Tabor M,Zeng Y B.A uni fi ed approach to Painlev′e expansions[J].Physica D:Nonlinear Phenomena,1987,29(1-2):1-68.
[3]Lou S Y.Residual symmetries and B?cklund transformations[J].arXiv preprint,arXiv:1308.1140,2013.
[4]Gao X N,Lou S Y,Tang X Y.Bosonization,singularity analysis,nonlocal symmetry reductions and exact solutions of supersymmetric KdV equation[J].Journal of High Energy Physics,2013,2013(5):29.
[5]Lou S Y.Consistent Riccati expansion for integrable systems[J].Studies in Applied Mathematics,2015,134(3):372-402.
[6]Yu W F,Lou S Y,Yu J,et al.Interactions Between Solitons and Cnoidal Periodic Waves of the(2+1)-Dimensional Konopelchenko-Dubrovsky Equation[J].Communications in Theoretical Physics,2014,62(3):297-300.
[7]Ruan S Q,Yu W F,Yu J,et al.The consistent Riccati expansion and new interaction solution for a Boussinesq-type coupled system[J].Chinese Physics B,2015,24(6):060201.
[8]Chen M X,Hu H C,Zhu H D.Consistent Riccati expansion and exact solutions of the Kuramoto-Sivashinsky equation[J].Applied Mathematics Letters,2015,49:147-151.
[9]Wang H,Wang Y H.CRE solvability and soliton-cnoidal wave interaction solutions of the dissipative(2+1)-dimensional AKNS equation[J].Applied Mathematics Letters,2017,69:161-167.
[10]Calogero F,Degasperis A.Nonlinear evolution equations solvable by the inverse spectral transform-I[J].IL Nuovo Cimento B(1971-1996),1976,32(2):201-242.
[11]Cheng W G,Li B,Chen Y.Nonlocal symmetry and exact solutions of the(2+1)-dimensional breaking soliton equation[J].Communications in Nonlinear Science and Numerical Simulation,2015,29(1):198-207.
[12]Cheng W G,Li B,Chen Y.Construction of soliton-cnoidal wave interaction solution for the(2+1)-dimensional breaking soliton equation[J].Communications in Theoretical Physics,2015,63(5):549-553.
[13]Yildiz G,Daghan D.Solution of the(2+1)dimensional breaking soliton equation by using two di ff erent methods[J].Journal of Engineering Technology and Applied Sciences,2016,1(1):11-16.
[14]Xu G Q.Integrability of a(2+1)-dimensional generalized breaking soliton equation[J].Applied Mathematics Letters,2015,50:16-22.
[15]Peng Y Z.A new(2+1)-dimensional KdV equation and its localized structures[J].Communications in Theoretical Physics,2010,54(5):863-865.
[16]Chen J C,Ma Z Y.Consistent Riccati expansion solvability and soliton-cnoidal wave interaction solution of a(2+1)-dimensional Korteweg-de Vries equation[J].Applied Mathematics Letters,2017,64:87-93.
[17]Wang Y H,Chen Y.Binary Bell polynomial manipulations on the integrability of a generalized(2+1)-dimensional Korteweg-de Vries equation[J].Journal of Mathematical Analysis and Applications,2013,400(2):624-634.
[18]Lü X,Lin F H,Qi F H.Analytical study on a two-dimensional Korteweg-de Vries model with bilinear representation,B?cklund transformation and soliton solutions[J].Applied Mathematical Modelling,2015,39(12):3221-3226.
[19]Chai J,Tian B,Sun W R,et al.Solitons and dynamic analysis for a(2+1)-dimensional breaking soliton equation[J].Superlattices and Microstructures,2017,101:584-591.
[20]Wazwaz A M.A New Integrable(2+1)-dimensional generalized breaking soliton equation:N-soliton solutions and traveliwave Solutions[J].communications in theoretical physics,2016,66(4):385-388.
[21]Zhao Z L,Han B.Quasiperiodic wave solutions of a(2+1)-dimensional generalized breaking soliton equation via bilinear B?cklund transformation[J].The European Physical Journal Plus,2016,131(5):128.
[22]Bluman G W,Kumei S.Symmetries and Di ff erential Equations[M].New York:Springer,1989.
Nonlocal symmetries and interaction solutions for the new(2+1)dimensional generalized breaking soliton equation
Bai Xirui,Wo Weifeng
(Department of Mathematics,Ningbo University,Ningbo 315211,China)
According to the truncated Painlev′e expansion and consistent Riccati expansion(CRE)method,the nonlocal symmetry for the 2+1-dimensional generalized breaking soliton equation is derived.Moreover,the symmetry group related to Schwarzian can be obtained by the method of localization.Meanwhile,this equation has been proved to be CRE solvable,and the interaction solutions between solitons and cnoidal waves are given.
(2+1)-generalized breaking soliton equation,nonlocal symmetry,CRE method,interaction solutions
O175.2
A
1008-5513(2017)05-0536-09
10.3969/j.issn.1008-5513.2017.05.012
2017-09-24.
國家自然科學基金(11201249);浙江省自然科學基金(LY16A010002).
白喜瑞(1987-),碩士,研究方向:偏微分方程.
沃維豐(1981-),博士,講師,研究方向:偏微分方程.
2010 MSC:22E70,35Q68,68W30,35C08

