淺談初中幾何添加輔助線的幾點策略

陳莉娜

一、問題背景

初中平面幾何是一門提高學生邏輯思維和分析能力的學科。對于大部分學生來說學習起來比較困難，往往學生最為頭痛的就是如何在這些錯綜復雜的幾何圖形去添加合適的輔助線，其實添加輔助線也是有規律可循，教師在教學的過程中，不但要引導學生對知識進行系統的整理，同時也要引導學生對教材深入挖掘、提煉總結其思想實質，揭示歸納方法因素，以其更好地發揮思想方法的整體功效，從而提高解題技巧。

二、問題研究

（一） 中點模型的構造

1、考情分析

三角形是初中幾何的重要內容之一，也是歷年中考命題的熱點，其中，三角形各邊的中點、中線及中位線的有關性質的應用，是中考的必考內容，歷年來多以計算和證明題的形式出現。通過對近幾年中考有關試題的分析，預計與中點有關的操作性試題和綜合性的探究題將是今后幾年中考數學的重點題型。

2、技巧提煉

很多幾何題會給出“點X是線段XX的中點”這樣的條件，那么看到“中點”應該想到什么呢？“中點”有哪些作用呢？

已知任意三角形一邊上的中點，可以考慮：

（1） 倍長中線或類中線（與中點有關的線段）構造全等三角形。如圖（a）、圖（b）所示。

（2） 三角形中位線定理。

（3） 已知直角三角形斜邊中點，可以考慮構造斜邊中線。

（4） 已知等腰三角形底邊中點，可以考慮與頂點連接用“三線合一”。

有些題目的中點不直接給出，此時需要我們挖掘題目中的隱含中點，例如直角三角形中斜邊中點，等腰三角形底邊上的中點，當沒有這些條件的時候，可以用輔助線添加。

3、 例題精講

如圖所示，已知在△ABC中，AD是BC邊上的中線，E是AD上一點，聯結BE并延長交AC于點F，AF=EF，求證：AC=BE。

【思路點撥】遇到中線，我們考慮倍長中線或類中線，因為AD是中線，所以加倍延長AD至點G，使DG=DA，聯結BG，構造全等三角形，進行導角；或者加倍延長ED，構造全等三角形，再進行導角。

證法一：如圖（a）所示，延長AD至點G，使DG=AD，聯結BG.

∵DB=DC，∠BDG=∠CDA，AD=GD.

∴△ADC≌△GDB，∴AC=GB，∠G=∠EAF.

又∵AF=EF，∴∠EAF=∠AEF.

∵∠AEF=∠BED，

∴∠G=∠BED，∴BE=BG，∴BE=AC.

證法二：如圖（b）所示，延長ED至點G，使得DG=DE，聯結CG.

∵點D是BC的中點，∴BD=CD.

∴∠BDE=∠CDG，∴△BED≌CGD.

∴∠G=∠BED，BE=CG.

∵AF=EF，∴∠FAE=∠AEF=∠BEG.

∴∠G=∠DAC，即∠G=∠EAF，

∴AC=GC.

∴AC=BE。

變式訓練

如圖所示，在△ABC中，AD交BC于點D，點E是BC中點，EF∥AD交CA的延長線于點F，交AB于點G，若AD為△ABC的角平分線，求證：BG=CF.

【思路點撥】因為E是中點，所以加倍延長FE至點H，使EH=EF，聯結BH構造全等三角形，進行導角。

證法一：如圖（a）所示，延長FE到點H，使HE=FE，聯結接BH。

∵CE=BE，∠CEF=∠BEH，FE=HE，

∴△CEF≌△BEH（SAS）.∴∠F=∠H，CF=BH.

∵AD平分∠BACA，∴∠1=∠2.

∵AD∥EF，∴∠1=∠AGF=∠2=∠F=∠BGH.

∴∠BHG=∠BGH，∴BG=BH.∴BG=CF.

證法二：如圖（b）所示，取AB的中點Q，聯結EQ，則EQ=?AC，EQ∥AC，∴∠QEG=∠F.

∵EF∥AD，∴∠F=∠2=∠1.

∵∠QGE=∠1，∠QEG=∠F，∠FGA=∠1，

∴∠F∠FGA，∠QGE=∠QEG，

故EQ=GQ，AF=AG.

∵BQ=AQ=GQ+AG，

∴BG=BQ+GQ=2GQ+AG.

∵2GQ=2EQ=AC，∴BG=AC+AF=CF.

（二） 角平分線模型的構造

1、考情分析

三角形內外角平分線的概念是處理與角相關問題的基本依據和方法，在中考題中經常利用角平分線的性質去證明線段相等、角相等或三角形全等。隨著課改的深入，中考的題型也發生了變化。利用角平分線的對稱性把圖形翻折，再進行推理計算，以及與角平分線有關的探究題、綜合題成為近幾年中考的熱點題型。

2、技巧提煉

與角平分線有關的常用輔助線作法，即角平分線的四大基本模型。

已知P是∠MON平分線上一點，

（1）若PA⊥OM于點A，如下圖（a）所示，可以過P點作PB⊥ON于點B，則PB=PA.可記為“圖中有角平分線，可向兩邊作垂線”。

（2）若點A是射線OM上任意一點，如下圖（b）所示，可以在ON上截取OB=OA，連接PB，構造△OPB≌△OPA.可記為“圖中有角平分線，可以將圖對折看，對稱以后關系現”。

（3）若AP⊥OP于點P，如上圖（c）所示，可以延長AP交ON于點B，構造△AOB是等腰三角形，P是底邊AB的中點。可記為“角平分線加垂線，三線合一試試看”。

（4）若過點P作PQ∥ON交OM于點Q，如上圖（d）所示，可以構造△POQ是等腰三角形，可記為“角平分線 + 平行線，等腰三角形必呈現”。endprint

3、例題講解

已知：如圖所示，△ABC的外角∠ACD的平分線CP與內角∠ABC的平分線BP交于點P，連接AP、CP，若∠BPC=40°，求∠CAP的度數。

由題意可證∠BAC=2∠BPC.又∠BPC=40°，

∴∠BAC=80°，如下圖所示，過P分別作

PE⊥CD，PF⊥AC，PG⊥BA，垂足分別為E、F、G.由角平分線的性質，得PE=PF，PE=PG，∴PF=PG.

∴∠CAP=?∠CAG=?（180°-80°）=?×100°=50°。

（三） 弦圖模型的構造

1、考情分析

勾股定理的證明，從古至今引起無數人的關注，其證法到現在已有五百多種，“弦圖”就是我國三國時期的數學家趙爽，利用面積相等，形象巧妙的證明方法。隨著課改的深入，利用弦圖或其衍生圖來解決數學問題，已成為中考的熱點題型。預計與弦圖相關的中考題型有填空題、選擇題、計算題及探究題，對探究題要多加注意；同時在解題時；要掌握作輔助線構造弦圖的方法。

2、 技巧提煉

勾股定理的證明方法是多樣的，而其中的多種方法是具有共性的。觀察發現：很多圖形中都可以提煉出一個相同的圖形——三垂直全等模型。如右圖所示。

三垂直全等模型其實是從弦圖中衍生出來的一個模型，當我們解直角三角形或者正方形的試題時，在很多情況下我們可以考慮構造弦圖來解決，有時候是完整的弦圖，有時只需一半弦圖——三垂直全等模型。

右圖是三垂直全等模型經過直角三角形位置的變化之后所得到的另外兩個有三垂直和全等三角形的圖形，僅供做題時參考。

3、例題講解

如圖所示，向△ABC的外側做正方形ABDE，正方形ACFG.過點A作AH⊥BC于點H，AH的反向延長線與EG交于點P，

求證：（1）EP=GP；（2）BC=2AP.

證明：（1）如下圖所示，過點E，G分別作AP的垂線，垂足為M，N.

∴∠M=∠GNM=90°

.∵AH⊥BC，∴∠AHB=90°∴∠AHB=∠M.

∵四邊形ABDE是正方形，

∴AB=AE，∠EAB=90°.∴∠1+∠2=90°.

∵∠2+∠ABH=90°，∴∠ABH=∠1.

∴△ABH≌△AEM.∴AH=EM，BH=AM.

同理可證△ACH≌△AGN

∴AH=GN，CH=AN.∴EM=GN.

∠EPM=∠GPN，∠M=∠GNM，

∴△EPM≌△GPN.

∴EP=PG.

（2）由（1）得，PM=PN.∵BC=BH+CH，

∴BC=AM+AN=AP+PM+AP-PN=2AP.

（四） 梯形中的輔助線問題

1、考情分析

“梯形”是近幾年來中考數學綜合題中的中點和熱點題型，利用梯形的性質和它多種輔助線的添加，來證明線段相等，及進行線段、角、梯形周長和面積的計算，是中考的常見題型。

2、 技巧提煉

初二幾何中梯形面積公式的教學，教材中給出作對角線、把梯形分成兩個三角形的解法，教學中不應該停留在這種表層的認識上，應引導學生這種方法的深層次含義，既通過“分解與組合”思想，實現把未知問題轉化為已知問題，并進而引導學生運用這種思想方法去探求問題的其他解法，培養學生思維的靈活性。在梯形中常見的有以下六種題型：

（1） 已知兩底之差或求兩底之差的題型，常過上底的一個端點添一腰的平行線與下底相交；達到把梯形分解成一個平行四邊形與三角形的目的；求（圖1）；

（2） 已知梯形的上底和底，求面積，常過上底的兩個端點向下底作垂線，添高；（圖2）；

（3） 延長兩腰交于一點，可得到一對相似三角形 （圖3）；

（4） 已知梯形對角線相等或互相垂直的題型，常過上底的一個端點作一對角線的平行線，與下底的延長線相交，體現組合的思想（圖4）；

（5） 有中點時，常過一腰的中點作另一腰的平行線，分別與上底的延長線、下底相交（圖5）；

（6） 有中點時，也常連接上底的一端點與另一腰的中點并延長，與下底的延長線相交（圖6）。

3、 例題

已知等腰梯形ABCD的高是9㎝，AB∥CD，A C⊥BD，求它的面積。

（五）圓中的輔助線問題

1、考情分析

“圓”是近幾年中考的重點內容，圓的概念和性質的考查主要以填空和選擇題的形式出現，與圓的切線有關的證明題和計算題則出在解答題中。縱觀近幾年的中考題，圓心角的有關運算，垂徑定理的應用，弧長、扇形、的計算在今后也還是中考的常見題型，而圓的切線的證明和計算，以及圓與銳角三角比、四邊形、函數、方程等結合的綜合題、探究題、開放題、動態題，將是中考的重點題型。

2、技巧提煉

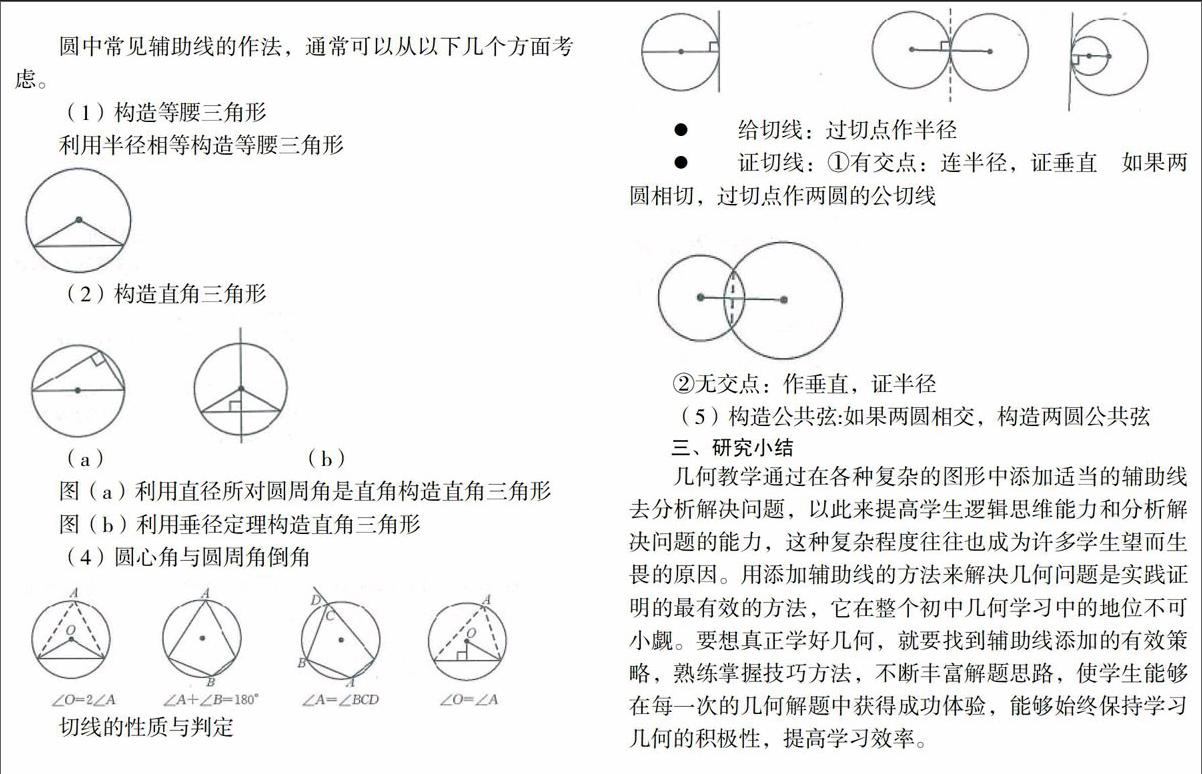
圓中常見輔助線的作法，通常可以從以下幾個方面考慮。

（1）構造等腰三角形

利用半徑相等構造等腰三角形

（2）構造直角三角形

（a） （b）

圖（a）利用直徑所對圓周角是直角構造直角三角形

圖（b）利用垂徑定理構造直角三角形

（3） 圓心角與圓周角倒角

（4）切線的性質與判定

給切線：過切點作半徑

證切線：①有交點：連半徑，證垂直 如果兩圓相切，過切點作兩圓的公切線

②無交點：作垂直，證半徑

（5）構造公共弦：如果兩圓相交，構造兩圓公共弦

三、研究小結

幾何教學通過在各種復雜的圖形中添加適當的輔助線去分析解決問題，以此來提高學生邏輯思維能力和分析解決問題的能力，這種復雜程度往往也成為許多學生望而生畏的原因。用添加輔助線的方法來解決幾何問題是實踐證明的最有效的方法，它在整個初中幾何學習中的地位不可小覷。要想真正學好幾何，就要找到輔助線添加的有效策略，熟練掌握技巧方法，不斷豐富解題思路，使學生能夠在每一次的幾何解題中獲得成功體驗，能夠始終保持學習幾何的積極性，提高學習效率。endprint