自我質(zhì)疑機(jī)制下公共物品博弈模型的相變特性?

楊波 范敏 劉文奇 陳曉松

1)(昆明理工大學(xué)數(shù)據(jù)科學(xué)研究中心,昆明 650500)

2)(昆明理工大學(xué)理學(xué)院,昆明 650500)

3)(中國(guó)科學(xué)院理論物理研究所,理論物理前沿重點(diǎn)實(shí)驗(yàn)室,北京 100190)

4)(中國(guó)科學(xué)院大學(xué)物理科學(xué)學(xué)院,北京 100049)

自我質(zhì)疑機(jī)制下公共物品博弈模型的相變特性?

楊波1)2)?范敏1)2)劉文奇1)2)陳曉松3)4)

1)(昆明理工大學(xué)數(shù)據(jù)科學(xué)研究中心,昆明 650500)

2)(昆明理工大學(xué)理學(xué)院,昆明 650500)

3)(中國(guó)科學(xué)院理論物理研究所,理論物理前沿重點(diǎn)實(shí)驗(yàn)室,北京 100190)

4)(中國(guó)科學(xué)院大學(xué)物理科學(xué)學(xué)院,北京 100049)

公共物品博弈是研究群體相互作用的經(jīng)典模型,廣泛用于解釋自私個(gè)體間合作的涌現(xiàn)和保持.本文從理論分析和蒙特卡羅模擬兩個(gè)方面研究了二維正方格子上一個(gè)有償懲罰機(jī)制下隨自我質(zhì)疑更新規(guī)則演化的公共物品博弈模型的相變特性.理論分析方面,將公共物品博弈模型轉(zhuǎn)化為一個(gè)外場(chǎng)不為零的鐵磁Ising模型.通過(guò)有效能量發(fā)現(xiàn):不存在懲罰時(shí),個(gè)體間的耦合強(qiáng)度為零,體系只有外場(chǎng)作用;存在懲罰時(shí),個(gè)體間包含最近鄰、次近鄰和第三近鄰相互作用且外場(chǎng)不為零.蒙特卡羅模擬方面,首先驗(yàn)證了理論分析的正確性,然后對(duì)公共物品博弈模型相關(guān)的一級(jí)相變和二級(jí)相變進(jìn)行了有限尺度標(biāo)度分析.研究發(fā)現(xiàn):1)蒙特卡羅模擬所得結(jié)果與類(lèi)Ising模型分析結(jié)果完全吻合;2)相比二維Ising模型,公共物品博弈的二級(jí)相變臨界指數(shù)發(fā)生了變化;3)公共物品博弈的一級(jí)相變與二維Ising模型相同.

Ising模型,有限尺度標(biāo)度理論,蒙特卡羅模擬,自我質(zhì)疑更新規(guī)則

1 引 言

演化博弈理論(evolutionary game theory)突破了傳統(tǒng)博弈論關(guān)于“理性人”和“完全信息”的限制,它強(qiáng)調(diào)有限理性的博弈個(gè)體在重復(fù)博弈過(guò)程中根據(jù)自身掌握的局部信息,通過(guò)自適應(yīng)學(xué)習(xí)做出盡可能占優(yōu)的策略［1,2］.在人類(lèi)社會(huì)和自然界中,自私個(gè)體之間產(chǎn)生合作是一個(gè)“驚人”的現(xiàn)象,得到了許多學(xué)者的重視和研究［3,4］.空間演化博弈理論(將多個(gè)個(gè)體放置在社會(huì)網(wǎng)絡(luò)上進(jìn)行重復(fù)博弈)的提出從空間結(jié)構(gòu)和社會(huì)網(wǎng)絡(luò)的角度很好地解釋了合作的涌現(xiàn),同時(shí)也開(kāi)啟了演化博弈研究的新篇章［1,2,5,6］.

公共物品博弈(public goods game)是一種典型的多人空間演化博弈模型,在博弈過(guò)程中,N個(gè)參與者獨(dú)立決定向公共池子投資(合作)或不投資(不合作),初始投資總額通過(guò)增益系數(shù)放大r(1＜r＜N)倍后,平均分給群組內(nèi)所有個(gè)體,無(wú)論初始投資與否.顯然,采用不合作策略可以在事先不進(jìn)行任何投資的情況下獲得收益,搭上合作者的便車(chē).公共物品博弈生動(dòng)再現(xiàn)了個(gè)人與集體間的矛盾,有著廣泛的應(yīng)用,如:在班級(jí)大掃除中,每個(gè)學(xué)生付出的勞動(dòng)是不對(duì)等的,但干凈明亮的學(xué)習(xí)環(huán)境卻是大家一起共享的.盡管所有成員都合作時(shí),群組可以實(shí)現(xiàn)利益最大化,然而對(duì)一個(gè)自私且理性的個(gè)體而言,最優(yōu)策略是選擇背叛.從而在個(gè)體最優(yōu)策略與群組最優(yōu)策略之間形成了社會(huì)困境,即所謂的公共品悲劇(the tragedy of the commons)［1,7?9］.然而,現(xiàn)實(shí)生活中這種悲劇并未出現(xiàn).為了解釋合作的廣泛傳播與個(gè)體的自私性之間的矛盾,許多機(jī)制被相繼提出,如:期望誘導(dǎo)重連機(jī)制、刪邊機(jī)制、懲罰機(jī)制、獎(jiǎng)勵(lì)機(jī)制、社會(huì)多樣性機(jī)制、馬太效應(yīng)、志愿者參與機(jī)制、遷徙機(jī)制、調(diào)整投資機(jī)制、自適應(yīng)有限投資反饋機(jī)制和條件策略［10,11］等.本文基于前人對(duì)懲罰機(jī)制的研究［12?18］,采用一類(lèi)簡(jiǎn)化的有償懲罰機(jī)制作用下的公共物品博弈模型進(jìn)行研究.

空間演化博弈的兩個(gè)研究重點(diǎn)是策略更新規(guī)則和網(wǎng)絡(luò)的空間結(jié)構(gòu)［1］.網(wǎng)絡(luò)演化博弈的策略更新規(guī)則可以劃分為兩類(lèi):學(xué)習(xí)機(jī)制（模仿）和自我質(zhì)疑機(jī)制（自省）.學(xué)習(xí)機(jī)制主要是向網(wǎng)絡(luò)中的最近鄰學(xué)習(xí),包括學(xué)習(xí)鄰居中收益最大的［5］;以一定的概率學(xué)習(xí)那些收益比自己高的個(gè)體們［19,20］;任意選擇最近鄰中的一個(gè),比較收益差,以較大的概率模仿收益比自己高的個(gè)體［21?23］.自我質(zhì)疑機(jī)制的研究相對(duì)較少［24?27］,它是指任意博弈個(gè)體先計(jì)算當(dāng)前策略所得總收益,然后采用自身反策略進(jìn)行一次虛擬博弈,并計(jì)算虛擬總收益,通過(guò)比較當(dāng)前博弈和虛擬博弈收益變化的多少,來(lái)決定自己下一局所采用的策略.自我質(zhì)疑機(jī)制與統(tǒng)計(jì)物理中Ising模型的單自旋翻轉(zhuǎn)蒙特卡羅模擬方法十分類(lèi)似.基于此,本文研究自我質(zhì)疑更新規(guī)則下的公共物品博弈模型與Ising模型的等價(jià)關(guān)系［28］.之前,演化博弈模型的相關(guān)研究主要依靠計(jì)算機(jī)模擬方法,本文提出的類(lèi)Ising方法將為該領(lǐng)域的研究提供理論基礎(chǔ).值得一提的是,經(jīng)濟(jì)學(xué)中廣泛研究的隨機(jī)最優(yōu)反應(yīng)均衡(quantal response equilibrium,QRE)與自我質(zhì)疑機(jī)制十分類(lèi)似,它用隨機(jī)反應(yīng)代替?zhèn)鹘y(tǒng)的最優(yōu)反應(yīng),將納什均衡作為它的一個(gè)特例進(jìn)行處理［29?31］.

本文提出一個(gè)有償懲罰機(jī)制下按自我質(zhì)疑機(jī)制演化的公共物品博弈模型,從以下三個(gè)方面展開(kāi)研究.理論分析方面,找到與該演化博弈模型等價(jià)的Ising模型并運(yùn)用相關(guān)理論進(jìn)行分析預(yù)測(cè);蒙特卡羅模擬方面,驗(yàn)證理論分析的結(jié)果;相變特性方面,任選一組懲罰參數(shù),研究博弈模型中伴隨的相變現(xiàn)象,分析相變的種類(lèi),測(cè)定相關(guān)臨界指數(shù).

2 自我質(zhì)疑更新規(guī)則下的公共物品博弈模型

2.1 模型的引入

在由N個(gè)個(gè)體參與的公共物品博弈中,每個(gè)個(gè)體都有兩種策略可供選擇,投資或不投資,假設(shè)原始投資額為1.投資總額放大r倍后(可認(rèn)為是投資后獲利),平均分給群組內(nèi)所有參與博弈的個(gè)體,而不管個(gè)體是否向公共池內(nèi)投過(guò)資,其中r為強(qiáng)化因子(enhancement factor),滿足1＜r＜N.假設(shè)群組內(nèi)有N+個(gè)合作者,則投資者的收益為gC=rN+/N?1,而不投資者的收益為gD=rN+/N.顯然,不投資者的收益永遠(yuǎn)大于投資者的收益.所以,不投資者可以在投資者投資的基礎(chǔ)上“搭便車(chē)”.從而,公共物品博弈的納什均衡是,所有人都不投資.為了解釋自私個(gè)體間仍有合作行為產(chǎn)生,本文提出一種簡(jiǎn)化的有償懲罰機(jī)制,即懲罰的代價(jià)為C(cost),被懲罰者的處罰額度為F( fi ne).此時(shí),投資者的收益為gC=rN+/N?1?C(N?N+),不投資者獲得收益gD=rN+/N?FN+.

采用一個(gè)固定的網(wǎng)絡(luò)來(lái)刻畫(huà)個(gè)體之間的博弈關(guān)系.在網(wǎng)絡(luò)模型確定之后,種群中的個(gè)體占據(jù)網(wǎng)絡(luò)中的節(jié)點(diǎn).每個(gè)個(gè)體都是純策略者并只能選擇合作或者不合作策略.每個(gè)個(gè)體與自己的鄰居組成一個(gè)群體進(jìn)行公共品博弈.在每一輪博弈中,任選一個(gè)個(gè)體i,然后根據(jù)自我質(zhì)疑機(jī)制決定是否改變當(dāng)前策略.即選定個(gè)體i后,個(gè)體i采用當(dāng)前策略與周?chē)従硬┺墨@得當(dāng)前收益Gi,采用當(dāng)前策略的反策略與周?chē)従舆M(jìn)行一次虛擬博弈,獲得虛擬收益?zhèn)€體i通過(guò)比較當(dāng)前收益和虛擬收益,以一定概率決定是否改變當(dāng)前策略,概率的選擇為

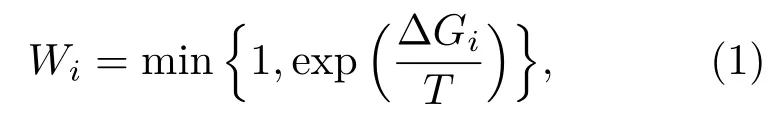
2.2 公共物品博弈模型與Ising模型間的轉(zhuǎn)化關(guān)系

在空間網(wǎng)絡(luò)中,任意個(gè)體i,不僅與周?chē)罱弬€(gè)體博弈,還與次近鄰進(jìn)行博弈.即個(gè)體i不僅參與以自己為中心節(jié)點(diǎn)進(jìn)行的群體博弈,而且參與以鄰居為中心節(jié)點(diǎn)的群體博弈,即總共經(jīng)歷ki+1次博弈,其中ki為節(jié)點(diǎn)i的度.當(dāng)個(gè)體i參與以自己為中心節(jié)點(diǎn)的群體博弈時(shí),參與博弈的個(gè)體總數(shù)為ki+1,當(dāng)參與鄰居j為中心節(jié)點(diǎn)的群體博弈時(shí),參與人數(shù)為kj+1.圖1顯示了二維格點(diǎn)上個(gè)體i參與的五次公共物品博弈,深色格子表示博弈過(guò)程中的中心節(jié)點(diǎn),淺色格子表示中心節(jié)點(diǎn)的最近鄰節(jié)點(diǎn),每輪博弈在由深色和淺色節(jié)點(diǎn)組成的群體中進(jìn)行,白色格子表示其余節(jié)點(diǎn).

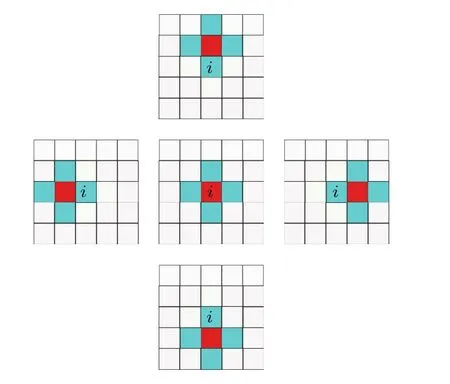
圖1 (網(wǎng)刊彩色)二維正方格子上任意個(gè)體i每輪博弈中參與以不同節(jié)點(diǎn)為中心的五次公共物品博弈Fig.1.(color online)The public goods games which involve player i on two-dimension square lattice each round.

個(gè)體i每一輪博弈的收益來(lái)自于ki+1個(gè)群體博弈所得收益的總和,為便于推導(dǎo),用Si表示個(gè)體i的策略,有兩種取值,Si=+1表示合作,Si=?1表示不合作,在以i為中心結(jié)點(diǎn)的群體博弈中,當(dāng)Si=+1時(shí),

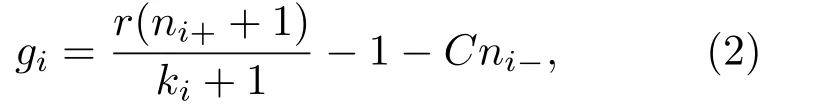
其中ni+表∑示i的鄰居中采用合作策略的個(gè)體總和,ni+=j(1+Sj/2);ni?表示∑i的鄰居中采用不合作∑策略的個(gè)體總和,ni?=j(1?Sj)/2=(ki?jSj)/2,j是i的最近鄰.當(dāng)Si=?1時(shí),

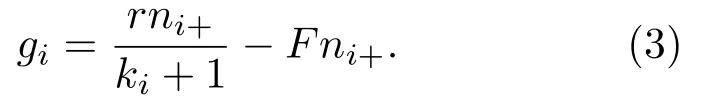
個(gè)體i翻轉(zhuǎn)所帶來(lái)的收益差為

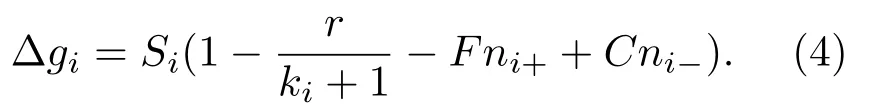
將ni+和ni?的表達(dá)式代入(4)式,并用新記號(hào)?gii描述個(gè)體i在以i為中心節(jié)點(diǎn)進(jìn)行博弈的過(guò)程中所帶來(lái)的收益變化,

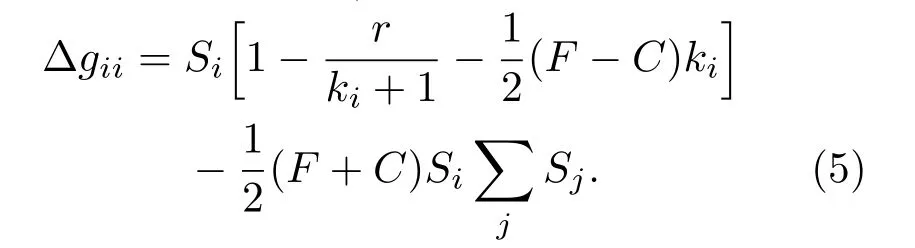
同理可得,?gij,個(gè)體i在以j為中心節(jié)點(diǎn)進(jìn)行博弈時(shí),改變策略帶來(lái)的收益差為

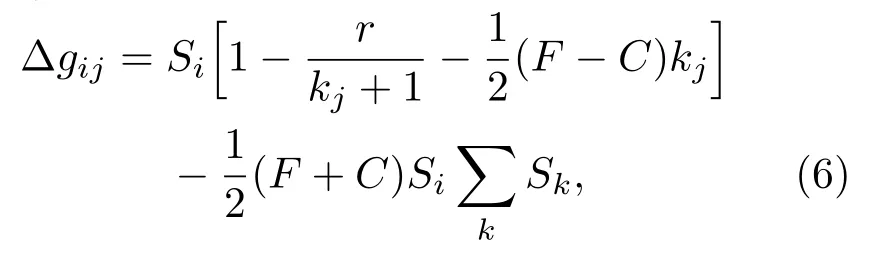
其中,j是i的最近鄰,表示對(duì)i的最近鄰求和;表示在以j為中心的博弈群體中,對(duì)除i以外的節(jié)點(diǎn)進(jìn)行求和.從而,一輪博弈中i改變策略帶來(lái)的總收益差?Gi為

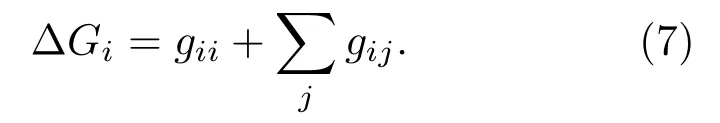
將(5)式和(6)式代入(7)式,并整理可得

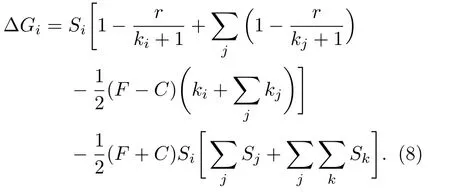
從上面的表達(dá)式可以看出,總收益的改變由兩部分組成:前面部分只與博弈個(gè)體i所處的狀態(tài)和空間結(jié)構(gòu)有關(guān),后面部分則包含個(gè)體i與最近鄰j以及j的鄰居k間的相互作用.顯然,當(dāng)不存在懲罰時(shí),總收益差只與個(gè)體i和網(wǎng)絡(luò)結(jié)構(gòu)有關(guān).也就是說(shuō),懲罰的引入直接導(dǎo)致個(gè)體間產(chǎn)生相互作用.為了便于研究和分析,本文以二維正方格子上的公共物品博弈為例,展開(kāi)進(jìn)一步討論.在二維方格子中,ki=kj=4且∑j=4,表達(dá)式(8)中第一項(xiàng)可化簡(jiǎn)為Si［5?r?10(F?C)］,第二項(xiàng)中求和項(xiàng)是對(duì)所有與個(gè)體i相關(guān)的ki+1個(gè)集團(tuán)中所有的參與者進(jìn)行求和.圖2是對(duì)所有求和節(jié)點(diǎn)的求和次數(shù)的示意圖,可以將這樣的求和規(guī)則改寫(xiě)成:兩次最近鄰求和加上兩次次近鄰求和再加上一次第三近鄰求和,即其中j表示最近鄰,j′表示次近鄰,j′′表示第三近鄰.代入到(8)式的第二項(xiàng)可得:

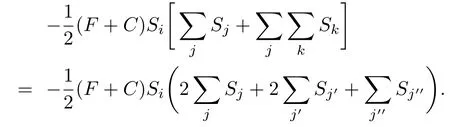
因此,表達(dá)式(8)可寫(xiě)成

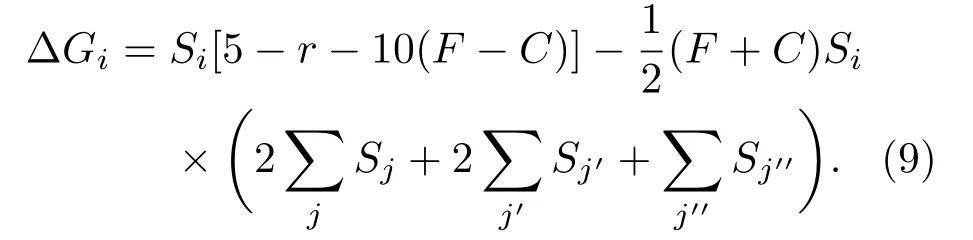
公共物品博弈中追求利益最大化,而Ising模型則希望系統(tǒng)能量達(dá)到最小.所以,定義有效能量差為?Ei=??Gi,相應(yīng)的,

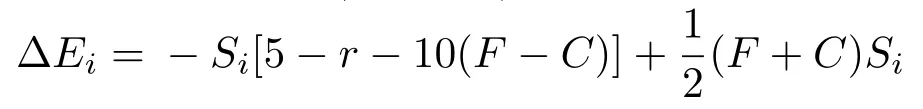
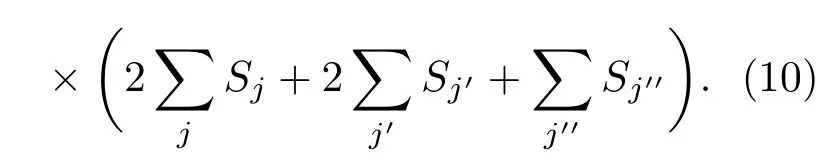
考慮最近鄰、次近鄰和第三近鄰的Ising模型的表達(dá)式為

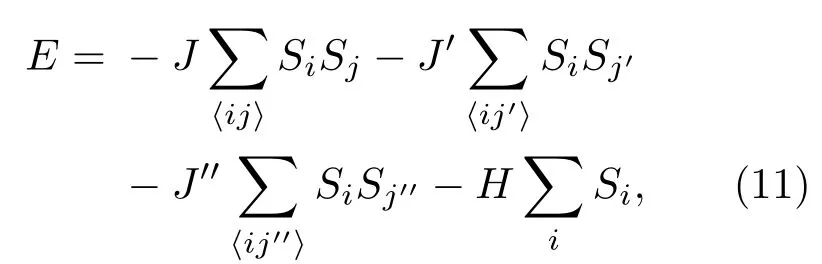
其中J表示最近鄰相互作用強(qiáng)度,J′表示次近鄰相互作用強(qiáng)度,J′′表示第三近鄰相互作用強(qiáng)度,〈ij〉表示對(duì)最近鄰求和,〈ij′〉表示對(duì)次近鄰求和,〈ij′′〉表示對(duì)第三近鄰求和,H表示外場(chǎng)強(qiáng)度.

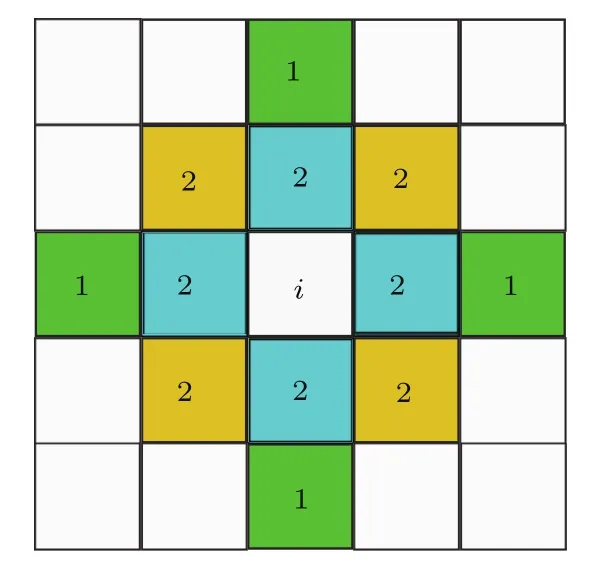
圖2 (網(wǎng)刊彩色)任意個(gè)體i參與的公共物品博弈等價(jià)于與最近次、次近鄰分別進(jìn)行兩次兩兩博弈和與第三近鄰進(jìn)行一次兩兩博弈Fig.2.(color online)The number of interaction between player i and it’s neighbours.

Ising模型的局部能量變化關(guān)系?E=E′?E可表示為

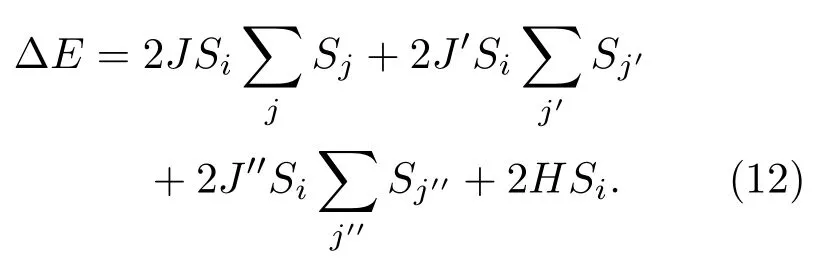
對(duì)比表達(dá)式(10)和表達(dá)式(12)可得公共物品博弈對(duì)應(yīng)類(lèi)Ising模型的耦合強(qiáng)度和外場(chǎng)為:

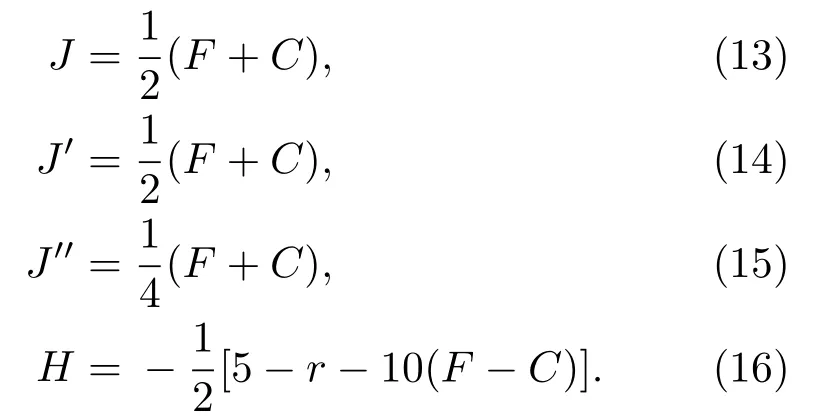
顯然,耦合強(qiáng)度是懲罰費(fèi)用和懲罰代價(jià)的函數(shù),因?yàn)镕＞0且C＞0,所以耦合強(qiáng)度J＞0.由Ising模型相關(guān)理論可知,該模型為鐵磁Ising模型.此外,耦合強(qiáng)度的大小與空間結(jié)構(gòu)和強(qiáng)化因子無(wú)關(guān),只與懲罰的取值相關(guān).外場(chǎng)由兩部分構(gòu)成:前一項(xiàng)表示一輪博弈中,均分后的利益是否大于原始投資;后一項(xiàng)來(lái)源于懲罰的引入,只要懲罰的費(fèi)用大于懲罰的代價(jià),外場(chǎng)都為正,即促進(jìn)合作的產(chǎn)生.特別指出,運(yùn)用矩陣分解法也可得到相似的等價(jià)關(guān)系［2］.

綜合寫(xiě)出有效能量為

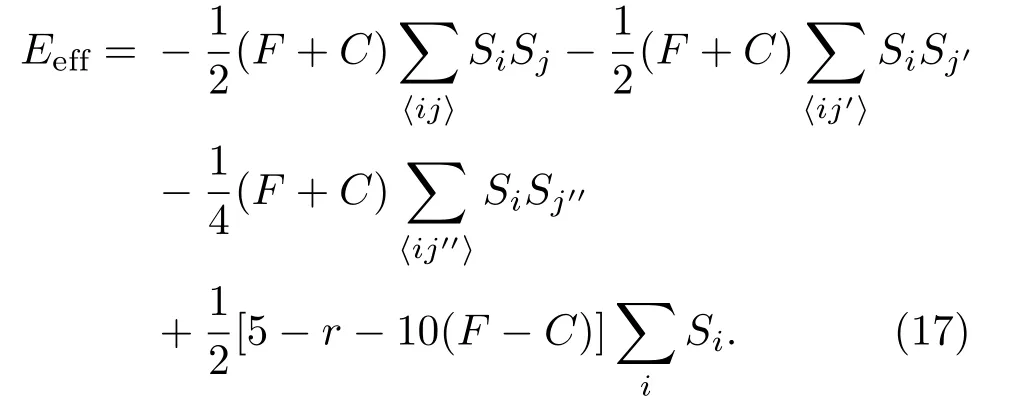
2.3 蒙特卡羅模擬

本部分采用Metropolis算法對(duì)周期邊界條件下二維空間正方格子上的公共物品博弈模型進(jìn)行蒙特卡羅模擬.空間格子的大小為N=L×L,用偽隨機(jī)數(shù)生成任意初始構(gòu)型后按照自我質(zhì)疑機(jī)制進(jìn)行演化.首先,隨機(jī)選擇群體中的任意博弈個(gè)體i,然后用自我質(zhì)疑機(jī)制決定個(gè)體i是否改變當(dāng)前策略,重復(fù)以上操作,直至系統(tǒng)趨于穩(wěn)定狀態(tài)為止.為了保證計(jì)算的準(zhǔn)確性,扔掉前10000個(gè)蒙特卡羅模步(N次隨機(jī)試驗(yàn)稱(chēng)為一個(gè)蒙特卡羅步).計(jì)算接下來(lái)的2×105個(gè)蒙特卡羅步的平均值.為消除初始條件對(duì)系統(tǒng)演化的影響,再選擇100個(gè)不同的初始構(gòu)型進(jìn)行系綜平均.

在演化博弈模型的社會(huì)學(xué)研究中,通常選擇合作者占比f(wàn)作為觀測(cè)量,其表達(dá)式為

其中N代表參與博弈的總?cè)藬?shù),N+代表總?cè)藬?shù)中采用合作策略的人數(shù).

由表達(dá)式(17)可知,當(dāng)不存在懲罰時(shí),耦合強(qiáng)度為零,體系的有效能量為

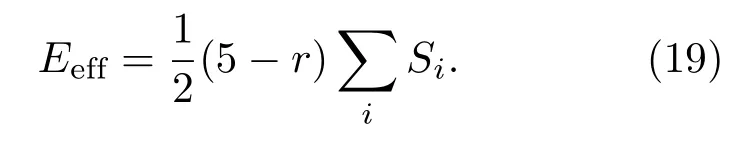
顯然,當(dāng)r＞5時(shí)為正向外場(chǎng),整個(gè)體系趨向于合作,而r＜5時(shí)為負(fù)向外場(chǎng),體系趨向于不合作.如圖3所示,合作與不合作以r=5為分界線,溫度較低時(shí),在強(qiáng)化因子逐漸增大的過(guò)程中,體系在r=5處,從完全不合作跳變到完全合作,隨著溫度的升高,這種跳變逐漸變得平緩.

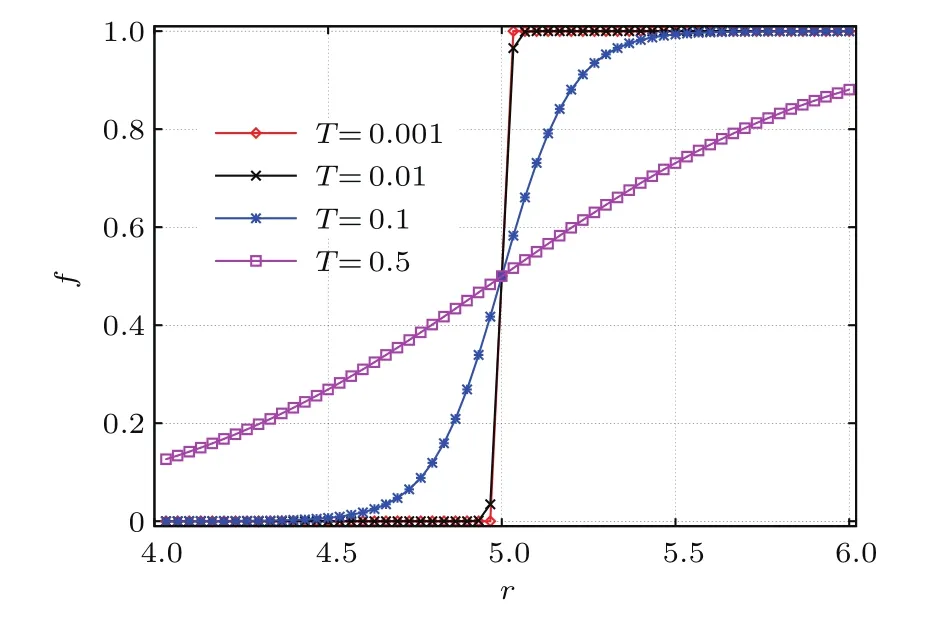
圖3 (網(wǎng)刊彩色)不存在懲罰時(shí)合作頻率隨強(qiáng)化因子的變化Fig.3.(color online)Frequency of cooperators vs.r for various T.

當(dāng)存在懲罰時(shí),體系表現(xiàn)為鐵磁相互作用,系統(tǒng)狀態(tài)隨外場(chǎng)而變.顯然,臨界外場(chǎng)Hc=0,即1?rc/5?2(F?C)=0.解得rc=5?10(F?C),則當(dāng)r＞rc時(shí),系統(tǒng)為完全合作狀態(tài),r＜rc時(shí)系統(tǒng)為完全不合作狀態(tài).圖4顯示不同的懲罰額度F和懲罰的代價(jià)C下,合作頻率f隨強(qiáng)化因子r的變化,固定溫度T=0.1.顯然,蒙特卡羅模擬的結(jié)果與Ising模型理論分析的結(jié)果很好地吻合.合作頻率以rc為突變點(diǎn)發(fā)生跳變.從社會(huì)學(xué)角度看,懲罰的引入增強(qiáng)了個(gè)體間的聯(lián)系,相應(yīng)地也增強(qiáng)了體系對(duì)不確定性因素T的魯棒性.

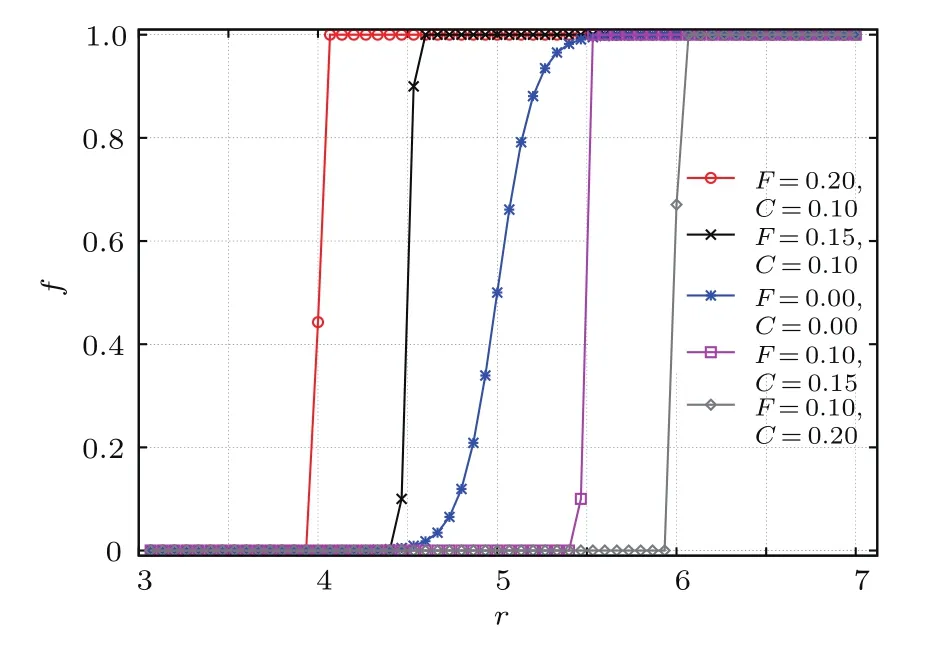
圖4 (網(wǎng)刊彩色)不同懲罰條件下合作頻率隨強(qiáng)化因子的變化Fig.4.(color online)Frequency of cooperators vs.r at T=0.1 for various punishment.

3 公共物品博弈模型的相變特性

從與公共物品博弈模型對(duì)應(yīng)的Ising模型中看到,耦合強(qiáng)度J恒大于零,體系表現(xiàn)為鐵磁相互作用.鐵磁Ising的相變和臨界現(xiàn)象在統(tǒng)計(jì)物理中已經(jīng)廣泛研究,基于判斷有效能量推導(dǎo)的正確性和解釋公共物品博弈誘發(fā)的相變現(xiàn)象兩個(gè)原因,我們采用蒙特卡羅模擬和有限尺度標(biāo)度理論詳細(xì)分析公共物品博弈模型的相變特性.在Ising模型中,零場(chǎng)下隨著溫度的變化,存在鐵磁序到順磁序的二級(jí)相變(即由完全合作或完全不合作態(tài)向混亂狀態(tài)的轉(zhuǎn)變),相變溫度稱(chēng)為臨界溫度,在臨界溫度附近表現(xiàn)出標(biāo)度特性;外場(chǎng)非零時(shí),只要溫度小于臨界溫度,隨著外場(chǎng)的變化會(huì)引發(fā)一級(jí)相變(由完全合作態(tài)到完全不合作態(tài)的轉(zhuǎn)變或其逆過(guò)程).為了便于與Ising模型進(jìn)行對(duì)比,本部分仍采用Ising模型的相關(guān)觀測(cè)量展開(kāi)研究,即選擇磁化強(qiáng)度(magnetization)作為序參量.其表達(dá)式為

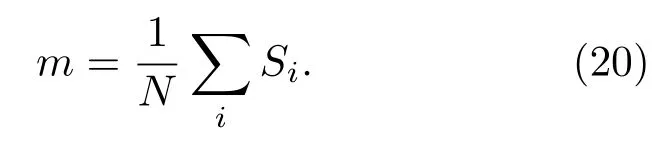
磁化強(qiáng)度與合作者占比的關(guān)系為m=2f?1.此外,定義磁化率為

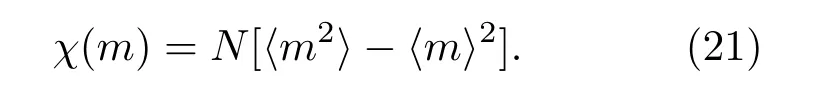
一級(jí)相變和二級(jí)相變具有完全不同的相變特性,如二級(jí)相變由于關(guān)聯(lián)長(zhǎng)度的發(fā)散引發(fā)一系列奇異特性而一級(jí)相變則表現(xiàn)出δ函數(shù)奇異性.為了討論方便,先簡(jiǎn)單介紹一級(jí)相變和二級(jí)相變的標(biāo)度函數(shù),然后再進(jìn)行蒙特卡羅模擬.

二級(jí)相變的相變點(diǎn)通常稱(chēng)為臨界點(diǎn),在臨界點(diǎn)附近,系統(tǒng)的關(guān)聯(lián)長(zhǎng)度發(fā)散,從而引起系統(tǒng)相關(guān)熱力學(xué)量的奇異性,如比熱和磁化率在臨界點(diǎn)處發(fā)散.通常無(wú)窮大系統(tǒng)才表現(xiàn)出臨界現(xiàn)象,然而無(wú)論是實(shí)際系統(tǒng)還是計(jì)算機(jī)模擬都不可能無(wú)窮大.Fisher于20世紀(jì)70年代提出的有限尺度標(biāo)度理論通過(guò)對(duì)小系統(tǒng)的計(jì)算機(jī)模擬實(shí)現(xiàn)了對(duì)臨界現(xiàn)象的研究［32］.具體而言,在臨界點(diǎn)附近磁化強(qiáng)度和磁化率存在以下標(biāo)度關(guān)系:

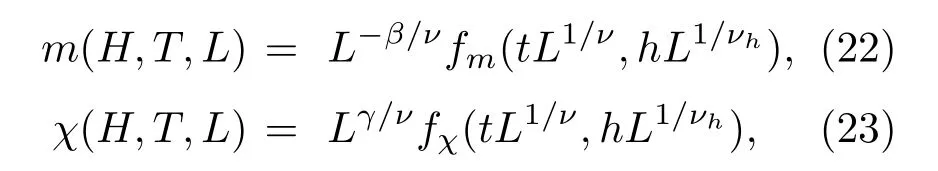
其中,fm和fχ為普適函數(shù),t=(T?Tc)/Tc和h=(H?Hc)/Hc分別稱(chēng)為約化溫度和約化外場(chǎng),L是有限系統(tǒng)的特征長(zhǎng)度,ν和νh分別代表關(guān)聯(lián)長(zhǎng)度對(duì)溫度和外場(chǎng)發(fā)散的臨界指數(shù),1/νh=(γ+β)/ν,β和γ是描述熱力學(xué)函數(shù)m和χ臨界行為的臨界指數(shù).為確定臨界點(diǎn)的位置,定義四階Binder累積量為

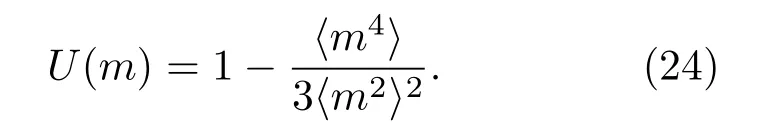
Binder累計(jì)量的標(biāo)度形式滿足

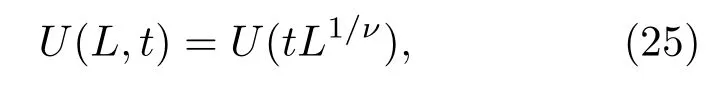
其中U為普適函數(shù),在臨界點(diǎn)處,它與系統(tǒng)尺寸無(wú)關(guān),即不同尺度下U的曲線交于臨界點(diǎn).

在無(wú)窮大系統(tǒng)中,一級(jí)相變的關(guān)聯(lián)長(zhǎng)度不發(fā)散且相變表現(xiàn)為δ函數(shù)奇異性,即磁化率可用一個(gè)δ函數(shù)表示.但在有限系統(tǒng)模擬中,δ函數(shù)的奇異性將被平滑掉.文獻(xiàn)［33—37］運(yùn)用熱力學(xué)漲落理論獲得了一級(jí)相變磁化強(qiáng)度、磁化率和四階累積量的有限尺度標(biāo)度函數(shù).磁化強(qiáng)度為

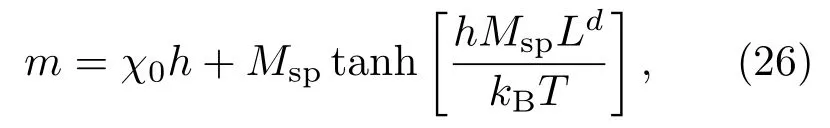
其中Msp是熱力學(xué)極限下的自發(fā)磁化強(qiáng)度,χ0是系統(tǒng)處于單相時(shí)的磁化率,d為系統(tǒng)維度,kB表示玻爾茲曼常數(shù).

磁化率為

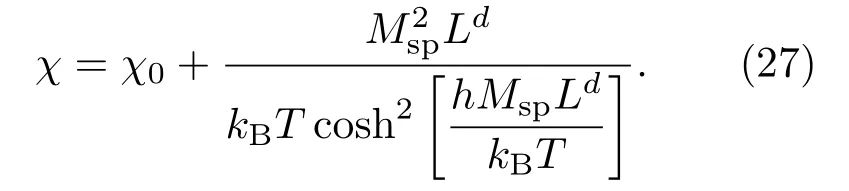
上式表明,在L→∞極限下發(fā)生在H=0處的δ函數(shù)奇異性,當(dāng)L有限時(shí)被平滑為一個(gè)峰,其高度正比于Ld,其寬度正比于L?d.

四階累計(jì)量的表達(dá)式為

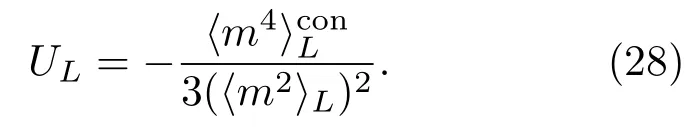
從磁化強(qiáng)度、磁化率和四階累計(jì)量的表達(dá)式看出,空間維度d是一級(jí)相變的唯一標(biāo)度指數(shù).

3.1 外場(chǎng)為零時(shí)的相變特性

公共物品博弈對(duì)應(yīng)的有效能量包括:最近鄰、次近鄰和第三近鄰相互作用,精確解未知.外場(chǎng)為零時(shí),體系隨溫度變化表現(xiàn)為二級(jí)相變,通過(guò)四階Binder累積量可以確定臨界溫度的位置,通過(guò)有限尺度標(biāo)度理論可以獲得相應(yīng)的臨界指數(shù).模擬過(guò)程中,固定懲罰額度F=0.2,懲罰費(fèi)用C=0.1,此時(shí)外場(chǎng)h=(r?4)/2.顯然,當(dāng)r＞4時(shí),h＞0為正向外場(chǎng),r＜4時(shí),為負(fù)向外場(chǎng),r=4時(shí),外場(chǎng)為零.為研究的方便,先研究外場(chǎng)為零時(shí)系統(tǒng)隨溫度變化表現(xiàn)出的二級(jí)相變.

圖5和圖6是零外場(chǎng)時(shí)磁化強(qiáng)度和磁化率隨溫度變化的曲線,顯然,不同尺寸下存在顯著的有限尺度效應(yīng).磁化強(qiáng)度隨著系統(tǒng)尺寸的增大,臨界點(diǎn)附近的曲線變得越來(lái)越陡,越來(lái)越接近系統(tǒng)無(wú)窮大時(shí)的變化規(guī)律.熱力學(xué)極限下,磁化率在臨界點(diǎn)處發(fā)散,但在有限系統(tǒng)下為有限值,圖6正好說(shuō)明了這一點(diǎn),隨著系統(tǒng)尺度的不斷增大,曲線的峰值變得越來(lái)越大.

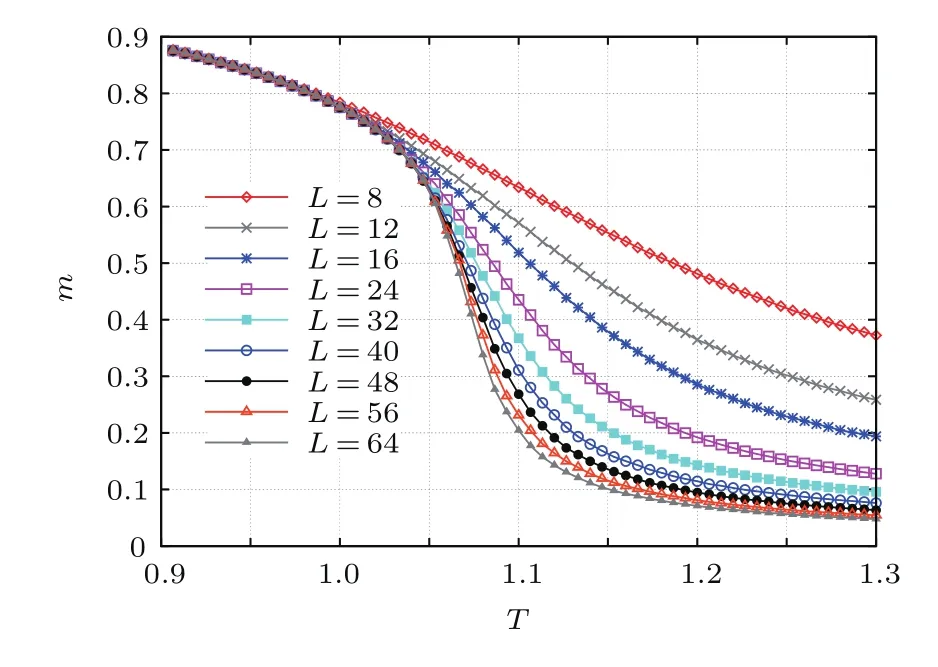
圖5 (網(wǎng)刊彩色)外場(chǎng)為零時(shí)不同尺度下磁化強(qiáng)度隨溫度的變化Fig.5.(color online)Magnetization m plotted vs temperature T at h=0 for various L.

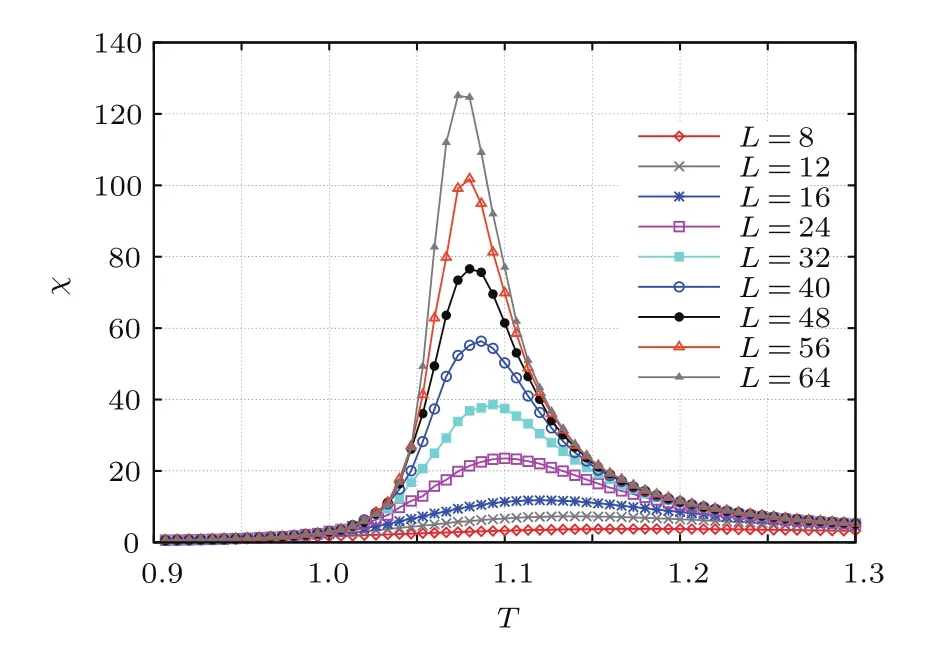
圖6 (網(wǎng)刊彩色)外場(chǎng)為零時(shí)不同尺度下磁化率隨溫度的變化Fig.6.(color online)Susceptibility χLplotted vs temperature T at h=0 for various L.

不同尺寸下的Binder累積量曲線相交于臨界溫度. 如圖7所示,可確定臨界溫度Tc=1.065±0.0067.通過(guò)有限尺度標(biāo)度理論,可以測(cè)定臨界指數(shù)β/ν=0.154±0.0042,γ/ν=1.71±0.023,1/ν=1.085±0.027.將模擬結(jié)果與二維Ising模型的精確值對(duì)比,發(fā)現(xiàn)二者的臨界指數(shù)存在一定差異,有可能是普適類(lèi)發(fā)生了變化.為了進(jìn)一步驗(yàn)證我們的設(shè)想,圖8和圖9用二維Ising模型的臨界指數(shù)去坍塌模擬所得數(shù)據(jù).可以明顯看到臨界點(diǎn)右半邊曲線的坍塌效果較差,導(dǎo)致這一現(xiàn)象的原因是博弈模型中不僅包含最近鄰相互作用,還包括次近鄰和第三近鄰相互作用.

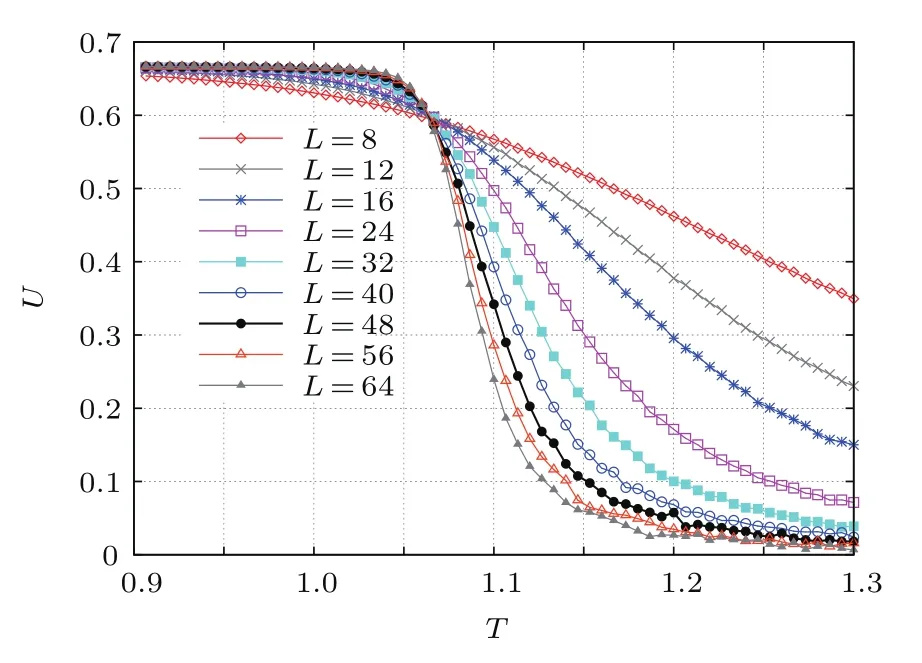
圖7 (網(wǎng)刊彩色)外場(chǎng)為零時(shí)不同系統(tǒng)尺度下四階累積量隨溫度的變化Fig.7.(color online)Reduced cumulant U plotted vs temperature T at h=0 for various L.

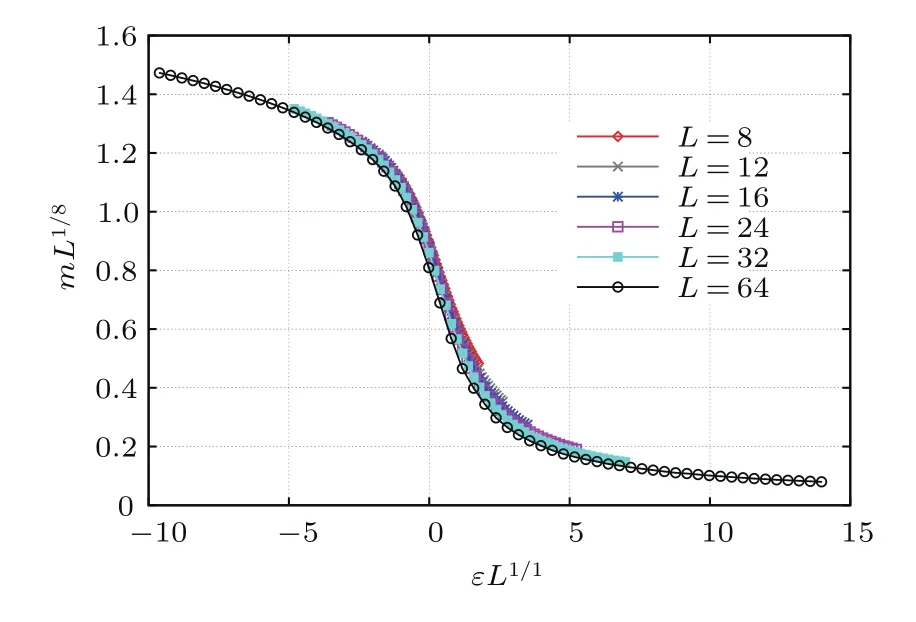
圖8 (網(wǎng)刊彩色)外場(chǎng)為零時(shí)臨界溫度附近磁化強(qiáng)度的有限尺度標(biāo)度關(guān)系Fig.8. (color online)Scaled magnetization mL1/8 plotted vs scaled temperature εL1/1at T=1.065 and various L.

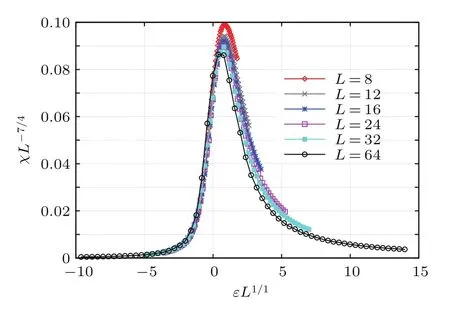
圖9 (網(wǎng)刊彩色)外場(chǎng)為零時(shí)臨界溫度附近磁化率的有限尺度標(biāo)度關(guān)系Fig.9.(color online)Scaled susceptibility χL/L7/4 plotted vs scaled temperature εL1/1at T=1.065 and various L.

3.2 外場(chǎng)非零時(shí)的相變特性

當(dāng)溫度小于臨界溫度時(shí),沿外場(chǎng)演化模型表現(xiàn)為一級(jí)相變.當(dāng)溫度等于臨界溫度時(shí),表現(xiàn)為二級(jí)相變.為更好地對(duì)比和區(qū)分兩種相變,分別討論T=1(T＜Tc,一級(jí)相變)和T=1.065(T=Tc,二級(jí)相變)兩種情況.

圖10和圖11分別為T(mén)=1和T=1.065時(shí)磁化強(qiáng)度隨外場(chǎng)的變化曲線.當(dāng)系統(tǒng)無(wú)窮大時(shí),在相變點(diǎn)r=5處,磁化強(qiáng)度不連續(xù),發(fā)生跳變.當(dāng)系統(tǒng)尺寸有限時(shí),磁化強(qiáng)度曲線的奇異性被平滑掉.隨著系統(tǒng)尺寸的不斷增大,曲線變得越來(lái)越陡峭,系統(tǒng)無(wú)窮大時(shí)變得不連續(xù).對(duì)比兩圖發(fā)現(xiàn):在rc附近,T=Tc處磁化強(qiáng)度的變化比T＜Tc處的變化要緩慢一些.

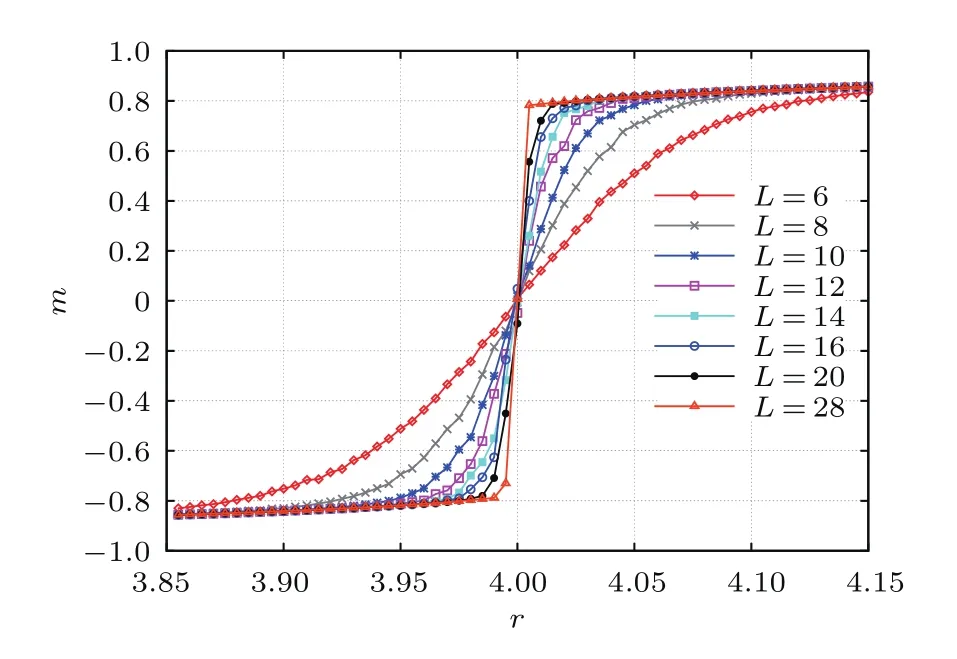
圖10 (網(wǎng)刊彩色)T＜Tc時(shí)不同尺度下磁化強(qiáng)度隨強(qiáng)化因子的變化Fig.10.(color online)Magnetization m plotted vs the factor r at T=1 for various L.

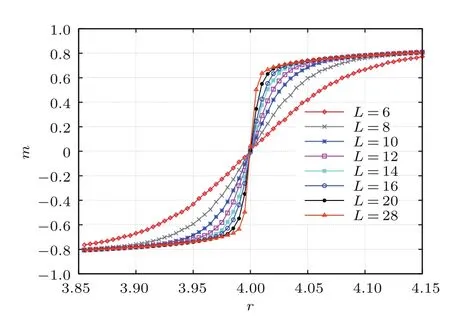
圖11 (網(wǎng)刊彩色)T=Tc時(shí)不同尺度下磁化強(qiáng)度隨強(qiáng)化因子的變化Fig.11.(color online)Magnetization m plotted vs the factor r at T=1.065 for various L.

圖12和圖13分別展示了T=1和T=1.065時(shí)磁化率隨外場(chǎng)的變化曲線.從(27)式知道,磁化率在相變點(diǎn)處隨系統(tǒng)尺寸冪率發(fā)散,在兩圖中可以明顯看到,隨著系統(tǒng)尺度的增大,磁化率曲線的尖峰不斷增大,當(dāng)系統(tǒng)尺度為無(wú)窮大時(shí)發(fā)散,T=Tc處的峰值沒(méi)有T＜Tc處的峰值高.這是由于系統(tǒng)無(wú)窮大時(shí),一級(jí)相變?cè)谂R界點(diǎn)附近δ函數(shù)發(fā)散而二級(jí)相變則按臨界指數(shù)γ冪率發(fā)散.

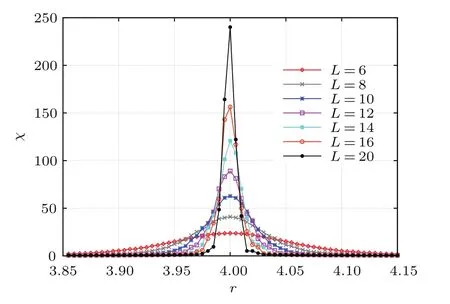
圖12 (網(wǎng)刊彩色)T＜Tc時(shí)不同尺度下磁化率隨強(qiáng)化因子的變化Fig.12.(color online)Susceptibility χLplotted vs the factor r at T=1 for various L.

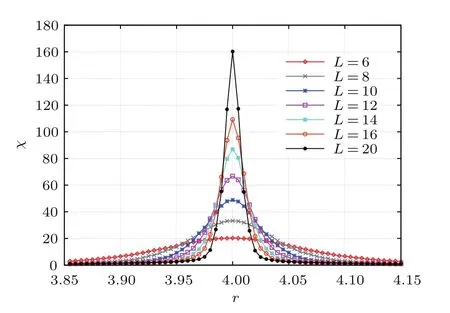
圖13 (網(wǎng)刊彩色)T=Tc時(shí)不同尺度下磁化率隨強(qiáng)化因子的變化Fig.13.(color online)Susceptibility χLplotted vs the factor r at T=1.065 for various L.

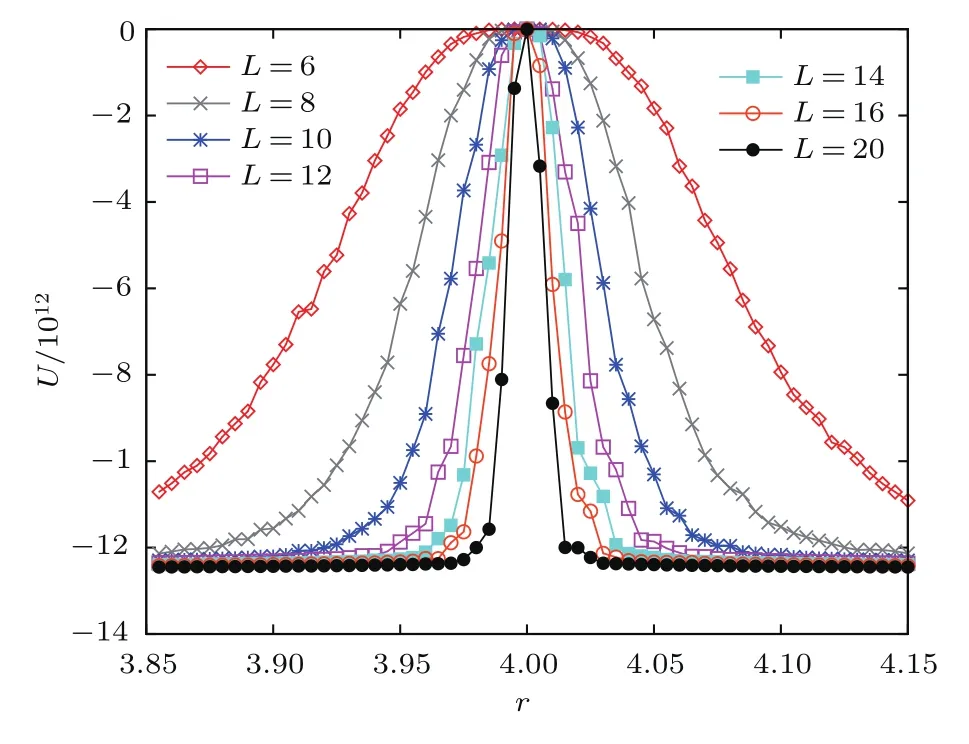
圖14 (網(wǎng)刊彩色)T＜Tc時(shí)不同尺度下四階累積量隨強(qiáng)化因子的變化Fig.14.(color online)Reduced cumulant U plotted vs the factor r at T=1 for various L.

圖14和圖15得到了公共物品博弈相變點(diǎn)的位置,可明顯看到不同尺度下所有曲線都交于相變點(diǎn)r=4處.

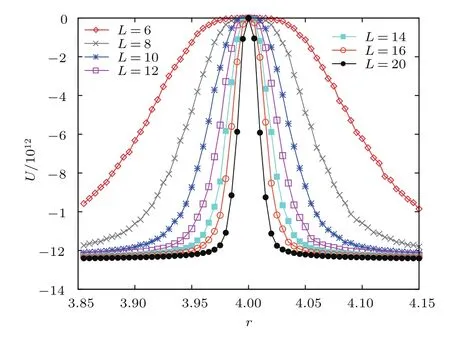
圖15 (網(wǎng)刊彩色)T=Tc時(shí)不同尺度下四階累積量隨強(qiáng)化因子的變化Fig.15.(color online)Reduced cumulant U plotted vs the factor r at T=1.065 for various L.

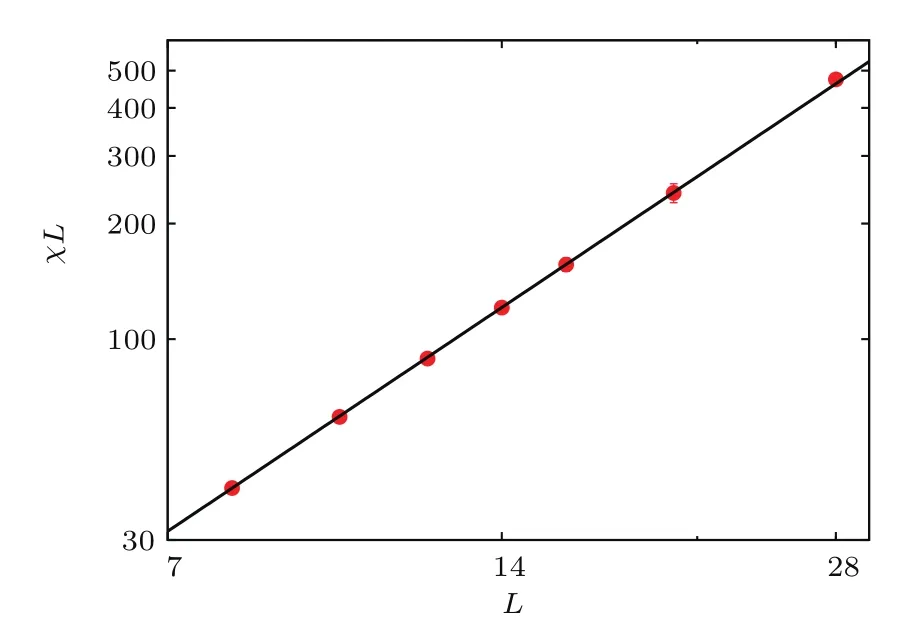
圖16 (網(wǎng)刊彩色)T＜Tc時(shí)臨界外場(chǎng)處磁化率隨尺度變化的雙對(duì)數(shù)圖Fig.16.(color online)Log-log plot of susceptibility maximum vs linear dimension at T=1.

圖16和圖17為磁化率隨系統(tǒng)變化的雙對(duì)數(shù)曲線,擬合曲線的斜率可以獲得磁化率隨尺度變化的臨界指數(shù),當(dāng)T＜Tc時(shí)臨界指數(shù)d=1.935±0.0093;當(dāng)T=Tc時(shí),臨界指數(shù)γ/ν=1.714±0.0026.二維Ising模型臨界指數(shù)的精確結(jié)果為d=2和γ/ν=1.75.顯然二者間仍然有微小的差別,為了進(jìn)一步驗(yàn)證模擬結(jié)果的正確性,圖18和圖19用二維Ising模型的臨界指數(shù)對(duì)模擬所得數(shù)據(jù)進(jìn)行坍塌,其中ε=(r?rc)/rc為約化增益系數(shù),γ/ν的理論值為7/4,(γ+β)/ν的理論值為15/8.圖16基于表達(dá)式(27)進(jìn)行數(shù)據(jù)坍塌,在坍塌過(guò)程中忽略修正項(xiàng)χ0.從圖中可以看出,公共物品博弈模型隨外場(chǎng)變化的相變特性和二維Ising模型完全相同.

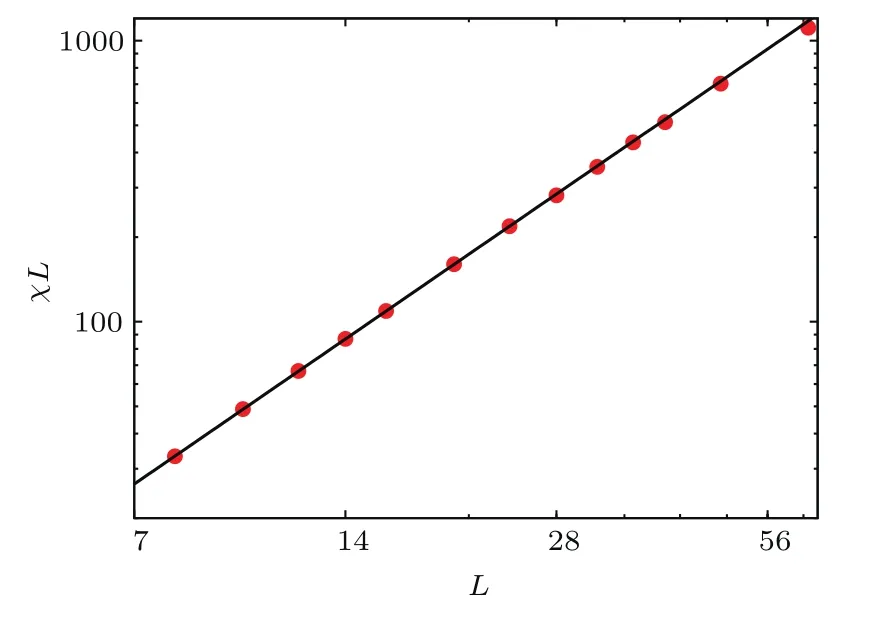
圖17 (網(wǎng)刊彩色)T=Tc時(shí)臨界外場(chǎng)處磁化率隨尺度變化的雙對(duì)數(shù)圖Fig.17.(color online)Log-log plot of susceptibility maximum vs linear dimension at T=1.065.

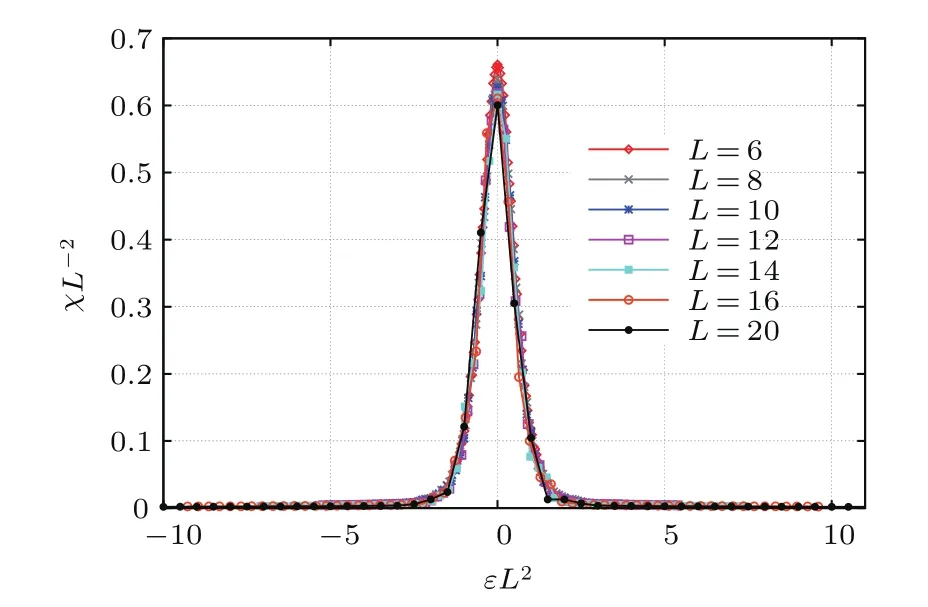
圖18 (網(wǎng)刊彩色)T＜Tc時(shí)臨界外場(chǎng)附近磁化率的有限尺度標(biāo)度關(guān)系Fig.18. (color online)Scaled susceptibility χL/L2 plotted vs scaled fi eld εL2at T=1 and various L.

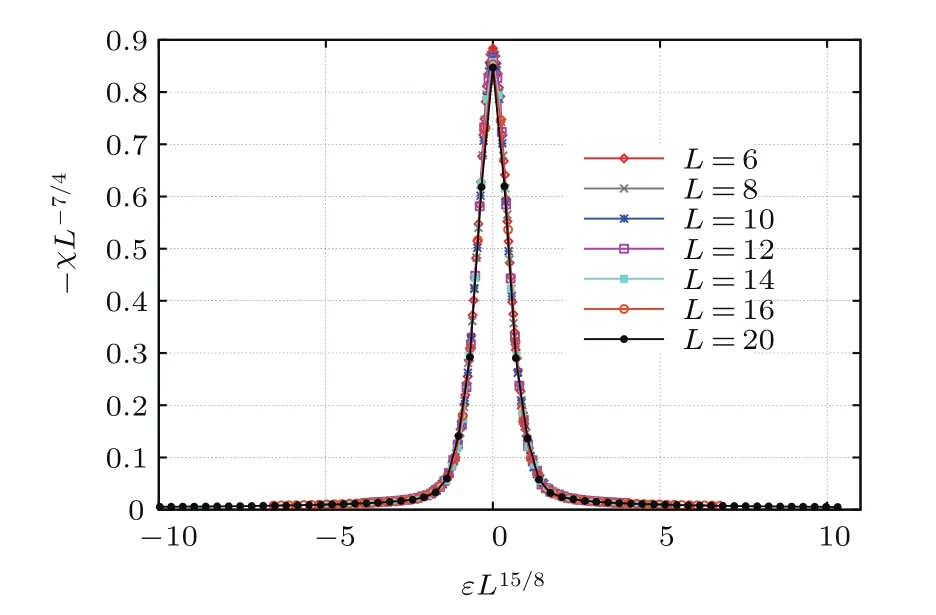
圖19 (網(wǎng)刊彩色)T=Tc時(shí)臨界外場(chǎng)附近磁化率的有限尺度標(biāo)度關(guān)系Fig.19.(color online)Scaled susceptibility χL/L7/4plotted vs scaled fi eld εL15/8at T=1.065 and various L.

圖20和圖21用臨界指數(shù)的精確解對(duì)模擬得到的磁化強(qiáng)度的數(shù)據(jù)進(jìn)行了坍塌.T＜Tc時(shí),圖20顯示,在臨界點(diǎn)rc附近曲線的坍塌效果較好,隨著r逐漸遠(yuǎn)離rc,坍塌效果變差.其原因來(lái)源于表達(dá)式(26),在rc附近m≈hMspL2kBT.圖21顯示了較好的坍塌效果.

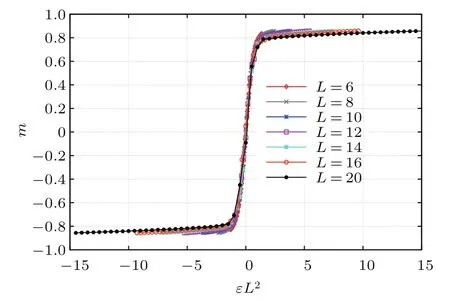
圖20 (網(wǎng)刊彩色)T＜Tc時(shí)臨界外場(chǎng)附近磁化強(qiáng)度的有限尺度標(biāo)度關(guān)系Fig.20.(color online)Scaled magnetization m plotted vs scaled fi eld εL2at T=1 and various L.

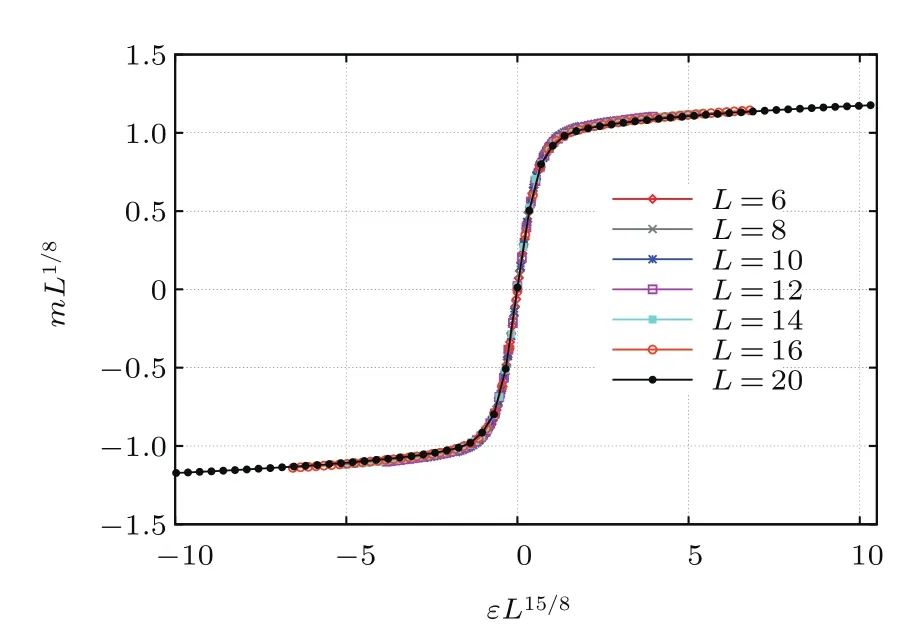
圖21 (網(wǎng)刊彩色)T=Tc時(shí)臨界外場(chǎng)附近磁化強(qiáng)度的有限尺度標(biāo)度關(guān)系Fig.21.(color online)Scaled magnetization mL1/8 plotted vs scaled fi eld εL15/8at T=1.065 and various L.

4 結(jié) 論

本文研究了有償懲罰機(jī)制下隨自我質(zhì)疑更新規(guī)則演化的公共物品博弈模型.首先采用博弈模型收益差類(lèi)比Ising模型能量差的方法,獲得了二維正方格子上博弈模型的有效能量.有效能量顯示:沒(méi)有懲罰時(shí),個(gè)體間不存在相互作用,合作策略的選取只與外場(chǎng)有關(guān),外場(chǎng)則取決于原始投資和最終獲得收益分紅間的關(guān)系;存在懲罰時(shí),個(gè)體間包括最近鄰、次近鄰和第三近鄰相互作用,同時(shí)也減小了外場(chǎng)的作用(懲罰需要付出代價(jià)).也就是說(shuō),懲罰的引入增強(qiáng)了個(gè)體間的關(guān)聯(lián),促使博弈群體具有更強(qiáng)的魯棒性,微小的擾動(dòng)很難引起個(gè)體策略的改變.其次,計(jì)算機(jī)模擬博弈過(guò)程獲得了不同理性程度和不同懲罰額度下合作者占比的變化曲線.結(jié)果顯示:模擬結(jié)果和類(lèi)Ising分析結(jié)果完全吻合.最后,以Ising模型相關(guān)的熱力學(xué)量為基礎(chǔ)研究了公共物品博弈模型的相變和臨界現(xiàn)象.分別對(duì)二級(jí)相變和一級(jí)相變進(jìn)行了討論,結(jié)果顯示,公共物品博弈模型隨理性參數(shù)演化的二級(jí)相變與鐵磁Ising模型隨溫度變化的二級(jí)相變不同,而一級(jí)相變則具有相同的有限尺度效應(yīng).需要特別說(shuō)明的是,公共物品博弈通過(guò)集體分紅獲得收益,而傳統(tǒng)的囚徒困境和雪堆博弈通過(guò)兩兩相互博弈獲得收益.雖然二者的博弈形式不同,但都可以轉(zhuǎn)化為與之等價(jià)的Ising模型,囚徒困境和雪堆博弈對(duì)應(yīng)的Ising模型已經(jīng)在參考文獻(xiàn)［28］中給出.

［1］Szabó G,Fath G 2007Phys.Rep.446 97

［2］Szabó G,Borsos I 2016Phys.Rep.624 1

［3］He D R,Liu Z H,Wang B H 2009Complex Systems and Complex Networks(Beijing:Higher Education Press)p73(in Chinese)［何大韌,劉宗華,汪秉宏 2009復(fù)雜系統(tǒng)與復(fù)雜網(wǎng)絡(luò)(北京:高等教育出版社)第73頁(yè)］

［4］Nowak M A 2006Science314 1560

［5］Nowak M A,May R M 1992Nature359 826

［6］Nowak M A(translated by Li Z Q,Wang S C)2010Evolutionary Dynamics:Exploring the Equations of Life(Beijing:Higher Education Press)pp108–125(in Chinese)［Martin A.Nowak著 (李振清,王世暢 譯)2010進(jìn)化動(dòng)力學(xué)-探索生命的方程(北京：高等教育出版社)第108—125頁(yè)］

［7］Hardin G 1968Science162 1243

［8］Feeny D,Berkes F,McCay B J,Acheson J M 1990Hum.Ecol.18 1

［9］Palfrey T R,Rosenthal H 1984J.Public Econ.24 171

［10］Wang X W 2015M.D.Dissertation(Anhui:University of Science and Technology of China)(in Chinese)［王旭文2015博士學(xué)位論文(安徽:中國(guó)科學(xué)技術(shù)大學(xué))］

［11］Wang B K 2013M.S.Dissertation(Xi’an:Xidian University)(in Chinese)［王保魁 2013碩士學(xué)位論文 (西安:西安電子科技大學(xué))］

［12］Gao J 2012Ph.D.Dissertation(Xi’an:Xidian University)(in Chinese)［高佳 2012博士學(xué)位論文 (西安:西安電子科技大學(xué))］

［13］Hauert C,Traulsen A,Brandt H,Nowak M A,Sigmund K 2007Science316 1905

［14］Dreber A,Rand D G,Fudenberg D,Nowak M A 2008Nature452 348

［15］Helbing D,Szolnoki A,Perc M,Szabó G 2010New J.Phys.12 083005

［16］Helbing D,Szolnoki A,Perc M,Szabó G 2010Phys.Rev.E81 057104

［17］Ohtsuki H,Iwasa Y,Nowak M A 2009Nature457 79

［18］Szolnoki A,Szabó G,Perc M2011Phys.Rev.E83 036101

［19］Hauert C,Doebeli M 2004Nature428 643

［20］Santos F C,Santos M D,Pacheco J M 2008Nature454 213

［21］Szabó G,T?ke C 1998Phys.Rev.E58 69

［22］Szabó G,Hauert C 2002Phys.Rev.Lett.89 118101

［23］Szabó G,Vukov J,Szolnoki A 2005Phys.Rev.E72 047107

［24］Wang W X,Ren J,Chen G,Wang B H 2006Phys.Rev.E74 056113

［25］Gao K,Wang W X,Wang B H 2007Physica A380 528

［26］Liu Y K,Li Z,Chen X J,Wang L 2009Chin.Phys.Lett.26 377

［27］Liu Y K 2010Ph.D.Dissertation(Xi’an:Xidian University)(in Chinese)［劉永奎 2010博士學(xué)位論文 (西安:西安電子科技大學(xué))］

［28］Yang B,Li X T,Chen W,Liu J,Chen X S 2016Commun.Theor.Phys.66 439

［29］McKelvey R D,Palfrey T R 1995Games Econ.Behav.10 6

［30］He J T 2006Behavioral Economics The Economic Behavior of China(Beijing:China Financial Economic Publishing House)p79(in Chinese)［賀京同 2006行為經(jīng)濟(jì)學(xué)與中國(guó)經(jīng)濟(jì)行為(北京:中國(guó)財(cái)政經(jīng)濟(jì)出版社)第79頁(yè)］

［31］Zhuang Q,Di Z R,Wu J S 2014PloS One9 e105391

［32］Fisher M E 1967Rep.Prog.Phys.30 615

［33］Privman V 1990Finite Size Scaling and Numerical Simulation of Statistical Systems(Singapore:World Scienti fi c)p223

［34］Landau D P,Binder K 2014A Guide to Monte Carlo Simulations in Statistical Physics(United Kingdom:Cambridge University Press)p82

［35］Binder K,Heermann D 2010Monte Carlo Simulation in Statistical Physics An Introduction(Berlin Heidelberg:Springer-Verlag)p56

［36］Binder K,Landau D P 1984Phys.Rev.B30 1477

［37］Lee J,Kosterlitz J M 1991Phys.Rev.B43 3265

Phase transition properties for the spatial public goods game with self-questioning mechanism?

Yang Bo1)2)?Fan Min1)2)Liu Wen-Qi1)2)Chen Xiao-Song3)4)
1)(Data Science Research Center,Kunming University of Science and Technology,Kunming 650500,China)
2)(Faculty of Science,Kunming University of Science and Technology,Kunming 650500,China)
3)(Institute of Theoretical Physics,Key Laboratory of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China)
4)(School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China)

The spatial public goods game is one of the most popular models for studying the emergence and maintenance of cooperation among sel fi sh individuals.A public goods game with costly punishment and self-questioning updating mechanism is studied in this paper.The theoretical analysis and Monte Carlo simulation are involved to analyze this model.This game model can be transformed into Ising model with an external fi eld by theoretical analysis.When the costly punishment exists,the e ff ective Hamiltonian includes the nearest-,the next-nearest-and the third-nearestneighbor interactions and non-zero external fi eld.The interactions are only determined by costly punishment.The sign of the interaction is always greater than zero,so it has the properties of ferromagnetic Ising.The external fi eld is determined by the factorrof the public goods game,the fi neFon each defector within the group,and the relevant punishment costC.The Monte Carlo simulation results are consistent with the theoretical analysis results.In addition,the phase transitions and critical behaviors of the public goods game are also studied using the fi nite size scaling theory.The results show that the discontinuous phase transition has the same fi nite size e ff ects as the two-dimensional Ising model,but the continuous phase transitions is inconsistent with Ising model.

ising model, fi nite size scaling theory,Monte Carlo simulations,self-questioning update rules

27 May 2017;revised manuscript

4 July 2017)

(2017年5月27日收到;2017年7月4日收到修改稿)

10.7498/aps.66.196401

?昆明理工大學(xué)引進(jìn)人才科研啟動(dòng)基金項(xiàng)目(批準(zhǔn)號(hào)：KKSY201607047)和國(guó)家自然科學(xué)基金(批準(zhǔn)號(hào):61573173)資助的課題.

?通信作者.E-mail:yangbo@kmust.edu.cn

?2017中國(guó)物理學(xué)會(huì)Chinese Physical Society

PACS:64.60.De,87.55.K–,02.50.Le,87.23.Ge

10.7498/aps.66.196401

*Scienti fi c Research Foundation for Introduced Scholars,Kunming University of Science and Technology(Grant No.KKSY201607047)and the National Natural Science Foundation of China(Grant No.61573173).

?Corresponding author.E-mail:yangbo@kmust.edu.cn