偏光全息研究歷程與展望

洪一凡，臧金亮，劉 穎，范鳳蘭，吳安安，邵 龍，康果果*，譚小地

(1.北京理工大學 光電學院 信息光學研究室，北京 100081；2.日本東京大學 生產技術研究所，東京 153-8505)

偏光全息研究歷程與展望

洪一凡1，臧金亮1，劉 穎1，范鳳蘭1，吳安安2，邵 龍1，康果果1*，譚小地1

(1.北京理工大學 光電學院 信息光學研究室，北京 100081；2.日本東京大學 生產技術研究所，東京 153-8505)

全息是目前一項極具前景的科學技術，即通過信號光和參考光的干涉，在小小的全息圖上記錄豐富的信息。相比于傳統全息僅記錄光波的相位、振幅信息，偏光全息可以將額外的偏振信息記錄于偏振態敏感材料中。本文從偏光全息材料入手，詳細介紹了偏光全息生產過程；同時介紹基于瓊斯理論和張量理論的偏光全息原理和研究進展；最后描述了偏光全息在全息存儲和納米光學領域的發展前景。

偏光全息；瓊斯理論；張量理論；偏振態

1 引 言

全息是一種利用光的干涉原理記錄光波干涉條紋，再利用光的衍射，再現記錄光波的全部信息的技術[1]。全息術的發展可分為3個階段：第一階段是從全息術的首次提出到20世紀50年代末期。該階段的標志性成果有同軸全息的出現和建立了全息術的基本理論。然而由于光源的限制(多為汞燈)，和參考光波與物光波的共軸(±1級衍級不能分開)，使得該階段的全息術并沒有獲得理想的實驗效果。第二階段開始于20世紀60年代，其標志性成果有：(1)1962年，Upatnieks、Leith發明離軸全息技術。其原理特性解決了孿生像的問題[2]；(2)同年，Denisyuk發明反射式體積全息圖[3]，并通過白光重建了記錄的物光波；(3)1963年，Vander Lugh發明了全息復空間濾波器[4]；(4)1969年，S.Benton發明了彩虹全息圖技術[5]。在這一階段，全息技術在顯示、干涉測量中都有了很多的應用[6-8]。第三階段開始于21世紀。隨著計算機技術的大規模應用，全息技術、光電子技術以及非線性光學技術通過計算機技術緊密地結合了起來，在全息技術領域取得了一系列突破性的進展和矚目的成就[9-10]。

光波作為一種電磁波，是橫波，也就是說它的光矢量的振動方向始終垂直與光波的傳播方向。人們把光矢量振動方向與光波傳播方向的不對稱性稱為偏振，偏振是橫波獨有的特性。光波按偏振狀態可分為：自然光、完全偏振光、部分偏振光。自然光也可以稱為非偏振光，指的是在垂直于光波傳播的平面上光矢量的取向有著均勻概率分布，而其大小和方向呈現無規則的變化。但在統計學的角度上看，自然光的振動方向又是對稱的，其分布于整個振動平面且各方向上強度都是相同的。完全偏振光是指光波矢量的大小和方向在光波傳播過程中都呈現有規律變化的或者保持不變的。完全偏振光依照其變化規律又可以被分為線偏振光、圓偏振光和橢圓偏振光。其中線偏振光是指在傳播過程中，光矢量的振動方向維持一致，它的端點軌跡是一條直線，而其光矢量的大小隨著相位而變化。圓偏振光是指光波它的光矢量的大小在傳播過程中保持不變，而其振動方向不斷變化，最終端點軌跡呈現正圓形。橢圓偏振光是指光波光矢量的大小和方向在傳播過程中都是按一定的規律變化，其端點呈現的軌跡是橢圓形。部分偏振光可以理解為完全偏振光與自然光的疊加。

偏振是光的3個特性之一，但是由于偏振的高精度測量、控制和再現還沒有很好的解決，人們對它的應用與振幅和相位相比還很不夠。例如人眼或COMS、CCD等光電器件都是對振幅成像，也就說光的振幅最易被人們觀測，因而人們對振幅的理解最深。而且光的振幅控制起來也最為容易，一張簡單的半透膜就可以改變光強。對光振幅進行記錄最簡單的辦法就是照相技術，電影就是利用光電器件或膠片對拍攝光場的振幅進行記錄，并將其再現出來。在各個領域都有光振幅的身影。而光的相位與振幅相比，人們對于它的探索還相對較少。究其原因，人們還沒有直接探測光相位的手段，當今人們還只能利用干涉技術通過對干涉條紋的研究，間接地測量相位信息。因此受到光源相干性和器材精度等的限制，相位探測還有較大的發展空間。目前階段，全息技術是光波相位的記錄和再現最有效的手段，為高精度的控制提供了可能[11]。

全息干涉計量可以求解被測區域的振幅和相位分布，具有較高的空間分辨率和時間分辨率。例如在研究物理狀態變化極快的瞬時現象、瞬時過程(如爆炸和燃燒等)時，可以用全息干涉計量的方法對記錄下該過程，再進行研究。而實際使用中干涉條紋會受到振幅、相位及偏振的共同影響。但由于傳統的全息計量對于偏振態分布的求解毫無辦法，也就是只能探究同偏振態的情況。因此發展新的全息干涉計量技術是分別探究振幅、相位和偏振態狀態的前提[12-14]。

偏光全息技術在此背景下應運而生。一旦偏光全息解決了對波面偏振分布的計算問題，那么記錄并再現波面的偏振狀態就成為了可能，甚至可以對其加以控制，擴展傳統全息的應用范圍。偏光全息技術還充實了全息的理論體系，提供了光波偏振態高精度控制、光全息存儲技術擴容以及微納結構偏光器件的高效、低成本制作等研究的理論依據和技術方案[15-17]。

1965年，Lohmann首先提出了用兩束偏振方向相互垂直的參考光來記錄光波的偏振狀態[18]。1968年，Fourney等人從實驗的角度，驗證了Lohmann提出的理論，記錄并再現了光波的偏振狀態[19]。通常把這種全息術稱為偏光全息術, 以示與傳統全息術的區別，其特點就是必須把光波作為矢量波來處理。但當時對偏振的記錄僅僅是矢量分解，依靠兩個分量之間的位相關系再現物光波的偏振態。這也就對實驗條件有較高的要求，實驗的結果和可重復性也有一定的局限。

直到1974年，D.Kakichashvili利用光致各項異性材料實現了對光波偏振態的記錄。之后L.Nikolova和P.S.Ramanujam完善了偏光全息理論。他們引入了瓊斯矩陣，用它可以更簡單地描述偏光全息的記錄和再現過程，但是該理論有較大的局限。其僅在兩束偏振光夾角很小的條件下才能成立[20]。

2011年，東京大學的Kuroda等人依靠三維張量，計算了全息材料曝光前后介電張量的變化，解決了對任意角度下偏光全息的求解問題，提出了全新的偏光全息理論[21]。

2 偏光全息材料介紹

偏光全息材料能夠記錄干涉光場的偏振態分布，是研究偏光全息的基礎。偏光敏感材料具有光致各向異性，當用偏振光去激發材料時，使生成物分子在空間有一定的取向排列，分子的取向方向隨干涉場的偏振態變化而變化。而干涉場的偏振態是由兩束相干光的偏振態共同決定，其變化相對復雜，在此以較為簡單的線偏光為例進行展示。當采用兩束共軸、光強相等、振動方向正交的線偏振光進行干涉，會產生偏振態周期性變化的干涉場，疊加后的偏振態是由兩束光之間的相位差決定的(見圖1)。因此，生成物的分子取向也會出現周期性的變化，那么這種利用偏振態的空間調制，誘導偏光材料的分子取向周期性變化而記錄的光柵為偏光記錄技術。

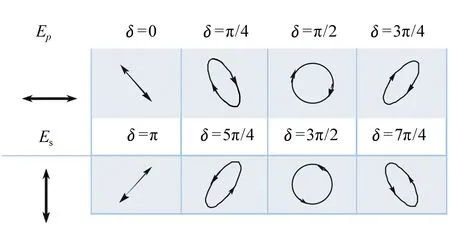
圖1 疊加光場偏振態隨相位差變化圖 Fig.1 Polarization state of interference wave field changes with the variety of phase difference

報道較多的具有各向異性的材料有光折變晶體材料、光致變色材料、光致聚合物材料等幾大類。晶體材料是大家最為熟知的存儲材料，但成本高。光致變色材料主要有偶氮類化合物、二芳基乙烯類[22]、螺噁嗪類[23,24]等。較為常見的方法一般為將其偏光敏感的化合物摻雜在聚合物基質中，或通過化學鍵將其分子連接在聚合物的支鏈上，制備成存儲材料。其中研究較為廣泛的為偶氮類化合物，研究方向主要有主-客摻雜體系，將偶氮類染料摻雜到有機載體聚甲基丙烯酸甲酯[25]或聚乙烯醇[26]中；偶氮主鏈或側鏈[27,28]體系；偶氮聚合物液晶材料體系[29]和偶氮類共聚物[30]等。

光致聚合物是一種感光性高分子材料， 1969年首次被報道，一般的光致聚合物材料具有制造工藝簡單、成本低廉等優勢，同時具備動態范圍大和光敏感度高等優點。由單體、光敏劑和引發劑組成。在光照情況下，光敏劑吸收光子，受激發躍遷到較高的能級，弛豫過程中將能量傳遞給引發劑，使之產生自由基，這些自由基引發小分子或單體發生聚合，生成聚合物。因此光致聚合材料在光照過程中會使材料體積收縮，導致全息圖再現受到影響。

菲醌(PQ)/聚甲基丙烯酸甲酯(PMMA)材料因體積收縮可忽略不計受到研究者的關注，其屬于光致聚合物材料的一種。因材料制備過程將熱致聚合反應和光致聚合反應分開，熱致聚合反應過程中單體聚合成鏈，這時體積發生收縮，形成光透明度好，性能穩定的聚合物基底PMMA；在光照時，材料中單體大部分因已經聚合成鏈，導致體積收縮可忽略不計。PQ在光照的條件下，吸收光子被激發生成單重激發態1PQ*，單重激發態轉變為三重激發態3PQ*，三重激發態的PQ奪取H原子，生成自由基HPQ·與不飽和乙烯基C=C 發生一對一的鏈合反應，生成主要的光產物[31,32]。PQ材料化學名稱為9,10-菲醌，因此具有高共軛，共平面的化學結構，光產物的生成使材料具有各向異性。

結合可忽略體積收縮和具有各向異性這兩種特點，使得PQ/PMMA在厚、體材料的偏光全息領域具有很強的潛力。

PQ/PMMA材料采用熱致聚合法制備，測試材料衍射效率的光路是基于黑田和男教授提出的新偏光全息理論搭建的。

材料的合成步驟為：

(1)依次稱量單體MMA、光敏劑PQ、熱引發劑AIBN，并放入反應瓶中，實驗投料比為MMA∶PQ∶AIBN=10∶0.07∶0.06。

(2)將反應瓶放入60 ℃超聲水浴中超聲，使PQ完全溶解，在磁力攪拌器中60 ℃進行預聚合反應，至小瓶中溶液達到甘油粘性即可停止。

(3)將預聚合后的粘稠的溶液注入硅膠板和玻璃制成的容器內，并將其轉移至烘箱中，60 ℃條件下反應24 h，使材料完全固化。

(4)之后轉移至冰箱冷凍層，使其停止聚合反應，取出后去掉夾子和玻璃外套，得到片狀材料(如圖2)，用鏡頭紙和錫箔紙密封包裝后保存待用。制備的樣品標記為PQ/PMMA，并對材料的厚度進行了考察，確定為1.5 mm厚的材料為最佳。

圖2 PQ/PMMA片狀材料 Fig.2 PQ/PMMA in plate form

因PQ為光敏劑，對材料的影響較大，常溫下PQ在MMA的飽和溶解度為0.7%(質量比)，通過加熱的方法可將PQ的溶解度提高至10%(質量比)[33]，并考察了光敏劑PQ對材料性能的影響。以 0.1%(質量比)為間隔，從 0.7%(質量比)到1.0%(質量比)改變PQ溶解在MMA中的質量比。

圖3中可以看出，溶解在 PQ/PMMA 材料中的 PQ 越多，可以得到高的衍射效率和快的相應速度。但因PQ在單體MMA溶解度的限制，使通過溶解更多光敏劑PQ來獲得較高的衍射效率這一路徑受到了阻礙。今后將在此方向進行深入的研究。

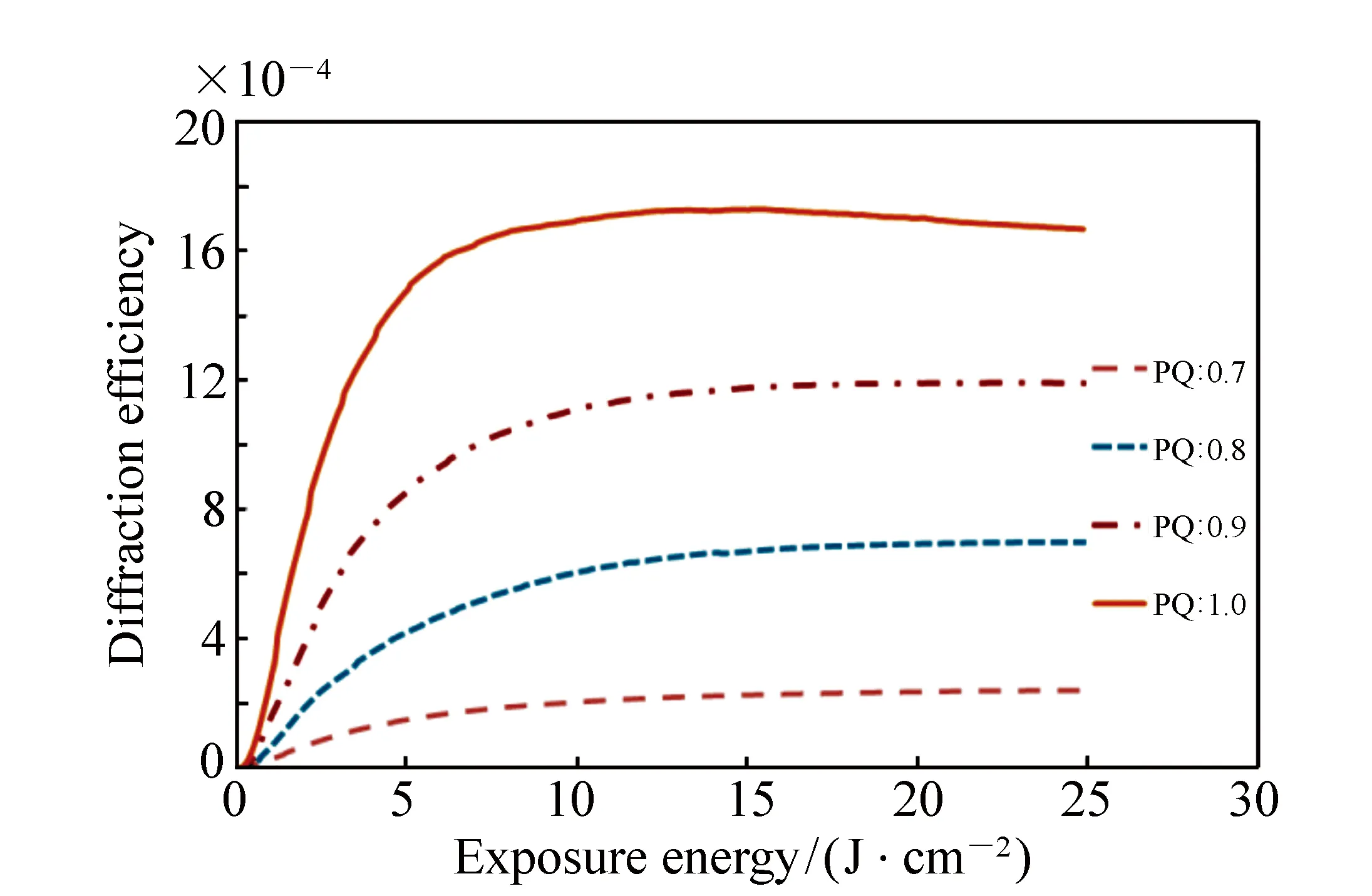
圖3 衍射效率隨PQ濃度變化圖 Fig.3 Variation of diffraction efficiency with PQ′s concentration

3 基于傳統的瓊斯理論的偏光全息理論介紹

自2009年，L.Nikolova和P.S.Ramanujam提出利用瓊斯矩陣計算偏光全息以來，偏光全息的計算求解問題得到了大量的簡化。該理論雖然有較大的限制，但是當滿足傍軸近似的條件時，偏光全息的計算結果會與實際有較好的統一性，并且計算較為簡便[34-35]。

基于瓊斯矩陣的偏光全息計算，簡單來說就是將三維振動的光波電磁矢量在振動面上用瓊斯矩陣描述出來。由于瓊斯矩陣僅能描述二維的振動，因此傍軸近似是瓊斯理論必需滿足的條件。

由干涉光照射光致各向異性材料所引入的雙折射位相差可以表示為:

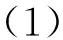
對于吸收率不隨偏振狀態變化而改變的材料，可以定義曝光后材料的折射率為:

式中，n0為材料初始折射率，n//和n⊥分別為垂直和水平方向的光致各向異性折射率。表示為更一般的形式:

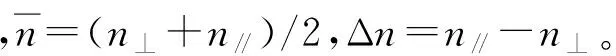
通常材料的水平與垂直折射率變化與光強成正比關系，即可表示為n//=k//I，n⊥=k⊥I。這里k//和k⊥為材料各向異性折射率的比例系數。

對于更一般的入射光為橢偏光的情況，有n//=k//a2+k⊥b2，n⊥=k⊥a2+k//b2。其中a、b分別為橢圓的長短軸。帶入折射率矩陣可得:

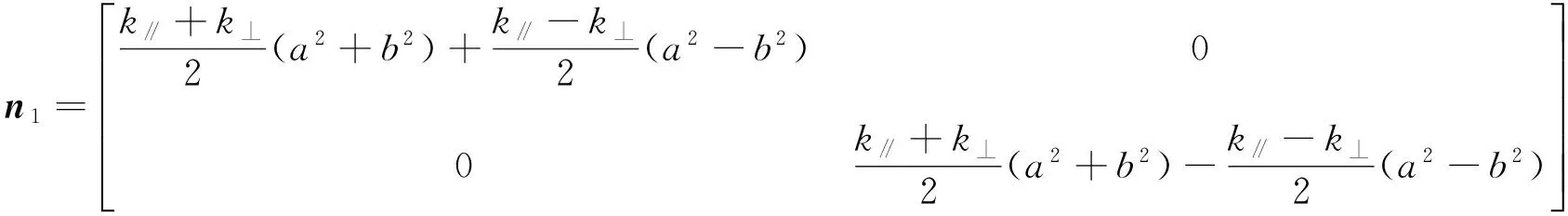
令H=(K//-k⊥)/2,L=(K//-k⊥)/2,則上式可簡化為:

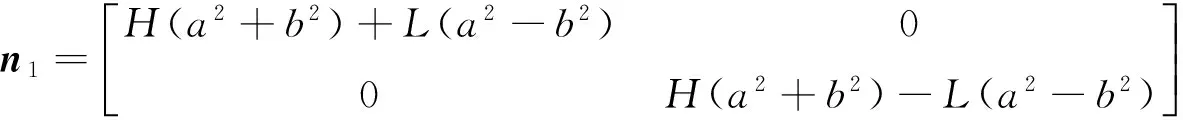
為了得到n1在x0y坐標系下的瓊斯矩陣n1xy，將上式得到的斜橢圓坐標系下的n1做坐標系變換。即將斜橢圓所在坐標系旋轉-Ψ到x0y坐標系，并用入射偏振光的斯托克斯參量進行簡化，得:

式中，S1、S2和S3為斯托克斯參量形式如下:

S0=(a2+b2)

S1=(a2+b2)cos(2Ψ)

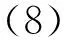
該矩陣就是利用瓊斯矩陣計算得到的光致各向異性材料曝光后的折射率矩陣。在實際的應用情況中通常入射光為線偏振光或圓偏振光，下面將以這兩種光作為實例進行討論[20,36-41]。

3.1入射光為線偏振光時的瓊斯矩陣

當入射信號光和入射參考光的偏振狀態分別為-45°和+45°線偏光時，其可以表示為:

其中G+為入射信號光，G-為入射參考光。δ=2πsinθξ/λ，ξ為水平距離。

再現時用線偏振光照射，其瓊斯矩陣為:

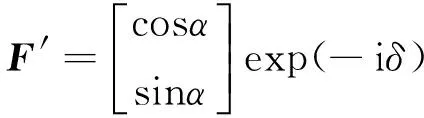
經計算得正負一級衍射光的瓊斯矩陣為:

式中，Δφ=ΔΦ/2=πΔnd。

從該等式中可以看出正負一級衍射光光強相同，偏振態依舊為線偏振光，而偏振方向發生了旋轉。這里全息記錄下的光柵對線偏振光的作用和二分之一波片相同。其他衍射級次可以用相同方法分析得出[42]。

3.2入射光為圓偏振光時的瓊斯矩陣

當入射信號光和入射參考光的偏振狀態分別為右旋和左旋圓偏光時，其可以表示為:

式中，δ=2πsinθξ/λ，ξ為水平距離。

再現時用橢圓偏振光照射，其瓊斯矩陣為:

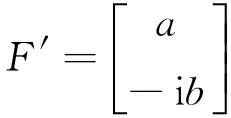
計算后得到正負一級衍射光的瓊斯矩陣為:

從中可以得知正負一級衍射光分別為右旋和左旋圓偏振光。它們的光強為:

如果參數b=a，即再現光為左旋圓偏光時，衍射光將只有+1級一個衍射級次，并且光強正比于sin2(Δφ)。其可以通過選擇合適的Δφ值，例如令Δφ=π/2，這樣+1級的衍射效率在理論上達到100%，同時-1級衍射消失。同理在Δφ=π/2時，用右旋圓偏光作為再現光照射衍射光柵，+1級衍射光將會消失，-1級衍射光的效率將會達到100%[43-44]。

以上獨特的性質使得圓偏光在偏光全息中有著十分廣泛的應用前景。

4 基于張量理論的偏光全息研究進展介紹

如上文所述，L.Nikolova和P.S.Ramanujam使用瓊斯矩陣描述了偏光全息的記錄和再現過程，但由于理論的局限，其僅在傍軸近似的條件下成立[20]。直到2011年，東京大學的Kuroda等人引入了張量概念并提出了全新的偏光全息理論[21]，上述的問題才得到解決。

該偏光全息理論是黑田和男教授利用光致各向異性介質的特性得出的。在外界電磁場的環境中，光致各向異性材料內部分子會發生極化。由于各向異性材料的介電系數不同于各項同性材料，因而使用介電張量表示。再結合體全息中的耦合波理論就得到了該偏光全息張量理論[46-47]。

近幾年，已有一些研究者基于偏光全息張量理論做了研究工作，從最特殊的線偏振光開始，到圓偏振光，到更具有一般性的橢圓偏振光，都有了與理論相符合的實驗結果。未來還可以基于線、圓等偏振理論將其應用到偏振編碼和偏振復用的全息存儲中去[39]。

4.1基于張量理論的偏光全息的記錄、再現過程

在介紹基于偏光全息張量理論的記錄和再現過程之前，先介紹材料中介電張量的變化。如章節二中介紹的，在實際情況當中，有很多種偏振光敏感的材料。該理論以圖4所示的這種桿狀分子為模型，系統地討論了材料曝光前后的介電張量變化，在此忽略了具有旋光性的材料[48-50]。

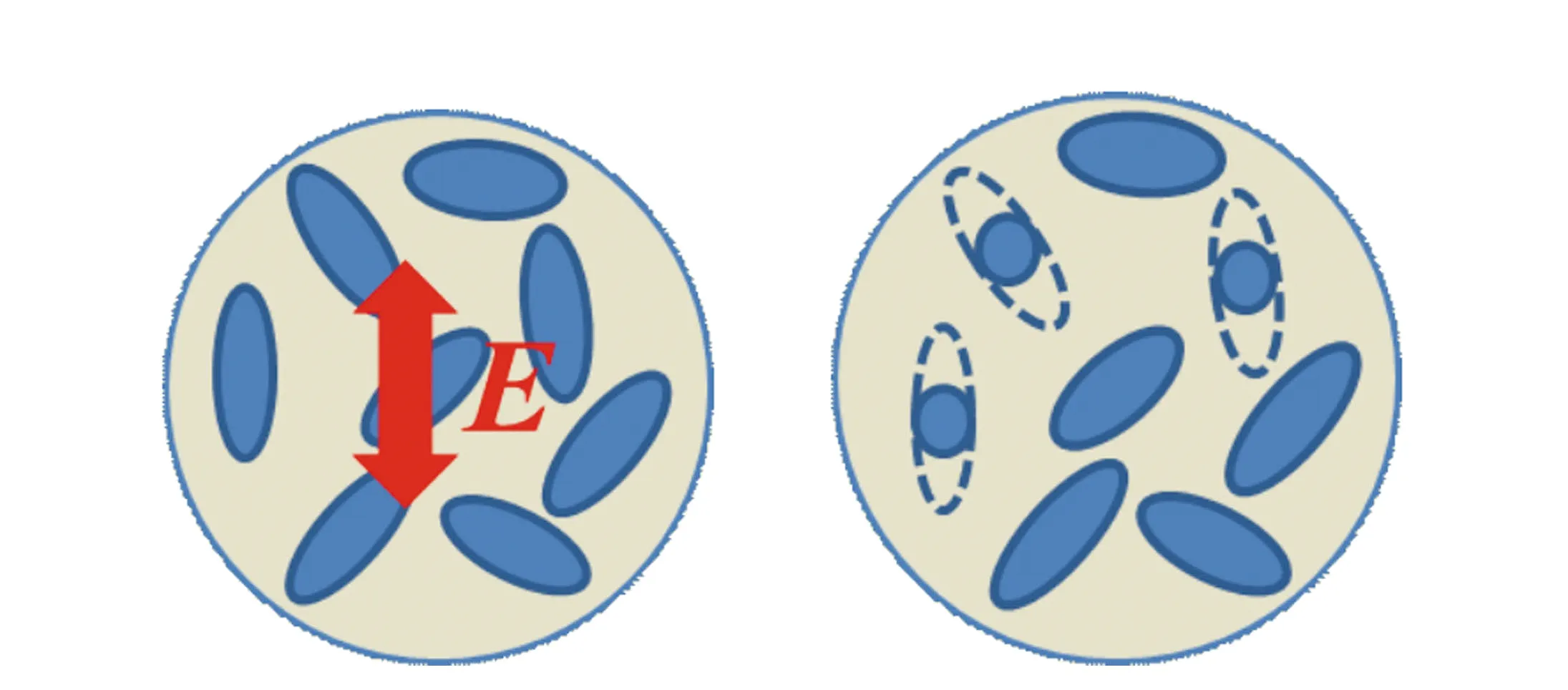
圖4 曝光前后偏光全息材料變化 Fig.4 Variety of polarization holography material before and after exposure

假設具有偏振敏感特性的記錄材料是由具有各向異性極化率的桿狀分子組成的。在曝光前，因為桿狀分子隨機分布在材料中并排列在各個方向，所以材料宏觀上表現出各向同性，其介電系數為常數。通過對光輻射的吸收，也即曝光后，部分桿狀分子被光解為分子碎片。假定由這些分子碎片重新整合而成的分子是各向同性的球狀分子，它們的吸收率取決于極化程度。這樣由于吸收率的偏振敏感特性，使得原來隨機分布的分子的均勻性收到了改變，從而在宏觀上表現出各項異性的性質。此時材料的介電系數應用張量表示，曝光后材料的介電張量的表達式為：

式中，A和B是兩個材料對疊加光場的響應系數。其中A表示材料對光強的響應，即對應則傳統全息的部分。而B表示材料對光場偏振態的響應，是偏光全息所特有的性質。

如圖4所示建立坐標系，xy軸所在平面與材料表面平行，z軸為材料的深度方向。物光波和參考光波分別表示為G+eiq+·γ和G-eiq-·γ，那么干涉形成的光場矢量可以表示為：

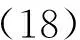
干涉記錄的全息圖的光柵矢量為：

式中，Gj表示光場中的振幅，qj為干涉光波的波矢量，下標“+”和“-”分別表示記錄偏光全息圖所用的信號光波和參考光波。

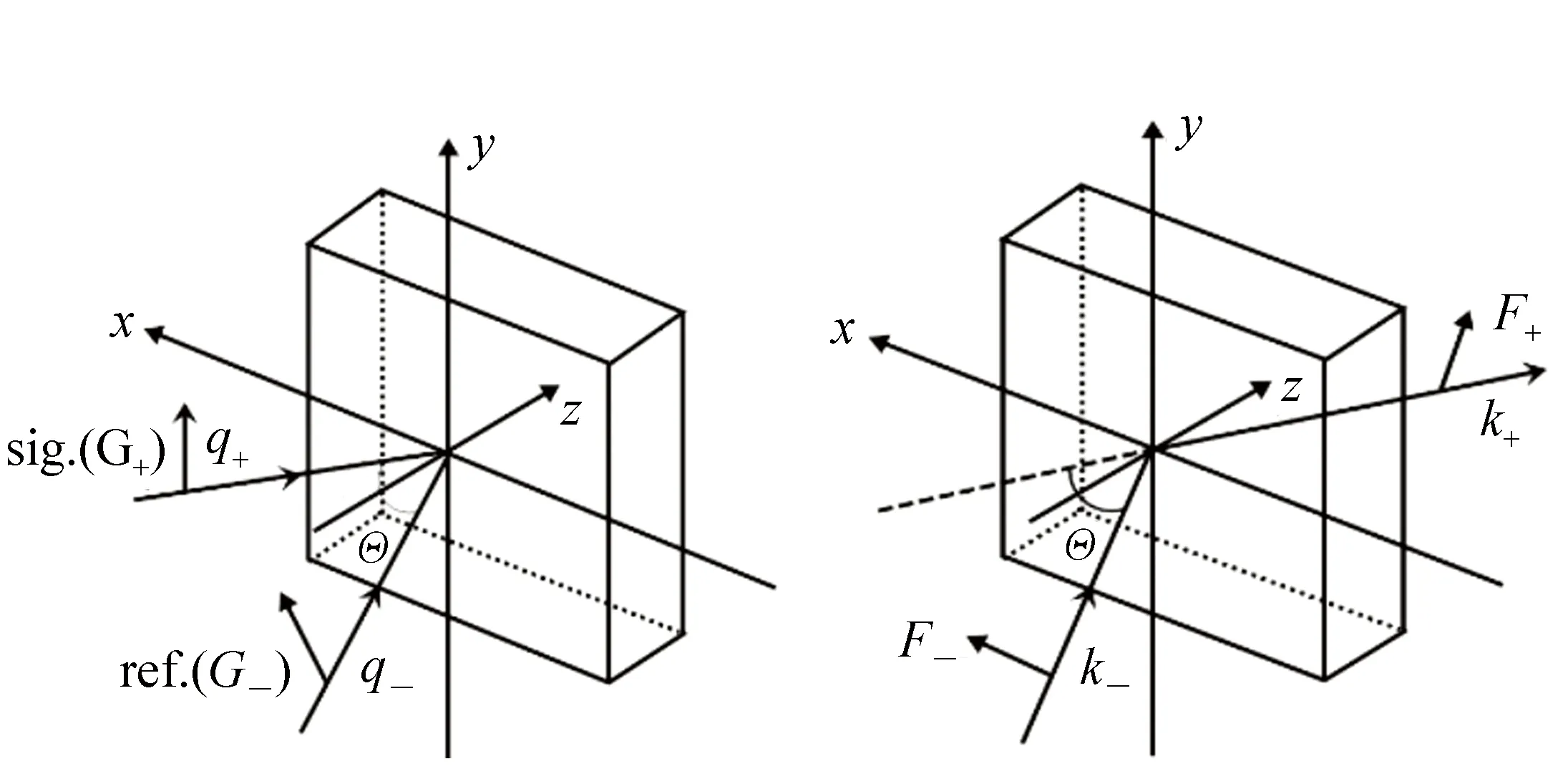
圖5 偏光全息干涉示意圖 Fig.5 Schematic diagram of polarization holography

再現過程中用波矢量為k-的參考光波讀取全息圖(過程如圖5所示)。假設參考光波為F-，再現光波為F+。當嚴格滿足布拉格條件時，可以得到再現光波的波矢量：

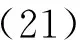
通過麥克斯韋方程組和式(16)，計算后可得再現光波的表達式為：

F+∝X-(X·k+)k+=X++

式中：

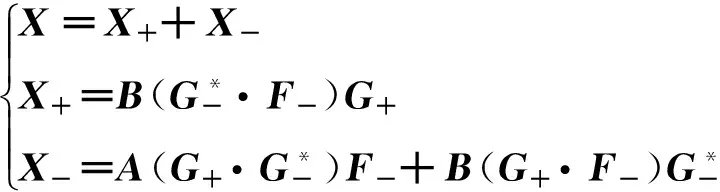
以上所介紹的便是基于介電張量的偏光全息理論。在知道物光波、參考光波和再現參考光波的矢量表達式后，便可以通過該理論求解出衍射光的偏振狀態表達式[51-53]。

4.2基于線偏振光的偏光全息理論研究

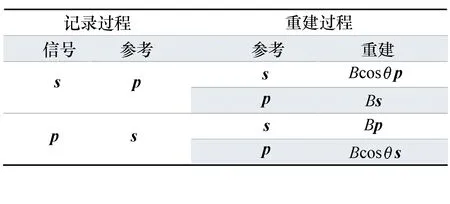
線偏振光作為偏振光中最為基本的一類偏振光，是研究偏光全息理論的基礎。利用上文推導出的再現光波表達式，可以計算得到表1中的結果。其中s表示垂直于入射面的振動方向，p表示平行于入射面的振動方向，θ為信號光和參考光的夾角。

表1線偏光偏光狀態

Tab.1Polarizationstateoflinearpolarizedwave

對于更一般的線偏振光，例如G+=as++bp+，如果令參考光為G-=s-，再現參考光為F-=s-。利用上文提到的再現光波的計算公式(式(22))，可以得到再現光的表達式為：

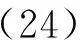
可以看出當滿足“A+B=0”的條件時，再現光波的偏振態就會與物光波的偏振態相同，也就是忠實再現。

圖6(a)為驗證線偏光忠實再現特性的實驗裝置圖，通過P1、P2偏振片和二分之一波片產生實驗所需的線偏振光，并將它們的光強調整為1∶1。用快門控制曝光時間。再現后的衍射光經過PBS偏振分光棱鏡被分為s和p偏振，最后通過功率計測量其強度值。這樣便可以得出再現衍射光的偏振態。

圖6 基于線偏振光的實驗裝置、實驗結果 Fig.6 Experimental setup and experimental result based on linear polarization holography

實驗的結果如圖6(b)所示。在實驗中，隨著曝光量的增加，參量A和B有著不同的變化規律。“A+B=0”這一條件會在某一時刻達到，這時也就是忠實再現物光波偏振態的時刻。人們利用它可以分別實現s、p偏振、45°線偏振等其他角度偏振光的忠實再現。上述的理論計算與實驗很好地從線偏振光的角度證實了基于介電張量的偏光全息理論的正確性[54]。

4.3基于圓偏振光的偏光全息理論研究

圓偏振光是偏振光中一類比較特殊的偏振光，首先，定義左旋圓偏振光和右旋圓偏振光分別為：

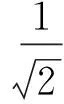
(25)

下面以偏光全息理論為基礎，分4類情況來探究圓偏振下衍射光的特性。理論結果如表2所示。其中分別用l和r代替左旋圓偏振光和右旋圓偏振光。從表2中可以看出，如果再現參考光與記錄參考光的偏振態相同，并且在“A+B=0”的條件下，衍射光也將會有與信號光相同的的偏振態狀態。同樣，在滿足“A+B=0”的情況下，如果再現參考光與原始記錄參考光偏振態正交，則不會有衍射光出現。上述這兩類實驗情況分別稱為圓偏光的忠實再現和零再現。

表2圓偏光偏振狀態

Tab.2Polarizationstateofcircularpolarizedwave

實際實驗的裝置如圖7(a)所示：通過偏振分光棱鏡PBS1將激光分為信號光和參考光。然后通過相應水平方向(P1)與垂直方向(P2)的起偏器以及快軸與水平夾角45°的四分之一玻片(QWP1和QWP2)得到左旋圓偏振光和右旋圓偏振光分別作為信號光和參考光，并在材料上發生干涉生成全息圖。再現時關閉快門2、3，通過轉動QWP2來得到實驗需要的再現參考光的偏振狀態，并照在材料上發生衍射。衍射產生的再現光波通過快軸與水平方向成45°的四分之一玻片QWP3以及偏振分光棱鏡PBS2，將對應的左右旋圓偏振光分別轉化為s和p分量，最后用功率計測出其光強。

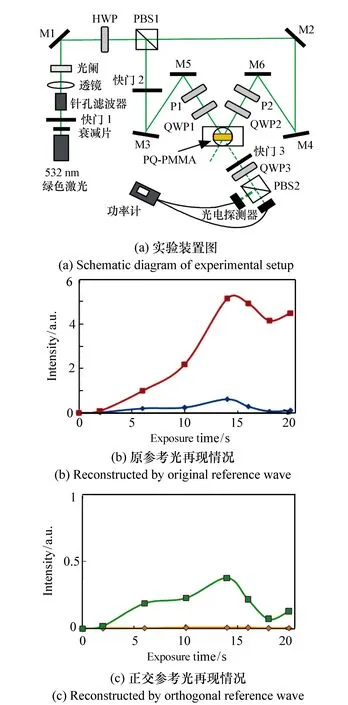
圖7 基于圓偏光實驗裝置、實驗結果 Fig.7 Experimental setup and experimental result based on circular polarization holography

從理論中，可以看出在“A+B=0”的條件下，如果用與記錄參考光偏振態一致的再現參考光便可以忠實再現出信號光，此時測得的右旋偏振光分量應該為0；當再現參考光與記錄參考光偏振態正交時，發生零再現現象，此時測得的左、右旋圓偏振光分量都應該為0。根據不同的曝光時間可以得到以下實驗現象，如圖7(b)、7(c)所示。

隨著曝光量的逐漸增加，測得再現光中左旋圓偏振光分量和右旋圓偏振光分量的強度值是先逐漸增加后減小的，最后在大約18 s的時刻右旋分量變為0，此時左旋分量依然存在，此時也就實現了對信號光的忠實再現[55-57]。

4.4基于橢圓偏振光的偏光全息理論研究

橢圓偏振光與線偏振光、圓偏振光相比，情況更為復雜。為了方便書寫和推導，在這里首先引入了橢圓率的概念。首先，定義橢圓偏振光的矢量表達式為G+=as+±ibp+。

為后續運算的簡化以及統一，在此規定符號e=b/a(e僅表示數學上的換元符號)，其中a、b為偏振橢圓的長短軸。橢圓率e的正負和大小也就分別代表了橢圓偏振光的旋向和形狀。

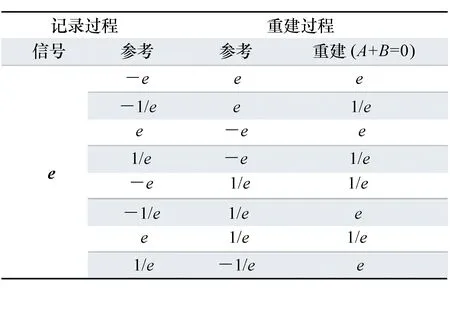
與線偏振光和圓偏振光類似，橢圓中依然存在著忠實再現，并且也是在滿足“A+B=0”的前提條件下實現的。而與前者不同的是，橢圓偏振光的記錄參考光與再現參考光旋向相反時，橢圓偏振態信號光才可以被忠實再現。當記錄參考光與再現參考光正交時，再現光波變成一個與記錄信號光長短軸互換，但是旋向不變的橢圓偏振光。這里將這種現象稱為反轉再現，理論計算結果參見表3中，實驗光路圖見圖8(a)。

表3橢圓偏振光偏振狀態

Tab.3Polarizationstateofellipticalpolarizedwave

光路中通過偏振分光棱鏡PBS1將激光分為信號光和參考光。然后通過各路上的二分之一波片和四分之一波片將線偏光轉化為正橢圓偏振光。再現過程中通過改變參考光路上的二分之一波片來改變橢圓率，以得到需要的偏振態。實驗中用快門2、3來控制實驗進程，并用PBS和兩個功率計探測衍射光的偏振態和光強。由于橢圓率的大小是任意的，本次實驗中將信號光的橢圓率設定為2，即G+=s++i2p+。記錄參考光與信號光旋向相反，形狀相同，即G-=s--i2p-。

首先用F-=2s-+ip-做再現參考光，測得的數據如圖8(b)所示。在圖8(b)當中，橫坐標為曝光時間，縱坐標是功率計所測得的s分量和p分量光強的比值。這個比值隨著曝光時間的增加，先緩慢減小，隨后增大。在曝光時間大約為26 s時，此時光強比約等于4，即此時再現光可以表示為F+=2s++ip+。說明在26 s左右實現了對信號光的反轉再現，此時也應該是“A+B=0”這一點，即偏光全息和強度全息達到了一個平衡。之后還原之前的裝置，立刻旋轉再現光一路的二分之一波片，將再現參考光改為F-=s-+i2p-，再次照射全息圖。此時再現參考光與記錄參考光偏振態相同，旋向相反。得到的結果如圖8(c)所示，s分量和p分量的光強比幾乎不隨著時間改變，保持在0.25左右，也就是此時實現了忠實再現。這也進一步證明了此時的A+B=0[58-61]。

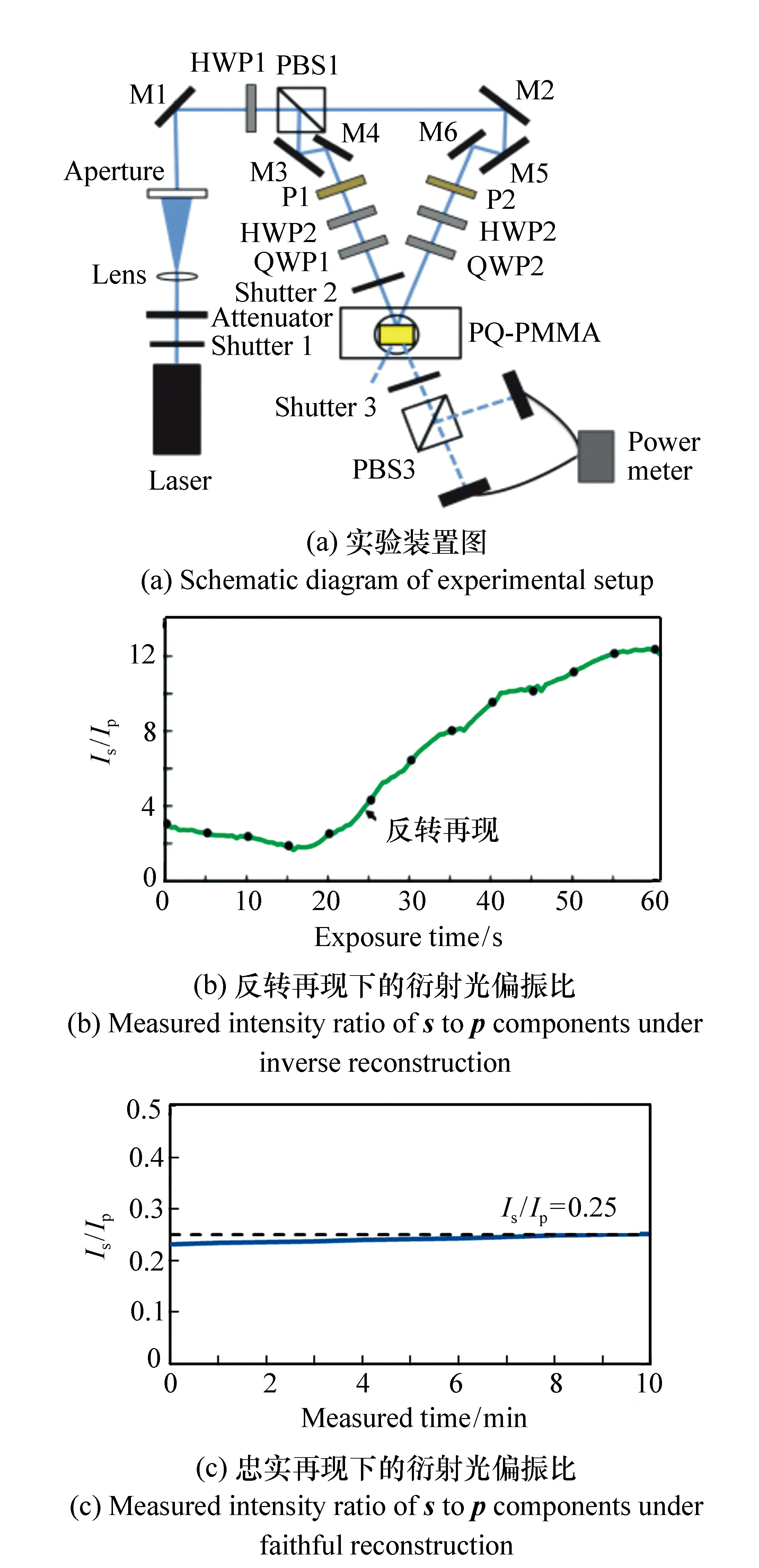
圖8 基于橢圓偏光的實驗裝置、實驗結果 Fig.8 Experimental setup and experimental result based on ellipse polarization holography

偏光全息和強度全息達到平衡，本來是一個很抽象的概念。這里通過先假設反轉再現成立，此時“A+B=0”。再改變再現參考光偏振態，使其成為一個與記錄參考光旋向相反、形狀相同的橢圓偏振光，用它去照射全息圖。若此時忠實再現成立，那么前后實驗結果相互驗證，也就證實了此時偏光全息與強度全息達到了平衡[62-63]。

以上論述，無論是線偏振光的忠實再現，還是圓偏振光的忠實再現、零再現，橢圓偏振光的忠實再現、反轉再現，都從實驗中驗證了基于張量理論的偏光全息理論的正確性[64-66]。

5 偏光全息的主要應用和下一步展望

偏光全息主要可以應用到以下兩個方面。首先全息存儲作為未來大數據存儲的一個有力競爭者，還有著很大的發展空間。傳統的全息存儲主要是對振幅和位相進行編碼，而沒有考慮偏振狀態。這時如果在原有的基礎上將偏振作為一個新的維度添加到全息存儲中，將會極大地提高全息存儲的存儲密度[67-70]。

當今是一個大數據的時代，每時每刻都有海量的數據被制造出來。而如何高效地保存這些數據是一個現階段急需解決的問題。根據美國的國際數據公司IDC統計，僅2010年一年內全世界就生產了1ZB的數據量，并估計到2020年這一數字將會增長到40ZB的規模。因此，依托這樣的一個前景，大數據存儲將有一個廣闊的市場前景，其產值必將逐年增加[71-74]。

目前數據存儲的有效手段包括磁存儲，半導體存儲以及光存儲。其中磁存儲受材料及環境等因素的影響，退磁是一個不得不考慮的問題，因而對于長時間大數據的存儲并不是一個完美的解決方案。而半導體存儲由于其制作其成本較高因而也不能很好的解決該問題。據光存儲的老化加速實驗表明，其保存時長可達50年[75]。并且其僅在存儲與讀取時有能量消耗，非常適合大數據的長時間存儲[76-77]。

與傳統光盤相比，光全息存儲是將三維光柵存儲在全息材料中，再以二維的形式按數據頁讀取傳輸出來，因此有著無可比擬的讀取速度和存儲容量，使其成為高密度存儲最有力的競爭者之一[78-80]。在20世紀60年代激光的發明以來，用全息技術作為數據的存儲方式就已經被人們所研究。但是受到材料分辨率與噪聲等因素的影響，其存儲密度與理論極限還有較大的差距。因此將偏振態作為新的調制參量增加到其中，從而為提高數據密度的提供了一個有效的發展方向[81-82]。

除了應用在光全息存儲方面，偏光全息技術還能應用在光學元件制作中。由于在偏光全息中，通過控制信號光和參考光的偏振態就可以實現對衍射光波的偏振態進行控制。因此，利用這一特性可以方便地制備納米光學元件[83]。

納米光學領域，矢量計算理論，如傅里葉模態法、有限時域差分法、有限元法、邊界元法等受益于計算機技術得到的飛速地發展。然而與之相對應的是納米光子器件的制作方法，包括微納制作工藝，包括真空鍍膜、電子束直寫、反應離子束刻蝕等技術，還處于相對落后的階段[84-85]。用上述方法制作的器件的微觀特征尺寸在100 nm左右，宏觀特征尺寸約為1×1 mm，無法大面積制造。并且其適用波長還受到限制，深紫外、極紫外等短波段的亞波長納米偏振器件的制作還是一個難題。偏光全息作為一種干涉記錄手段，選擇合適的光源和材料就可以在任意波段制作偏光器件。此外，對光束口徑的控制較為容易，因而可以方便地用其制作大面積的偏振光學元件。如果與大口徑的空間透鏡配合，還以將其用于空間偏振成像探測。

綜上所述，偏光全息技術有著較為廣闊的應用前景，但是，從中也可以看出其使用前提是找到穩定、高效的偏光全息材料。因此，在偏光全息理論發展的同時，偏光全息材料也需要得到人們的重視。理論與材料共同發展，才能更好地將偏光全息技術應用于實際生活當中。

6 結 論

傳統的全息術可以記錄光振幅和相位信息，偏光全息在傳統全息術的基礎上增加了對光波偏振態的記錄。其發展大體經歷了兩個階段，分別是瓊斯理論階段和張量理論階段。它們之間的最大區別在于干涉角度的大小：即傳統的瓊斯理論是在傍軸近似的前提下成立的，而張量理論可以擴展到任意角度。

在應用方面，光的偏振狀態可以成為全息光存儲中的一維調制參量，從而使其在原有的基礎上提高記錄密度，是未來一個可能的發展方向。其次，偏光全息技術還可以作為傳統微納工藝的補充手段，用于大面積、短波長的納米光學元件制作，擴展納米元件的使用范圍。

[1] GABOR D. A new microscopic principle[J].Nature,1948,161:777-779.

[2] LEITH E N,UPATNIEKS J. Reconstructed Wavefronts and Communication Theory[J].J.OpticalSocietyofAmerica,1962,52(10):1123-1130.

[3] DENISYUK YU N. Photographic reconstruction of the optical properties of an object its own scatteredradiation field[J].SovPhys-Dokl,1962,7:544-546.

[4] VANDER LUGT A,ROTZ F B,KLOOSTER A. Character reading by optical spatial filtering[M]//OpticalandElectro-OpticalInformationProcessing. New York:Mass Inst Technology Press,1965:125-135.

[5] BENTON S A. Hologram reconstructions with extended light sources[J].J.OpticalSocietyofAmerica,1969,59(10):1545- 1547.

[6] WHITE J G,AMOSW B.Confocal microscopy comes of age[J].Nature,1987,328:184-184.

[7] SON J,JAVIDI B,KWACK K. Methods for displaying three-dimensional images[J].ProceedingsoftheIEEE,2006,94(3): 502-523.

[8] OSTROVSKY Y I,BUTUSOV M M,OSTROVSKAYA G V.InterferometrybyHolography[M]. Berlin:Springer,1980:184-191.

[9] Y Z L,JIN G F.Computer-generatedHologram[M]. Beijing:Tinghua University Press,1984:12-30,48-50.

[10] CURTIS K,DHAR L,FACKE T. Holographic data storage:coming of age[J].NaturePhoton,2008,2(7):404-405.

[11] 吳安安.基于圓偏振光的偏光全息理論基礎研究[D].北京:北京理工大學,2015.

WU A A. Polarization holography based on the circular polarized wave[D]. Beijing:Beijing Institute of Technology.,2015.(in Chinese)

[12] KIHARA T,KUBO H,NAGATA R. Isopachics measurement using immersion method polarization holography[J].AppliedOptics,1976,15(12):3025-3028.

[13] 趙娟.激光技術在醫學上的應用[J].醫療衛生裝備,2003,24(7):18-19.

ZHAO J. Application of laser technology to medicine[J].ChineseMedicalEquipmentJournal,2003,24(7):18-19.(in Chinese)

[14] 謝敬輝,孫萍.全息術的新進展[J].北京理工大學學報,2003,23(2):136-138.

XIE J H,SUN P. New Advances in Holography[J].J.BeijingInstituteofTechnology(Natural Science Edition),2003,23(2):136-138.(in Chinese)

[15] CURTIS K,DHAR L,HILL A,etal..HolographicDataStorage:FromTheorytoPracticalSystems[M]. New York:John Wiley & Sons Ltd,2010:1-14.

[16] COUFAL H J,PSALTIS D,SINCERBOX G T.HolographicDataStorage[M]. Berlin:Springer-Verlag,2000:1-17.

[17] HEANUE J F,BASHAW M C,DAIBER A J,etal.. Digital holographic storage system incorporating thermal fixing in lithium niobate[J].OpticsLetters,1996,21(19):1615-1617.

[18] LOHMANN A W. Reconstruction of vectorial wavefronts[J].AppliedOptics,1965,4(12):1667-1668.

[19] FOURNEY M E,WAGGONER A P,MATE K V. Recording polarization effects via holography[J].J.OpticalSocietyofAmerica,1968,58(5).

[20] NIKOLOVA L,RAMANUJAM P S.PolarizationHolography[M]. Cambridge:Cambridge University Press,2009:25-85.

[21] KURODA K,MATSUHASHI Y,FUJIMURA R,etal.. Theory of polarization holography[J].OpticalReview,2011,18(5):374-382.

[22] PU S,YANG T,YAO B,etal.. Photochromic diarylethene for polarization holographic optical recording[J].MaterialsLetters,2007,61(3):855-859.

[23] FU,S,LIU Y,DONG L,etal.. Photo-dynamics of polarization holographic recording in spirooxazine-doped polymer films[J].MaterialsLetters,2005,59(11):1449-1452.

[24] FU S,LIU Y,LU Z,etal.. Photo-induced birefringence and polarization holography in polymer films containing spirooxazine compounds pre-irradiated by UV light[J].OpticsCommunications,2004,242(1-3):115-122.

[25] VINHPHUC P G M,ROGER A L,RICCARDO P. Real-time dynamic polarization holographic recording on auto-erasable azo-dye doped PMMA storage media[J].OpticalMaterials,1995,4:467-475.

[26] COUTURE J J. Polarization holographic characterization of organic azo dyes/PVA films for real time applications[J].AppliedOptics,1991,30(20):2858.

[27] KAWATSUKI N,MATSUSHITA H,KONDO M,etal.. Photoinduced reorientation and polarization holography in a new photopolymer with 4-methoxy-N-benzylideneaniline side groups[J].Appl.Materials,2013,1(2):37.

[28] CIPPARRONE G,PAGLIUSI P,PROVENZANO C,etal.. Polarization holographic recording in amorphous polymer with photoinduced linear and circular birefringence[J].J.PhysicalChemistryB,2010,114(27):8900.

[29] MAO W,SUN Q,BAIG S,etal.. Red light holographic recording and readout on an azobenzene-LC polymer hybrid composite system[J].OpticsCommunications,2015,355:256-260.

[30] ZHAO F,WANG C,QIN M,etal.. Polarization holographic gratings in an azobenzene copolymer with linear and circular photoinduced birefringence[J].OpticsCommunications,2015,338:461-466.

[31] CHEN P L. Phenanthrenequinone-doped copolymers for holographic data storage[J].OpticalEngineering,2009,48(3):035802(1-6).

[32] STECKMAN G J. Holographic recording in a photopolymer by optically induced detachment of chromophores[J].OpticsLetters,2000,25(9):607-609.

[33] HONGPENG L,D Y,XUECONG L,SUHUA L,et al.. Diffusional enhancement of volume gratings as an optimized strategy for holographic memory in PQ-PMMA photopolymer[J].OpticsExpress,2010,18(7):6447-6454.

[34] NIKOLOVA L,MARKOVSKY P,TOMOVA N,etal.. Optically-controlled photo-induced birefringence in photo-anisotropic materials[J].J.ModernOptics,1988,35(11):1789-1799.

[35] TODOROV T,NIKOLOVA L,TOMOVA N,etal.. Photoinduced anisotropy in rigid dye solutions for transient polarization holography[J].IEEEJ.QuantumElectronics,1986,22(8):1262-1267.

[36] TODOROV T,NIKOLOVA L,TOMOVA N. Polarization holography. 1:a new high-efficiency organic material with reversible photoinduced birefringence[J].AppliedOptics,1984,23(23):4309-12.

[37] TODOROV T,NIKOLOVA L,TOMOVA N. Polarization holography.2:polarization holographic gratings in photoanisotropic materials with and without intrinsic birefringence[J].AppliedOptics,1984,23:4588.

[38] TODOROV T,NIKOLOVA L,STOYANOVA K,etal.. Polarization holography.3:Some applications of polarization holographic recording[J].AppliedOptics,1985,24:785.

[39] NIKOLOVA L,TODOROV T,IVANOV M,etal.. Polarization holographic gratings in side-chain azobenzene polyesters with linear and circular photoanisotropy[J].AppliedOptics,1996,35:3835-3840.

[40] NIKOLOVA L,TODOROV T,IVANOV M,etal.. Photoinduced circular anisotropy in side-chain azobenzene polyesters[J].OpticalMaterials,1997,8(4):255-258.

[41] NIKOLOVA L,TODOROV T. Diffraction efficiency and selectivity of polarization holographic recording[J].J.ModernOptics,1984(5):579-588.

[42] WANG C,LI H,WANG J,etal.. Polarization conversions of diffractive wave plates based on orthogonal circular-polarization holography[J].ChineseOpticsLetters,2016,14(1):36-39.

[43] GLEESON M R. Improvement of the spatial frequency response of photopolymer materials by modifying polymer chain length[J].J.OpticalSocietyofAmericaB,2008,25(3):396-406.

[44] LIU S,GLEESON M R,SHERIDAN J T. Analysis of the photoabsorptive behavior of two different photosensitizers in a photopolymer material[J].J.OpticalSocietyofAmericaB,2009,26(3):528-536.

[45] KOSTUK R K. Dynamic hologram recording characteristics in DuPont photopolymers[J].AppliedOptics,1999,38(8):1357-63.

[46] GARCIA C,FIMIA A,PASCUAL I. Holographic behavior of a photopolymer at high thicknesses and high monomer concentrations: mechanism of photopolymerization[J].AppliedPhysicsB,2001,72(3):311-316.

[47] GALLEGO S,ORTU O M,NEIPP C,etal.. 3 Dimensional analysis of holographic photopolymers based memories[J].OpticsExpress,2005,13(9):3543-57.

[48] YAMASAKI K,JUODKAZIS S,WATANABE M,etal.. Recording by microexplosion and two-photon reading of three-dimensional optical memory in polymethylmethacrylate films[J].AppliedPhysicsLetters,2000,76(8):1000-1002.

[49] DAY D,GU M. Formation of voids in a doped polymethylmethacrylate polymer[J].AppliedPhysicsLetters,2002,80(13):2404-2406.

[50] VENIAMINOV A V,BARTSCH E,POPOV A P. Postexposure evolution of aphotoinduced grating in a polymer material with phenanthrenequinone[J].OpticsandSpectroscopy,2005,99(5):744-750.

[51] VENIAMINOV A V,SILLESCU H. Forced Rayleigh scattering from non-harmonic gratings applied to complex diffusion processes in glass-forming liquids[J].ChemicalPhysicsLetters,1999,303(5-6):499-504.

[52] LIU Y,LI Z,ZANG J,etal.. The optical polarization properties of phenanthrenequinone-doped poly(methyl methacrylate) photopolymer materials for volume holographic storage[J].OpticalReview,2015,22(5):837-840.

[53] PAN X,XIAO S,WANG C,etal.. Photoinduced anisotropy in an azo-containing ionic liquid-crystalline polymer[J].OpticsCommunications,2009,282(5):763-768.

[54] ZANG J,WU A,LIU Y,etal.. Characteristics of volume polarization holography with linear polarization light[J].OpticalReview,2015,22(5):829-831.

[55] WANG J,KANG G,WU A,etal.. Investigation of the extraordinary null reconstruction phenomenon in polarization volume hologram[J].OpticsExpress,2016,24(2):1641.

[56] WU A,KANG G,ZANG J,etal.. Null reconstruction of orthogonal circular polarization hologram with large recording angle[J].OpticsExpress,2015,23(7):8880-8887.

[57] LIU Y,ZANGJ L,WU A A,etal.. The optical properties study of PQ/PMMA photopolymer in volume holographic storage[C]. The 11th Conference on Lasers and Electro-Optics Pacific Rim,(CLEO-PR2015),2015,Korea.

[58] ZHANG Y,KANG G,ZANG J,etal.. Inverse polarizing effect of an elliptical-polarization recorded hologram at a large cross angle[J].OpticsLetters,2016,41(17):4126-4129.

[59] 陳運達,汪之國,江奇淵,等.非理想1/4波片對泵浦光偏振態的影響[J].中國光學,2017,10(2):226-233.

CHEN Y D,WANG ZH G,JIANG Q Y,etal.. Influence of nonideal 1/4 wave plate on pump light polarization[J].ChineseOptics,2017,10(2):226-233.(in Chinese)

[60] ZHANG Y Y,ZANG J L,WANG J,etal.. Tsutomu shimura and kazuo kuroda, reconstruction characeristics of polarization holography using the elliptical polarized wave[J].SPIEPhotonicsEurope,2016,9889-24.

[61] 張伊盈，臧金亮，劉穎，等.基于橢偏振光的偏振全息理論基礎研究[C].中國光學學會全息與光信息處理專委會學術年會，上海，中國,2016.

[62] ZHANG Y Y,WU A A,ZANGJ L,etal.. Reconstruction characteristics of elliptical-polarization holography at a large recording angle[C]. International Symposium on Optical Memory 2016(IOSM16)，Kyoto，Japan，2016：We-L-7.

[63] ZHANG Y Y,WU A A,ZANG J L,etal.. Polarization holography written by elliptically polarized wave at a large cross angle[J].SPIEPhotonicsAsia,2016,10022-31.

[64] VINETSKII V L,KUKHTAREV N V,ODULOV S G,etal.. Dynamic self-diffraction of coherent light beams[J].SovietPhysicsUspekhi,1979,22(9):742-756.

[65] HEATON J M,MILLS P A,PAIGE E G S,etal.. Diffraction efficiency and angular selectivity of volume phase holograms recorded in photorefractive materials[J].J.ModernOptics,1984(8):885-901.

[66] SHATALIN I D. Mechanism of photoanisotropy in photochemical trans-cis isomerization[J].Optics&Spectroscopy,1989,66:209-211.

[67] PAN X,WANG C,WANG C,etal.. Image storage based on circular-polarization holography in an azobenzene side-chain liquid-crystalline polymer[J].AppliedOptics,2008,47(1):93-8.

[68] OSTROVERKHOVA O,MOERNER W E. Organic photorefractives:mechanisms, materials, and applications[J].ChemicalReviews,2004,104(7):3267.

[69] KAKICHASHVILI S D,KAKICHASHVILI S D. Polarization-holographic recording in the general case of a reaction of a photoanisotropic medium[J].SovietJ.QuantumElectronics,1983,13(10):1976-1981.

[70] KAKICHASHVILI S D. Regularity in photoanisotropic phenomena[J].Optics&Spectroscopy,1982,52:191-194.

[71] HALL T J,JAURA R,CONNORS L M,etal.. The photorefractive effect-a review[J].ProgressinQuantumElectronics,1985,10(2):77-146.

[72] KOGELNIK H. Coupled wave theory for thick hologram gratings[J].TheBellSystemTechnicalJournal,1969,48(9): 2909-2947.

[73] HUANG T,WAGNER K H. Coupled-mode analysis of dynamic polarization volume holograms[J].SPIE,1991,1559:372-390.

[74] HUANG T,WAGNER K H. Photoanisotropic incoherent-to-coherent conversion using five-wave mixing[J].SPIE,1991,1562:44-54.

[75] 陶世荃.高密度光學全息存儲技術的新進展:向光盤存儲挑戰[J].物理,1997,2:79-85.

[76] DHAR L,CURTIS K,HALE A,etal.. High Density Holographic Data Storage[C]. Optical Data Storage,2000. Conference Digest. IEEE,2000:158-160.

[77] SHI X,LAWRENCE B,ERBEN C. Dye-doped thermoplastics for holographic data storage[J].SPIE,2006,6335:633509.

[78] KELLY J V,GLEESON M R,CLOSE C E,etal.. Temporal response and first order volume changes during grating formation in photopolymers[J].J.AppliedPhysics,2006,99(11):28-160.

[79] ORLOV S S,PHILLIPS W,BJORNSON E,etal.. High-transfer-rate high-capacity holographic disk data-storage system[J].AppliedOptics,2004,43(25):4902.

[80] WAN Y,TAO S,ZHUO D,etal.. Coherent scattering noise properties of a blue laser sensitized holographic photopolymer material[J].SPIE,2007,6827:682711.

[81] NOBUKAWA T,NOMURA T. Multilevel recording of complex amplitude data pages in a holographic data storage system using digital holography[J].OpticsExpress,2016,24(18):21001.

[82] NOBUKAWA T,FUKUDA T,BARADA D,etal.. Coaxial polarization holographic data recording on a polarization-sensitive medium[J].OpticsLetters,2016,41(21):4919.

[83] SRIKHIRIN T,CIMROVA V,SCHIEWE B,etal.. An investigation of the photoinduced changes of absorption of high-performance photoaddressable polymers[J].Chem.Phys.Chem.,2002,3(4):335-342.

[84] 劉全,吳建宏,郭培亮.用于強激光系統的光柵偏振器[J].光學 精密工程,2016,24(12):2962-2968.

LIU Q,WU J H,GUO P L. Grating polarizers for high power laser systems[J].Opt.PrecisionEng.,2016,24(12):2962-2968.(in Chinese)

[85] 程柏,韓冰,谷立山,等.納結構的連續激光復合微納探針刻劃加工[J].光學 精密工程,2015,23(7):2043-2050.

CHENG B,HAN B,GU L SH,etal.. Nanostructure machining by AFM probe combined with continuous laser[J].Opt.PrecisionEng.,2015,23(7):2043-2050.(in Chinese)

Reviewandprospectofpolarizationholography

HONG Yi-fan1, ZANG Jin-liang1, LIU Ying1, FAN Feng-lan1, WU An-an2, SHAO Long1, KANG Guo-guo1*, TAN Xiao-di1

(1.InformationOpticsLaboratory,SchoolofOptoelectronics,BeijingInstituteofTechnology,Beijing100081,China； 2.InstituteofIndustrialScience,UniversityofTokyo,Tokyo153-8505,Japan)

Holography is a very promising technique which records rich information on small holograms by interfering with signal light and reference light. Unlike conventional holography, polarized holography not only records the phase and amplitude information of light waves, but also records additional polarization information in polarized state sensitive materials. In this paper, the production process of polarized holography is introduced in detail based on polarized holographic materials. At the same time, the principle and research progress of polarization holography based on Jones theory and tensor theory are introduced respectively. Finally, the development prospect of polarized holography in holographic storage and nanometer optics is described. In addition, the principle and research progress of polarization holography based on Jones matrix and tensor theory are introduced respectively. Finally, the development prospect of polarized holography in holographic storage and nanometer optics is discussed.

polarization holography;Jones theory;tensor theory;polarization states

TP394.1； TH691.9

A

10.3788/CO.20171005.0588

洪一凡 (1992—)，男，遼寧沈陽人，碩士研究生，2015年于北京理工大學獲得學士學位，主要從事偏光全息光學方面的研究。E-mail：2120150516@bit.edu.cn

康果果(1980—)，男，四川成都人，博士，副教授，博士生導師，主要從事微納光學、偏光全息方面的研究。E-mail:kgg@bit.edu.cn

2017-04-27；

2017-05-25

國家自然科學基金項目(No.61475019, No.61675020)

Supported by National Natural Science Foundation of China(No.61475019, No.61675020)

2095-1531(2017)05-0588-15

*Correspondingauthor,E-mail:kgg@bit.edu.cn