初中數學教學中分析學生認知的三個維度

練兆明

(江蘇省蘇州高新區實驗初級中學，江蘇 蘇州 215000)

初中數學教學中分析學生認知的三個維度

練兆明

(江蘇省蘇州高新區實驗初級中學，江蘇 蘇州 215000)

促進學生認知能力的發展，是中小學階段的重要教學任務之一。具備良好的認知能力，不僅可以促進學生思維健全和智力的發展，也有利于提高學生的學習水平。所以，在初中數學教學階段，更要對培養學生的認知能力形成足夠的重視。本文主要對培養學生認知能力的三個維度進行分析，從而為初中數學開展教學活動奠基。

初中數學；認知能力；角度

對于學生認知分析三個維度，主要指的是認知基礎、認知規律和認知需求，站在這三個角度上的對學生認知能力進行分析，全面了解學生的認知能力發展狀況，在開展課堂教學活動時，有針對性地讓教師教與學生學的節奏一致起來，就可以為打造高效數學課堂奠定堅實的基礎.

一、了解學生的認知基礎

初中數學教學過程中將培養學生的認知能力作為重要教學目標之一，對初中生認知進行著重分析，必須認識到了解學生的認知基礎具有非常重要的作用.主要是因為全面了解學生的認知基礎，分析學生的學習水平和能力，在進行教學設計的時候，以此作為理論依據確保教學設計的有效性和科學性，就可以為開展高效數學課堂教學活動奠定堅實的基礎，從而逐步實現初中數學教學目標.

例如在教學初中數學“平面直角坐標系”這一部分內容之前，教師先展開大范圍調查活動，全面了解學生的學習水平，以期通過調查結果對學生進行認知分析.其中某個學生在調查測試中表現出了空間想象和立體思維發展方面的問題，針對這個問題，教師對學生進行認知分析，可以發現學生的認知尚未發展健全.由此，在開展數學課堂教學活動中，教師有針對性和目的性地將重點集中在拓展學生思維上，通過組織學生對教學內容的深入剖析，使得學生對教學內容形成了深刻的認識.在此基礎上，再次了解學學生的認知能力發展情況，教師提出了與教學內容息息相關的數學問題，如下所示：

例題1：在平面直角坐標系中，點O為原點，點A的坐標為(-6，0)．如圖1，正方形OBCD的頂點B在x軸的負半軸上,點C在第二象限．現將正方形OBCD繞點O順時針旋轉角α得到正方形OEFG．

求：如圖2，若α=60°,OE=OA，求直線EF的函數表達式.

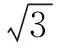
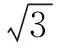
學生順利解出數學問題，不僅只是為了得出正確的結果和結論，重點在于學生探究答案的過程.在這個過程中，學生思維得到升華，大腦在不停‘轉動’，從提出觀點到自我否定，在不斷的自我肯定中逐漸理清解題思路，實則就是學生認知能力發展的重要基礎和前提.

二、了解學生的認知需求

了解學生的認知需求，不僅是對學生認知分析的重要內容，也是數學教學的根本目標.主要是因為學生作為學習的主體，滿足學生的學習需求是教學的基本.所以，在初中數學教學中對學生進行認知的分析，還需要注重對學生進行認知需求的分析，滿足學生的認知需求，提供學生整體學習水平.

三、了解學生的認知規律

學生在學習過程中，掌握一定的規律，對于他們學習也會有很大的幫助.實際上，學生在學習過程中本身就存在一定的規律，且每個學生的規律都可能不一樣.而教師的任務就是發掘學生的規律，找出其中的共性與差異，將其進行有效整合，找到規律與教學目標之間的契合點，從而確保教學活動有效展開.所以，在初中數學課堂教學中，教師深入了解學生的認知規律也是非常重要的.

[1]陳偉.加強思維訓練,提升思考效果——初中數學有效性思維模式探究[J]. 華夏教師,2016(11).

[2]張靜.談初中數學如何培養學生的創新思維[J].中國校外教育,2016(34).

[3] 鄒豐民. 淺談如何打好初中數學學習基礎[J]. 中國校外教育,2015(31).

G632

A

1008-0333(2017)23-0047-02

2017-06-01

練兆明(1981.4-)，男，江蘇省蘇州高新區實驗初級中學，中學一級教師，大學本科，從事初中數學教育.

[責任編輯李克柏]