在中學排課問題中實用的模擬退火算法應用①

唐 環,高 健

(上海大學 機電工程與自動化學院,上海 200072)

在中學排課問題中實用的模擬退火算法應用①

唐 環,高 健

(上海大學 機電工程與自動化學院,上海 200072)

針對中學排課問題,提出了一種分階段的模擬退火算法解決方案.中學排課問題難點主要在于如何解決課表中存在的大量沖突以及如何優化課表.初始化隨機生成一張帶有沖突的課表,經過算法第一階段,人工干預異化解結構,使課表可行; 算法第二階段引導性的改變課表結構使課表滿足通用的軟約束條件; 算法第三階段采用啟發式隨機鄰域異化操作,變異課表,產生更優解.為了滿足實際生產環境中對課表多元化的需求,在UI界面中提供可以手動調節課表機制.經過實驗發現,改進后的模擬退火算法在解決中學排課問題時收斂速度更快,運行效率更高,并且在迭代次數較少的情況下,也能產生可行解.

模擬退火; 排課問題; 人工智能

學校的排課工作是教學管理任務的重要環節之一,同時也是耗時耗力較多的一項工作.傳統的排課工作大多由經驗豐富的教務人員進行手工編排,這種人工排課會導致排課效率低、效果差.為了優化排課質量、充分提高學生學習效率、推進學校信息化辦公教育,利用計算機實現自動排課已經成為必不可擋的趨勢.

排課問題早在20世紀50年代末,國外學者便對其展開研究.1976年,排課問題被證明是一個NP完全問題[1].這一論證奠定了求解排課問題的理論基礎,學者們不再去刻意追求排課問題的最優解,轉而采用相適應的啟發式算法[2]求得排課問題的較優解.

現階段,解決排課問題的方法主要有基于圖論算法[3]、遺傳算法[4,5]、模擬退火算法[6]、回溯法[7]、蟻群算法[8].然而這些研究主要針對大學課表,中學排課問題有其獨有的特點及難點:

(1)為了保證中學學校的教學計劃,對于學生和教室而言,中學課表一般都處于飽和狀態,容易引起沖突,而大學生課表則相對自由;

(2)中學課表問題中每個班級安排的年級課程固定,而在大學課堂上各個教室可以分配不完全相同的教學任務,甚至可以混合多個年級的課程,因此中學教室的靈活性差;

(3)中學對課表質量要求較高,根據課程性質的不同安排不同的課時,且特殊課程安排在指定的時間較為妥當(如體育課安排在下午最后的課時),從而保證學生在上其他課程時有良好的學習狀態;

(4)中學會區分班主任老師,每個班級至少需要一名班主任老師任課,并且一名班主任老師同時只能在一個班級任職班主任.

1 排課問題的模型及模擬退火算法

1.1 排課問題的模型及模擬退火算法

根據學校教學計劃,將一個年級所有班級一周的時刻表在一個平面上展開,用 (ci,lj)表示平面上的單元格,即第i個班級第j節課時,用C表示所有班級的集合,L表示一周內上課的課時集合,則設所有老師的集合為T,排課的實質就是向所有的(ci,lj)單元格中填且僅填入一位老師并且保證課程表在完全滿足所有的硬約束的條件下,盡量滿足軟約束條件.其中硬約束和軟約束條件歸納如下[9].

硬約束:

(1)全體老師必須完成教學計劃中的所有課時,即課程表不能有空缺單元格;

(2)同一位老師不能在相同的課時在不同的班級同時有教學任務;

(3)一個班級不能安排不同的老師上同一門課程;

(4)一個單元格只能安排一位老師;

(5)班主任數目必須與班級數目相等,且各班至少分配一名不同的班主任老師任課.

軟約束:

(1)體育課盡量安排在下午的最后兩節課;

(2)盡量不安排課程連堂上;

(3)不同性質的課程,應該酌情分配在不同的時間.例如,主干課程盡量安排在上午1、2節學習效率較高的時段.

(4)其他差異性需求,例如:需要課程連堂,部分老師需要固定的時間段等.

1.2 模擬退火算法

模擬退火算法由Kirkpatrick于1983年提出[10],算法主要用于求解大規模組合優化問題,特別是針對NP完全組合優化問題的求解.本文基于模擬退火算法的框架,對于排課這種特殊問題,通過改進其鄰域結構的產生策略,從而生成一套高效的求解中學排課問題的方案.

模擬退火算法思路來源于物理學中的模擬退火冶金時采用的Metropolis準則,簡而言之,算法的核心思想是隨著迭代次數的增加,產生較差的解被接受的概率也越來越小,而產生的較優解一直被接受.

原始模擬退火算法在求解組合優化問題時,采用的是一種高度隨機產生鄰域結構的策略,算法的迭代次數較長,收斂較慢.

1.2 排課問題的模型及模擬退火算法

(1)基礎方案

將硬約束條件(2),同一位老師不能同時在不同的班級上課,看成軟約束條件,其他條件保持不變,由此可生成一張中學課表的解,且該解可能不可行.然后利用模擬退火算法,每次迭代時隨機選擇同一班級的兩門課時進行交換,并按照退火算法中的Metropolis準則決定是否保留變換之后的課表.

(2)改進方案

模擬退火算法的缺點在于過多的迭代次數,算法的效率較低.基礎方案中隨機挑選交換課時是導致迭代緩慢的根本原因.人工排課過程可描述為先編排出帶有沖突的課表,然后解決沖突,再調整連堂課時,最后全局調優課表.本文基于人工排課的思想提出一種分階段的課表鄰域變化優化策略,有針對性的、目的性的在退火過程中加入“人工干預”.

2 算法實現步驟

2.1 衡量排課質量的優劣

使設課表S對應的代價值為f (S),有:

其中,T 為該年級老師總數; ti表示第 i位老師; 將中學課程分成7種不同的性質:語、數、外、體、文、理、其他,根據軟約束條件的第(3)條定義二維數組dc[k][j]表示第k門性質的課程被安排在第j課時產生的代價值;i表示該位老師任教的課程性質索引號;設老師已安排的單元格屬性為 arrangeCells,則記老師連堂的單元格屬性則記老師沖突的單元屬性 conflictCells ,則Q1、Q2分別代表連堂和沖突的代價值常數.

當f(S)值越小時,則課表S越合理.

2.2 生成初始解并優化解

2.2.1 劃分班級

為了滿足硬約束條件中的(3)和(5),可按如下步驟分配老師任課班級:

Step2.若老師 ti為班主任,則其中表示老師ti的任課班級集合.老師ti的任教課程為 COi,若則

Step3.若 ,則返回 Step2 繼續遍歷老師集合,否則轉入下一步;

Step5.對于第k門課程,統計任教該課程的所有老師索引號集合TIL;

Step6.遍歷TIL中老師的CLL集合,生成由Step2產生的對于第k門課程已分配的班級號集合CIL;

Step9.根據老師的教授班級數目屬性,對TIL中的老師按照順序分配每位老師的任課班級加入老師的CLL集合中;

Step10.k++,如果 k≤N,則返回 Step5,否則班級分配完成,退出循環.

2.2.2 生成帶有沖突的課表

為了滿足軟約束的第(1)條,可將任教特殊性質課程(如體育課)的老師放在老師集合的首位,其他老師按照一周內總上課課時數目從多到少排序.

由上一節的劃分班級,可以得到每個班級具體由哪些老師授課.為了滿足硬約束條件(1),對于每一位老師,根據其在每個班級一周上課課時數目的屬性,分配對應數量的該班級課時,并將所有分配的單元格記錄到對應老師的arrangeCells屬性中; 為了滿足硬約束條件(4),設計一張班級禁忌表,用于判斷該班級的每個課時是否已被分配.對于每個可分配的課時,通過dc[k][j]獲取固定代價值,通過老師一周中已上課的課時weeky屬性決定是否額外添加連堂代價值或沖突代價值,若發生沖突,則將該老師的 conflictCells屬性不重復的添加發生沖突的兩個單元格.通過遍歷老師的arrangeCells屬性,填充二維數組 sheetInfo[ci][lj],其值表示在 ci班,li課時任課老師索引號.連堂屬性arrangeCells可以由sheetInfo遍歷來獲取.

2.2.3 解決沖突并優化課表

模擬退火算法的關鍵步驟在于改變鄰域結構,產生新解,并以不同的概率接受新解.針對中學排課問題,本文將退火過程分為三個不同的階段,采用三種不同的鄰域異化操作.

(1)退火第一階段

這一階段僅作用于發生沖突的單元格,改變初始解結構,生成可行解.算法步驟如下:

Step2.遍歷教師t所有的單元格,獲取沖突所在的課時集合對應沖突課時li所在的班級是所有發生沖突的班級的集合,與FLL一一對應;

Step3.令 k=1;

Step4.令 i=1;

Step5.對于 lk和獲取滿足

?lx∈ ALL,sheetInfo[ci][lx]≠ sheetInfo[??ci][lk]

&sheetInfo[??ci][lx]≠ sheetInfo[ci][lk],其中*表示所有班級表示除ci班以外的班級,ALL集合表示在ci班中能與lk交換且不使交換的兩處位置發生沖突的所有課時集合;

Step6.剔除ALL中包含與特殊性質課程交換的課時,再依據交換后是否與周圍課時連堂而產生額外代價,采用輪盤賭的方式擇優選擇一個交換課時,加入備選交換課時集合PY中;

Step8.隨機選擇PY中的優選課時對各班進行交換,選擇的個數為更新sheetInfo以及發生變化的位置處的老師各個屬性值;

退火第一階段解決了初始化課表中所有發生沖突的位置,課表的整體代價值必然是減少的,算法也一定會接受這些改變.

(2)退火第二階段

這一階段著力解決存在連堂的單元格,并且保證變化后的解仍為可行解.算法步驟類似于退火第一階段,區別在于觀察的是老師的屬性.當分離了連堂的單元格,課表的整體代價值必然減少,算法也會接受該解; 當程序無法分離連堂單元格時,自動轉入退火第三階段.

(3)退火第三階段

該階段處于退火的最后一個階段,采用全隨機方案優化課表結構,產生代價值更小的解.算法步驟如下:

Step1.隨機獲取一個班級c,并置是否交換參數s為假;

Step2.初始化循環次數常量N;

Step5.若 s為假則轉入 Step6,否則轉入 Step7;

Step8.返回退火框架更新優解結構、溫度以及迭代次數信息,判斷是否退出該階段.

本文中模擬退火算法的內外層循環的終止準則均采用循環總數控制法,退火總框架偽代碼如下:

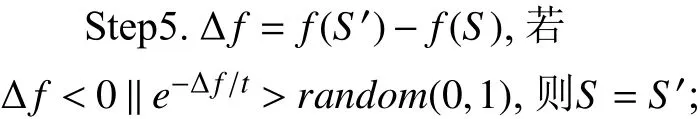
3 數據實驗結果

本文采用模擬院校數據:12門課程; 50位老師;15 個班級; 每天上午有 4 節課,下午有 3 節課; 每周有六天上課時間,其中周六只安排上午課程,下午不安排課程; 一共需要安排 585 節課.為了對比的有效性,修改2.2.1節的Step7,生成列表后不亂序,即保證每次老師被分配到的班級一致,通過控制變量法來比較不同的排課方案在求解中學排課問題的效率.

實驗硬件環境為PC機,配置為Inter(R)Core(TM)i3 CPU,4G RAM; 軟件平臺為 Eclipse Mars.1,數據存儲在Mysql數據庫中,基于Java語言編程.

表1通過保持其他參數不變,改變降溫次數T和迭代步長N,即控制算法的外層和內層的循環次數.經過重復5次實驗取時間和最優解的平均值得到兩種算法實驗結果對比表.

表1 兩種算法運行效率對比表

由表1中的數據可以看出當總循環次數在100左右時,基礎排課方案很難找到不發生沖突的課表,而改進的分段模擬退火算法可以快速找到可行解; 改進的方案較基礎方案在運行時間上也有提高; 兩種算法在求得最優解結果上基本保持一致.

取(T,N)=(250,50),橫坐標為(T*N),縱坐標為總代價值,為便于觀察前期兩種算法迭代結果的不同,可將橫坐標取對數,繪于圖1.

由圖1可以看出本例中基于改進方案的模擬退火算法在解決中學排課問題中收斂速度比基于基礎方案退火算法快接近10倍; 兩種方案最后產生的最優解值相近.

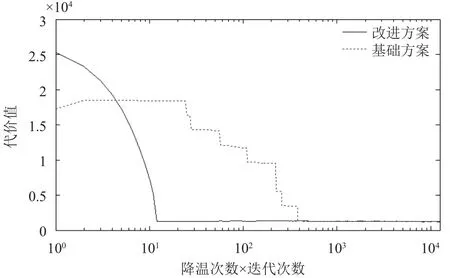
圖1 改進前后方案尋優半對數曲線圖

4 排課系統

在實際應用中,中學排課問題的軟約束條件更加復雜.為了滿足軟約束(4),即多元化的排課需求,本系統基于 SSM(Spring,SpringMVC,Mybatis)框架提供可以和用戶交互的機制.

4.1 前端顯示模塊

前端利用JQuery編寫數據錄入邏輯以及校驗邏輯的代碼.如圖2所示.

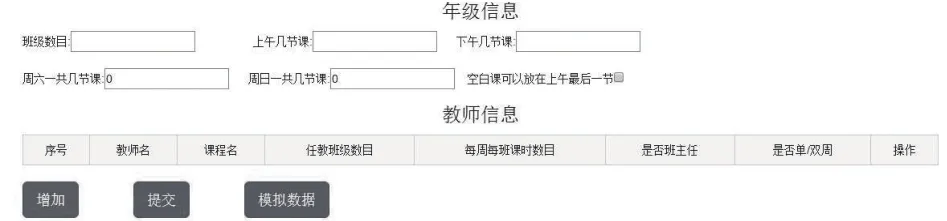
圖2 前端顯示

合法性校驗主要包括:班主任數目=班級數目; 輸入不為空.

4.2 模擬數據模塊

數據庫連接池由Spring框架托管,并通過Mybatis框架從后臺服務器的數據庫中調用一組模擬數據,自動填充圖2所示的所有表單字段,用于快速模擬排課流程.表單提交至deal.action后臺路徑,由后臺處理并返回至result.jsp頁面中.

4.3 前端調整模塊

如圖3所示在result.jsp頁面中,鼠標懸停單元格以查看教師詳情.利用html5的拖拽特性,允許用戶手動調整課程單元格,單擊單元格變色固定再次提交后臺處理.

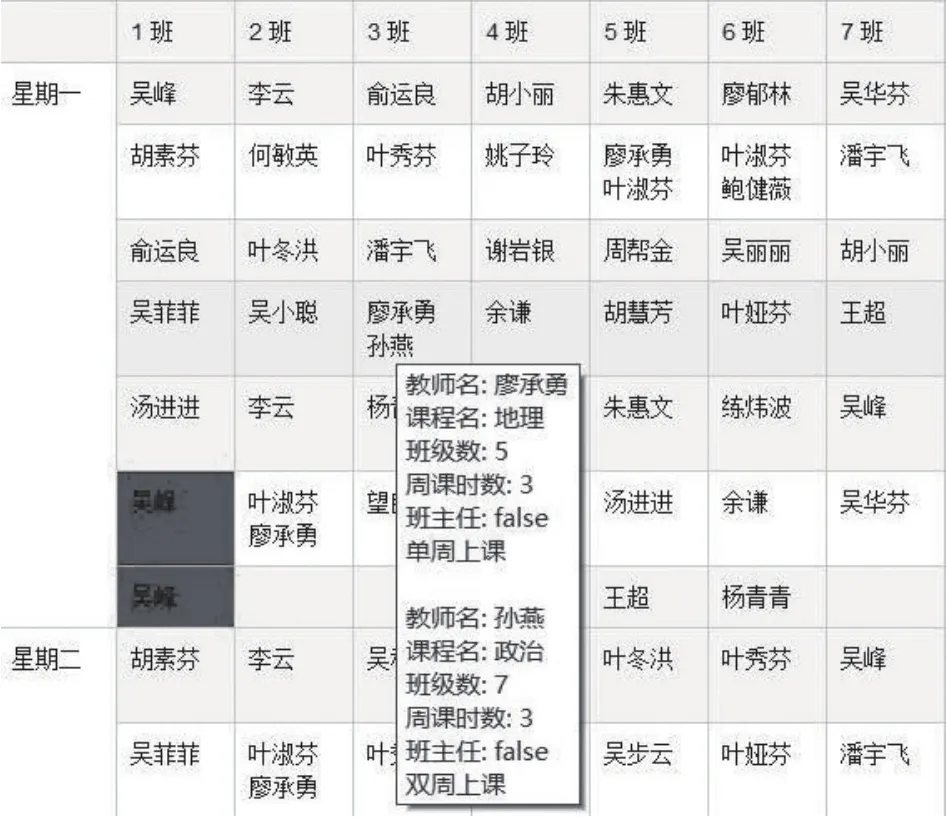
圖3 調整并固定單元格

圖3 顯示了得到一次后臺處理結果之后,人為調整,即將兩節“吳峰”的語文課程固定.前端記錄調整信息并提交至后臺change.action,后臺模擬用戶調整行為,并解決沖突、優化課表,最后返回結果至result.jsp頁面中.重復以上動作,即可生成帶有人工干預的個性化課表.

4.3 后臺處理模塊

將前端輸入數據字段名稱規范化,基于SpringMVC框架即可自動將傳入的數據轉換成POJO,節省開發成本[11].

根據不同的action使用不同階段的模擬退火算法.對于deal.action,應用第一階段模擬退火算法生成可行解,應用第二階段模擬退火算法指向性優化解,應用第三階段模擬退火算法隨機優化解; 對于change.action,只使用前兩個階段的模擬退火算法生成并優化解,因為第三階段的退火過程會隨機全局打亂課表,導致調整后課表其他單元格可能會發生較大的差異,即用戶為了滿足特殊需求調整的課表方案無需經過退火第三階段處理.如圖4是對圖3調整后的處理結果.

5 結束語

分階段的模擬退火算法在解決中學排課問題中,根據當前的課表狀態,采用不同的鄰域異化操作,可以快速生成可行課表,全局搜索優化課表并達到收斂.為了滿足對于課表的更多復雜需求,基于本文中提出的改進后的模擬退火算法,設計了一套完整的可以與用戶交互的系統,并投放于生產環境中.

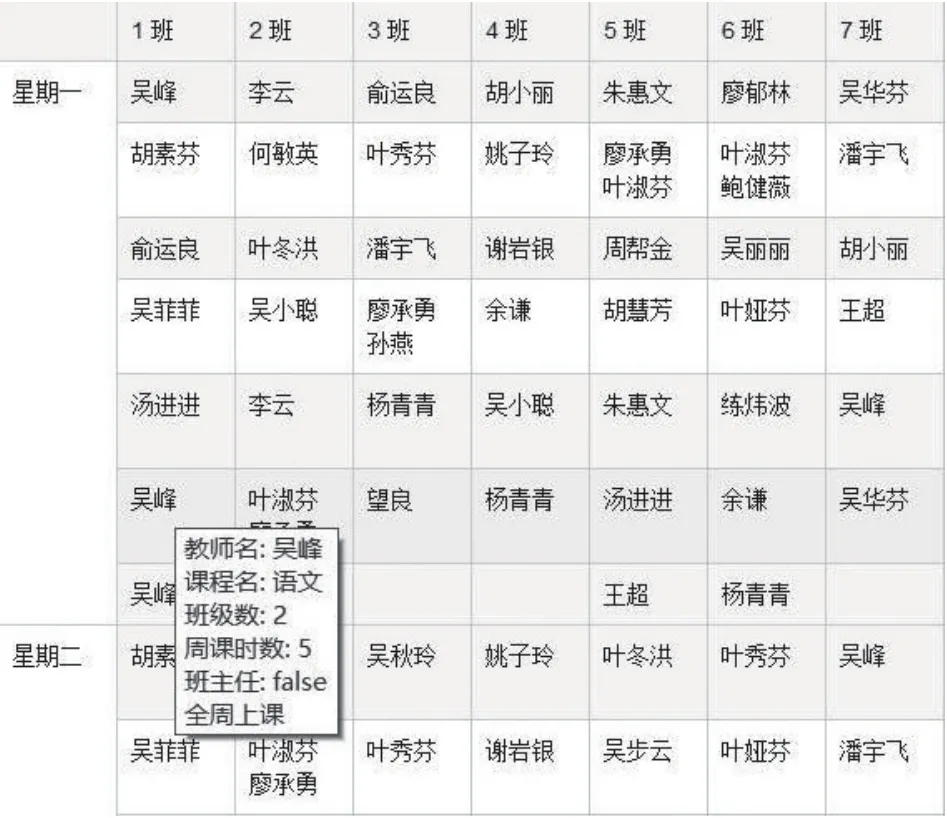
圖4 后臺處理結果

1Even S,Itai A,Shamir A.On the complexity of timetable and multicommodity flow problems.SIAM Journal on Computing,1976,5(4):691–703.[doi:10.1137/0205048]

2趙玉新,Yang XS,劉利強.新興元啟發式優化方法.北京:科學出版社,2013.

3張健.基于圖論的高校排課系統實現.重慶師范大學學報(自然科學版),2005,22(1):35–38.

4許琦.基于遺傳算法的高校排課問題的研究[碩士學位論文].廣州:華南理工大學,2012.

5祝勇仁,曹煥亞.應用遺傳算法求解排課問題.計算機應用與軟件,2007,24(12):130–132,141.[doi:10.3969/j.issn.1000-386X.2007.12.051]

6李增智,王云嵐,陳靖.課程表問題的一種混合型模擬退火算法.西安交通大學學報,2003,37(4):343–345,350.

7陳本慶,馬永強,何虎.改進型回溯法在高校排課中的應用.成都信息工程學院學報,2003,18(2):150–154.

8趙惠怡.基于蟻群算法的排課問題的研究[碩士學位論文].遼寧:大連海事大學,2007.

9姜謙.中小學排課系統的研究與設計[碩士學位論文].廣州:華南理工大學,2010.

10Kirpatrick S,Gelatt CD,Vecchi MP.Optimization by simulated annealing.Science,1983,220(4598):671–680.[doi:10.1126/science.220.4598.671]

11吳婉楠.基于SpringMVC和MyBatis框架的炒股比賽系統的設計與實現[碩士學位論文].南京:南京大學,2016.

Application of Simulated Anneal Algorithm for Curriculum Schedule Problem in Senior High Schools

TANG Huan,GAO Jian

(School of Mechatronic Engineering and Automation,Shanghai University,Shanghai 200072,China)

A solution of staged simulated annealing is proposed to settle the schedule problem of senior high schools.The difficulty of the problem mainly lies in how to solve lots of conflicts existing in the schedule and how to optimize it.We initialize a schedule with conflicts randomly,and dissimilate the structure of the solution with artificial intervention to make the schedule feasible in the first stage.In the second stage,we try to make the schedule meet general constraints by instructively changing the structure of the schedule.In the third stage,we generate optimized solution through varying the schedule with heuristic dissimilate random field employed.In order to meet the demand for diversified schedule,the actual production environment in the user interface provides the manual adjustment to the schedule.It is found that the improved simulated annealing algorithm has a faster convergence speed,and higher operation efficiency in solving curriculum schedule problem of senior high schools and in the case of less number of iterations,it can also generate a feasible solution.

simulated annealing; curriculum schedule problem; artificial intelligent

唐環,高健.在中學排課問題中實用的模擬退火算法應用.計算機系統應用,2017,26(10):225–230.http://www.c-s-a.org.cn/1003-3254/6059.html

2017-02-11; 采用時間:2017-03-22