解題能力是學生必備素質
——運用還原法提高高中數學解題準確性的對策分析

崔一華

解題能力是學生必備素質
——運用還原法提高高中數學解題準確性的對策分析

崔一華

在高中數學的學習當中，解題能力是受教育者必備的素質之一。高中數學的解題方法有很多，還原法也是其中之一，能夠有效地提升解題準確性。此文從運用還原法解決幾何類題、運用還原法解決公式定理題以及運用還原法解決技巧性較強的題這三方面對運用還原法提高高中數學解題準確性的對策進行了分析。

解題能力；高中數學；還原法；幾何題；公式定理；準確性

隨著教育事業的不斷發展，對高中受教育者的數學能力的要求也越來越高。數學是一門邏輯性很強的學科，可以鍛煉受教育者的思維能力。在高中數學的解題過程當中需要具備發散思維能力，多數受教育者會面臨各種各樣的困難，不知道從哪里下手找到解題的切入點，這便需要運用多種解題方法，還原法也是眾多方法之一，運用還原法來解決問題顯得尤為重要。在高中數學解題過程中巧妙地運用還原法可以提升解題的準確性，提升受教育者的解題能力。

一、 運用還原法解決幾何類題

在高中數學當中，空間立體幾何的三視圖是一項重要的內容，同時也是高考當中的高頻考點。受教育者在解決這類題型的時候，如果僅僅單憑分析題干，多數人很難解出答案，即便能夠分析出答案，也無法確保答案的準確性。

例如：下圖給出了一個幾何體的三視圖，那么下面這個幾何體的體積為多少？

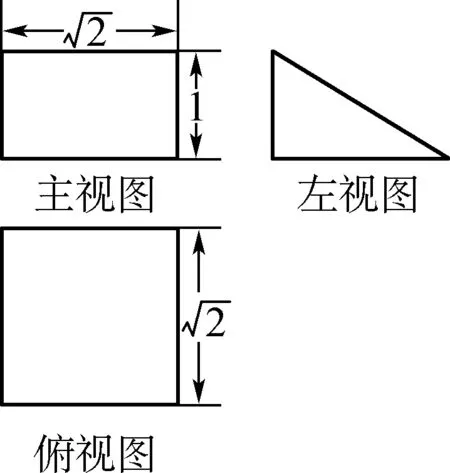
解析：如上圖所示，對于這種簡單的幾何體三視圖，單憑看圖雖也能夠計算出體積，但相對來說還是具有一定的抽象性，也未必有較高的準確性，對那些空間想象力較弱的受教育者來說，仍存在一定的難度。此時，便需要對空間幾何體的三視圖進行還原。在這個幾何體的三視圖當中呈現出了兩個矩形，通過規律可以得知圖當中的空間幾何體是柱體。通過觀察可發現左視圖是一個三角形，因此可以推斷這個空間幾何體是三棱柱，算出其體積是1。如此一來，運用還原法更容易計算，并且能夠提升準確性。

二、 運用還原法解決公式定理題

在高中數學的學習當中，公式定理十分關鍵，并且被廣泛地運用在解題當中，有一部分定理能夠正向地應用以及證明。然而，有很多題目當中體現的公式定理并不是顯而易見的，面對這樣類型的題目，多數受教育者并未將切入點放在題干當中的公式上面，沒有多加觀察，理不清思路，因此不知道應該采用怎樣的解題方法。這個時候便需要對題干進行細心觀察，多加分析，對已知條件當中的公式進行還原。

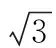
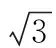
三、 運用還原法解決技巧性較強的題

在高中數學當中有很多技巧相對較難的題目，單憑表面來看，很難找到解題的切入點，令多數受教育者不知從而下手。在解決這種類型題目的時候，也可以運用還原法，有助于找到解題思路的關鍵點，從而令問題得到快速準確的解決。

例如：設定現在有四個數字，任意取其中三個數字的和，它們分別是40、60、72、80，試著求出這四個數字分別是多少。

解析：這種類型的數學題，在題干當中并未給出太多的已知條件，看上去基本上毫無聯系，因此技巧性較強。多數受教育者面對這種類型的題目的時候，往往一頭霧水，找不到頭緒，更不知從何下手。此時便可運用逆向思維進行還原，找到問題的切入點，題目當中既然已經明確了這四個數字當中任意三個數字的和，那么便可將四個數字的和設為x，通過觀察題意，找到已給條件間存在怎樣的聯系，這道題便很容易找到解。

將四個數字的和設成x，那么便可結合題意將這四個數字分別還原成x-40、x-60、x-72、x-80，并列出(x-40)+(x-60)+(x-72)+(x-80)=x，解得x=84，將x=84代入，因此便可得出這四個數字分別是44、24、12與4，將答案還原于題干當中，44+24+12=80，24+12+4=40，44+24+4=72，44+12+4=60，如此可見，與題意相符。運用還原法解答這樣的技巧性問題，不但可以快速理清題意從而找出解題方法，還能夠提升解題的準確性，提升受教育者的解題能力。

四、 結束語

綜上所述，在對高中數學的解題過程當中，運用還原法是一種有效的解題方法，這種方法能夠將原本抽象且很難找到切入點的問題變得清晰直觀。在實際的教學當中，廣大高中數學教育者應當將還原法有效地運用于數學解題當中，提升解題的準確性，令受教育者的解題能力得到提升，與此同時，還要對相關對策展開積極的探究，獲得更加顯著的教學成效。

[1]李兆強.高中數學數列的解題常規方法分析[J].數理化學習(高中版)，2015，(7)：2-3.

[2]徐崇明.淺談高中數學解題思維方法教學策略[J].新課程導學，2016，(26).

崔一華，江蘇省寶應中學。