基于均勻化混沌系統生成S盒的算法研究

臧鴻雁 黃慧芳

?

基于均勻化混沌系統生成S盒的算法研究

臧鴻雁①黃慧芳*②

①(北京科技大學數理學院 北京 100083)②(廈門大學嘉庚學院信息科學與技術學院 漳州 363105)

該文給出了一個新的二次多項式混沌系統，并利用系統與Tent映射拓撲共軛的性質，給出了系統的概率密度函數，基于概率密度的形式，進一步設計了一個變換函數，實現了系統的均勻化。針對均勻化前后的混沌系統構造了S盒生成算法，對該算法產生的300個S盒進行差分概率(DP)和線性概率(LP)的統計分析，結果表明均勻化后混沌系統產生的S盒的DP和LP略優于均勻化前的值。

混沌系統；均勻化；拓撲共軛；S盒

1 引言

1975年，Li等人[1]發表了著名的“周期三蘊含混沌”一文，首次用數學定義描述了“混沌”一詞。通過研究混沌系統的復雜非線性動力學現象能夠發現其具有偽隨機性、遍歷性和初值敏感性等特性。自1989年，Matthews[2]提出“混沌密碼”后，人們對混沌系統及其應用的了解越來越深入。密碼學家分析得出一個好的密碼系統本質上也是一個混沌系統的結論[3]。這一發現挖掘了混沌在密碼學領域內的應用潛力，自20世紀80年代以來該領域成為了日益熱門的研究方向[4]。

混沌系統具有各態歷經的特性，利用混沌映射的概率密度可以描述系統長期的統計特征。文獻[5]通過證明Logistic映射與Tent映射的拓撲共軛關系以及Chebyshev映射與Tent映射的拓撲共軛關系，推出了Logistic映射和Chebyshev映射的概率密度。通過混沌映射的概率密度函數可以發現大部分混沌序列不服從均勻分布。2011年，文獻[6]中給出了一個將Logistic混沌序列轉化為服從均勻分布的隨機序列生成方法。

S盒是多數分組密碼中的唯一非線性部件，設計具有良好性能的S盒是分組密碼算法設計的關鍵要素之一。一個S盒本質上可以看作映射，或者可以寫作：，它是將位輸入映射到位輸出的非線性映射。構造動態S盒的方法有很多[7]，利用混沌系統良好的偽隨機性質來構造動態S盒已經成為構造S盒的一個重要方法[8]。

本文利用文獻[9]提出的一般二次多項式映射存在3-周期點的充分必要條件構造了一個新的二次多項式混沌系統，并依據該系統與Tent映射拓撲共軛的性質，給出了系統的概率密度函數，在此概率密度的基礎上對該系統進行了均勻化處理；分別利用均勻化前后的混沌系統設計了動態S盒生成算法，對算法生成的300個S盒的性能指標進行統計分析，發現利用均勻化后系統能夠產生性能更好的S盒。

本文其余部分安排如下：在第2節中提出了一個新的混沌系統，并基于概率密度函數對系統進行了均勻化處理。在第3節中，對均勻化前后的混沌系統進行了統計直方圖和熵的對比分析。第4節中設計了一個動態S盒的生成方法，利用均勻化前后的混沌系統分別產生了300個S盒，并進行了S盒性能的對比。第5節總結全文。

2 二次多項式混沌系統的均勻化處理

文獻[9]提出了一般非線性二次多項式的3-周期點的等價命題。

引理1[9]二次多項式有實的3-周期點的充分必要條件是。

定義1[10]設和為兩個映射，如果存在一個可逆映射，使得成立，則稱和是拓撲共軛的。此處表示兩個映射的復合。

拓撲共軛是動力系統中的重要理論。如果兩個系統滿足拓撲共軛關系，則它們具有相同的動力行為。

基于引理1，本文構造了新的1維混沌系統為

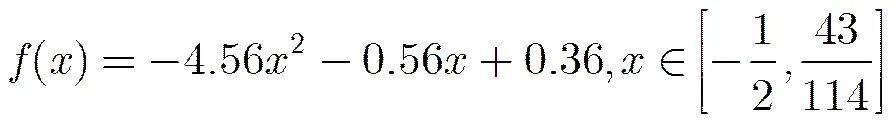
將系統表示為

(2)

定理1 混沌系統

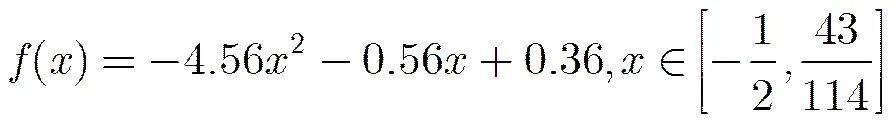
與Tent映射是拓撲共軛的。

令Tent映射

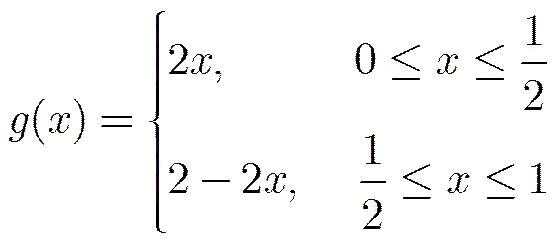
和連續可逆函數

(5)

定理2 混沌系統

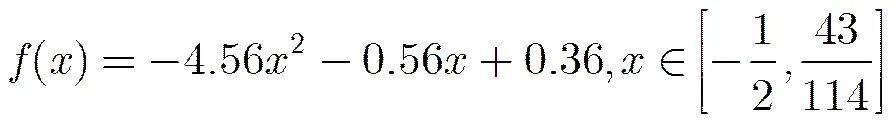
的概率密度函數為

(7)

(8)

由系統式(1)的概率密度函數可知，該二次多項式混沌系統產生的序列不是均勻分布的，意味著其產生的混沌序列容易具有明顯的統計特性，不利于推廣應用。為了使其服從均勻分布，以下對式(1)進行均勻化處理。

則隨機變量為

(10)

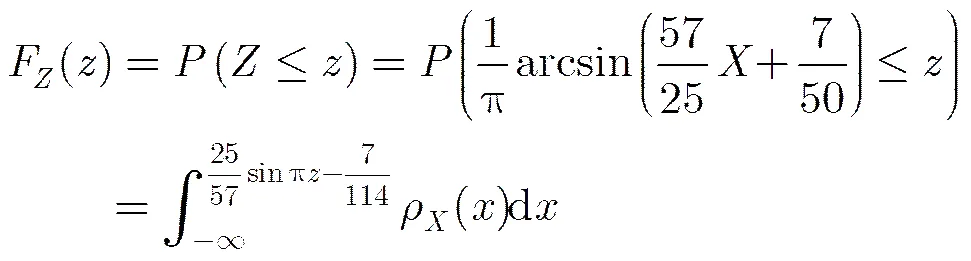
(12)

以上是利用原混沌系統的概率密度函數對其進行均勻化處理的方法。由證明過程可知，在文中給定區間內，均勻分布的隨機變量與原隨機變量滿足一一對應關系，因為是式(1)混沌系統的變量，從而系統

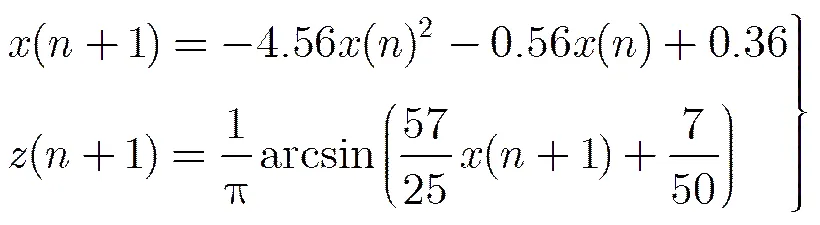
必是混沌系統，并且與式(1)系統有著相同的Lyapunov指數。

3 二次多項式混沌系統的熵分析

以下針對均勻化前混沌系統式(1)和均勻化后系統式(13)產生的序列從直方圖統計、信息熵和離散熵等方面進行了分析，驗證均勻化方法的有效性。

3.1 統計分析

圖1(a)是均勻化前混沌系統生成的序列的統計直方圖，圖1(b)是均勻化后反三角函數生成的序列的統計直方圖。由對比圖可見，處理后的混沌序列均勻性明顯增強。

3.2 信息熵分析

信息熵是信息論中用以度量信源不確定性程度的概念，最早由香農提出。以下是本文中均勻化前后系統產生的混沌序列的信息熵檢測。令離散混沌序列長度為，將式(13)迭代得到的離散混沌序列，將序列值域等分成個區間，統計落在每個區間內的值的個數，記為。計算每個區間的統計概率，有。根據最大信息熵原理，信息熵最大值為，其中表示統計區間個數，對應通信系統中的信源符號數。下面選定序列長度，分別測試時均勻化前后序列的信息熵與最大熵，比較結果如表1。

表1 均勻化前后混沌序列的信息熵對比

3.3 離散熵分析

2007年Amigo等人[11]基于排列熵(PE)定義，提出了有限集合上的離散熵(DE)的概念，可替代拓撲熵衡量系統的混沌程度。該定義為

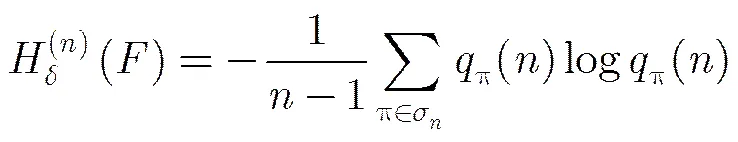
從圖2(a)、圖2(c)、圖2(e)中式(1)系統的熵和離散熵圖像可以看出，系統離散熵近似于熵偏移固定長度后的圖像，這也從某種程度說明，離散熵能夠有效衡量系統的混沌程度；圖2(b)、圖2(d)、圖2(f)顯示均勻化前后系統的離散熵完全相同，圖2表明，經過本文中的均勻化方法處理之后，混沌系統的混沌特性不會被破壞，同時均勻性得到了有效的改善。

4 基于均勻化混沌系統構造S盒

本文分別利用均勻化前后的兩個混沌系統式(1)和式(13)設計動態S盒生成算法，并對兩組S盒進行統計分析和性能檢測。具體的算法和分析結果如下。

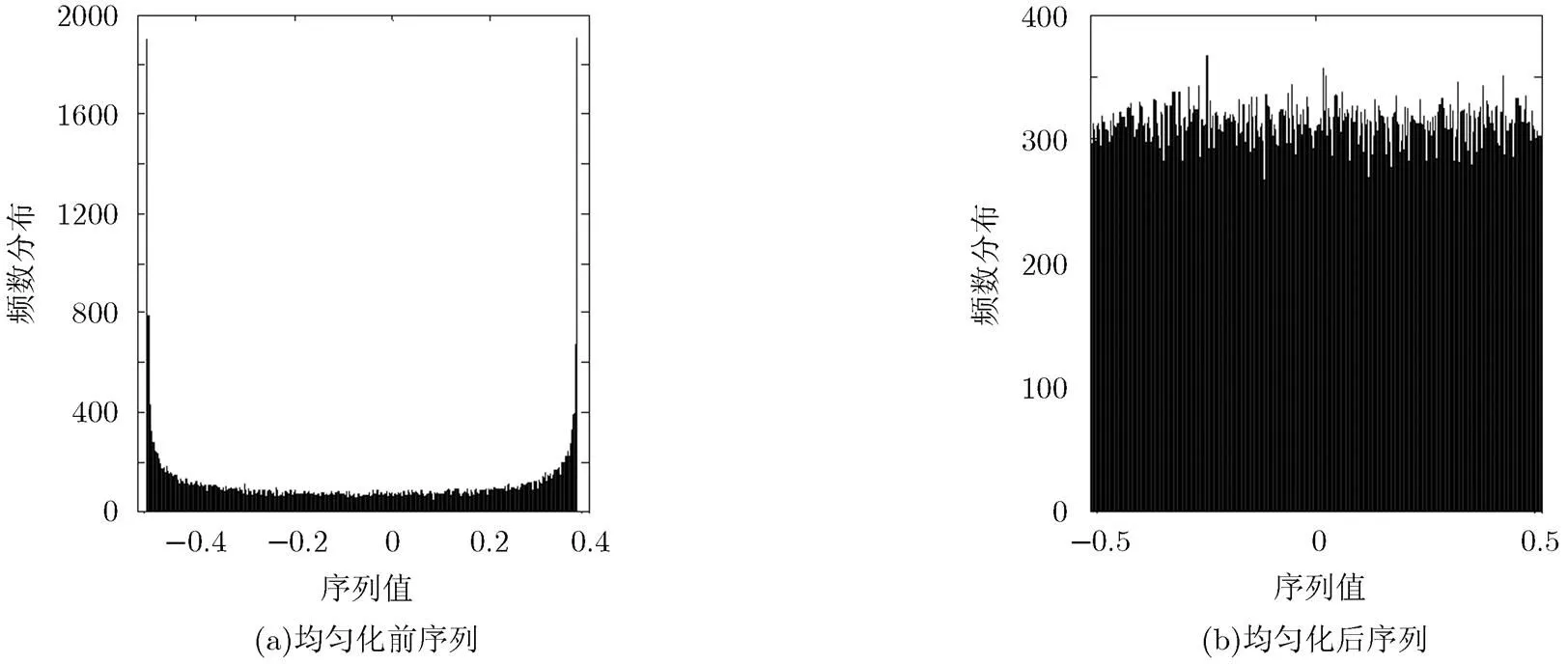
圖1 統計直方圖

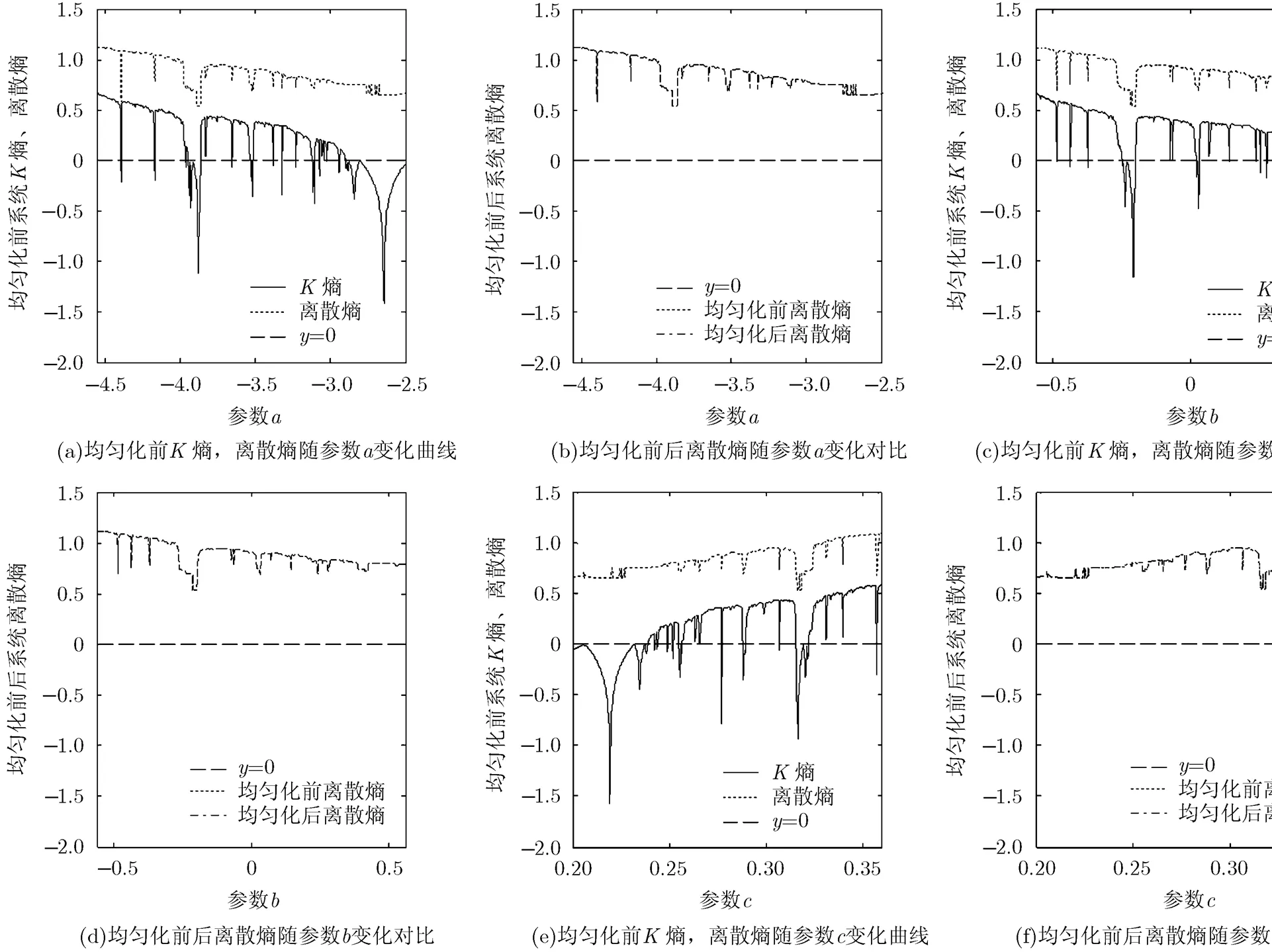
圖2 均勻化前后系統K熵與離散熵分析對比圖

4.1 S盒算法構造

(4)從前往后依次取位置序列中不相等的256個變量作為最終的S盒序列。

在保持算法中參數一致的情況下，將步驟(2)中產生置亂效果的混沌系統分別用均勻化前的式(1)系統和均勻化后的式(13)系統替換，基于不同的初始值動態生成S盒序列。

檢測生成的300個混沌S盒的差分概率(DP)和線性概率(LP)，并統計各個指標值對應的S盒的個數，作直方圖如下，其中圖3為利用均勻化前混沌系統生成的S盒的統計。圖4為利用均勻化后混沌系統生成的S盒的統計。

差分概率(DP)用以度量S盒抵抗差分密碼攻擊的能力，DP越小，S盒越能夠抵抗差分攻擊。而線性概率(LP)用來度量S盒對于線性密碼攻擊的抵抗能力，LP越小，抵抗能力越強。從兩個圖的對比中可以看出，基于均勻化后混沌系統生成的DP, LP指標值較好的S盒數量相對更多，進一步說明本文提出的均勻化方法可以有效地改善混沌系統的均勻性，并保持良好的混沌特性。

4.2 S盒性能分析

下面從均勻化后的混沌系統構造生成的S盒中選取出一個DP, LP指標值良好的進行其他密碼學性能分析，并且與近兩年內發表的文獻中構造的混沌S盒進行對比，檢驗本文構造生成的S盒是否適用于分組密碼算法設計中。

表2為選取的均勻化后混沌系統生成的S盒序列。對該S盒的雙射特性，非線性度，嚴格雪崩準則，輸出比特間獨立性，差分概率，線性概率和Lyapunov指數等指標依次進行分析。

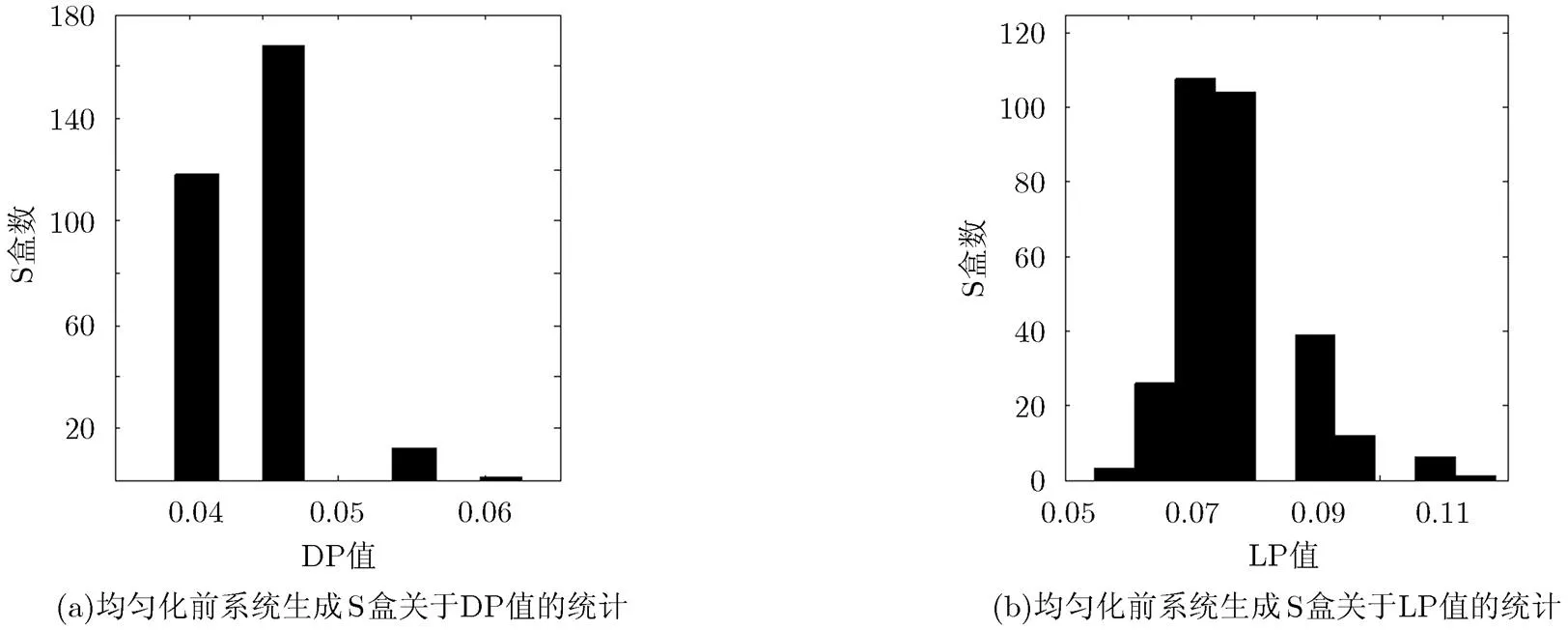
圖3 均勻化前系統生成S盒數

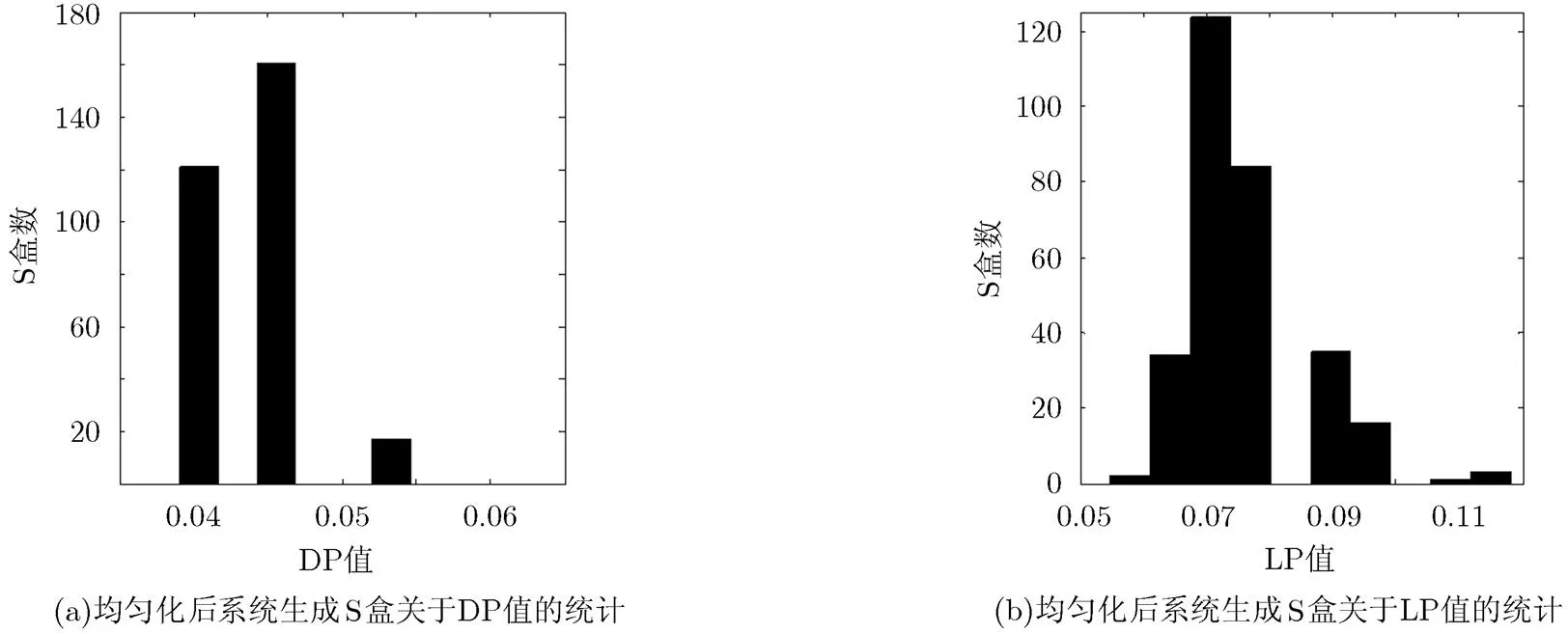
圖4 均勻化后系統生成S盒數

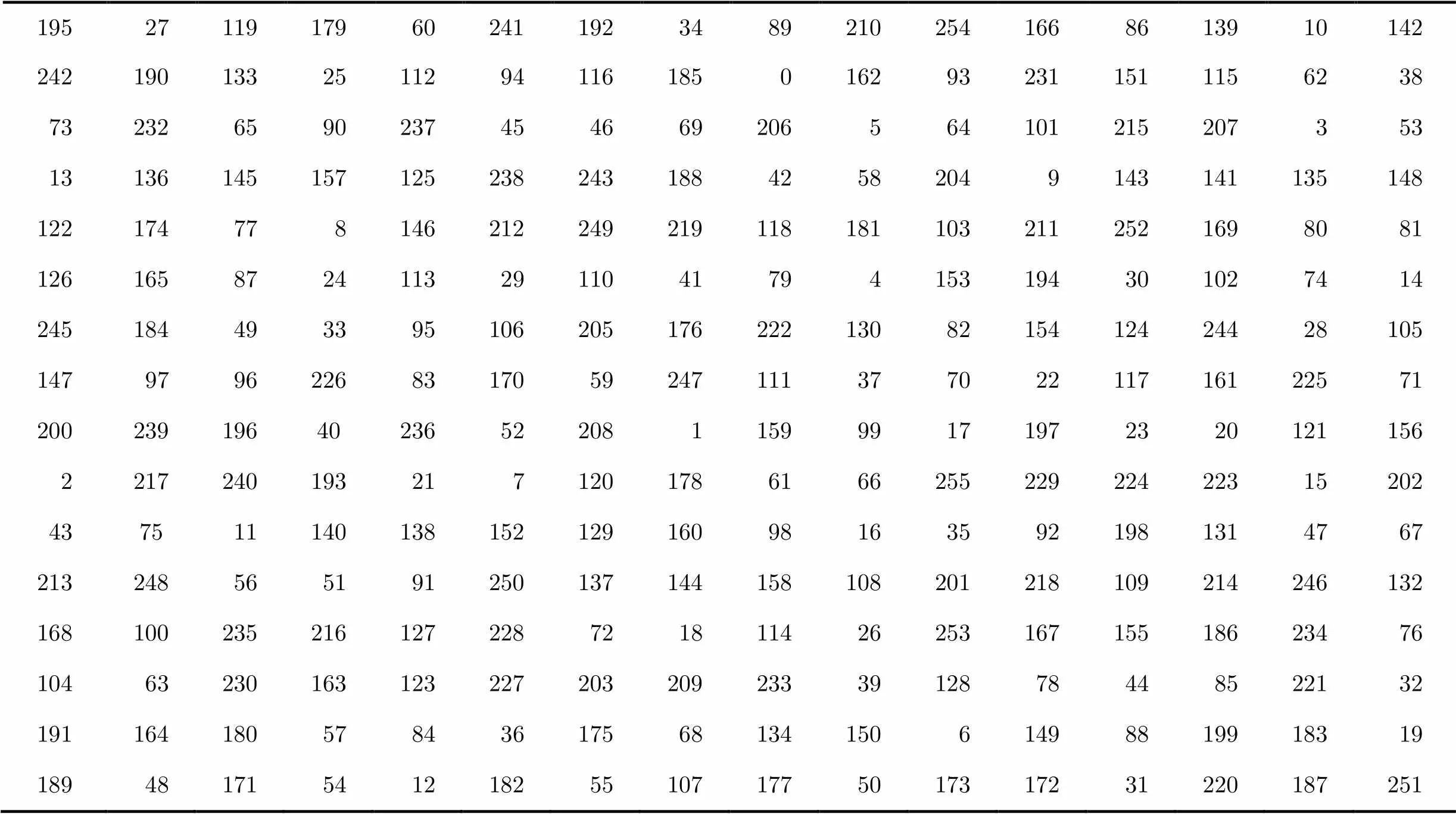
表2 均勻化混沌系統式(13)生成的S盒序列

對雙射特性進行檢測，S盒8個分量布爾函數的線性運算之和都為128，充分滿足雙射特性。

檢測S盒的嚴格雪崩準則和輸出比特獨立性時，直接看相關矩陣對比可能不能直觀看出差距。為了比較滿足嚴格雪崩效應的程度，利用公式估計了相關矩陣與理論值0.5的偏移量，將第1個相關矩陣的偏移量記為，第2個相關矩陣與0.5理論值的偏移量記為。本文構造的S盒與現有S盒的兩個偏移量的比較如表3所示。我們希望S盒的相關矩陣元素與理論值越接近越好，也就是偏移量越小越好。從表3的對比結果可見，本文S盒較好地滿足嚴格雪崩準則和輸出比特間獨立性。

表3 S盒的對比

表3 S盒的對比

S盒 均勻化后系統生成的S盒0.033453130.01692857 文獻[12]中的S盒0.060421870.01771428 文獻[13]中的S盒0.039156250.01664286 文獻[14]中的S盒0.034718750.01546429

利用文獻[15]中提出的S盒的Lyapunov指數定義，映射的離散Lyapunov指數揭示的是雙射映射中自變量改變1 bit時，狀態值變化位數的情況[15]。因而 Lyapunov指數越大，說明自變量改變引起的函數值變化越大，混亂程度越高。本文構造S盒的DP, LP及其Lyapunov指數結果與文獻中結果的對比見表4。

表4 S盒的指數對比

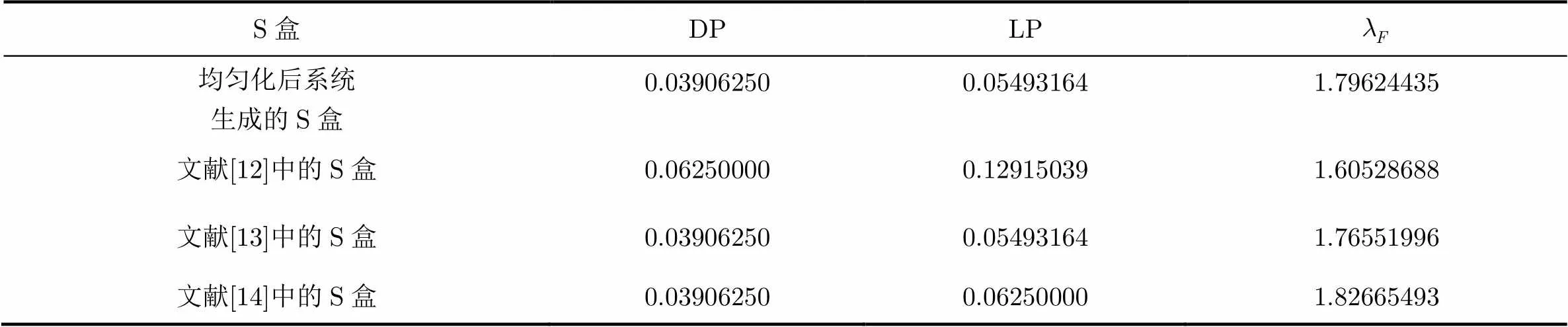
表4 S盒的指數對比

S盒DPLP 均勻化后系統生成的S盒0.039062500.054931641.79624435 文獻[12]中的S盒0.062500000.129150391.60528688 文獻[13]中的S盒0.039062500.054931641.76551996 文獻[14]中的S盒0.039062500.062500001.82665493

5 結論

本文提出了一個新的二次多項式混沌系統，利用拓撲共軛理論給出了系統的概率密度函數，進一步提出一個變換函數對系統進行了均勻化處理。為了驗證均勻化方法的效果，對均勻化前后系統生成的混沌序列進行了直方圖統計、信息熵分析和離散熵分析。分析結果表明了均勻化方法的有效性。本文基于混沌系統設計了一個新的構造S盒的算法，利用均勻化前后的混沌系統分別生成兩組各300個S盒并對其DP, LP指標進行統計分析。通過差分及線性攻擊的分析對比可見，本文均勻化方法處理的混沌系統能夠產生密碼性更好的S盒。這些S盒可以為進一步設計分組密碼算法提供良好的非線性資源。

[1] LI Tienyien and YORKE J A. Period three implies chaos[J]., 1975(82): 985-992.

[2] MATTHEWS R. On the serivation of a “chaotic” encryption algorithm[J]., 1989, 13(1): 29-42.

[3] GOTZ M, KELBER K, and SCHWARZ W. Discrete-time chaotic coders for information encryption--Part 1: Systematic structural design[C]. Workshop on Nonlinear Dynamics of Electronic Systems, Moscow, Russia, 1997: 21-26.

[4] KOCAREV L, JAKIMOSKI G, STOJANOVSKI T,. From chaotic maps to encryption schemes[C]. IEEE International Symposium on Circuits, & Systems. Monterey, USA, 1998: 514-517.

[5] 何振亞, 李克, 楊綠溪. 具有良好安全性能的混沌映射二進制序列[J]. 電子與科學學刊, 1999, 21(5): 646-651.

HE Zhenya, LI Ke, and YANG Luxi. Chaotic Map Binary Sequences with Good Security[J]., 1999, 21(5): 646-651.

[6] 曹光輝, 胡凱, 佟維. 基于Logistic均勻分布圖像置亂方法[J]. 物理學報, 2011, 60(11): 125-132.

CAO Guanghui, HU Kai, and TONG Wei. Image scrambling based on logistic uniform distribution[J]., 2011, 60(11): 125-132.

[7] TERRY R. Substitution cipher with pseudo-random shuffling: The dynamic substitution combiner[J]., 1990, 14(4): 289-303.

[8] WONG K W, HO S W, and YUNG C K. A chaotic cryptography scheme for generating short cipher text[J]., 2003, 310(1): 67-73.

[9] 周海玲, 宋恩彬. 二次多項式映射的3-周期點判定[J]. 四川大學學報(自然科學版), 2009, 46(3): 561-564. doi: 103969/j. issn. 0490-6756.2009.03-009.

ZHOU H L and SONG E B. Discrimination of the 3-periodic points of a quadratic polynomial[J].(), 2009, 46(3): 561-564. doi: 103969/j.issn.0490-6756.2009.03-009.

[10] 郝柏林. 從拋物線談起--混沌動力學引論[M]. 第2版, 北京: 北京大學出版社, 2013, 114-118.

HAO B L. Starting with Parabola: An Introduction to Chaotic Dynamics[M]. 2nd Edition, Beijing: Peking University Press, 2013, 114-118.

[11] AMIGO J M, KOCAREV L, and TOMOVSKI I. Discrete entropy[J]., 2007, 228(1): 77-85.

[12] KHAN M, SHAH T, and BATOOL S I. Construction of S-box based on chaotic Boolean functions and its application in image encryption[J].&, 2016, 27(3): 677-685.

[13] 韓丹丹, 閔樂泉, 趙耿, 等. 一維魯棒混沌映射及S盒的設計[J]. 電子學報, 2015, 43(9): 1770-1775. doi: 10.3969/j.issn. 0372-2112.2015.09.014.

HAN D, MIN L, ZHAO G,. One-dimensional robust chaotic map and the construction of S-box[J]., 2015, 43(9): 1770-1775. doi: 10.3969/j. issn.0372-2112.2015.09.014.

[14] LIU G, YANG W, LIU W,. Designing S-boxes based on 3-D four-wing autonomous chaotic system[J]., 2015, 82(4): 1867-1877. doi: 10.1007/s11071-015- 2283-y.

[15] 臧鴻雁, 范修斌, 閔樂泉, 等. S-盒的 Lyapunov 指數研究[J]. 物理學報, 2012, 61(20): 200508.

ZANG H, FAN X, MIN L,. Research of Lyapunov exponent of S-boxes[J]., 2012, 61(20): 200508.

Research on Algorithm of Generating S-box Based on Uniform Chaotic System

ZANG Hongyan①HUANG Huifang②

①(,,100083,)②(,,363105,)

A new quadratic polynomial chaotic system is given and homogenized based on its probability density function. Then, based on the chaotic systems before and after homogenization, an S-box generation algorithm is constructed. By numerical simulation, the algorithm dynamically generates 300 S-boxes and then analyses their Differential Probability (DP) and Linear Probability (LP). The statistical results show that the uniform chaotic system can produce better performance of S-boxes.

Chaotic system; Homogenization; Topological conjugation; S-box

TN918. 1

A

1009-5896(2017)03-0575-07

10.11999/JEIT160535

2016-05-26；改回日期：2016-10-27；

2016-12-20

黃慧芳 13661363592@163.com

國家自然科學基金(61170037)

The National Natural Science Foundation of China (61170037)

臧鴻雁： 女，1973年生，副教授，研究方向為非線性系統同步理論與混沌密碼學.

黃慧芳： 女，1991年生，助教，研究方向為混沌密碼學.