數值模擬油氣管線彎管處固液兩相流場特性及沖刷腐蝕預測

, ,

(1. 中國石油西南油氣田公司 川西北氣礦，江油 621741； 2. 四川大學 建筑與環境學院，成都 610065)

數值模擬油氣管線彎管處固液兩相流場特性及沖刷腐蝕預測

杜強1,李洋2,曾祥國2

(1.中國石油西南油氣田公司川西北氣礦，江油621741； 2.四川大學建筑與環境學院，成都610065)

為了定量描述輸油管線彎管處由于流體方向改變引起的流場特性變化和管道內部沖蝕損傷過程，在Workbench平臺下利用Fluent建立了90°彎管沖蝕物理模型，獲得了彎管管壁壓力、剪切應力以及流體流速的分布規律。結果表明：彎管處流場變化復雜,是此處管道嚴重沖刷腐蝕的原因；彎管外側沖刷腐蝕最為嚴重，出口直管段的沖刷腐蝕次之，入口直管段及彎管內側幾乎無沖刷腐蝕；較大直徑的砂粒會攜帶更大的動能和沖擊力，從而在管壁上形成更加嚴重的沖刷腐蝕。

固體顆粒；數值模擬；沖刷腐蝕速率

Abstract： In order to quantitatively describe the changes of flow field characteristics and the internal erosion corrosion damage process due to the change of fluid direction in bends of pipelines, an erosion physical model of 90° elbow pipe was established under the Workbench platform, from which the distribution rules of pipe wall pressure, shear stress and fluid velocity in the elbow were obtained. The results show that the flow field in the elbow was complex, resulting in severe erosion corrosion in this place. The erosion corrosion of the outside of the elbow was most serious, followed by the straight section near outlet. There was almost no erosion corrosion on the inlet straight pipe and the inner side of the elbow. Larger diameter sands carried more kinetic energy and impact force, resulting in severer erosion corrosion on the tube wall.

Keywords： solid particle; numerical simulation; erosion corrosion rate

在石油和天然氣的開采過程中常伴隨著大量雜質的產生，其中腐蝕介質和固體顆粒會對輸送管道及工業設備產生腐蝕和磨損。目前，液固兩相流中固體顆粒對設備表面的沖刷腐蝕是一個重大的問題[1]。如固體顆粒對管壁的反復沖擊會使其過早的失效和損壞，導致油氣泄漏，這不僅會給企業帶來巨大的經濟損失，還有可能對人員安全造成威脅并對環境造成嚴重的危害。因此，準確描述液固兩相流流場特性、預測固體顆粒沖蝕位置和速率是防止管道和設備失效的有效方法。參考該方法優化設備的結構設計，對減少固體顆粒的沖刷腐蝕并延長設備的使用壽命有著重要的意義。

LIN等[2]利用計算流體動力學(CFD)預測了壓力堆核發電廠管線的水動力學特性和腐蝕速率。在核發電廠中，由于彎管處介質的流動特性，其腐蝕速率一般比直管處的高。其研究結果表明，二次流、分離區域、流體流速、壁面靜態壓力以及剪切應力都會影響彎管處的腐蝕行為。TILLY[3]的研究結果表明：當粒子直徑超過100 μm后，管壁的腐蝕速率幾乎不隨顆粒直徑變化。GANDHI等[4]通過研究砂粒尺寸對鑄鐵腐蝕的影響發現，砂粒粒徑與腐蝕速率之間呈線性關系。DESALE等[5]提出了腐蝕速率與顆粒尺寸之間呈指數關系。OKA等[6]提出的侵蝕率模型也闡述了顆粒尺寸對腐蝕速率的影響。本工作以90°彎管為研究對象進行數值模擬，得到在液固兩相流作用下流體流速、壁面壓力和剪切應力的分布規律及其與沖刷腐蝕間的聯系；利用模擬得到的顆粒尺寸與沖刷腐蝕速率間的關系，預測油氣管道沖刷腐蝕行為，并通過對比文獻中的相關試驗結果，驗證預測結果的有效性和正確性，為油氣管道沖刷腐蝕防護提供一定的指導意義。

1 固液兩相流沖蝕基本控制方程

以90°彎管為研究對象，液相為水，固相為砂粒。液固兩相流采用的流體力學基本方程[7]見式(1)～(6)。

流體運動方程：

流體動量方程：

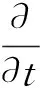
砂粒運動方程：

(3)

相對雷諾數為

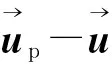
(5)

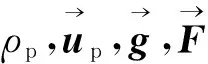
1.1 沖刷腐蝕理論模型

沖刷腐蝕模型為顆粒磨蝕與沉積(Particle Erosion and Accretion)模型[8]。該理論認為對于給定的材料，其沖刷腐蝕速率與流體速度、顆粒沖擊角度以及顆粒形狀函數相關。壁面的沖刷腐蝕速率R為

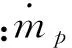
2 數值模擬

2.1 物理模型

模型采用的90°彎管管徑為100 mm，彎頭曲率半徑為100 mm，其幾何模型見圖1，管道材料為20鋼，流體為水。

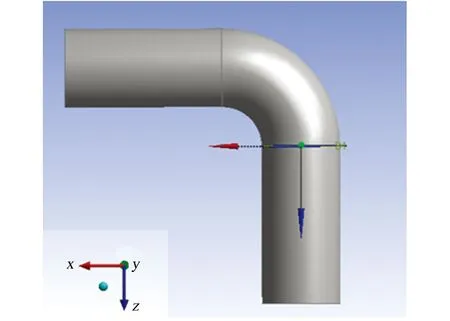
圖1 彎管幾何模型Fig. 1 Geometry model of elbow pipe

2.2 網格劃分及計算模型

采用fluent軟件中三維六面體網格對模型進行劃分，如圖2所示。該模型劃分的節點數為123 480，網格單元數為1 178 010，網格質量參數skewness值介于0.01～0.49。

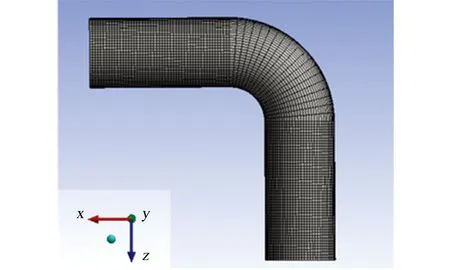
圖2 模型網格劃分Fig. 2 Mesh of the model

液相計算模型選擇標準 模型，砂粒(離散相)運動采用拉格朗日軌道模型，壓力-速度耦合采用SIMPLE方法，擴散項采用二階迎風差分方法。

流體入口邊界設置采用速度入口，流速為10 m/s；出口邊界條件設置為出流邊界條件(outflow)，對于不可壓縮流體，它是比較理想的出口邊界設置方式。

2.3 模擬結果與討論

2.3.1 管壁壓力

圖3(a)是管壁靜態壓力系數云圖，圖3(b)為管道截面不同圓心角φ處管壁靜態壓力系數沿著彎頭轉角(彎管段上某點與水平方向的夾角θ)的變化曲線。管壁靜態壓力系數Cp可以表示管壁壓力的大小，其定義式[2]為

式中：p為靜壓力；pr為參考壓力(即為大氣壓)；ρ流體密度；ub為流體平均流速，取9.863 m/s。

由圖3可見：當流體經過彎頭時，由于彎頭曲率和離心力的影響，從彎管內側到彎管外側，即φ從0°增大至180°時，流體對管壁的壓力呈現出逐級增大的趨勢；彎管內側壓力隨著θ的變化先減小后增加，外側壓力變化趨勢與之相反。

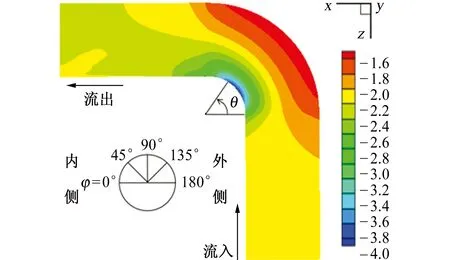
(a) 管壁靜態壓力系數云圖

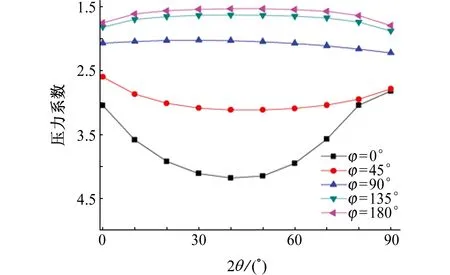
(b)不同φ處壓力系數隨θ的變化曲線圖3 管壁壓力系數的模擬結果Fig. 3 Simulated results of wall pressure coefficient: (a) static pressure coefficient contour of pipe wall;(b) variation curves of pressure coefficient with θ at different φ

2.3.2 流體流速

圖4是xoz平面內流體流速。從圖4并結合圖3可以看出：在彎管段，流體對管道的壓力和流體流速均取得最值，并且在此部位變化最為劇烈。這說明相對于直管段，彎管段更容易發生破壞。在彎管段壓力最大的外側，對應的流體流速卻很小，而壓力最小的內側，流體流速最大；因為當流體流入彎頭時，彎管曲率會使流體沿截面方向產生較大的離心力，在離心力的作用下，對彎管外側管壁產生擠壓應力，而對彎管內側管壁形成牽引作用[9]。根據伯努利方程，同一流線上各點處單位質量流體所具有的總能量為常數。壓力沿著離心力方向逐漸增大，為保持總能量不變，動能必然沿著離心力方向逐漸減少，故流體硫酸相應減小，反之亦然。

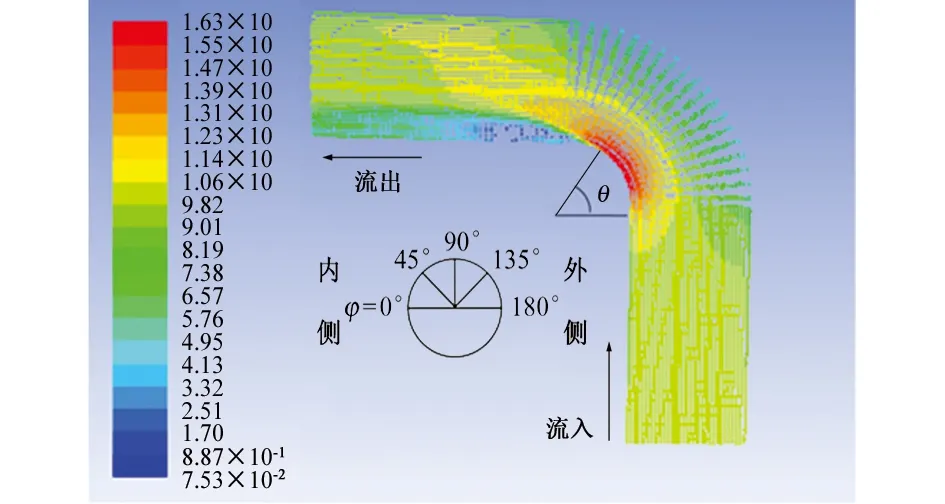
(a) 流體流速云圖

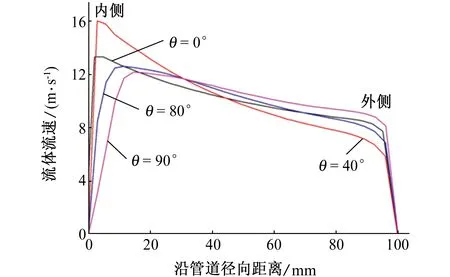
(b) 不同θ角處流體流速沿管道徑向的變化曲線圖4 xoz平面內流體流速的模擬結果Fig. 4 Simulated results of fluid velocity in xoz plane:(a) flow velocity contour of fluid；(b) curves of fluid velocity along the radial direction of pipeline at different angles of θ

由圖4還可見：在θ=0°時，由于曲率和離心力作用，彎管內側流體開始加速，外側流體流速開始降低。θ=40°時，流體流速達到最大，在二次流的作用下，彎管內側高速流體會向管道中心流動，而外側流體向彎管內側流動。此時，內側壓力開始逐漸增大，外側壓力變化趨勢相反，彎管段流場復雜，增加了該處沖刷腐蝕的可能性。從邊界層的角度來看，此時邊界層厚度開始增加。當θ在80～90°時，流體流速沿管道徑向的變化趨勢基本相同，兩者之間的差值較小。

2.3.3 壁面摩擦因數

壁面摩擦因數反映了流體對管壁作用的剪切應力的分布規律，壁面摩擦因數定義式[2]為

式中：τw為壁面剪切應力。

由圖5可見：在彎管內側(φ=0°)，當θ≤40°時，壁面摩擦因數隨著θ角的增大而逐漸增大，因為彎管曲率和離心力的作用使管壁附近的流體加速，速度梯度增大，而流體對壁面剪切應力與速度梯度成正比，因此剪切應力逐漸增大；當θ>40°時，彎管內側管壁壓力逐漸增大，這意味著流體的動能和流速減小，從而使壁面摩擦因數逐級減小；當θ=90°時，彎管內側壁面摩擦因數減小至一個很小的值，這主要因為與流體流速成反比的邊界層厚度增加，相應地流體流速降低。在離彎管內側較近處(φ=45°)，摩擦因素隨θ的變化趨勢與φ=0°時類似。同時,由于二次流和離心力的影響，彎管內側具有較大流速的流體流向外側，從而引起外側壁面摩擦因數在θ為40°時開始增大。在離彎管外側較近處(φ=135°)，摩擦因素曲線與φ=180°時趨勢相同；管道中部流體流速波動不劇烈，因此φ=90°時曲線變化幅度較小。

2.3.4 管壁沖刷腐蝕

由圖6可見：彎管外側管壁的沖刷腐蝕最為嚴重，此處管壁的腐蝕深度最深，沖刷腐蝕速率達到18 mm/a，并且沖刷腐蝕面積分布最廣；出口直管段的沖刷腐蝕次之，而入口直管段和彎管內側幾乎沒有發生沖刷腐蝕。因為在入口直管部分，流體攜帶著砂粒平行于管壁流運動，砂粒很難與壁面發生碰撞，但是流體的湍流波動會改變砂粒的運動路徑，使之與管壁發生碰撞，造成了此部分產生十分輕微的沖刷腐蝕。由于彎管曲率和離心力的作用，砂粒隨著流體流向彎管外側，降低了與內側管壁碰撞的概率，因此也減小了內側管壁沖刷腐蝕的可能性。在θ=90°處，出口直管段內側也沒有發生沖刷腐蝕。一方面，此處流體流速很低，增大了邊界層的厚度，而砂粒需要穿過壁面附近的流體，才能與管壁發生碰撞，較大的邊界層會使砂粒碰撞速率大大減小甚至沒法到達壁面；另一方面，砂粒與彎管外側發生碰撞后會反彈向內側管壁運動，而此區域正好處于反彈砂粒很難到達的位置。因此這部分管壁的腐蝕不嚴重。同時，這也是這部分區域周圍腐蝕較為嚴重的原因。彎管外側、θ為40～90°處的管壁為沖刷腐蝕最為嚴重的區域。這主要是因為從入口流入的流體會與該區域產生直接接觸，使其攜帶的砂粒與壁面發生碰撞，砂粒撞擊壁面會形成淺坑并在其周圍產生片狀物，而這些片狀物很容易被后續的撞擊砂粒從壁面上分離出去[10]，從而導致管壁腐蝕。此外，該區域存在湍流強度增大以及二次流，這加大了流場的復雜性，增大了砂粒與壁面碰撞的概率，從而使此區域沖刷腐蝕最為嚴重。

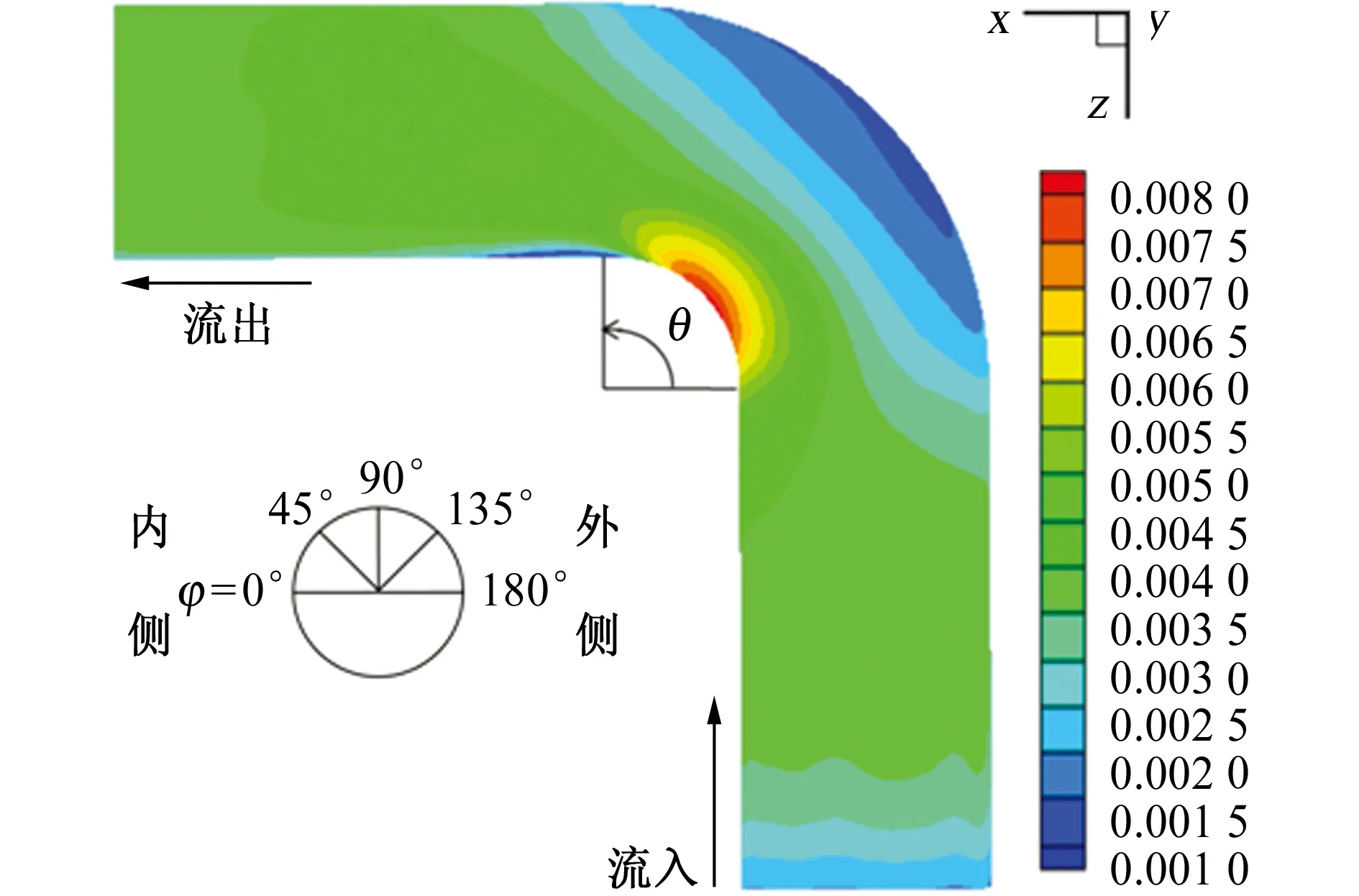
(a) 壁面摩擦因數云圖

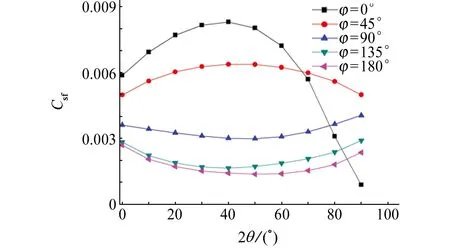
(b) 不同φ處的壁面摩擦因數隨θ的變化曲線圖5 彎管壁面摩擦因數的模擬結果Fig. 5 Simulated results of friction coefficient of elbow pipe wall： (a) friction factor contour of wall; (b) variation curves of wall fraction factor with θ at different φ

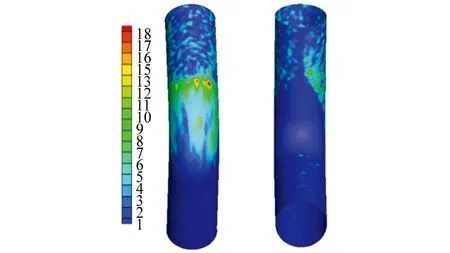
(a) 彎管內沖刷腐蝕速率分布(mm/a)

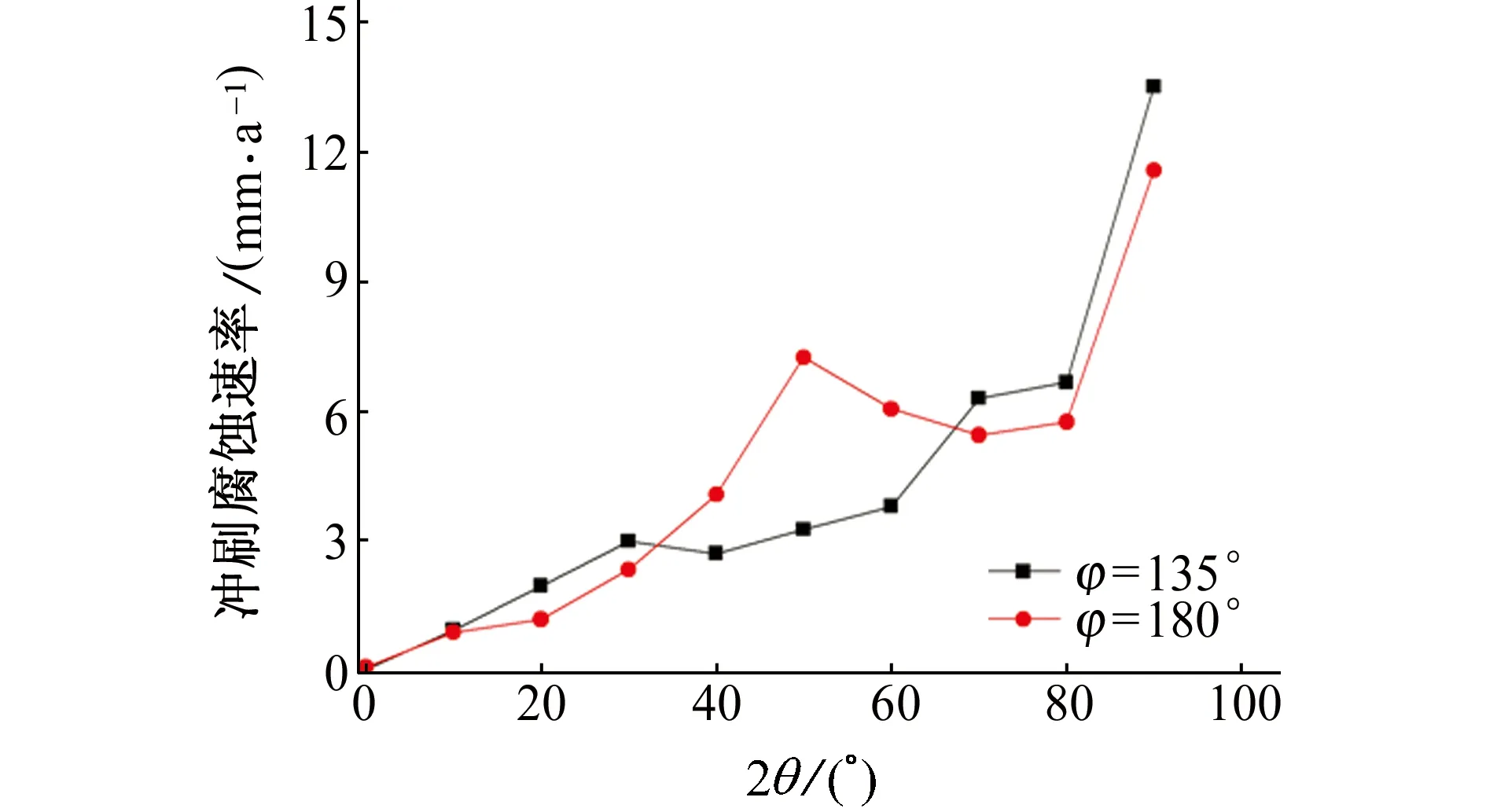
(b) 不同φ處沖刷腐蝕速率隨θ的變化曲線圖6 彎管管壁沖刷腐蝕速率的模擬結果Fig. 6 Simulated results of erosion corrosion rate of elbow pipe wall： (a) corrosion rate distribution of erosion corrosion in inner elbow pipe (mm/a); (b) variation curves of erosion corrosion rate with θ at different φ

2.3.5 砂粒直徑與管壁沖蝕速率的關系

在其他條件不變情況下，將砂粒直徑分別設置為0.1，0.2，0.4，0.6，0.8，1.0 mm，模擬了砂粒直徑與管壁沖蝕速率的關系。為了減小誤差，每種砂粒直徑進行兩次數值模擬。

圖7為不同砂粒直徑與管壁沖蝕速率間的關系曲線，通過一系列的曲線擬合發現線性擬合的相關系數最為接近于1，故二者之間近似滿足線性變化關系，這與文獻[4-5]的結論一致。

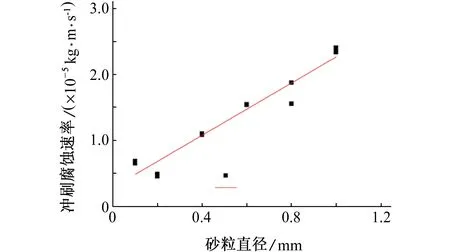
圖7 沖刷腐蝕速率與砂粒直徑間的關系Fig. 7 The relationship between the particle diameter and the wall corrosion rate

由圖7可見，壁面沖刷腐蝕速率隨著砂粒直徑的增大而增大。固體顆粒尺寸會影響砂粒撞擊速率和動能[11]。與小直徑的砂粒比較，大直徑砂粒數量較少，但其擁有更大的動能和沖擊力，在撞擊速率、形狀、密度和硬度相同的情況下，大直徑砂粒對壁面的沖擊力作用更大，造成的腐蝕也更嚴重。同時，小尺寸砂粒易于被流體流動所影響，也更容易與流體產生動量交換，它們在穿過黏性層時會損失更多的動量，甚至被黏性層捕獲而無法沖擊壁面，所以小尺寸砂粒對壁面產生的沖刷腐蝕較輕。

3 結論

(1) 從彎管內側到彎管外側，即φ從0°增大至180°時，流體對管壁的壓力呈現出逐級增大的趨勢。彎管內側壓力隨著θ的變化先減小后增加，外側壓力變化趨勢與之相反。彎管處流場變化復雜，與此處管道腐蝕的嚴重性相互映證。

(2) 彎管外側壓力大而流體流速小，彎管內側壓力小流速大。彎管段流場復雜，流體流速波動最為劇烈。

(3) 彎管外側沖刷腐蝕最為嚴重，出口直管段的沖刷腐蝕次之，入口直管段及彎管內側幾乎無腐蝕。

(4) 對于20鋼，在其他條件相同的情況下，較大直徑的砂粒會攜帶更大的動能和沖擊力，從而在管壁上形成更加嚴重的沖刷腐蝕。

[1] 梁穎,袁宗明,陳學敏,等. 基于CFD的液固兩相流沖刷腐蝕預測研究[J]. 石油化工應用,2014,33(2):103-106.

[2] LIN C H,FERNG Y M. Predictions of hydrodynamic characteristics and corrosion rates using CFD in the piping systems of pressurized-water reactor power plant[J]. Annals of Nuclear Energy,2014,65:214-222.

[3] TILLY G P. A two stage mechanism of ductile erosion[J]. Wear,1973,23(1):87-96.

[4] GANDHI B K,BORSE S V. Effects of particle size and size distribution on estimating erosion wear of cast iron in sand-water slurries[J]. Indian Journal of Engineering & Materials Sciences,2002,9(6):480-486.

[5] DESALE G R,GANDHI B K,JAIN S C. Particle size effects on the slurry erosion of aluminium alloy (AA 6063)[J]. Wear,2009,266(11):1066-1071.

[6] OKA Y I,OKAMURA K,YOSHIDA T. Practical estimation of erosion damage caused by solid particle impact[J]. Wear,2005,259(1):95-101.

[7] 吳克啟,舒朝暉. 高等流體力學[M]. 北京:中國電力出版社,2009.

[8] N?KLEBERG L,S?NTVEDT T. Erosion of oil & gas industry choke valves using computational fluid dynamics and experiment[J]. International Journal of Heat and Fluid Flow,1998,19(6):636-643.

[9] 梁光川,聶暢,劉奇,等. 基于FLUENT的輸油管道彎頭沖蝕分析[J]. 腐蝕與防護,2013,34(9):822-824.

[10] BELLMAN R,LEVY A. Erosion mechanism in ductile metals[J]. Wear,1981,70(1):1-27.

[11] PARSI M,NAJMI K,NAJAFIFARD F,et al. A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications[J]. Journal of Natural Gas Science and Engineering,2014,21:850-873.

Prediction of Flow Field Characteristics of Solid-Liquid Phases and Erosion Corrosion in Elbows of Oil-Gas Pipelines Using Numerical Simulation

DU Qiang1, LI Yang2, ZENG Xiangguo2

(1. Northwest Sichuan Gasfield, Petrochina Southwest Oil and Gasfield Company, Jiangyou 621741, China;2. College of Architecture and Environment, Sichuan University, Chengdu 610065, China)

10.11973/fsyfh-201710003

TG172

A

1005-748X(2017)10-0751-05

2016-01-23

李 洋(1992-),碩士研究生，主要從事結構力學方向的研究,15828036142，775621002@qq.com