初中生數學學習策略調查問卷的設計與編制

王光明，劉 丹

?

初中生數學學習策略調查問卷的設計與編制

王光明，劉 丹

（天津師范大學教師教育學院，天津 300387）

通過查閱文獻資料與已有成熟問卷，征詢專家意見，將初中生數學學習策略劃分為三大維度：認知策略、元認知策略、資源管理策略，并確立了10個子維度的操作性定義．根據操作性定義，結合已有問卷，形成原始問卷．通過4次數據收集，經過多次項目分析、驗證性因素分析、探索性因素分析，對問卷題目進行相應刪減、增添、修改，最終形成“初中生數學學習策略調查問卷”．該問卷信效度指標良好，可作為測量初中生數學學習策略水平的有效工具．

初中；數學學習策略；問卷編制；量表

1 引 言

教育界將“教會學生學習，使學生掌握有效的學習策略”視為提高學習質量，減輕學習負擔，大面積提高教學質量的有效措施．關于學習策略的研究，經歷了從通用的學習策略到學科學習策略的發展過程，其中數學學習策略的研究受到了一定關注[1]．數學學習策略是高效率數學學習學生心理結構的重要組成部分[2]，有效的數學學習策略能夠顯著提高學生的數學學業水平，改善數學學習的態度和情感，對各學段學生的數學學習都存在積極影響[3~7]．數學學習策略對數學學習有著重要的作用，如何測量和評價學生的數學學習策略水平是相關量化研究中的重要環節．然而，目前針對中國初中生數學學習策略的測評工具尚十分罕見，研制科學規范的初中生數學學習策略調查問卷，成為亟待解決的問題．研究將參考已有數學學習策略問卷和量表，以初中生為研究對象，編制相應的數學學習策略調查問卷，為初中生數學學習策略特征的調查與量化研究提供有效的工具．

2 相關研究述評

2.1 數學學習策略成分的理論框架

學界對學習策略概念的界定眾說紛紜，進而對學習策略結構的看法也不盡相同．具有代表性的分類有以下幾種．

丹瑟路（Dansereau）根據學習策略所起的作用，將學習策略分為基礎策略和支持策略兩類．基礎策略是指直接操作材料的各種學習策略，主要包括信息的獲得、貯存，信息的檢索和應用的策略，如識記、組織和回憶等策略．支持策略主要指幫助學習者維持適當的學習心理狀態，以保證基礎策略有效操作的策略，如集中注意策略、自我監控和診斷策略[8]．溫斯坦（Weinstein）認為學習策略包括認知信息加工策略，如精加工策略等；積極學習策略，如應試策略等；輔助性策略，如處理焦慮的策略；元認知策略，如監控新信息的獲得策略[9]．邁克卡（Mckeachie）等人根據學習策略覆蓋的成分，將其概括為認知策略、元認知策略、資源管理策略．認知策略包含復述策略、精加工策略和組織策略；元認知策略包含計劃策略、監控策略、調節策略；資源管理策略包含時間管理策略、學習環境管理策略、努力管理和其他人的支持[10]．

參考國外的學習策略調查問卷，中國研究者也編制了一系列數學學習策略調查問卷．譬如，劉電芝編制的“小學生數學學習策略量表”，該量表包含兩個主要維度，數學元認知策略（計劃策略、監控調節策略、評價反思策略、策略意識）與數學認知策略（數學概念策略、計算學習策略、解應用題策略、幾何知識學習策略）[11]．姚志敏編制的“中學生數學學習策略量表”，包含數學元認知策略、認知策略、資源管理策略和情感策略4個維度[12]．王光明編制的“高中生數學學習策略調查問卷”，將數學學習策略劃分為數學認知策略、數學元認知策略和數學資源管理策略[13]．

國外研究者對于學習策略的結構劃分，具有一定的相似性．丹瑟路和溫斯坦對學習策略結構的劃分，多數可歸類到認知策略、元認知策略和資源管理策略中，即邁克卡等人關于學習策略的分類．國內研究者在進行數學學習策略的維度分類時，也基本符合這一觀點，分為數學認知策略、數學元認知策略和數學資源管理策略3類[14]．

2.2 數學學習策略問卷的相關研究

學習策略研究的基本問題之一，在于如何編制有效調查工具測評學生的學習策略水平．已有的各類學習策略調查問卷各有其優勢所在，但也有不足．如溫斯坦等人編制的“學習策略量表”（，）[15]，該量表最初為大學版，后改編為高中版；美國密執安大學賓特利奇（Pintrich）等人編制的學習動機與策略問卷（，）[16]，包含動機和學習策略兩部分，該量表有大學版和中學版，盡管這兩個版本的學習策略調查問卷都不涉及具體學科，但卻都被研究者直接用于測驗學生在數學學習中的策略使用情況．

目前已有的一些學習策略測量工具，鮮有專門針對初中生而設計，與數學學科的結合也并不緊密，甚至部分測量工具的編制過程也不夠嚴謹．具體表現為兩大類問題：第一，問卷的編寫表述不明確，包括指導語表述不明確，以及測試題目表述不明確．第二，通過各類指標參數修訂問卷的過程不規范．針對第一類問題，編寫指導語時應明確題目中各個選項的定義，如在李克特量表中，就應清晰地告知作答者各等級選項的具體標準，盡可能地保證測驗的科學性．測試題目表述不明確，主要包括程度副詞的使用，以及模棱兩可的詞匯．譬如，測試題目“數學考試之前，我通常會根據自己的實際情況，有針對地復習一下”中，不同作答者對于“通常”的理解便可能存在偏差，應盡量避免使用此類語言．針對第二類問題，在問卷試題修訂過程中，利用統計軟件運算得到的各參數指標可以作為刪減題目的依據，但不能將其作為刪減題目的唯一依據，還需要考慮保留題目的語義是否清晰精簡、是否覆蓋所有維度等問題；進行因素分析時，探索性因素分析和驗證性因素分析要使用不同的樣本，進行驗證性因素分析時要注意在分析過程中重新取樣的問題．

3 問卷編制過程與方法

3.1 問卷維度及其操作性定義的確定

“初中生數學學習策略調查問卷”的維度確定主要包含兩個步驟：（1）查閱文獻資料與已有成熟問卷，擬定問卷維度及其操作性定義；（2）征詢專家意見，確定問卷維度及其操作性定義．

首先，通過查閱梳理文獻，以及已有的國內外成熟（數學）學習策略問卷，擬將初中生數學學習策略劃分為三大維度（數學認知策略、數學元認知策略和數學資源管理策略），并編寫各子維度的操作性定義．

其次，于2016年3—9月期間，分別對多位知名專家學者進行訪談，包括北京師范大學曹一鳴教授，南京師范大學喻平教授，天津師范大學李洪玉教授，佛羅里達海灣大學張京順博士等，訪談內容包括問卷維度的具體劃分及子維度操作性定義的具體界定．

綜合文獻資料、已有成熟問卷或量表，以及專家意見，最終確定問卷的維度，其中包括3個主維度，10個子維度．數學學習策略的維度劃分見圖1，各子維度的操作性定義見表1．

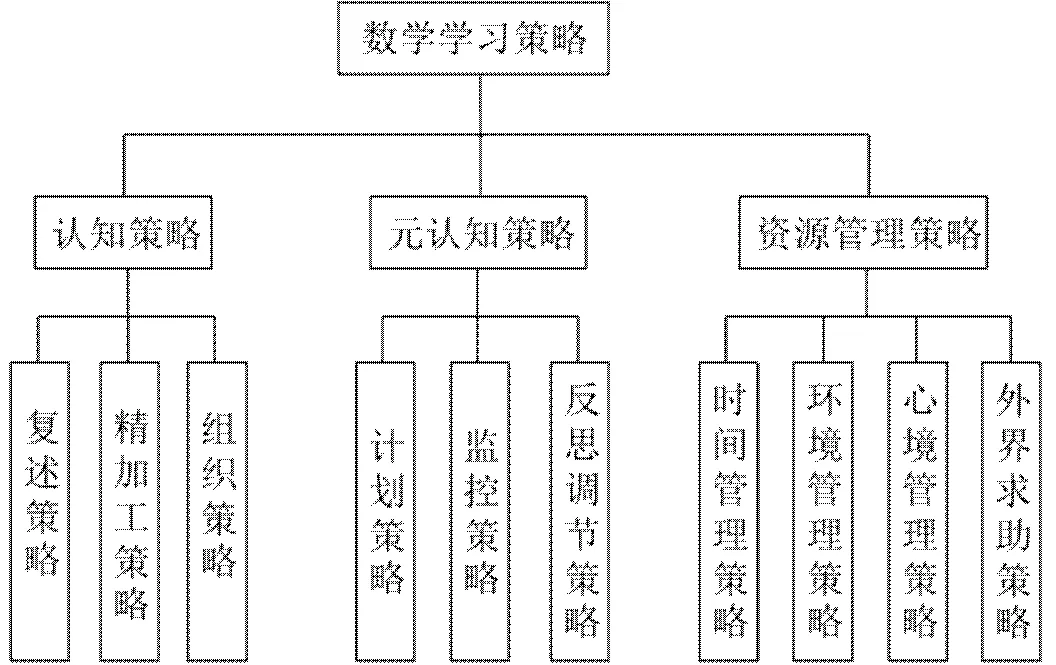
圖1 數學學習策略的維度劃分

表1 數學學習策略子維度的操作性定義

3.2 問卷題目的建立

所編初始問卷的題目主要來自于：（1）溫斯坦的“學習策略問卷”（LASSI）[15]；（2）王光明的“高中生數學學習策略調查問卷”[13]；（3）莫秀鋒的“數學學習策略量表”[1]．

考慮中國初中生數學學習的特點，引用和改編上述問卷的題目內容，建立了87道題目的問卷，其中認知策略26道，元認知策略28道，資源管理策略27道，測謊題6道．問卷采用likert五點法計分，將題目選項中的“非常符合”、“符合”、“不確定”、“不符合”、“非常不符合”分別計分為“5”、“4”、“3”、“2”、“1”．采用隨機法編排題目順序．

3.3 被試選取與問卷回收

問卷編制過程中，采用整群抽樣法共進行4次測試．對于每次測試回收的問卷，通過以下兩個步驟剔除無效問卷．第一步：目測，剔除問卷答案呈現規律性、周期性、統一性的無效問卷；第二步：根據測謊題對剩余的問卷繼續進行篩選，凡是對測謊題回答差異性過大的均作為無效問卷剔除．

首次測試調查對象為預測試樣本．包括天津市的4所典型學校共8個班級的學生，分別是實驗中學、方舟實驗中學、海河中學、天津五中的七年級和八年級學生．總共發放問卷330份，回收286份，通過兩步問卷篩選，最終得到有效問卷209份．

第二次所測樣本，主要用于問卷研制過程中的探索性因子分析．調查對象來自天津、湖北、遼寧、甘肅、江蘇的5所中學．總共發放問卷610份，回收552份問卷，通過兩步問卷篩選，最終得到有效問卷428份．

第三次所測樣本，主要用于問卷研制過程中的驗證性因子分析．調查對象來自天津、山東、廣州的3所學校．總共發放問卷300份，回收264份問卷，通過兩步問卷篩選，最終得到有效問卷209份．

第四次所測樣本，主要用于計算問卷的重測信度．選取了參與過第二次測試的兩所中學學生．共發放問卷160份，回收問卷142份，通過兩步問卷篩選，最終得到有效問卷113份．

3.4 數據分析工具

利用SPSS18.0和AMOS21.0軟件處理和分析問卷各參數指標．

4 問卷的預研究結果與分析

4.1 項目分析

對反向計分題進行反向計分后，按兩個步驟對問卷的81道題目（不包括測謊題目）進行項目分析：首先，利用題總相關法對首次測試中所有被試的各題目得分與整卷總得分進行相關分析．一般情況下，當Pearson積差相關系數值低于0.4時，可認為二者之間存在低度相關．在0.05的顯著性水平下，共計刪除各題項得分與總分的Pearson積差相關系數低于0.4的題目13道．其次，采用臨界比率法（Critical Ratio）進行高低分組的差異顯著性進行檢驗，將數學學習策略得分按升序排序，前27%為低分組，后27%為高分組，對兩組進行獨立樣本檢驗，刪除不具有高低分組顯著性差異的題目．結果顯示，通過題總相關法刪除題目后，剩余題目均滿足高低分組間的差異顯著性．經過項目分析，最終得到道68題目（不包括測謊題）．

4.2 探索性因素分析

將修訂后的問卷進行第二次測試，利用所得數據先后對問卷整體以及3個主維度進行探索性因素分析．4次探索性因素分析前，所進行的檢驗值均達到0.9以上，Bartlett球形檢驗相關性顯著（），說明樣本數據適合進行探索性因素分析．

在SPSS軟件中使用主成分分析以及最大方差旋轉法確定問卷因子數及題目．保留問卷中的題目遵循如下原則：（1）因子特征值大于1；（2）因子載荷值至少在0.4以上；（3）在不同因子上載荷量不能均大于0.4；（4）提取出的主成分符合陡階檢驗；（5）每個因子至少包含3道題目；（6）一次只刪除一道題目，每一次刪除題目之后用新的數據重新檢驗和分析．因子命名的原則如下：（1）如果某個因子的題目主要來自數學學習策略模型的某個子維度，則以該子維度命名；（2）如果對某個因子方差貢獻率一半以上的題目分散來自于數學學習策略模型的不同子維度，則參考這些題目的共同數學學習策略進行命名．

通過探索性因素分析，共刪除18道題目，保留了“數學學習策略調查問卷（第一版）”中的37道題目．盡管各類指標可以作為篩選題目的依據，但是不能僅依靠指標篩選題目，還需要考慮保留題目的語義是否清晰精簡、維度劃分的實際意義、因題量過多導致學生的作答專注度不高等問題．考慮到上述原因，需要對原維度進行合并或拆分，并重新命名．又結合學生答題過程中對第一版問卷中的部分題目的反饋，對部分題目的表述方式進行了修訂．再將題目交叉混合編排，得到修改后的第二版問卷，共含46道題目（包括42道正式題目和4道測謊題），其中認知策略采用三因素結構，復述策略共5題，精加工策略共4題，組織策略共5題；元認知策略采用三因素結構，計劃策略共6題，監控策略共6題，反思調節策略共4題；資源管理策略采用四因素結構，時間管理策略共3題，環境管理策略共3題，心境管理策略共3題，外界求助策略共3題．

5 問卷的正式確定及結果分析

為進一步修訂和完善數學學習策略問卷，對第二次與第三次所測的樣本進行再測問卷的調查．對回收問卷數據進行處理，通過項目分析和因素分析，對問卷的理論調查模型進行檢驗和調整．

5.1 項目分析與探索性因素分析

使用第二版問卷對第二次調查樣本進行分析．先進行高低分組顯著性差異的檢驗和題總相關性的分析后，刪除第15題和第17題，剩余44道題目．再對數據進行探索因素分析，結果表明問卷因子確定合理，與理論框架基本吻合，進而確定第三版問卷．

5.2 驗證性因素分析

使用第三版問卷對第三次測試樣本進行調查，利用AMOS 21.0軟件對數據進行驗證性因素分析，以此檢驗實際測量結果與理論模型擬合效果是否良好．在對二階3因子模型進行擬合前，先建立一階10因子模型，再次篩選題項．通過分析一階10因子模型的各主要參數指標，刪除因子載荷值小于0.5的題目（第4、5、10、12、31、34題），剩余34道題．其次，通過觀察修正指數，發現有兩對題目之間的值在20以上，表明題目之間的相關性過高，刪除第6、33題．

5.3 問卷的信度和效度指標

5.3.1 信度分析

信度是指測試結果的一致性、穩定性和可靠性，信度系數愈高，表示測試的結果愈一致、穩定和可靠．通過計算問卷的內部一致性和重測信度分析問卷的信度．數據分析結果（見表3）表明，初中生數學學習策略調查問卷的各主維度Cronbach’s系數在0.839~0.888之間，Spearman-Brown分半信度在0.768~0.856之間，說明編制的數學學習策略調查問卷各主維度內部題目的一致性程度很高．總問卷的Cronbach’s系數為0.970，Spearman-Brown分半信度為0.937，表明編制的數學學習策略調查問卷具有較好的內部一致性．重測時選取第四次測試樣本，采用Pearson積差相關系數作為問卷的重測信度，分析兩次測試分數的相關性．結果表明，問卷各主維度的重測信度在0.858~0.891之間，總問卷的重測信度為0.906．由此可知，問卷具有很好的內部一致性．結合各項信度指標，認為“初中生數學學習策略調查問卷”信度較高．

表2 二階3因子模型擬合指數

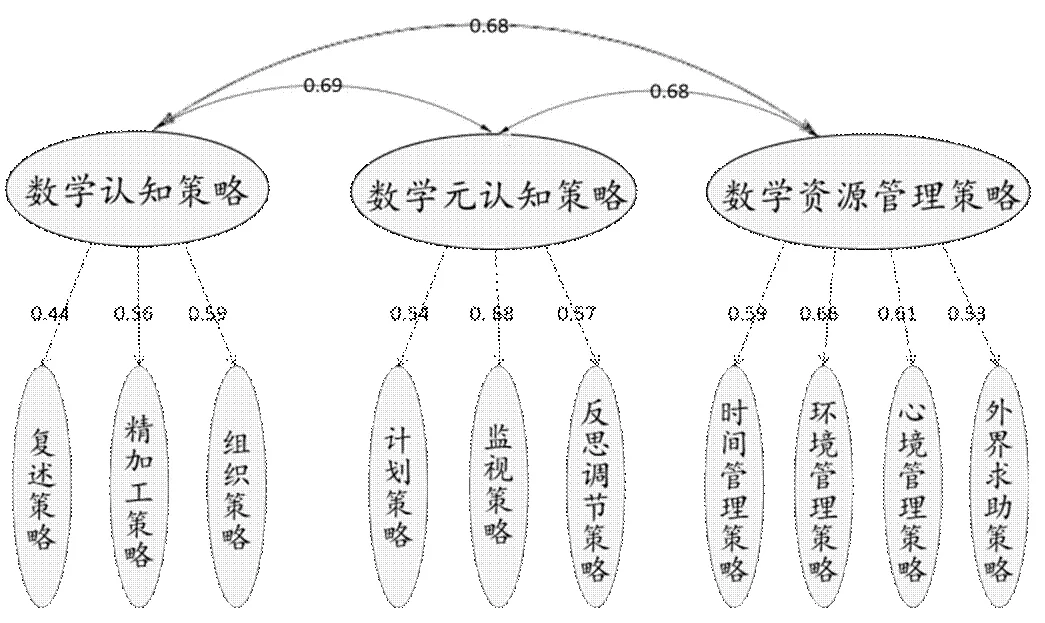
圖2 初中生數學學習策略結構路徑系數

表3 數學學習策略特征問卷信度

5.3.2 效度分析

效度即有效性，是指測量工具能夠測出所需測量的內容的程度，效度越高，說明測量結果與要考察的內容越吻合；反之，則二者吻合度越低．通過分析問卷的內容效度和結構效度，以考察所編制問卷對于初中生數學學習策略特征測量的有效性．

（1）內容效度．

內容效度是指問卷題目反應所要測量的內容能否達到測量目的的程度．在形成初測問卷之前，題目內容借鑒了國內外已有量表或問卷，并考慮中國初中生數學學習的實際情況；之后又曾與多位專家進行討論，討論包括問卷的指導語編寫、問卷的結構和題目編寫的注意事項等內容，根據專家的意見對問卷中存在問題的題目進行修改或刪除，構建調查模型，確定“初中生數學學習策略調查問卷”的題目．

在最終版本問卷內容效度的評價階段，邀請了北京師范大學曹一鳴教授、南京師范大學喻平教授、天津師范大學李洪玉教授和王曉莊教授4位心理學或數學教育領域的專家，對問卷中每一題目與其所屬維度的相關性做出評價，根據專家評價結果計算問卷的內容效度．結果表明，4位評價者間的一致性水平為0.84，表明評價者間具有較好的一致性．問卷條目水平的內容效度指數見表4．

表4 內容效度指標

（2）結構效度．

以驗證性因素分析所顯示的二階模型擬合指標作為結構效度的指標之二．上文分析中，調查數據對模型的擬合已達到標準要求，認為“初中生數學學習策略調查問卷”的一階10因子二階3因子結構模型可以接受．

6 討 論

自制的“初中生數學學習策略調查問卷”與“高中生數學學習策略調查問卷”[13]的編制過程既有相同，也有不同之處．繼承了“高中生數學學習策略調查問卷”中對于數學學習策略維度的劃分，“初中生數學學習策略調查問卷”也將數學學習策略分為數學認知策略、數學元認知策略和數學資源管理策略3個維度．不同之處體現在以下3個方面．

（1）題目數量和內容．“初中生數學學習策略調查問卷”包含的題目數量少于“高中生數學學習策略調查問卷”中題目數量，問卷題目的內容符合初中生數學學習的特點．精簡問卷題目數量，避免學生由于答題時間過長而注意力分散，進而造成收集數據失真的情況，保證了所收集數據的真實性．

（2）題目和指導語的表述．“高中生數學學習策略調查問卷”題目表述中出現了“很少”、“常常”等這樣表示頻率的詞語，例如，“我很少在實際生活中用到所學習的數學知識”，“我常常總結一些代表性的例題和解題方法”，這樣的題目表述不是很清晰，易引起歧義．“初中生數學學習策略調查問卷”的編制過程中，為明確測試題目，題目的表達方式避免使用表示頻率的詞語，在指導語中增加了題目各個等級選項的定義．

（3）問卷的驗證性因素分析．運用因素分析修訂問卷的過程中，“高中生數學學習策略調查問卷”的驗證性因素分析和探索性因素分析使用了同一樣本數據，這種做法值得商榷．用于探索性因素分析時選用的樣本數據進行驗證性因素分析以支持自己的結論，這種“自圓其說”的做法是不可取的[17]．“初中生數學學習策略調查問卷”的編制過程中，為更好地檢驗問卷的各個題目與構想的理論模型是否具有良好的擬合效果，采用與探索性因素分析時不同的樣本數據進行驗證性因素分析．

問卷的編制，通過文獻的梳理，結合專家意見，初步建構了數學學習策略調查問卷模型，形成第一版問卷，經多次測試與修訂，分別得到第二、三、四版問卷．在四版測試數據的基礎上，對調查模型進行修訂，確立調查問卷的結構模型．“初中生數學學習策略水平調查問卷”共包含36道題目，分為3個維度和測謊題構成，具體題目分布見表5．

“初中生數學學習策略調查問卷”具有較好的信度和效度．該問卷具有扎實的理論基礎，合理的結構框架．但由于各方面的限制，問卷的編制尚未制定全國常模，這是進一步研究的方向．

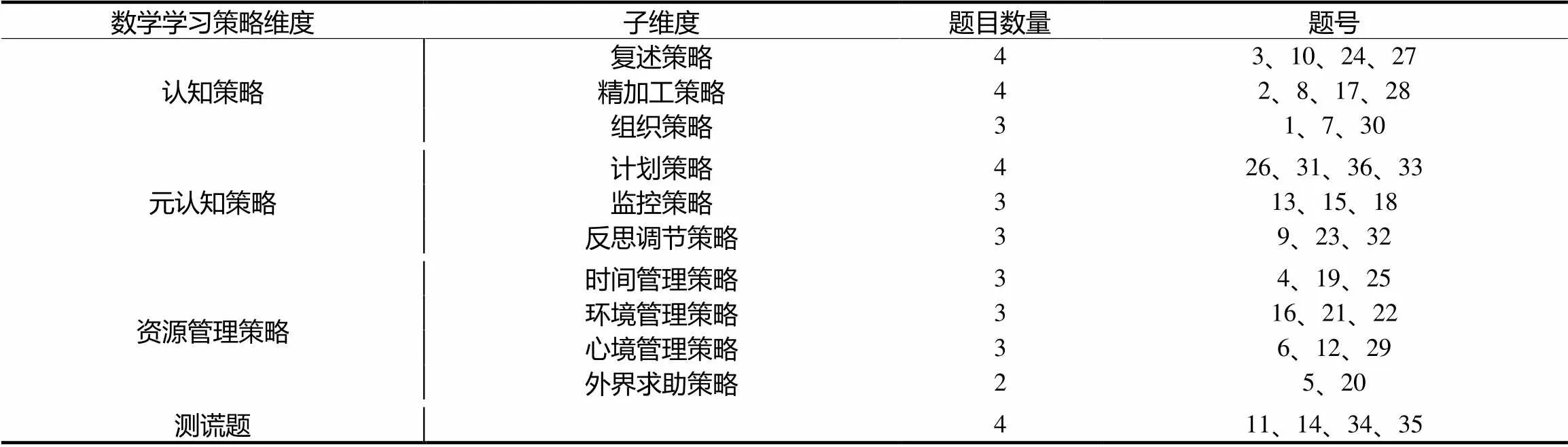
表5 初中生數學學習策略水平調查問卷題目安排（第四版）

注：11題與34題，14題與35題為兩兩對應的測謊題

7 結 論

“初中生數學學習策略調查問卷”研制過程科學客觀，具有良好的信度和效度指標，可作為調查與評價初中生數學學習策略水平的有效工具．

[1] 莫秀鋒．初中生數學學習策略的發展特點及可控心理影響因素研究[D]．西南師范大學，2002．

[2] 王光明，佘文娟，宋金錦．基于NVivo10質性分析的高效數學學習心理結構模型[J]．心理與行為研究，2014，（1）：74-79．

[3] 康玥媛，張楠，王光明，等．基高效率數學學習高中生數學成績的影響路徑[J]．心理與行為研究，2016，（3）：352-359．

[4] 王桂云，沈自飛．關于高職生數學學習策略的研究與思考[J]．數學教育學報，2005，14（2）：97-99．

[5] 湯服成，梁宇．小學四~六年級學生數學元認知監控學習策略培養的研究[J]．數學教育學報，2008，17（1）：47-50．

[6] 莫秀鋒，劉電芝．初中生數學學習策略的個體差異研究[J]．數學教育學報，2007，16（4）：56-58．

[7] 劉電芝，高嵐，錢建國，等．小學生數學學習策略掌握現狀分析[J]．數學教育學報，2013，22（6）：27-31．

[8] Dansereau D F.[A]. In: Segal J W, Chipman S F, Glaser eds.[C]. Hillsdale NJ Erlbaum, 1985.

[9] 劉儒德．論學習策略的實質[J]．心理科學，1997，（2）：179-181．

[10] 陳琦，劉儒德．當代教育心理學[M]．北京：北京師范大學出版社，1997．

[11] 劉電芝．小學兒童數學學習策略的發展與加工機制研究[D]．西南師范大學，2003．

[12] 姚志敏．場獨立—場依存認知風格對初中生數學學習策略的影響研究[D]．江西師范大學，2008．

[13] 王光明，廖晶，黃倩，等．高中生數學學習策略調查問卷的編制[J]．數學教育學報，2015，24（5）：25-30．

[14] 廖晶，王光明，黃倩，等．高中生高效率數學學習策略特征及對數學學業水平的影響路徑[J]．數學教育學報，2016，25（5）：65-70．

[15] Weinstein C E, Palmer D R. Learning and Study Strategies Inventory (High School Version) [EB/OL]. http://www. hhpublishing.com/_assessments/LASSI/. H&H Publishing Company, Inc, 1990.

[16] Pintrich P R. A Manual for the Use of the Motivated Strategies for Learning Questionnaire (MSLQ) [EB/OL]. http://files.eric.ed.gov/fulltext/ED338122.pdf. The Regents of the University of Michigan, 1991.

[17] 劉軍，富萍萍．結構方程模型應用陷阱分析[J]．數理統計與管理，2007，（2）：268-272．

附錄：初中生數學學習策略調查問卷

親愛的同學：

你好！為了解初中生數學學習過程中的一些想法和感受，我們邀請你參與此次調查．感謝你的配合．此次調查具體要求如下：

1. 請根據自己的實際情況，填寫或選出適合的答案（在答案上畫“√”），注意每個問題都需要作答，并且只能選一個答案；

2. 答案為A、B、C、D、E五個選項，每一個備選答案的含義如下：

A 非常符合：并不意味著這一陳述所描述的情況總是發生在你身上，而是指幾乎在所有情況下這一陳述對你來說是符合的

B 符合：指在一般情況下這一陳述對你來說是符合的

C 不確定：指半數情況下這一陳述對你來說是符合的

D 不符合：指在一般情況下這一陳述對你來說是不符合的

E 非常不符合：指幾乎在所有情況下這一陳述對你來說是不符合的

3. 以下各題答案無好壞對錯之分，回答結果只為科學研究所用，不作為其它依據；

4. 此次調查采取匿名做答，我們將對回答結果絕對保密，請務必認真、如實回答每一個問題，你的回答對我們的研究非常重要．

基本信息

學校：???班級：???性別：???年齡：

調查項目

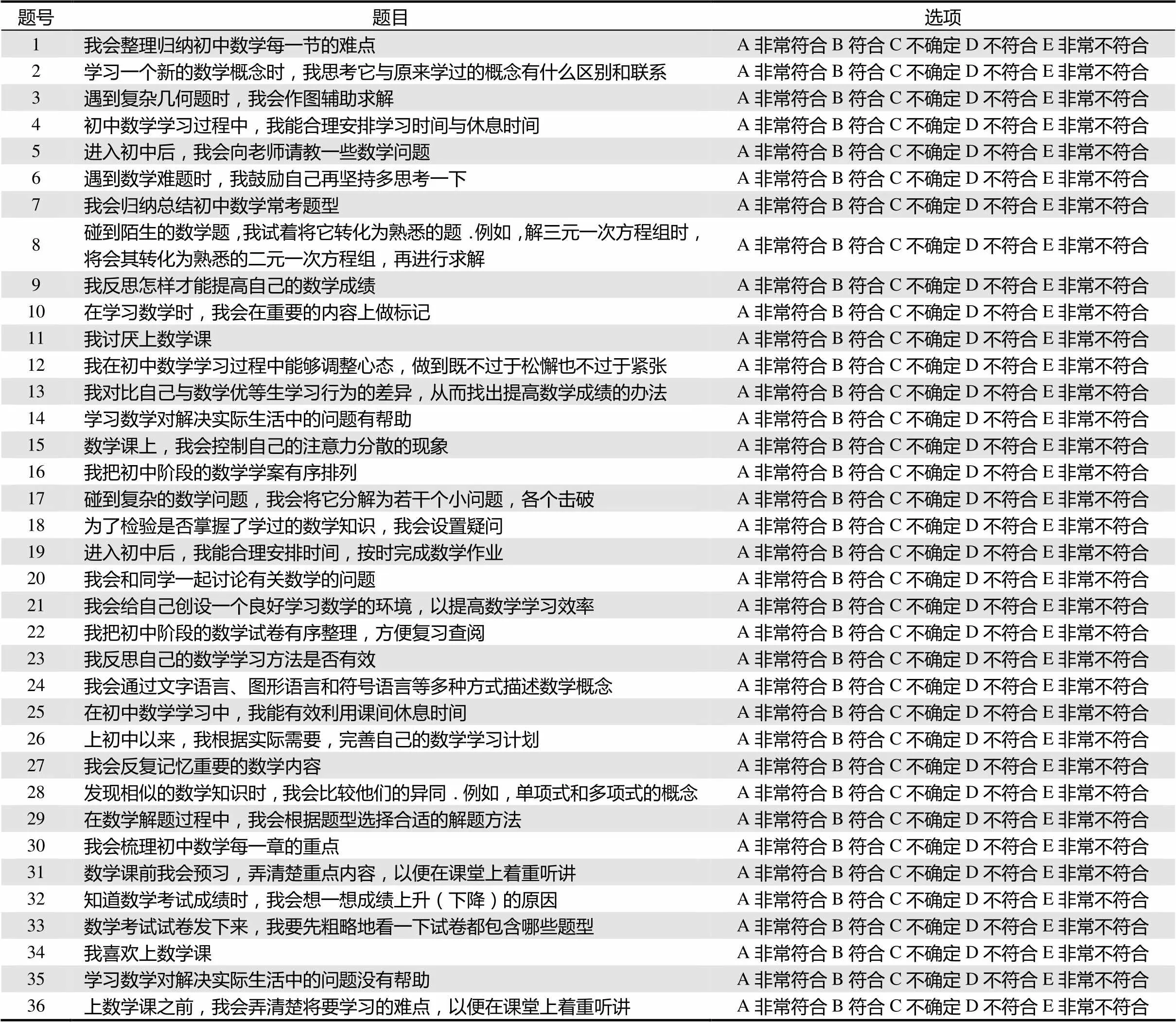
題號題目選項 1我會整理歸納初中數學每一節的難點A非常符合B符合C不確定D不符合E非常不符合 2學習一個新的數學概念時，我思考它與原來學過的概念有什么區別和聯系A非常符合B符合C不確定D不符合E非常不符合 3遇到復雜幾何題時，我會作圖輔助求解A非常符合B符合C不確定D不符合E非常不符合 4初中數學學習過程中，我能合理安排學習時間與休息時間A非常符合B符合C不確定D不符合E非常不符合 5進入初中后，我會向老師請教一些數學問題A非常符合B符合C不確定D不符合E非常不符合 6遇到數學難題時，我鼓勵自己再堅持多思考一下A非常符合B符合C不確定D不符合E非常不符合 7我會歸納總結初中數學常考題型A非常符合B符合C不確定D不符合E非常不符合 8碰到陌生的數學題，我試著將它轉化為熟悉的題．例如，解三元一次方程組時，將會其轉化為熟悉的二元一次方程組，再進行求解A非常符合B符合C不確定D不符合E非常不符合 9我反思怎樣才能提高自己的數學成績A非常符合B符合C不確定D不符合E非常不符合 10在學習數學時，我會在重要的內容上做標記A非常符合B符合C不確定D不符合E非常不符合 11我討厭上數學課A非常符合B符合C不確定D不符合E非常不符合 12我在初中數學學習過程中能夠調整心態，做到既不過于松懈也不過于緊張A非常符合B符合C不確定D不符合E非常不符合 13我對比自己與數學優等生學習行為的差異，從而找出提高數學成績的辦法A非常符合B符合C不確定D不符合E非常不符合 14學習數學對解決實際生活中的問題有幫助A非常符合B符合C不確定D不符合E非常不符合 15數學課上，我會控制自己的注意力分散的現象A非常符合B符合C不確定D不符合E非常不符合 16我把初中階段的數學學案有序排列A非常符合B符合C不確定D不符合E非常不符合 17碰到復雜的數學問題，我會將它分解為若干個小問題，各個擊破A非常符合B符合C不確定D不符合E非常不符合 18為了檢驗是否掌握了學過的數學知識，我會設置疑問A非常符合B符合C不確定D不符合E非常不符合 19進入初中后，我能合理安排時間，按時完成數學作業A非常符合B符合C不確定D不符合E非常不符合 20我會和同學一起討論有關數學的問題A非常符合B符合C不確定D不符合E非常不符合 21我會給自己創設一個良好學習數學的環境，以提高數學學習效率A非常符合B符合C不確定D不符合E非常不符合 22我把初中階段的數學試卷有序整理，方便復習查閱A非常符合B符合C不確定D不符合E非常不符合 23我反思自己的數學學習方法是否有效A非常符合B符合C不確定D不符合E非常不符合 24我會通過文字語言、圖形語言和符號語言等多種方式描述數學概念A非常符合B符合C不確定D不符合E非常不符合 25在初中數學學習中，我能有效利用課間休息時間A非常符合B符合C不確定D不符合E非常不符合 26上初中以來，我根據實際需要，完善自己的數學學習計劃A非常符合B符合C不確定D不符合E非常不符合 27我會反復記憶重要的數學內容A非常符合B符合C不確定D不符合E非常不符合 28發現相似的數學知識時，我會比較他們的異同．例如，單項式和多項式的概念A非常符合B符合C不確定D不符合E非常不符合 29在數學解題過程中，我會根據題型選擇合適的解題方法A非常符合B符合C不確定D不符合E非常不符合 30我會梳理初中數學每一章的重點A非常符合B符合C不確定D不符合E非常不符合 31數學課前我會預習，弄清楚重點內容，以便在課堂上著重聽講A非常符合B符合C不確定D不符合E非常不符合 32知道數學考試成績時，我會想一想成績上升（下降）的原因A非常符合B符合C不確定D不符合E非常不符合 33數學考試試卷發下來，我要先粗略地看一下試卷都包含哪些題型A非常符合B符合C不確定D不符合E非常不符合 34我喜歡上數學課A非常符合B符合C不確定D不符合E非常不符合 35學習數學對解決實際生活中的問題沒有幫助A非常符合B符合C不確定D不符合E非常不符合 36上數學課之前，我會弄清楚將要學習的難點，以便在課堂上著重聽講A非常符合B符合C不確定D不符合E非常不符合

[責任編校：周學智]

Design of Mathematics Learning Strategies Questionnaire for Junior High School Students

WANG Guang-ming, LIU Dan

(Teacher Education College, Tianjin Normal University, Tianjin 300387, China)

Through the literature review, the existing questionnaires or scales, and the opinions of well-known experts, Junior High School Students’ Mathematics Learning Strategy was divided into three dimensions: cognitive strategies, meta-cognitive strategies and resource management strategy, and we establish an operational definition of 10 sub-dimensions. We form the original questionnaire by the operational definition and the existing questionnaires or scales. Through data collection four times, project analysis, confirmatory factor analysis, exploratory factor analysis, and modify the questions in the questionnaire, eventually forming the. The questionnaire had good reliability and validity index, which could be used as an effective tool to measure the level of mathematics learning strategies for junior high school students.

junior high school; mathematics learning strategies; the design of questionnaires; scale

G449

A

1004–9894（2017）03–0019–06

2017–05–11

天津市2016年度哲學社會科學規劃重點課題——立德樹人背景下中學生學科核心素養測評——以語數外為例（TJJX16-007）

王光明（1969—），男，天津人，教授，博士生導師，主要從事數學課程與教學論研究．