基于關聯變量時滯分析卷積神經網絡的生產過程時間序列預測方法

張浩，劉振娟，李宏光，楊博，路潔

?

基于關聯變量時滯分析卷積神經網絡的生產過程時間序列預測方法

張浩1，劉振娟1，李宏光1，楊博1，路潔2

（1北京化工大學信息科學與技術學院，北京 100029；2中國自動化控制系統總公司，北京 100026）

生產過程通常具有大時滯、非線性、多變量耦合等特點，往往難以建立準確的時間序列預測模型。基于生產過程歷史數據，提出了一種采用關聯變量時滯分析卷積神經網絡（CNN）的生產過程時間序列預測方法，首先選取合適的關聯變量并對關聯變量與輸出進行時滯分析，然后利用時滯分析結果確定關聯變量時間窗的大小，最后建立合適的CNN模型對時間序列進行預測。某反應精餾過程實驗表明，此方法對于大時滯系統的長步長時間序列預測具有較好的準確性。

神經網絡；預測；關聯變量；時滯系統；反應精餾

引 言

生產過程時間序列的準確預測對于提高過程控制與優化品質具有重要的作用[1]，然而復雜的生產過程存在大量非線性單元，各個單元間互相關聯耦合，以及由于傳輸管道和積分作用造成較大的時滯，使得很難建立精準的機理模型[2]。為此，利用DCS記錄的歷史數據建立生產過程的時間序列預測模型成為研究的熱點方法。

傳統的數據驅動時間序列預測方法多是針對輸出序列自身的短時間預測，如自回歸積分滑動平均模型（ARIMA）、向量自回歸（VAR）、支持向量機（SVM）、三次指數平滑法（Holt-Winters）[3-8]。另外，基于神經網絡的時間序列預測方法也引起了研究者的重視，如Liu等[9]提出了基于BP神經網絡的動態時間序列預測模型，利用兩個相同結構的BP網絡分別進行在線預測和訓練，實現對NPP操作參數的時間序列的單步預測；Li等[10]提出了結合貝葉斯適應的神經網絡模型預測短時間風速。然而，這些算法并不適用于多步或大步長預測。

多步長時間預測存在較大的不確定性，針對多步時間序列預測，常見的方法有兩類[11-12]。

（1）迭代法：利用單步時間序列的預測方法預測出下一時刻的值，并將其不斷迭代到下步計算，實現多步預測，迭代法會隨著算法迭代次數的增加不斷增加不確定性，造成誤差累加。

（2）直接法：直接利用輸入預測多步的時間序列值，直接法對算法的準確性要求較高。

針對多步預測，Xiao等[13]提出了一種動態貝葉斯網絡的方法，而算法準確性有待提高；Bontempi[14]提出了一種多輸入多輸出（MIMO）預測模型；Sorjamaa等[15]提出了DirRec策略；以上方法在輸入維度提升時，算法復雜度過高。

生產過程中存在著許多相關變量，如果不進行處理會對時間序列預測造成干擾并增加運算量。常見的關聯分析方法包括基于過程機理的分析和基于過程數據的分析。另外，生產過程一般具有大時滯，直接利用關聯變量預測，會出現數據錯位、遺漏數據信息等問題。此時需要進行時滯分析，根據時滯分析結果，選取合適的時間窗進行預測。互相關分析（cross-correlation analysis，CCA）以滑動時間窗的方式計算不同時間差下相關性，取得最大相關性對應的時間差作為滯后時間，是一種常見的時滯分析方法[16]。Yan等[17]提出了一種基于互相關分析與小波變換的時滯分析方法；Person等[18]進行了基于互相關分析的肌肉電活動分析。

近年來，深度學習[19]得到了迅速發展，常見的深度學習方法有卷積神經網絡（convolutional neural network，CNN）、循環神經網絡（recurrent neural network，RNN）、RNN的改進算法LSTM（long short-term memory）、深度置信網絡（deep belief network，DBN），其中，CNN及LSTM/RNN算法在圖像識別、語音處理和自然語言處理等方面取得了顯著成就[20-25]。近年來，研究者也開始關注深度學習算法在控制領域中的應用[26-31]。

針對生產過程，提出了一種采用關聯變量時滯分析的CNN時間序列預測方法，對于多維輸入非平穩多步長預測時有著較好的準確性和實時性。首先，對生產過程中關聯變量進行時滯分析，利用滯后時間選擇關聯變量時間窗，提高了預測的精度；其次，選擇合適的卷積核大小對輸入數據進行卷積計算，以反映生產過程各變量之間的相互耦合；最后，選擇合適的激活函數，以處理生產過程的非線性特性。

1 生產過程關聯變量的時滯分析

1.1 時間序列預測方法

傳統的時間序列預測方法，如ARMA（自回歸移動平均）、VAR(向量自回歸)、Holt-Winters（三次指數平滑法）等，多是針對輸出序列自身的預測，如

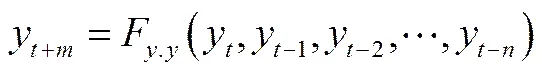
式中，y代表當前時刻的值；是預測步長；是時間窗的大小。此時間序列預測稱為-方法。

式(1)中，時間窗大小的值是時間序列預測中十分重要的參數。在LSTM神經網絡中，能自動選取合適的變步長進行計算。但對于大部分算法如CNN和BP等則需要首先設定好步長。目前常見的方法是利用試錯法（trial-and-error）不斷進行試驗調整，以選取合適的值[32-33]。

方法適合應用于平穩短期預測，具有算法復雜度低的優點。但是生產過程中普遍存在著多變量耦合的特征，時間序列往往并非僅僅與自身序列相關，因此需要考慮利用關聯變量協助預測、提高算法的準確性。

結合關聯變量的預測針對不同的輸入情況，可建立3種不同的方法。

第1種方法是僅僅利用關聯變量直接對待預測時間變量進行多步預測，其表達式可概括如下

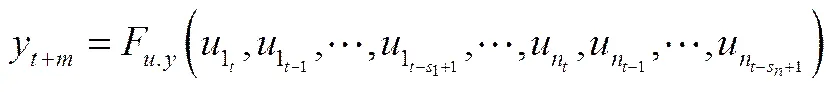
這稱為方法。研究表明，方法能預測的變化趨勢，但在對積分作用明顯時，預測曲線與實際曲線往往會出現上下的錯位。

第2種方法是為了提高在積分作用較大的情況下方法的準確性，基于差分思想通過輸入序列來預測輸出序列，即-方法，其表達式可概括如下

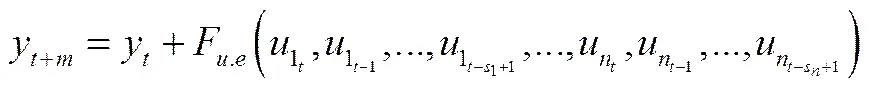
在預測步長較短時，-方法的準確度得到了提高，但在預測步長較大時，準確度并不高。

第3種方法是利用、一起作為輸入，預測時刻后的值，稱為方法，其表達式可概括如下

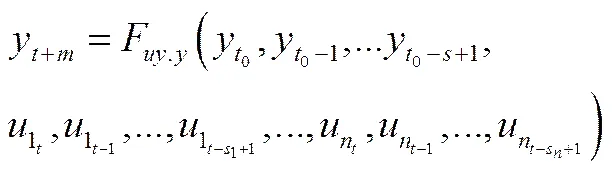
由于利用了最多的信息，相比其他方案具有更好的效果，特別是對于較大的預測步長，能更好地提升預測結果。

1.2 關聯變量的時滯分析

實際的生產過程含有大量的相關變量，互相關分析（CCA）是進行變量相關分析的一種有效方法，與此同時，CCA還可以提取關聯變量的時滯信息。

互相關函數（cross-correlation function，CCF）如下

式中，和分別是備選關聯變量和輸出；是序列長度；μ、μ是均值；σ、σ是方差。

樣本的CCF期望可由下式估計

其中，s、s分別是、的標準差。

時間滯后是選取時間序列時間區間的重要參考量。在生產過程中，往往需要同時考慮純滯后與容量滯后的影響。純滯后是由于調節機構的位置距被調參數所在的容積有一段距離，能量的傳輸需要一定的時間而產生的。被調參數開始變化的時刻落后于擾動出現的時刻，這個滯后的時間稱為純滯后。容量滯后一段是由于物料或能量的傳遞需要通過一定阻力而引起的，即對象受到一定的作用后，能量從不穩定到再次穩定的過程。如圖1所示，其中1為純滯后，2為容量滯后，為總滯后，等于純滯后與容量滯后之和。

合適的時間窗大小應當選取等于實際總滯后。但是目前沒有合適的算法分別準確計算。在存在容量滯后的情況下，直接利用CCA算法所得的延時接近但并不等于實際總滯后，如果選擇當作相關變量的時間窗，在實際時間滯后大于CCA算法計算的的情況下，可能會遺漏關聯信息。因此應選取大于的值作為的時間窗大小，可以考慮將乘以一個大于1的修正系數作為的值，即=×(>1)。

2 CNN時間序列預測方法

2.1 CNN結構與算法

卷積神經網絡（CNN）由多個卷積層、pooling層和全連接層級聯而成，卷積層可以提取輸入特征，利用多個卷積核對輸入進行卷積運算，輸出同等數量的特征圖，卷積層具有權值共享和局部感知的特點。Pooling層是一個下采樣層，常見的pooling方式有max-pooling、mean-pooling和stochastic- pooling。在經過多次卷積與pooling后，經全連接層運算得到網絡輸出。與其他神經網絡相似，在全連接層與Pooling層后添加合適的激活函數能提高網絡的非線性擬合能力。同時CNN的訓練依然是采用BP算法，調整各層權值與偏置。

CNN方法在處理多維度數據如圖像處理方面具有優勢，圖2是Geoffrey提出的AlexNet模型[20]，它是一個經典CNN網絡結構。

在處理多維時間序列時，CNN局部感知、權值共享以及下采樣的特點能減少大量參數個數，大幅提高運算效率。參考AlexNet模型，本文將在每個Pooling層及全鏈接層后加入Relu激活函數，并加入Dropout層減弱過擬合。

在訓練CNN時，這里選取Euclidean Loss作為BP的損失函數，即

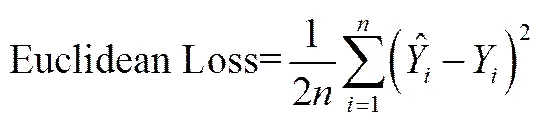
同時選擇Relu為激活函數，在BP算法中使用Sigmoid激活函數很容易造成梯度消失或者梯度爆炸的情況，Relu憑借其稀疏性改善了這個問題，即

(8)

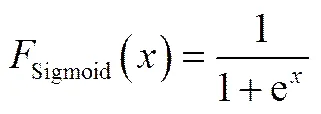
2.2 基于的時間序列預測方法

CNN算法在時間序列預測中有以下優勢：首先，CNN中卷積層的存在能夠處理多維輸入之間的相互耦合關系，進而增加算法的準確性；其次，CNN中的激活函數使得其能有效擬合非線性函數，而全連接層的加入進一步提升了網絡的擬合能力；最后，相比傳統全連接神經網絡，CNN卷積層權值共享、局部感知的特點以及pooling層下采樣的特點，使得CNN算法的復雜度遠低于全連接神經網絡。因此在根據時滯分析選取合適的輸入時間窗后，利用CNN進行時間序列預測是一種可行的有效方案。

在利用CNN進行生產過程時間序列預測時，首先需要確定網絡的輸入。對于模型，一般使用trial-and-error的方式選取時間窗，確定網絡的輸入；對于模型，首先利用CCA算法，選取與待預測時間序列（輸出）互相關系數大于閾值的變量作為相關變量，然后利用CCA算法求得的時滯信息，確定時間窗；同理，可確定-模型與模型的輸入。

對于模型的CNN預測模型網絡結構，考慮到輸入維度的特點，不同于傳統圖像處理方法中使用方形（×）的卷積核尺寸，可以選取長條形卷積核和pooling窗尺寸，具體步驟如下：

（1）分析數據，利用trial-and-error方式選取合適的時間窗。

（2）利用幾個具有長條形尺寸卷積核和pooling窗的卷積層和pooling層，將輸入寬度降到較小的值。

（3）添加全連接層得到網絡輸出。

（4）訓練模型，根據效果調整網絡結構。

圖3是一個時間窗為的模型CNN模型結構，其中Conv是卷積層的簡寫，p是對應的第個卷積核的長度，MP是max-pooling層的簡寫，q分別是對應的第個Pooling窗口長度，C是第個卷積層中特征圖的個數。F是全鏈接層輸出個數。

對于和模型，CNN結構設計方法相同。在只有一個關聯變量時，網絡的設計與Y-Y型類似，只是在確定時間窗的時候選取CCA算法。

考慮多個關聯變量的情況，首先利用CCA算法選取互相關系數大于閾值的變量作為相關變量，然后選取這些關聯變量最大的時滯，乘以修正系數作為時間窗長度的值。對于網絡結構，本文提出在第1個卷積層選擇寬度等于輸入維度的矩形卷積核，將輸入寬度變為1。對于個相關變量，時間窗長度為的情況，首先利用×的卷積核尺寸，將輸入寬度變為1，然后利用模型的CNN設計步驟進行設計。為此，設計和型網絡結構的步驟如下：

（1）分析數據，利用CCA算法，選取這些關聯變量最大的時滯，乘以修正系數作為時間窗長度的值。

（2）在第1個卷積層利用×大小的卷積核將輸入寬度變為1。

（3）利用模型的CNN設計步驟進行后續的網絡結構設計。

如圖4所示。

對于模型，可行的思路是將與平等的作為輸入，采用/的網絡結構設計。

2.3 基于CNN的時間序列預測實現

CNN離線訓練的步驟是，首先從生產過程中取得歷史數據，對數據進行分析和預處理。預處理包括異常值剔除、數據歸一化以及利用CCA得到關聯變量和時滯變量。然后根據數據的特點設計CNN網絡結構，將處理好的數據送入網絡進行訓練。達到訓練迭代次數后檢驗結果是否符合要求。如果不符合，則調整網絡結構重新訓練，直到達到滿意效果。離線訓練過程如圖5所示。

在線進行時間預測是CNN前傳的過程。首先從生產過程中的DCS中獲取實時數據，并將數據按照訓練預處理時的方式進行歸一化處理，然后將歸一化后的數據送入卷積神經網絡進行預測得到輸出，再將輸出結果反歸一化，循環等待下一時刻數據的傳入。在線預測過程如圖6所示。

3 實例研究

考慮如圖7所示的某反應+精餾過程模型，0和1是兩個進料量，經過反應器X后生成物由管道a傳輸至精餾塔A，塔釜餾出液經管道b傳輸至存儲罐A，再經管道c輸送至精餾塔B，其塔釜液送至儲罐B。由于測量及工藝限制，部分變量如精餾塔A側線出料流量2和塔A液位0等不能直接測量。采樣周期為5 s，獲取了60000組數據，隨機選取50000組用于訓練，其余10000組用于測試。

為了預測精餾塔A的液位1的時間序列，首先利用CCA算法，從多個可測變量中篩選出關聯變量。這里，經CCA算法從7個可測變量中選取了2個關聯變量，同時利用CCA算法得出它們的最大時滯，見表1。

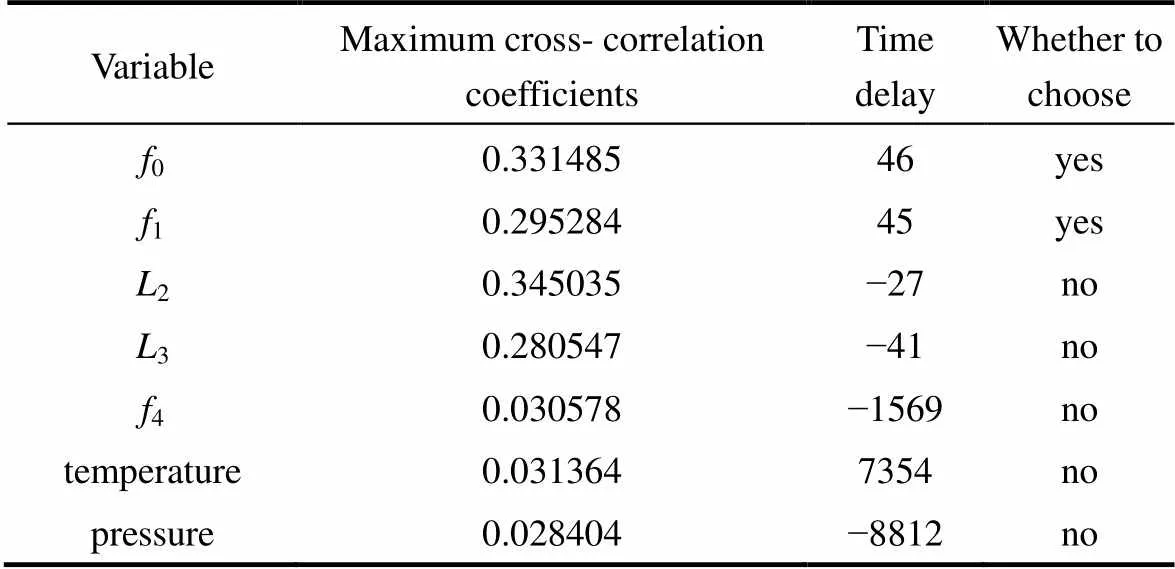
表1 關聯變量選取及時滯分析

其中，將最大關聯系數大于閾值0.2，且時滯大于0的變量選為關聯變量即0和1。對于///模型，選擇修正系數=1.1，則輸入時間窗大小=×=16×1.1≈50。而對于模型利用試錯法選取時間窗大小。

3.1模型

利用試錯法，選取=26，設計網絡結構如圖8所示。

分別利用模型做了單步預測、短步長預測（預測時間為5）、長步長預測（預測時間為20）。輸出的預測結果曲線和平方誤差曲線分別如圖9～圖11所示。

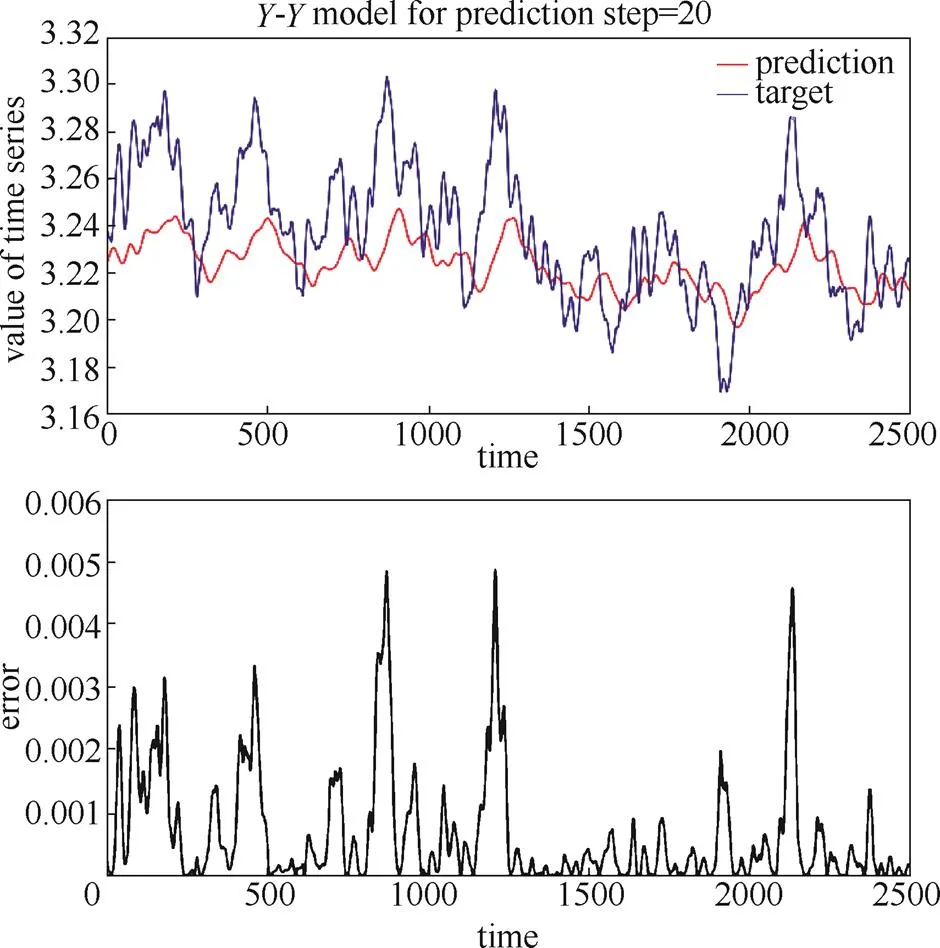
圖11 長步長Y-Y預測

實驗結果顯示，隨著預測步長的增加，誤差逐漸增大。可見，模型預測難以有效地預測變量的變化趨勢。

3.2模型

利用CCA算法算得的時間窗大小=50，設計網絡結構如圖12所示。

分別利用模型做了短步長預測（預測時間為5）、長步長預測（預測時間為20）。輸出的預測結果曲線和平方誤差曲線分別如圖13、圖14所示。

實驗結果顯示，能預測變化趨勢，但由于積分作用的存在容易出現上下偏差。

3.3模型

利用CCA算法算得的時間窗大小=50。模型結構與模型一致。分別利用模型做了短步長預測（預測時間為5）、長步長預測（預測時間為20）。輸出的預測結果曲線和平方誤差曲線分別如圖15、圖16所示。

Fig .15 Short-time predictions ofmodels

實驗結果顯示，在短步長情況下，能提高預測效果，但在長步長預測時偏差較大。

3.4模型

利用CCA算法算得的時間窗大小=50，模型結構如圖17所示。

分別利用-模型做了短步長預測（預測時間為5）、長步長預測（預測時間為20）。輸出的預測結果曲線和平方誤差曲線分別如圖18、圖19所示。

實驗結果顯示，模型在短步長與長步長情況下都有著較好的結果。

表2給出了各種模型的結果對比。

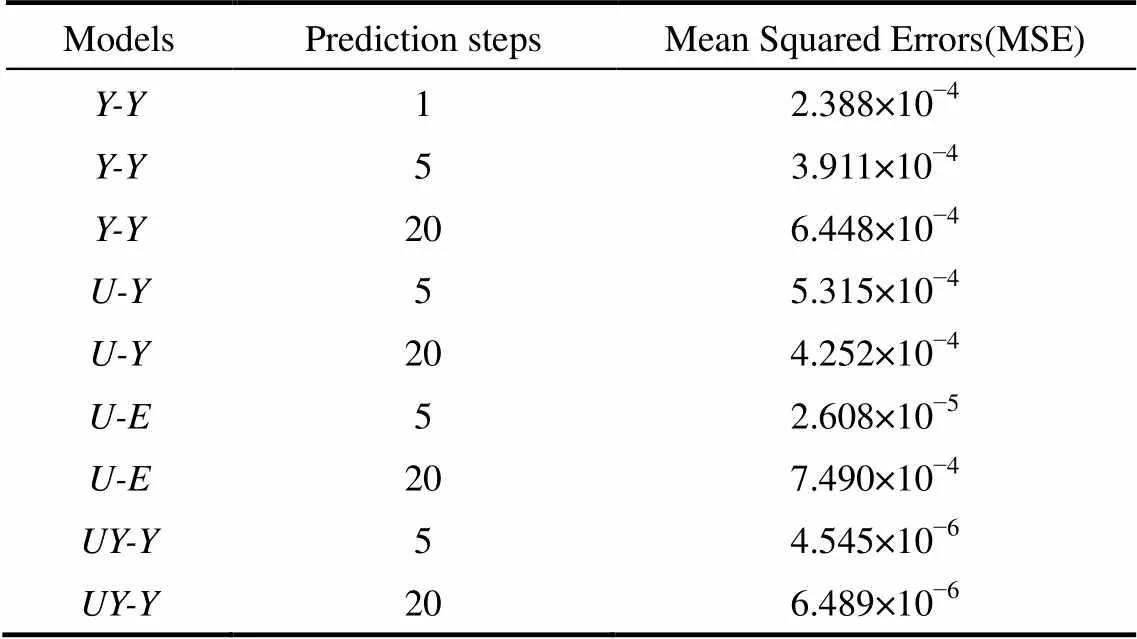
表2 不同算法誤差分析

3.5 對比實驗

此節利用ARMA、BP神經網絡（3個隱含層）與本文所提的CNN算法進行預測對比實驗。同樣針對反應+精餾過程，進行20步預測，選取10000組數據進行測試。其中100組連續數據的預測結果曲線如圖20所示。

CNN、BP、ARMA預測的平方誤差分別為：6.489×10?6、7.546×10?6、7.167×10?4（10000組數據的平均平方誤差）。同時在i5-6300hq的CPU上測得（不使用GPU加速）CNN、BP、ARMA平均單次預測耗時分別為1.969、3.722、0.0206 ms。

實驗結果顯示，在長步長（20）預測時，BP神經網絡與CNN均能較好地進行預測。相比神經網絡算法，雖然ARMA算法有著較高的時效性，卻不能達到良好的預測效果。由于CNN中卷積層權值共享、局部感知的特點以及pooling層下采樣的特點，使得在輸入維度升高時，CNN算法的預測耗時低于BP算法。

4 結 論

針對長步長時間序列預測的問題，提出了一種基于CNN的協關聯變量的時間序列預測方法。對于大時滯生產過程，解決了傳統算法在長步長時間序列預測時準確性差的問題，以及當輸入維度升高時，算法復雜度過高的問題。基于關聯變量時滯分析的CNN預測方法能夠有效地利用得到的信息，提高時間序列預測的準確性，這也通過實驗過程測試得到了有效的驗證。

References

[1] 李宏光, 臧灝. 管式加熱爐多模型神經網絡預測控制[J]. 控制工程, 2012, 19(4): 650-653. LI H G, ZANG H. Multi-model adaptive neural network based predictive control of furnace[J]. Control Engineering of China, 2012, 19(4): 650-653.

[2] ZHANG X X, XU J, ZHANG S,. Experiment on parameter identification of a time delay coupled nonlinear system[J]. IFAC Papersonline, 2015, 48(11): 694-699.

[3] SZMIT M, SZMIT A. Use of holt-winters method in the analysis of network traffic case study[J]. Communications in Computer & Information Science, 2011, 160: 224-231.

[4] ROSSI M, BRUNELLI D. Forecasting data centers power consumption with the Holt-Winters method[C]// Process of IEEE Workshop on Environmental, Energy and Structural Monitoring Systems IEEE, 2015: 210-214.

[5] PRAVILOVIC S, APPICE A, MALERBA D. Integrating Cluster Analysis to the ARIMA Model for Forecasting Geosensor Data[M]. Foundations of Intelligent Systems, 2014: 234-243.

[6] 王鋒, 李宏光, 臧灝. 基于Logistic和ARMA模型的過程報警預測[J]. 化工學報, 2012, 63(9): 2941-2947. WANG F, LI H G, ZANG H. Process alarm prognosis based on Logistic and ARMA models[J]. CIESC Journal, 2012, 63(9): 2941-2947.

[7] LENG X Z, WANG J H, JI H B,. Prediction of size-fractionated airborne particle-bound metals using MLR, BP-ANN and SVM analyses[J]. Chemosphere, 2017, 180: 513.

[8] WANG L, TING M F, CHAPMAN D,. Prediction of northern summer low-frequency circulation using a high-order vector auto-regressive model[J]. Climate Dynamics, 2015, 46: 1-17.

[9] LIU Y K, XIE F, XIE C L,. Prediction of time series of NPP operating parameters using dynamic model based on BP neural network[J]. Annals of Nuclear Energy, 2015, 85: 566-575.

[10] LI G, SHI J, ZHOU J Y. Bayesian adaptive combination of short-term wind speed forecasts from neural network models[J]. Renewable Energy, 2011, 36(1): 352-359.

[11] ATIYA A F, EL-SHOURA S M, SHAHEEN S I,. A comparison between neural-network forecasting techniques-case study: river flow forecasting[J]. IEEE Transactions on Neural Networks, 1999, 10(2): 402-409.

[12] CHEVILLON G. Direct multi-step estimation and forecasting[J]. Journal of Economic Surveys, 2007, 21(4): 746-785.

[13] XIAO Q K, XING L, SONG G. Time series prediction using optimal theorem and dynamic Bayesian network[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(23): 11063-11069.

[14] BONTEMPI G. Long term time series prediction with multi-input multi-output local learning[J]. Proceedings of European Symposium on Time, 2008: 145-154.

[15] SORJAMAA A, LENDASSE A. Time series prediction using dirrec strategy[C]// Esann 2006, European Symposium on Artificial Neural Networks, Bruges, Belgium, Proceedings. DBLP, 2006: 143-148.

[16] YANG F, DUAN P, SHAH S L,. Capturing connectivity and causality in complex industrial processes[C]// Springer Publishing Company, Incorporated, 2014: 45-46.

[17] YAN H, ZHANG Y P, YANG Q. Time-delay estimation based on cross-correlation and wavelet denoising[C]// Chinese Intelligent Automation Conference, 2013: 841-848.

[18] PERSON R S, MISHIN L N. Auto- and cross- correlation analysis of the electrical activity of muscles[J]. Medical & Biological Engineering & Computing, 1964, 2(2): 155.

[19] SCHMIDHUBER J. Deep learning in neural networks: an overview[J]. Neural Networks, 2015, 61: 85-117.

[20] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]// International Conference on Neural Information Processing Systems, 2012: 1097-1105.

[21] SOUTNER D, MüLLER L. Application of LSTM Neural Networks in Language Modelling[M]. Text, Speech, and Dialogue. Springer Berlin Heidelberg, 2013: 105-112.

[22] MORTON J, WHEELER T A, KOCHENDERFER M J. Analysis of recurrent neural networks for probabilistic modeling of driver behavior[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 99: 1-10.

[23] LIU W, ANGUELOV D, ERHAN D,. SSD: Single shot multibox detector[C]// European Conference on Computer Vision. Springer International Publishing, 2016: 21-37.

[24] GIRSHICK R. Fast R-CNN[C]// IEEE International Conference on Computer Vision. IEEE Computer Society, 2015: 1440-1448.

[25] REN S Q, HE K M, GIRSHICK R,. Faster R-CNN: towards real-time object detection with region proposal networks[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2016, 39(6): 1137.

[26] 段艷杰, 呂宜生, 張杰, 等. 深度學習在控制領域的研究現狀與展望[J]. 自動化學報, 2016, 42(5): 643-654. DUAN Y J, Lü Y S, ZHANG J,. Deep learning for control: the state of the art and prospects[J]. Acta Automatica Sinica, 2016, 42(5): 643-654.

[27] 韓改堂, 喬俊飛, 韓紅桂. 基于遞歸模糊神經網絡的污水處理控制方法[J]. 化工學報, 2016, 67(3): 954-959. HAN G L, QIAO J W, HAN H G. Wastewater treatment control method based on recurrent fuzzy neural network[J]. CIESC Journal, 2016, 67(3): 954-959.

[28] ZHU Q X, JIA Y W, PENG D,. Study and application of fault prediction methods with improved reservoir neural networks[J]. Chinese Journal of Chemical Engineering, 2014, 22(7): 812-819.

[29] POUL A K, SOLEIMANI M, SALAHI S. Solubility prediction of disperse dyes in supercritical carbon dioxide and ethanol as co-solvent using neural network[J]. Chinese Journal of Chemical Engineering, 2016, 24(4): 491-498.

[30] HE Y L, XU Y, ZHAO Z Q,. Soft sensor of chemical processes with large numbers of input parameters using auto-associative hierarchical neural network[J]. Chinese Journal of Chemical Engineering, 2015, 23(1): 138-145.

[31] 安愛民, 劉云利, 張浩琛, 等. 微生物燃料電池的動態性能分析及其神經網絡預測控制[J]. 化工學報, 2017, 68(3): 1090-1098. AN A M, LIU Y L, ZHANG H T,. Dynamic performance analysis and neural network predictive control of microbial fuel cell[J]. CIESC Journal, 2017, 68(3): 1090-1098.

[32] SEDKI A, OUAZAR D, MAZOUDI E E. Evolving neural network using real coded genetic algorithm for daily rainfall-runoff forecasting[J]. Expert Systems with Applications, 2009, 36(3): 4523-4527.

[33] ZHANG G P. Time series forecasting using a hybrid ARIMA and neural network model[J]. Neurocomputing, 2003, 50: 159-175.

Process time series prediction based on application of correlated process variables to CNN time delayed analyses

ZHANG Hao1, LIU Zhenjuan1, LI Hongguang1, YANG Bo1, LU Jie2

(1College of Information Science & Technology, Beijing University of Chemical Technology, Beijing 100020, China;2China National Automation Control System Co., Beijing 100026, China)

It is often difficult to establish models for accurate time series prediction, as a result of time delay, nonlinearity, and multi-variable coupling characteristics in production processes. A time series prediction method was proposed by applying correlated process variables to time delayed analysis of convolutional neural network (CNN). First, appropriate correlated variables were selected and time series were analyzed between these variables and outputs. Then, results of time series analysis were employed to determine length of temporal time windows of associated variables. Finally, appropriate CNN models were established for time series prediction. Experimental results of a reaction distillation process showed good accuracy in time series prediction of long time frame and large time-delay processes.

neural networks; prediction; correlated variable; time-delay system; reactive distillation

10.11949/j.issn.0438-1157.20170197

TP 183

A

0438—1157（2017）09—3501—10

2017-02-28收到初稿，2017-06-01收到修改稿。

李宏光。

張浩（1992—），男，碩士研究生。

2017-02-28.

Prof. LI Hongguang, lihg@mail.buct.edu.cn