結合高光譜信息的土壤有機碳密度地統計模型

劉艷芳，宋玉玲，郭 龍，陳奕云，盧延年，劉 以

?

結合高光譜信息的土壤有機碳密度地統計模型

劉艷芳1,2,3，宋玉玲1,2,3，郭 龍4，陳奕云1,2,5,6※，盧延年1,2,3，劉 以1,2,3

（1. 武漢大學資源與環境科學學院，武漢 430079； 2. 武漢大學地理信息系統教育部重點實驗室，武漢 430079； 3. 數字制圖與國土信息應用工程國家測繪地理信息局重點實驗室，武漢 430079； 4. 華中農業大學資源與環境學院，武漢 430070； 5. 地球空間信息技術協同創新中心，武漢大學，武漢 430079； 6. 武漢大學蘇州研究院，蘇州 215123）

傳統線性回歸模型在借助光譜信息進行土壤屬性預測時，通常忽略了土壤自身所具有的空間異質性和依賴性，并且未考慮模型殘差的空間結構。針對以上不足，該文以江漢平原232個土壤樣本為研究對象，以土壤反射光譜為輔助變量，采用偏最小二乘回歸、普通克里格、協同克里格以及回歸克里格分別構建土壤有機碳密度預測模型，選取決定系數（2）、均方根誤差、標準差與預測均方根誤差比（ratio of performance to deviation，RPD）對模型預測精度進行對比評價。結果顯示，結合高光譜信息，且同時考慮殘差空間結構的回歸克里格模型表現優于其他模型，預測決定系數R為0.617，RPD為1.614。鑒于土壤光譜信息同時還具有測定簡單、省時、無損等優點，因此土壤光譜是土壤有機碳密度空間插值的理想輔助因子。

土壤；模型；光譜分析；土壤有機碳密度；偏最小二乘回歸；協同克里格；回歸克里格

0 引 言

土壤是地球陸地表層最為活躍的碳庫之一，是陸地生態系統的重要組成。農田土壤碳庫關系到國家糧食安全和生態農業可持續發展[1]，農田土壤碳儲量的變化及時空分異規律研究是當前地理信息科學、土地資源管理等學科的研究熱點。其中，土壤有機碳密度（soil organic carbon density，SOCD）是土壤碳儲量估算的重要參數，其時空信息的快速、高效獲取是未來地理國情監測和國土資源調查的重要發展方向。然而，土壤本身是一個開放的復雜系統，由于受復雜的成土過程、自然環境要素以及人類活動等因素的影響，在不同的地區SOCD存在各具特點的空間分異規律，環境要素與SOCD的關系表現出一定的空間異質性，因此，考慮模型殘差的空間結構特征對SOCD進行快速有效的預測具有積極的研究意義。

目前的研究主要采用野外采土樣結合實驗室化學分析的方法對SOCD進行測定，該方法操作耗時，步驟繁瑣，與現代農業精準監測、全面管理的需求不匹配。但可見—近紅外光譜測定分析能夠達到便捷準確、節約成本、精確度高的要求，逐漸成為土壤組分估算預測的新方法[2]。土壤有機質中包含大量的氫基團，而近紅外光譜可以很好地捕捉到有機質中含氫基團的變化，并根據光譜反射率的不同反推出含氫基團的數量特征，從而得到土壤有機質含量，最后將有機質含量和Bemmelen換算系數相乘[3]，得到土壤有機碳含量值，因此近紅外光譜在技術上為快速測定SOCD提供了可行性[4]。近年來基于光譜信息的土壤屬性的預測模型引起土壤和生態學者的關注[5]，由于其迅速、精確、無污染、不破壞樣本等諸多的優點在土壤領域得到迅速的發展。然而現有研究通常視土壤樣本為化學樣本，進而采用傳統線性回歸模型，如偏最小二乘回歸（partial least squares regression，PLSR）結合光譜信息進行土壤屬性的擬合和預測。例如，李耀翔等采用近紅外光譜技術對森林土壤有機碳含量進行研究[6-7]，表明結合光譜反射率能夠對土壤有機碳含量進行有效測算，但是僅采用PLSR模型進行估算，忽略了土壤屬性本身所具有的空間異質性。實際上土壤屬性的空間特征在進行土壤屬性預測及制圖中起到至關重要的作用。

當前進行土壤屬性預測制圖的方法主要有3種：1）以土壤發生學為理論基礎，以外部環境要素與土壤內在屬性協同變化關系為核心的土壤-環境模型[8-10]；2）基于空間信息的土壤屬性空間插值預測模型，例如普通克里格插值模型（ordinary kriging，OK）[11-15]；3）綜合模型，結合外部環境要素與土壤內在屬性及空間信息進行建模，例如協同克里格插值模型（co-kriging，COK）。土壤屬性的空間依賴性和異質性為構建土壤屬性預測模型提供了理論基礎和科學依據，同時也為克里格模型中的半變異函數提供選擇依據和準則，為此在構建土壤屬性模型的過程中充分考慮土壤屬性的空間信息有助于提高模型的精度和可行性。而土壤在形成、轉化和侵蝕的過程中受到多種自然環境和人為因素的影響，因此土壤-環境模型的發展也為預測土壤屬性的空間分布以及變化過程提供了一定的幫助[16-17]。但是由于克里格模型是借助于半變異函數的權重系數而建立的空間插值模型，因此在地形復雜或者屬性變化強烈的區域難以進行準確的建模和預測，并且克里格模型建模過程忽略了外界因素對土壤屬性的影響。土壤-環境模型在建模的過程中，由于不同的環境因素對土壤屬性的影響機理復雜，并且存在一定的時間滯后性，進而難以通過簡單、直接的線性關系對土壤屬性進行定量描述。因此，為了更好地揭示SOCD的空間分異規律，需要在建模過程中綜合考慮與SOCD相關的外在環境因子以及內在組分的外在反映（如土壤的反射光譜）。

在構建綜合模型進行土壤屬性預測時，有學者采用回歸克里格模型（regression kriging，RK），以光譜信息作為輔助變量，相對于環境變量而言可以更為直接地反映土壤屬性，并且模型同時考慮了殘差的空間依賴性，進而保證了基于最小二乘準則回歸模型的基本假定（殘差項相互獨立，互不相關）。Ge等[18]選取密西西比河奎特曼縣耕地類型的273個土壤樣本，探究近紅外光譜方法和地統計方法以及兩者結合對土壤屬性預測精度的影響，進行回歸克里格建模和主成分回歸建模，結果表明結合了光譜反射率和空間變異性的回歸克里格模型效果更好，決定系數2達到了0.65；對于傳統回歸模型無法準確預測的土壤屬性（如鉀、鈉、磷元素含量），回歸克里格模型也能得到較好的預測結果。Bilgili等[19]選取土耳其北部一個32 hm2的研究區域內的土壤樣本，進行PLSR、OK、COK、RK分別建模并進行對比分析，結果表明，光譜反射率結合地統計模型的預測效果更好，對土壤有機質的預測效果，COK、RK優于PLSR優于OK。然而，當前少有研究探究上述方法在SOCD預測制圖中的應用。

本文從SOCD具有空間依賴性和異質性這一土壤本質特征出發，選取采集自江漢平原的232個土壤樣本作為研究對象，嘗試以土壤屬性的光譜信息作為輔助變量，利用協同克里格模型和回歸克里格模型構建SOCD預測模型，同時與普通克里格模型和PLSR模型進行預測精度比較，探討土壤光譜信息和空間信息在SOCD建模中的作用，以期為SOCD的預測提供有效的參考信息和理論基礎。

1 材料與方法

1.1 研究區域概況

汊河鎮位于江漢平原中心，地理坐標位于29°55′～30°04′N，113°23′～113°33′E[20]，被選為研究區域。汊河鎮的地理面積約為153 km2，海拔范圍為2～35 m，屬亞熱帶季風氣候，也具有明顯的大陸性氣候特點，冬夏長，春秋短，四季分明，光照充足，雨量充沛，溫和濕潤，年均氣溫為16.6 ℃，年均降雨量達1 154 mm。江漢平原是典型的沖積平原，研究區域適合多種作物生長，是中國的一個重要農業地區。研究區的土壤母質層主要來源是河流沖積和湖泊沉積，土壤類型主要為水稻土和潮土，研究區區位及土壤樣本點的空間分布如圖1所示。

圖1 研究區區位及樣本點空間分布圖

Fig.1 Location of study area and spatial distribution of sample points

1.2 樣本制備與光譜測定

土壤樣本的采集工作于2013年7月完成，采集時使用隨機布點法布設232個樣點，每個樣點處在1 m2的方形范圍內的4個角及中心處使用木鏟采集5份表層土壤樣本（0～30 cm），混合均勻后取500 g作為該樣點土壤樣本，裝入自封袋中。此外，取部分土樣裝入鋁盒中，用于實驗室土壤含水量的測定。同時使用環刀采集環刀土一份裝入自封袋，用于土壤容重分析[20]，樣本采集點之間的最小間隔為100 m，其中耕地樣本130個、林地29個、園地28個、建設用地39個、荒地6個。

土壤樣本在實驗室內經過一系列預處理，包括風干、研磨和過0.15 mm篩等，之后分別進行光譜測定和化學方法分析。其中，土壤有機碳含量分析采用的化學方法是重鉻酸鉀氧化-分光光度法[21]。土壤有機碳密度的計算公式為

式中為土壤發生層數（文中取=1）；θ為第層土壤大于2 mm礫石的體積百分含量，%；p為第層土壤容重，g/cm3；C為第層土壤有機碳含量，g/kg；為第層土壤厚度，cm[20]。

土壤樣本在可見光—近紅外光譜（350～2 500 nm）區間內的光譜反射率由ASD FieldSpec3地物光譜儀獲得，光譜反射率的具體測量步驟與盧延年、陳奕云等的研究類似[2,22]。

1.3 光譜數據預處理

由于受到光譜儀自身誤差和測量環境噪聲的影響，光譜反射率不可避免地受到隨機噪聲、基線漂移以及多次散射效應等因素影響，這些因素可能影響最終建立模型的可靠性[4]。因此，光譜預處理是建模前的一個重要步驟。

本研究選取了5種光譜預處理方法，包括Savitzky-Golay平滑方法（S-G）、一階導數法（1st）和二階導數法（2nd）、標準正態變量變換處理方法（standard normal variate，SNV）和多元散射校正處理方法（multiplicative seater correction，MSC）[23-26]，以及它們的組合，比較了它們在SOCD的PLSR模型中對預測精度的影響，分別是S-G、S-G+MSC、S-G+SNV、S-G+1st、S-G+2nd、S-G+1st+MSC、S-G+2nd+MSC、S-G+1st+SNV、S-G+2nd+SNV。

1.4 建模方法

1.4.1 偏最小二乘回歸

由于光譜波段變量間往往存在多重共線性，直接使用最小二乘法擬合得到的回歸方程會產生嚴重失真。偏最小二乘回歸是一種多變量統計數據分析方法，它開辟了一種有效的途徑，在處理樣本容量小、解釋變量多、變量間存在多重共線性問題方法有獨特的優勢，已成為土壤有機碳等組分估算的常用方法[21,27]。

1.4.2 普通克里格模型

普通克里格法，是一種建立在區域化變量理論上的空間局部插值法，待估計點的值可以根據周圍一定范圍內觀測點的值加權得到。它的權重值是結合觀測值的變異函數，在無偏最優估計的思想和拉格朗日極小化原理指導下得到，且往往假設空間為各向同性。具體公式如下

權重取決于領域內樣點和目標點的相對位置，半變異函數可以描述數據點各變量的空間相關性和協方差結構，對未知樣點進行無偏、最優估計，無偏是指偏差的數學期望為0，最優是指估計值與實際值之差的平方和最小，公式如下

1.4.3 協同克里格模型

協同克里格對普通克里格進行了擴展，主要區別是添加了一個或多個與主變量（1）存在空間相關性的輔助變量（2），具體公式如下

本文的主變量是土壤有機碳密度，輔助變量是土壤可見—近紅外光譜反射率。

1.4.4 回歸克里格模型

回歸克里格法將觀測值看作代表確定性部分的趨勢項和代表隨機性部分的殘差項的加和，其中趨勢項由外界因素干擾產生，依據最小二乘法（ordinary least square，OLS）原理擬合目標變量和輔助變量的回歸方程，并得到各輔助變量參數；殘差項代表土壤屬性固有的隨機性，理論上呈正態分布，可以通過克里格插值得到任意一點的殘差。則預測點屬性值可由輔助變量加權值與該點殘差加和得到[19]。其過程可表示為

1.5 模型評價

為了最大限度的檢驗模型對未知樣點的估測能力，文章選擇1∶1的比例來構建建模樣本集與驗證樣本集，即根據Kennard-Stone算法將232個總體樣本劃分為建模樣本集（119個樣本）和驗證樣本集（113個樣本）[28-29]。

模型的精度選取決定系數2、均方根誤差（root mean squares error，RMSE）、預測均方根誤差（root mean squares error of prediction，RMSEP）、標準差與預測均方根誤差比（ratio of performance to deviation，RPD）等參數來衡量。RPD是驗證樣本集SOCD的標準差與預測均方根誤差RMSEP的比值，一般認為，RPD小于1.4時，模型難以對樣本進行有效預測；RPD介于1.4～2之間，模型可以對樣本進行粗略地預測；RPD大于等于2時，模型預測效果極好[22,30-31]。計算公式如下

式中為驗證點個數，y為第個樣本的測量值，為第個樣本的預測值，為測量值的均值。

2 結果與分析

2.1 SOCD描述性統計

土壤總體樣本、建模樣本集和驗證樣本集的SOCD數據分布特征基本相近，保證了建模數據集的代表性。標準差和變異系數可以表示土壤樣本數據與平均值的離散度，3個數據集的標準差分別為1.37、1.30和1.40 kg/m2，變異系數分別為29.70%、29.83%和28.39%（表1），三者之間的標準差和變異系數差距很小，保證了數據之間離散程度的一致性。3個數據集的偏度系數分別為0.03、0.06和?0.08，峰度系數分別為?0.72、?0.52和?0.89（表1），均接近于0，這表明3個數據集中的土壤有機碳密度的分布特征符合正態分布特征，說明建模數據可以滿足克里格插值模型所要求的二階平穩性，保證了建模結果的準確可靠性。

表1 不同樣本集土壤有機碳密度的基本統計特征

2.2 PLSR建模中光譜數據預處理效果

不同光譜預處理條件下的模型評價結果如表2所示。對未經預處理的原始光譜（即反射率光譜）進行建模，可以得到建模集決定系數（2ofcalibration，2-Cal）為0.74，留一交叉驗證決定系數2-CV（2of leave-one-out cross validation）為0.603，驗證集決定系數（2ofprediction，2-Pred）為0.558。這說明光譜反射率對SOCD的變異具有較好的指示作用。由于原始光譜存在的噪聲、漂移因素對建模存在一定的干擾，因此對原始光譜進行合適的預處理可以進一步提高模型的預測精度。單純地采用Savitzky-Golay平滑方法，或者在對原始光譜進行Savitzky-Golay平滑的基礎上，結合標準正態變換（SNV）或多元散射校正（MSC），建立的模型精度未有明顯提高。而對光譜數據進行一階和二階微分預處理后再結合S-G、SNV、MSC等預處理方法進行建模，2-Cal可達0.909，建模精度有了明顯的提高，并且模型主成分數為4，與無預處理模型的8個主成分數相比也有了明顯的降低，這說明一階和二階微分方法對光譜數據的預處理起著至關重要的作用。預處理之后的土壤光譜與SOCD的皮爾遜相關系數（Pearson’s coefficient）絕對值的最大值有明顯提高，突出了光譜特征波段與SOCD之間的相關關系，進而可以使用較少的光譜主成分包含更多的SOCD變異信息（圖2）。綜合考慮建模和留一交叉驗證精度（所建模型需要對建模數據變異具有良好的解釋能力，即較高的2-Cal和2-CV）以及驗證樣本集檢驗精度（即模型需要具有良好的預測能力，如RPD>1.4）。因此，認為Savitzky-Golay平滑處理、一階微分和標準正態變換的組合是最佳預處理方法。

2.3 SOCD預測模型的建立

2.3.1 利用PLSR構建SOCD預測模型

利用S-G+1st+SNV預處理方法對土壤光譜反射率進行變換之后，采用PLSR方法建立SOCD預測模型，模型的前4個主成分變量可以解釋80%以上的光譜數據信息，貢獻率分別為47.36%、9.63%、16.18%和8.04%（表3），同時利用皮爾遜相關系數來驗證主成分變量與SOCD之間的關系，相關系數分別為0.688、0.310、0.402和0.284，值均滿足小于0.01，這說明光譜主成分變量與SOCD之間均表現出正相關的關系，且第一主成分（principal component1，PC1）與SOCD之間的相關性最高，第四主成分（principal component4，PC4）的相關性最低，這主要是由于不同的主成分變量包含不同的波段信息，而不同位置的波段信息對土壤中的不同組分具有不同程度的響應。由上節可知，基于光譜信息，利用S-G+1st+SNV預處理方法進行PLSR建模，能夠對SOCD進行較好的預測，標準差與預測均方根誤差比值RPD為1.523，2-Pred為0.605。

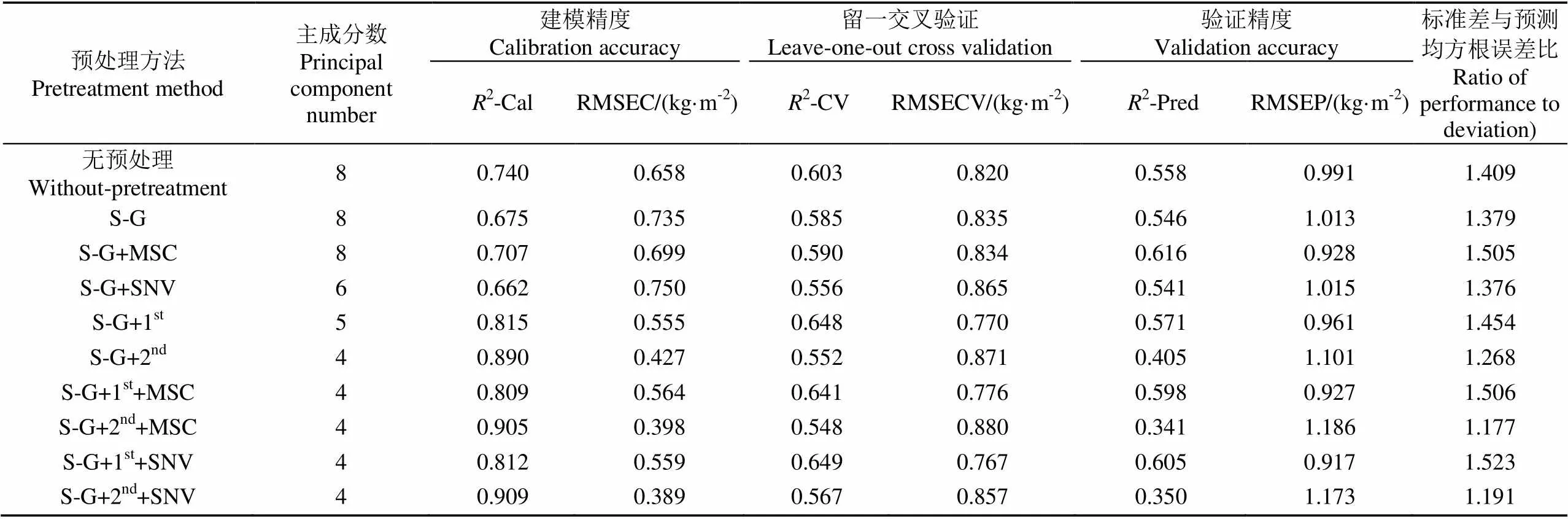
表2 基于不同預處理方法的PLSR模型及檢驗結果

注：S-G: Savitzky-Golay 平滑處理；1st、2nd：一階、二階微分處理；SNV：標準正態變換；MSC：多元散射校正處理；2-Cal：建模集決定系數；RMSEC：建模集均方根誤差；2-CV：留一交叉驗證決定系數；RMSECV：留一交叉驗證均方根誤差；2-Pred：驗證集決定系數；RMSEP：預測均方根誤差，下同。

Note: S-G: Savitzky-Golay smoothing; 1st, 2nd: first-order and second-order differential equation; SNV: standard normal variate; MSC: multiplicative seater correction;2-Cal:2of calibration; RMSEC: root mean squares error of calibration;2-CV:2of leave-one-out cross validation; RMSECV: root mean squares error of leave-one-out cross validation;R-Pred:2of prediction; RMSEP: root mean squares error of prediction, the same as below.

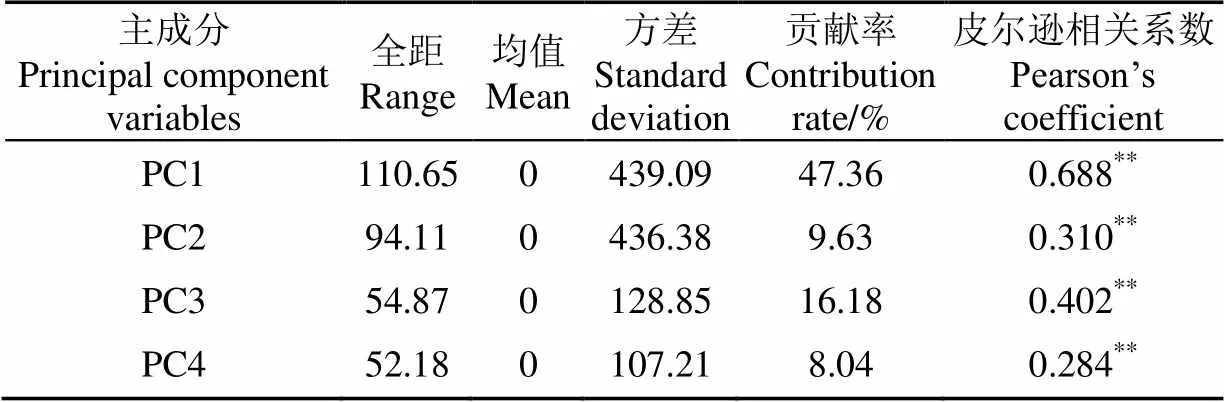
表3 樣本光譜信息主成分的基本統計

注：**為在0.01水平（雙側）上顯著。PC1、PC2、PC3、PC4分別為樣本光譜信息的第一、二、三、四主成分，下同。

Note: ** means significant at 0.01 level (double sides). PC1, PC2, PC3, PC4 represent the first, second, third, and the forth principal component of sample spectra, respectively, the same as below.

2.3.2 利用OK模型和COK模型構建SOCD預測模型

考慮土壤屬性具有空間變異性，對SOCD實測值進行普通克里格插值分析，其中半變異函數擬合模型采用指數函數，塊基比參數0/(0+)為59.32%，介于25%～75%之間，具有中等程度空間相關性[32]。驗證集決定系數2-Pred僅為0.004（表4），說明普通克里格模型對于SOCD預測結果精度并不理想。這主要是由于樣點布設時采用隨機布點法，未有SOCD的空間變異信息作為先驗知識，導致樣本密度不盡合理，進而影響OK模型的預測結果，普通克里格模型雖然考慮了變量的空間變異性，但對樣點本身數據質量依賴性較強。

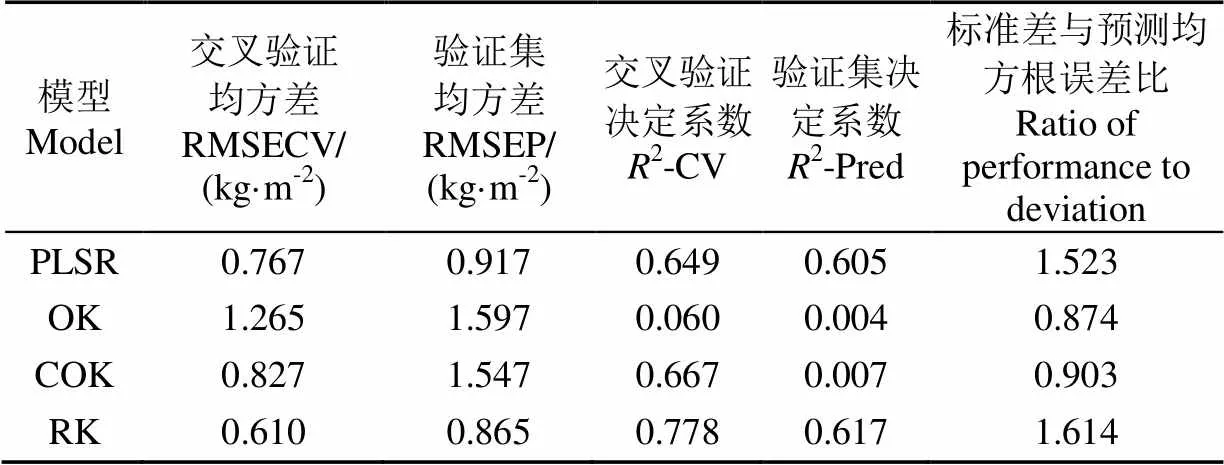
表4 PLSR、OK、COK及RK 4種方法的精度評價指標對比

注：PLSR：偏最小二乘回歸模型，OK：普通克里格模型，COK：協同克里格模型，RK：回歸克里格模型，下同。

Note: PLSR: partial least-squares regression model, OK: ordinary kriging model, COK: co-kriging model, RK: regression kriging model, the same as below.

根據光譜數據主成分與SOCD的皮爾遜相關系數，選取第一、二、三主成分作為輔助變量，以SOCD為主變量進行協同克里格插值，SOCD與各協同變量的半變異函數模型顯示，塊基比分別為34.20%、23.49%、37.09%（表5），第一、三輔助變量的塊基比介于25%～75%之間，具有中等程度空間相關性，第二輔助變量的塊基比小于25%，具有較強空間相關性[32]，交叉驗證決定系數為0.667（表4），建模集模型擬合度較好，這主要是由于土壤光譜反射率與SOCD相關性較強，可以提供有價值的輔助信息，在SOCD預測建模中起重要作用。但是由于COK模型對樣本密度均一性有一定要求，并且在模型預測過程中，未能結合預測集樣本光譜信息，致使預測精度不理想，2-Pred僅為0.007（表4）。

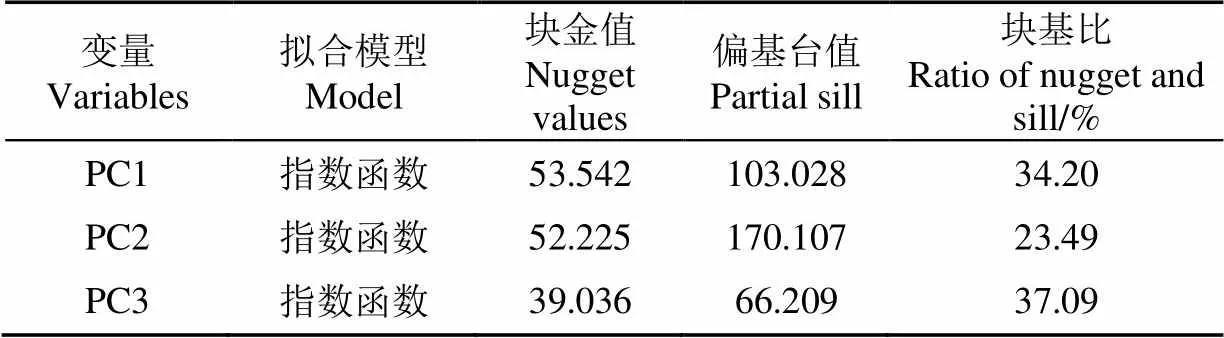
表5 協同克里格模型參數

2.3.3 利用RK模型構建SOCD預測模型

在利用RK模型構建SOCD預測模型的過程中，使用OLS得到模型殘差范圍為?1.29～1.24kg/m2，殘差值主要集中在0左右，偏度系數為?0.116，峰度系數為?0.369，通過Kolmogorov-Smirnov檢驗符合正態分布，適合進行克里格插值（圖3a）。對殘差進行普通克里格插值，半變異函數模型采用指數函數模型，塊基比為27.12%，接近25%，具有較高的空間相關性[32]（圖3b）。回歸克里格模型作為SOCD預測模型具有較高的驗證精度，2-Pred為0.617（表4）。土壤是變異性極強的連續體，空間非平穩性的存在導致OLS這一類全局模型無法捕捉到土壤變異的局部特征，利用克里格法對代表隨機性的殘差進行插值，插值結果能揭示可能被空間非平穩性所掩蓋的一些局部變化，反映出更加真實的土壤屬性空間變異情況。

2.4 驗證與評價SOCD預測模型

留一交叉驗證結果表明RK模型具有最好的建模精度，建立的模型能解釋建模集SOCD 77.8%的變異，而COK和PLSR次之，2-CV分別為0.667和0.649，OK模型最差，2-CV僅為0.06（表4）。OK模型的預測精度較差，這主要是由于樣點布設時采用隨機布點法，未有SOCD的空間變異信息作為先驗知識，導致樣本密度不盡合理，進而影響OK模型的預測結果；同時在小區域尺度中，受到土壤屬性空間復雜程度以及變程多樣性的影響，OK模型并不能保證半變異函數模型可以完全模擬真實的土壤屬性空間結構特征。光譜反射率作為土壤屬性的直接反應可以提供有價值的輔助信息來模擬SOCD的空間分布特征，在SOCD預測建模中起到重要的作用，這也是以土壤光譜反射率為自變量的PLSR模型和以土壤光譜反射率為輔助變量的COK模型在預測精度方面優于OK模型的主要原因。對于多元線性回歸模型而言，一旦預測殘差具有空間結構，就說明因變量的部分變異未能被模型所解釋，為此本研究選用RK模型來減少殘差結構對于預測結果的影響。結果表明RK模型具有相對較高的預測精度，這也體現了在建立土壤屬性多元線性回歸模型時考慮殘差空間特征的必要性。

3 討 論

土壤有機碳儲量與氣候、成土母質、土壤生物、地形、成土時間等環境因素以及人類活動密切相關，土壤有機碳具有空間依賴性和空間異質性，進而導致土壤有機碳空間分布的不確定性，影響土壤有機碳密度計算和土壤有機碳儲量估算的精度。

土壤光譜是與SOCD相關的土壤內在組分與外部因素的代理變量，光譜反射率可以直接反映土壤的物理結構及化學特征，光譜反射率也可以通過某一波段的光譜特征來反映相對應的SOCD。文中考慮到土壤光譜信息進行建模，相比于OK模型，以土壤光譜反射率為自變量的PLSR模型和以土壤光譜反射率為輔助變量的COK模型預測效果更好，并且與前人的研究結果相一致[19]，說明借助于光譜反射率作為輔助信息在一定程度上可以提高模型的預測精度，光譜反射率在土壤屬性預測建模中起重要作用。

土壤本身是一個開放的復雜系統，由于受復雜的成土過程、自然環境要素以及人類活動等因素的影響，在不同的地區SOCD存在各具特點的空間分異規律，表現出一定的空間異質性。結合光譜信息和SOCD的空間分布信息構建的COK模型，建模集的2-CV為0.667，高于僅考慮光譜信息進行建模的PLSR模型（2-CV=0.649），說明SOCD的空間信息可以提高模型的建模精度，但是由于克里格模型是借助于半變異函數的權重系數而建立的空間插值模型，在地形復雜或者屬性變化強烈的區域難以進行準確的預測，并且會忽略外界影響因素對土壤屬性的影響和作用，因而本研究中的COK模型的預測精度低于PLSR模型。

由于預測殘差空間自相關性的存在，難以保證通過PLSR模型得到的預測結果具有無偏性和獨立性，為此考慮在構建基于光譜的土壤屬性預測模型時，盡量地減少殘差對結果的影響，有助于模型精度的提高。文中RK模型的建模精度（2-CV=0.778）和預測精度（2-Pred=0.617）均高于PLSR模型（2-CV=0.649，2-Pred=0.605），說明同時考慮光譜反射率和土壤屬性的空間特性可以提高預測精度，考慮多元線性回歸模型殘差的空間結構能夠更加真實的反映出土壤屬性的空間變異情況。

研究表明，PLSR模型預測效果（2-Pred=0.605）優于OK模型（2-Pred=0.004），這兩種模型均可以低成本地預測土壤屬性，但是都具有一定的缺點，OK模型是一種基于樣點空間依賴性的局部預測方法，PLSR模型雖可以進行大尺度全局預測，但是精準的預測結果需要以土壤變量具有較寬的測定范圍值以及變量與土壤反射光譜具有直接相關性為前提，具有一定的局限性。克里格法的前提是假設數據來自平穩的隨機過程，然而研究區域具有特殊性，受人為活動的影響，SOCD的分布并非隨機過程，因此OK和COK模型未能很好的預測結果，PLSR和RK模型則充分利用了未知樣點的光譜這一獲取便捷的先驗信息，因此對未知樣點的SOCD估算效果較好。光譜反射率作為COK和RK模型中重要的輔助變量，光譜數據的預處理過程對土壤屬性的預測結果有極大的影響，之后的研究需要進行更多的實驗來選出最佳預處理方法。

此外，本文對SOCD進行估測時，沒有對不同土地利用類型的土壤進行區分，只是根據各種地類的面積，確定不同地類上采樣點的個數以確保樣本集的全面性與準確性，而不同地類對應不同的土壤類型，也意味著不同的SOCD值，以后的研究可以進一步探索SOCD在不同地類上的分布規律。

4 結 論

本文借助于土壤可見—近紅外反射光譜（400～2 350 nm），構建了偏最小二乘回歸、普通克里格、協同克里格、回歸克里格模型，進行土壤有機碳密度預測精度對比分析。考慮了光譜反射率的空間結構特征，以及多元線性回歸模型殘差的空間結構，從不同的角度和方向來盡可能的提高空間模型的預測精度和準確度，得出以下結論：

1）偏最小二乘回歸模型（partial least squares regression，PLSR）中光譜數據預處理采用平滑處理、一階微分和標準正態變換的組合時結果最佳，留一交叉驗證決定系數（2of leave-one-out cross validation，2-CV）值為0.649，模型的標準差與預測均方根誤差比（ratio of performance to deviation，RPD）值為1.523，均達到最高值，優于其他預處理方法。

2）當選用光譜反射率作為協同克里格模型（co-kriging，COK）的輔助變量時，在一定程度上可以提高模型的建模精度。同時考慮多元線性回歸模型殘差的空間特征，對提高模型的預測精度也起到重要的作用，因此，回歸克里格模型（regression kriging，RK）具有最高的預測精度（2-Pred=0.617）。

[1] 潘根興，趙其國. 我國農田土壤碳庫演變研究：全球變化和國家糧食安全[J]. 地球科學進展，2005，20(4)：384－393. Pan Genxing, Zhao qiguo. Study on evolution of organic carbon stock in agricultural soils of China: Facing the challenge of global chance and food security[J]. Advances in Earth Science, 2005, 20(4): 384－393. (in Chinese with English abstract)

[2] 盧延年，劉艷芳，陳奕云，等. 江漢平原土壤有機碳含量高光譜預測模型優選[J]. 中國農學通報，2014，30(26)：127－133. Lu Yannian, Liu Yanfang, Chen Yiyun, et al. Optimization of the hyperspectral prediction model of soil organic carbon contents of Jianghan plain[J]. Chinese Agricultural Science Bulletin, 2014, 30(26): 127－133. (in Chinese with English abstract)

[3] 王紹強，周成虎. 中國陸地土壤有機碳庫的估算[J]. 地理研究，1999，18(4)：349－356. Wang Shaoqiang, Zhou Chenghu. Estimating soil carbon reservior of terrestrial ecosystem in China[J]. Geographical Research, 1999, 18(4): 349－356. (in Chinese with English abstract)

[4] 張小超，吳靜珠，徐云. 近紅外光譜分析技術及其在現代農業中的應用[M]. 北京：電子工業出版社，2012：95－140.

[5] 陳濤，常慶瑞，劉京. 基于光譜信息輔助的污灌區農田土壤鎘協同克里格分析[J]. 光譜學與光譜分析，2013，33(8)：2157－2162. Chen Tao, Chang Qingrui, Liu Jing. Study of spatial interpolation of soil Cd contents in sewage irrigated area based on soil spectral information assistance[J]. Spectroscopy and Spectral Analysis, 2013, 33(8): 2157－2162. (in Chinese with English abstract)

[6] 李耀翔，汪洪濤，耿志偉，等. 基于近紅外光譜及BP神經網絡分析法預測森林土壤有機碳含量[J]. 西部林業科學，2014，43(3)：1－6. Li Yaoxiang, Wang Hongtao, Geng Zhiwei, et al. Prediction of forest soil organic carbon content based on NIRS and BP neural network[J]. Journal of West China Forestry Science, 2014, 43(3): 1－6. (in Chinese with English abstract)

[7] 李耀翔，汪洪濤，耿志偉，等. 基于NIR及PLS-PCR-SVR預測森林土壤有機碳含量[J]. 安徽農業科學，2014，42(15)：4702－4706. Li Yaoxiang, Wang Hongtao, Geng Zhiwei, et al. Prediction of forest soil carbon content based on the near infrared spectroscopy and PLS-PCR-SVR[J]. Journal of Anhui Agricultural Sciences, 2014, 42(15): 4702－4706. (in Chinese with English abstract)

[8] 王紹強，劉紀遠，于貴瑞. 中國陸地土壤有機碳蓄積量估算誤差分析[J]. 應用生態學報，2003，14(5)：797－802. Wang Shaoqiang, Liu Jiyuan, Yu Guirui. Error analysis of estimating terrestrial soil organic carbon storage in China[J]. Chinese Journal of Applied Ecology, 2003, 14(5): 797－802. (in Chinese with English abstract)

[9] 邵月紅，潘劍君，許信旺，等. 淺談土壤有機碳密度及儲量的估算方法[J]. 土壤通報，2006，37(5)：1007－1011. Shao Yuehong, Pan Jianjun, Xu Xinwang, et al. Discussion on the methods for estimating soil organic carbon density and storage[J]. Chinese Journal of Soil Science, 2006, 37(5): 1007－1011. (in Chinese with English abstract)

[10] 吳瑾，吳克寧，趙華甫，等. 土壤有機碳儲量估算方法及土地利用調控措施研究進展[J]. 中國土地科學，2010，24(10)：18－24. Wu Jin, Wu Kening, Zhao Huafu, et al. Review on the methods of soil organic carbon storage estimation and land use control measures[J]. China Land Science, 2010, 24(10): 18－24. (in Chinese with English abstract)

[11] 顧成軍. 克里格插值在區域土壤有機碳空間預測中的應用[J]. 中國土壤與肥料，2014(3)：93－97. Gu Chengjun. Application of kriging method in spatial prediction of regional soil organic carbon[J]. Soil and Fertilizer Sciences in China, 2014(3): 93－97. (in Chinese with English abstract)

[12] 郭龍，張海濤，陳家贏，等. 基于協同克里格插值和地理加權回歸模型的土壤屬性空間預測比較[J]. 土壤學報，2012，49(5)：1037－1042. Guo Long, Zhang Haitao, Chen Jiaying, et al. Comparison between co-kriging model and geographically weighted regression model in spatial prediction of soil attributes[J]. Acta Pedologica Sinica, 2012, 49(5): 1037－1042. (in Chinese with English abstract)

[13] 楊順華，張海濤，郭龍，等. 基于回歸和地理加權回歸Kriging的土壤有機質空間插值[J]. 應用生態學報，2015，26(6)：1649－1656. Yang Shunhua, Zhang Haitao, Guo Long, et al. Spatial interpolation of soil organic matter using regression kriging and geographically weighted regression kriging[J]. Chinese Journal of Applied Ecology, 2015, 26(6): 1649－1656. (in Chinese with English abstract)

[14] 姜勇，梁文舉，李琪. 利用與回歸模型相結合的克里格方法對農田土壤有機碳的估值及制圖[J]. 水土保持學報，2005，19(5)：99－102. Jiang Yong, Liang Wenju, Li Qi. Prediction and Mapping of Soil Organic Carbon in Farmland Using Kriging Combined with Regression[J]. Journal of Soil and Water Conservation, 2005, 19(5): 99－102. (in Chinese with English abstract)

[15] 代富強，周啟剛，劉剛才. 基于回歸克里格和遙感的紫色土區土壤有機質含量空間預測[J]. 土壤通報，2014，45(3)：562－567. Dai Fuqiang, Zhou Qigang, Liu Gangcai. Spatial prediction of soil organic matter contents in a purplish soil region with regression Kriging and remote sensing[J]. Chinese Journal of Soil Science, 2014, 45(3): 562－567. (in Chinese with English abstract)

[16] 張忠啟，于法展. 土壤類型信息在土壤有機碳空間預測中的應用研究[J]. 中國農學通報，2013，29(11)：139－144. Zhang Zhongqi, Yu Fazhan. Study on the application of soil type information in spatial prediction of soil organic carbon[J]. Chinese Agricultural Science Bulletin, 2013, 29(11): 139－144. (in Chinese with English abstract)

[17] 鄧祥征，姜群鷗，林英志，等. 中國農田土壤有機碳貯量變化預測[J]. 地理研究，2010，29(1)：93－101. Deng Xiangzheng, Jiang Qunou, Lin Yingzhi, et al. Simulation of the changes of soil organic carbon stock of cropland in China[J]. Geographical Research, 2010, 29(1): 93－101. (in Chinese with English abstract)

[18] Ge Y, Thomasson J A, Morgan C L, et al. VNIR diffuse reflectance spectroscopy for agricultural soil property determination based on regression-kriging[J]. Transactions of the ASABE, 2007, 50(3): 1081－1092.

[19] Bilgili A V, Akbas F, Es H M V. Combined use of hyperspectral VNIR reflectance spectroscopy and kriging to predict soil variables spatially[J]. Precision Agriculture, 2011, 12(3): 395－420.

[20] Liu Yaolin, Guo Long, Jiang Qinghu, et al. Comparing geospatial techniques to predict SOC stocks[J]. Soil & Tillage Research, 2015(148): 46－58.

[21] 梁重山，黨志，劉叢強. 土壤沉積物樣品中有機碳含量的快速測定[J]. 土壤學報，2002，39(1)：129－133. Liang Chongshan, Dang Zhi, Liu Congqiang. Rapid determination of total organic carbon in soil/sediment samples[J]. Acta Pedologica Sinica, 2002, 39(1): 129－133. (in Chinese with English abstract)

[22] 陳奕云，漆錕，劉耀林，等. 顧及土壤濕度的土壤有機質高光譜預測模型傳遞研究[J]. 光譜學與光譜分析，2015，35(6)：1705－1708.

Chen Yiyun, Qi Kun, Liu Yaolin, et al. Transferability of Hyperspectral Model for Estimating Soil Organic Matter Concerned with Soil Moisture[J]. Spectroscopy and Spectral Analysis.2015, 35(6): 1705－1708. (in Chinese with English abstract)

[23] Shi Tiezhu, Chen Yiyun, Liu Yaolin, et al. Visible and near-infrared reflectance spectroscopy—An alternative for monitoring soil contamination by heavy metals[J]. Journal of Hazardous Materials, 2014, 265(2): 166－176.

[24] Rinnan A, Berg F V D, Engelsen S B. Review of the most common pre-processing techniques for near-infrared spectra[J]. Trac-Trends in Analytical Chemistry, 2009, 28(10): 1201－1222.

[25] Liu Yaolin, Chen Yiyun. Estimation of total iron content in floodplain soils using VNIR spectroscopy—a case study in the Le’an River floodplain, China[J]. International Journal of Remote Sensing, 2012, 33(18): 5954－5972.

[26] Wold S , Kettaneh-Wold N , Skagerberg B. Nonlinear PLS modeling[J]. Chemometrics and Intelligent Laboratory Systems, 1989, 7(1/2): 53－65.

[27] Haaland D M, Thomas E V. Partial least-squares methods for spectral analyses. 1. Relation to other quantitative calibration methods and the extraction of qualitative information[J]. Analytical Chemistry, 1988, 60(11): 1193－1202.

[28] Kennard R W, Stone L A. Computer aided design of experiments[J]. Technometrics, 1969, 11(1): 137－148.

[29] 劉艷芳，盧延年，郭龍，等. 基于地類分層的土壤有機質光譜反演校正樣本集的構建[J]. 土壤學報，2016，53(2)：332－341.

Liu Yanfang, Lu Yannian, Guo Long, et al. Construction of calibration set based on the land use types in visible and Near-InfRared (VIS-NIR) model for soil organic matter estimation[J]. Acta Pedologica Sinica, 2016, 53(2): 332－341. (in Chinese with English abstract)

[30] 于雷，洪永勝，耿雷，等. 基于偏最小二乘回歸的土壤有機質含量高光譜估算[J]. 農業工程學報，2015，31(14)：103－109.

Yu Lei, Hong Yongsheng, Geng Lei, et al. Hyperspectral estimation of soil organic matter content based on partial least squares regression[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(14): 103－109. (in Chinese with English abstract)

[31] Shi Tiezhu, Cui Lijuan, Wang Junjie, et al. Comparison of multivariate methods for estimating soil total nitrogen with visible/near-infrared spectroscopy[J]. Plant and Soil, 2013, 366(1): 363－375.

[32] Johnson R A, Wichern D W. Applied multivariate statistical analysis[M]. New Jersey: Prentice Hall, 2002: 425－430.

Geostatistical models of soil organic carbon density prediction based on soil hyperspectral reflectance

Liu Yanfang1,2,3, Song Yuling1,2,3, Guo Long4, Chen Yiyun1,2,5,6※, Lu Yannian1,2,3, Liu Yi1,2,3

(1.430079; 2.430079; 3.,,,430079,; 4.,,430070,; 5.,430079,; 6.,215123,)

The availability of soil organic carbon density (SOCD) information is of great importance for the development of ecological agriculture and the study of global climate change. Compared with traditional laboratory analysis, Visible and near-infrared (VNIR) reflectance spectroscopy has proven to be a rapid, non-destructive and cost effective method for estimating a variety of soil properties. It has got rapid development and has been applied in the field of soil research. In the prediction of soil properties by using spectral information, however, traditional linear regression models often ignore the spatial heterogeneity and dependency of soil, and fail to consider the spatial structure of the error term. With the aims to fill the current gap, a total of 232 topsoil samples were collected in Jianghan Plain with their spectral reflectance and SOCD measured. Partial least squares regression (PLSR), ordinary kriging (OK), co-kriging (COK), and regression kriging (RK) were used to estimate SOCD by using differently pre-treated spectral reflectance. Due to the facts that spectral pretreatments are crucial to reduce the physical variability and particle size effect, and are helpful to remove both additive and multiplicative effects in the spectra, five combinations of spectral pretreatments were utilized while predicting SOCD with PLSR. They were Savitzky-Golay smoothing (S-G), S-G + Multiplicative Scatter Correction (MSC), S-G+Standard Normal Variate (SNV), S-G + first derivative (1st), S-G + second derivative (2nd), S-G+1st+MSC, S-G+2nd+MSC, S-G+1st+SNV, S-G+2nd+SNV. The prediction capabilities of the models were evaluated byR, root mean squared error (RMSE), and ratio of performance to deviation (RPD). Results showed that the RK approach which utilized soil spectra information outperformed the others, with the highestR-Pred 0.617 and RPD 1.614, and the lowest RMSEP 0.865 kg/m2. PLSR took the second place withR-Pred 0.605, RPD 1.523 and RMSEP 0.917 kg/m2, which was also acceptable for SOCD prediction. COK and OK generally failed in the predictions of SOCD, withR-Pred equaled to 0.007 and 0.004, RPD equaled to 0.903 and 0.874 and RMSEP equaled to 1.547 and 1.597 kg/m2, respectively. Results indicated that the RK model, which considered both the spectral reflectance and the spatial structure of the error term of multivariate linear regression model can improve the prediction accuracy of SOCD. The fundamental reasons could be that soil spectra are comprehensive reflections of soil properties and those environmental factors that influence the formation of soil. Therefore, soil spectra are related with the variation of SOCD, and could be helpful in the prediction of SOCD. Besides, the optimal spectral pretreatment for PLSR modelling of SOCD is the combination of smoothing, first-order derivation and SNV. In summary, soil reflectance spectra in the visible and near-infrared region (350-2 500 nm) could serve as an effective proxy variable for SOCD estimation. Given that soil VNIR reflectance spectra are easy and quick to measure, and the measurement is also environmentally friendly, we would like to argue that soil spectral reflectance could serve as an ideal auxiliary variable for the spatial interpolation of SOCD.

soils; models; spectrum analysis; soil organic carbon density; partial least-squares regression; co-kriging; regression kriging

10.11975/j.issn.1002-6819.2017.02.025

S151.9+5

A

1002-6819(2017)-02-0183-09

2016-05-10

2016-10-22

國家自然科學基金項目（41501444）；蘇州市應用基礎農業項目（SYN201422）；中央大學基礎研究基金（2662016QD032）

劉艷芳，女，湖北武漢人，教授，博士，主要從事區域規劃和經濟地理研究及地理信息應用工程的研究工作。武漢 武漢大學資源與環境科學學院，430079。Email：yfliu610@163.com

陳奕云，男，福建泉州人，副教授，研究方向為土壤遙感與地理信息科學。武漢 武漢大學資源與環境科學學院，430079。 Email：chenyy@whu.edu.cn

劉艷芳，宋玉玲，郭 龍，陳奕云，盧延年，劉 以. 結合高光譜信息的土壤有機碳密度地統計模型[J]. 農業工程學報，2017，33(2)：183－191. doi：10.11975/j.issn.1002-6819.2017.02.025 http://www.tcsae.org

Liu Yanfang, Song Yuling, Guo Long, Chen Yiyun, Lu Yannian, Liu Yi. Geostatistical models of soil organic carbon density prediction based on soil hyperspectral reflectance[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(2): 183－191. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.02.025 http://www.tcsae.org