一種改進(jìn)的Inter-Apriori算法①
崔雙彌, 張德生
?
一種改進(jìn)的Inter-Apriori算法①
崔雙彌, 張德生
(西安理工大學(xué)理學(xué)院, 西安 710054)
建立了一種基于定位和權(quán)值事務(wù)項(xiàng)集的挖掘算法, 該算法只需掃描一遍事務(wù)數(shù)據(jù)庫. 利用垂直型布爾矩陣來存儲(chǔ)交易數(shù)據(jù), 通過 “與”運(yùn)算與權(quán)值來計(jì)算計(jì)算支持度, 利用定位搜索和合并事務(wù)矩陣相同列來剪枝, 從而減少了算法在挖掘過程中使用的存儲(chǔ)空間和計(jì)算時(shí)間. 實(shí)驗(yàn)結(jié)果表明, 改進(jìn)算法在性能上得到了的明顯提高.
頻繁項(xiàng)集; 垂直型布爾矩陣; Inter-Apriori算法
1 引言
關(guān)聯(lián)規(guī)則挖掘[1]是數(shù)據(jù)挖掘領(lǐng)域的一個(gè)重要問題, 旨在發(fā)現(xiàn)大量數(shù)據(jù)中項(xiàng)集之間有趣的關(guān)聯(lián)或相關(guān)聯(lián)系. 這些關(guān)聯(lián)關(guān)系可以為商業(yè)決策者提供有價(jià)值的信息, 從而實(shí)現(xiàn)商務(wù)決策的制定, 如交叉銷售、商品擺放等.
Apriori算法[2]是挖掘關(guān)聯(lián)規(guī)則最經(jīng)典的算法, 它在執(zhí)行“連接-剪枝”的過程中采用逐層搜索的迭代方法來挖掘滿足閾值的關(guān)聯(lián)規(guī)則, 但存在兩個(gè)缺陷: (1)重復(fù)多次掃描事務(wù)數(shù)據(jù)庫; (2)產(chǎn)生的候選集數(shù)據(jù)過大.
近年來, 基于矩陣的關(guān)聯(lián)規(guī)則挖掘算法研究快速發(fā)展, 使得挖掘效率進(jìn)一步提高. 如基于壓縮矩陣的研究方法[3,4]、基于矩陣分解的研究方法[5]、基于上三角矩陣的研究方法[6]、基于排序索引矩陣的研究方法[7],基于矩陣和數(shù)組的研究方法[9,10]等,文獻(xiàn)[11]提出了基于矩陣取交集的Inter-Apriori算法, 但當(dāng)Tidset的規(guī)模龐大時(shí)將出現(xiàn)以下問題: (1)求Tidset的交集的操作將消耗大量時(shí)間,影響了算法的效率; (2)Tidset的規(guī)模相當(dāng)龐大, 消耗系統(tǒng)大量的內(nèi)存. 文獻(xiàn)[12]提出對(duì)項(xiàng)集矩陣進(jìn)行累加運(yùn)算, 雖能大大提高挖掘效率, 但只適用于事務(wù)數(shù)據(jù)庫中, 重復(fù)事務(wù)多的情形. 文獻(xiàn)[13]提出了基于散列布爾矩陣的研究方法, 雖然大大減少了算法的比較次數(shù), 提高了算法效率, 但卻增加了算法的空間復(fù)雜度, 加大了開銷.
針對(duì)以上問題, 本文建立了一種基于垂直型布爾矩陣的挖掘關(guān)聯(lián)規(guī)則頻繁項(xiàng)目的算法, 該算法將事務(wù)數(shù)據(jù)庫映射為垂直型布爾矩陣, 在此基礎(chǔ)上進(jìn)行挖掘頻繁項(xiàng)集, 很大程度上減少了時(shí)間和空間消耗.
2 Inter-Apriori算法的改進(jìn)
2.1 建立垂直型布爾矩陣
定義1. 項(xiàng)集I(itemset)[14]: 事務(wù)數(shù)據(jù)庫中個(gè)不同項(xiàng)目組成的集合, 記作, 其中的每個(gè)項(xiàng)目相當(dāng)于一種商品.
定義2. 設(shè)有項(xiàng)目, 包含項(xiàng)目的所有事務(wù)的標(biāo)識(shí)符的集合稱為項(xiàng)目的Tidset. 在這種數(shù)據(jù)表示方法中, 數(shù)據(jù)庫的事務(wù)由項(xiàng)目和該項(xiàng)目的Tidset組成, 該事務(wù)有項(xiàng)目唯一標(biāo)識(shí).
定義3.垂直型布爾矩陣
對(duì)于任意給定的事務(wù)數(shù)據(jù)庫, 令:
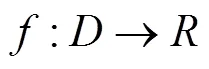
因此, 事務(wù)數(shù)據(jù)庫經(jīng)過一次掃描后, 就經(jīng)上述定義映射為垂直型布爾矩陣.
2.2 支持計(jì)數(shù)計(jì)算
若項(xiàng)集的出現(xiàn)頻率大于或等于min-sup與中事務(wù)總數(shù)的乘積, 稱項(xiàng)集滿足最小支持度min-sup, 若項(xiàng)集滿足最小支持度, 則稱為頻繁項(xiàng)集集. 頻繁-項(xiàng)集通常記作L.
支持計(jì)數(shù)通過兩個(gè)項(xiàng)集的Tidset的“與”運(yùn)算后得的矩陣與權(quán)重的乘積得到, 因此關(guān)聯(lián)規(guī)則的支持計(jì)數(shù)定義為:
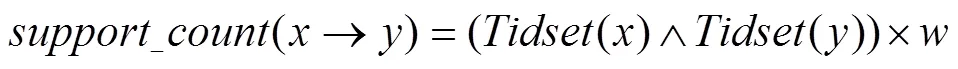
性質(zhì)1: 頻繁項(xiàng)集的所有非空子集都必須是頻繁的.
性質(zhì)2: 在數(shù)據(jù)庫中若有一事務(wù)T其長度小于+1, 則由項(xiàng)集生成+1項(xiàng)頻繁項(xiàng)集事務(wù)T是沒有必要掃描的.
性質(zhì)3: 由-1項(xiàng)集生成項(xiàng)集時(shí), 當(dāng)作自身連接時(shí), 若兩個(gè)項(xiàng)集的前-2項(xiàng)不同, 則放棄連接運(yùn)算, 因?yàn)楫a(chǎn)生的項(xiàng)集不是重復(fù)的就是非頻繁項(xiàng)集.
2.3 改進(jìn)Inter-Apriori算法的主要思想
(1) 頻繁1-項(xiàng)集. 掃描事務(wù)數(shù)據(jù)庫一次, 將事務(wù)數(shù)據(jù)庫利用定義1映射為垂直型布爾矩陣, 同時(shí)在矩陣前加一行全為1的權(quán)值; 矩陣后加一列count記錄該商品出現(xiàn)次數(shù),加一行sum-c, 記錄每個(gè)事務(wù)所包含的項(xiàng)目數(shù). 把不滿足最小支持度的行(count列中min-sup所在的行)刪去, 得到矩陣(布爾矩陣和sum-c行), 得到頻繁1-項(xiàng)集.
(2) 剪枝. 首先, 合并矩陣中相同列, 即對(duì)整個(gè)矩陣中相同列進(jìn)行整體合并, 得出合并后的矩陣及合并后的相同列所在的位置, 根據(jù)位置對(duì)矩陣應(yīng)列的權(quán)值累加; 其次. 查找sum-c行大于或等于的位置, 把小于的列刪去, 得到無重復(fù)列且每個(gè)事務(wù)所包含的項(xiàng)目數(shù)大于或等于的矩陣D.
(3) 頻繁項(xiàng)集挖掘, 由-1項(xiàng)集挖掘-項(xiàng)集, 按照性質(zhì)3進(jìn)行連接. 對(duì)應(yīng)的行進(jìn)行“與”運(yùn)算, 利用定義4計(jì)算支持計(jì)數(shù). 重復(fù)過程2,3直至生成的頻繁項(xiàng)集為空.
2.4 改進(jìn)的Inter-Apriori算法
輸入: 事務(wù)數(shù)據(jù)庫; 最小支持度min-sup
2.5 實(shí)例分析
假定最小支持計(jì)數(shù)為2, 表1記錄了9個(gè)顧客購買5種商品的具體情況.

表1 事務(wù)數(shù)據(jù)庫
(1) 事務(wù)數(shù)據(jù)庫映射為垂直型布爾矩陣, 并計(jì)算每個(gè)項(xiàng)的支持?jǐn)?shù)count, 在矩陣的第一行給每個(gè)項(xiàng)集賦權(quán)值, 并在矩陣的最后一列sum-c, 記錄每個(gè)事務(wù)所包含的項(xiàng)目總數(shù). 如表2所示.
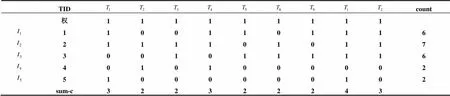
表2 垂直型布爾矩陣
(2) 掃描表2, 把不滿足最小支持度的行(count列中min-sup所在的行)刪去, 得到頻繁1-項(xiàng)集, 并合并相同的列, 相應(yīng)改變權(quán)值. 得到頻繁1-項(xiàng)集,如表3所示
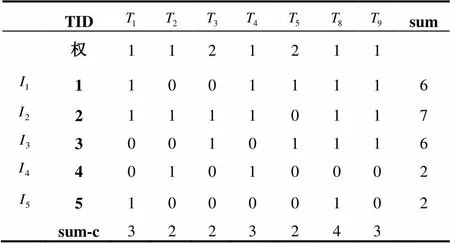
表3 頻繁1-項(xiàng)集
(3) 描表3, 進(jìn)行連接, 并且相應(yīng)的列進(jìn)行“與”運(yùn)算, 如項(xiàng)集,, 支持計(jì)數(shù)為, 因此是頻繁2-項(xiàng)集. 如表4所示.
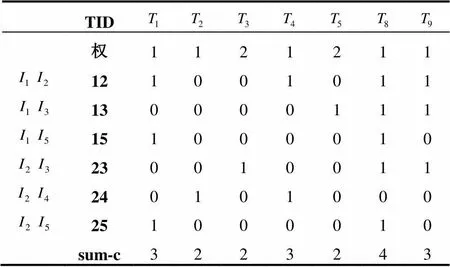
表4 頻繁2-項(xiàng)集
(4) 合并頻繁2-項(xiàng)集矩陣中相同的列, 查找sum-c行大于或等于3的位置, 刪去不符合條件對(duì)應(yīng)的列. 得到剪枝后的頻繁2-項(xiàng)集, 為挖掘頻繁3-項(xiàng)集減少了計(jì)算量. 如表5所示.
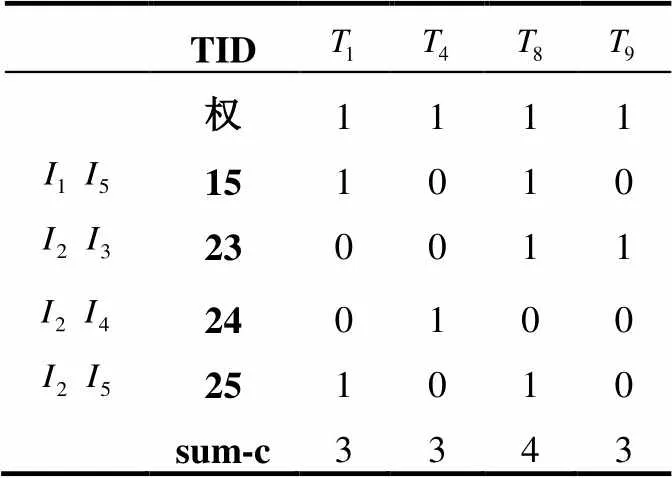
表5 剪枝后頻繁2-項(xiàng)集
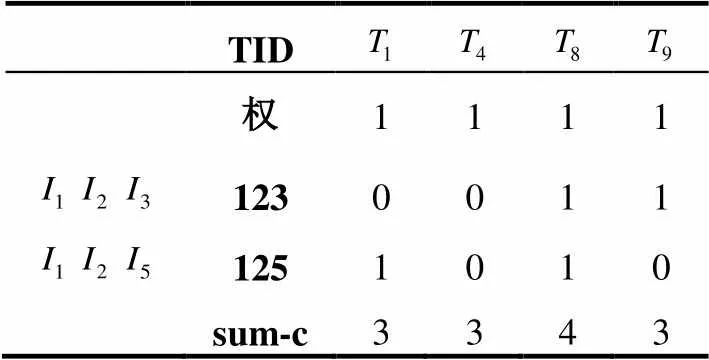
表6 頻繁3-項(xiàng)集
(6)利用上述⑷的步驟, 整理頻繁3-項(xiàng)集后得到剪枝后頻繁3-項(xiàng)集, 因?yàn)橹许?xiàng)集的個(gè)數(shù)為2<4, 所以算法終止. 如表7所示.

表7 剪枝后頻繁3-項(xiàng)集
3 改進(jìn)算法的性能分析
Inter-Apriori算法和改進(jìn)的算法都將事務(wù)數(shù)據(jù)庫映射為垂直型矩陣, 實(shí)現(xiàn)了僅掃描一次數(shù)據(jù)庫; 其次, 由-1-項(xiàng)集連接生成-項(xiàng)集時(shí), 若滿足兩個(gè)項(xiàng)集的前項(xiàng)不同, 則放棄連接運(yùn)算, 避免產(chǎn)生過多的候選項(xiàng)集, 同時(shí)減少了掃描項(xiàng)集的次數(shù), 有效的提高了算法的挖掘效率.
Inter-Apriori算法和本文算法的不同主要有:
(1)在空間復(fù)雜性上: Inter-Apriori算法將產(chǎn)生的項(xiàng)集存儲(chǔ)在內(nèi)存中, 而本文算法利用布爾矩陣進(jìn)行存儲(chǔ), 記錄樣本占用更少的空間; 同時(shí), 利用性質(zhì)2和性質(zhì)3對(duì)候選項(xiàng)集進(jìn)行剪枝縮小了原布爾矩陣的規(guī)模, 也將占用更少的存儲(chǔ)空間.
同時(shí), Inter-Apriori算法是利用Tidset集取交集, 而本文算法對(duì)布爾矩陣進(jìn)行“與”運(yùn)算, 效率較高.
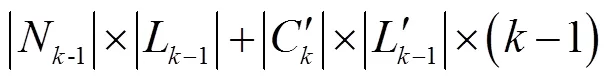
而Inter-Apriori算法利用性質(zhì)3的計(jì)算量為:
3.1 實(shí)驗(yàn)環(huán)境
為了驗(yàn)證本算法的性能, 將其與Inter-Apriori算法作對(duì)比. 實(shí)現(xiàn)環(huán)境: 7GHZCPU, 2G內(nèi)存和Windows XP操作系統(tǒng), 程序用matlab語言實(shí)現(xiàn). 實(shí)驗(yàn)數(shù)據(jù)集[15]來自IBM Almaden實(shí)驗(yàn)室生成的T10I4D100K和UCI機(jī)器學(xué)習(xí)數(shù)據(jù)倉庫, 選擇大小不同的四個(gè)事務(wù)數(shù)據(jù)集, 分別為兩個(gè)稠密的Mushroom、Chess和兩個(gè)稀疏的Nursery、T10I4D100K(取前22000個(gè)項(xiàng)目), 如表8所示.
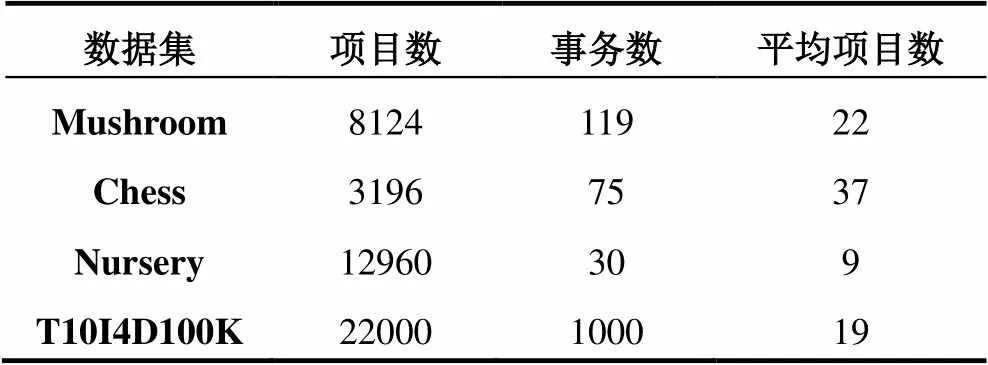
表8 四種數(shù)據(jù)集
3.2 實(shí)驗(yàn)結(jié)果
根據(jù)數(shù)據(jù)集的稠密性, 不同的數(shù)據(jù)集給定不同的支持度, 然后分別測(cè)試挖掘頻繁項(xiàng)集所消耗的時(shí)間和空間, 四種數(shù)據(jù)集的測(cè)試情況如圖1.
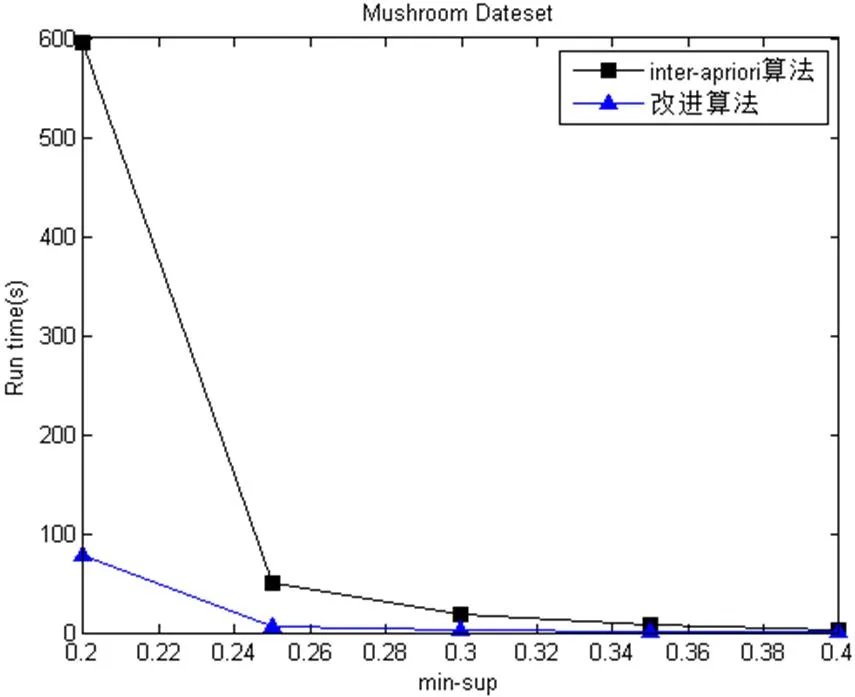
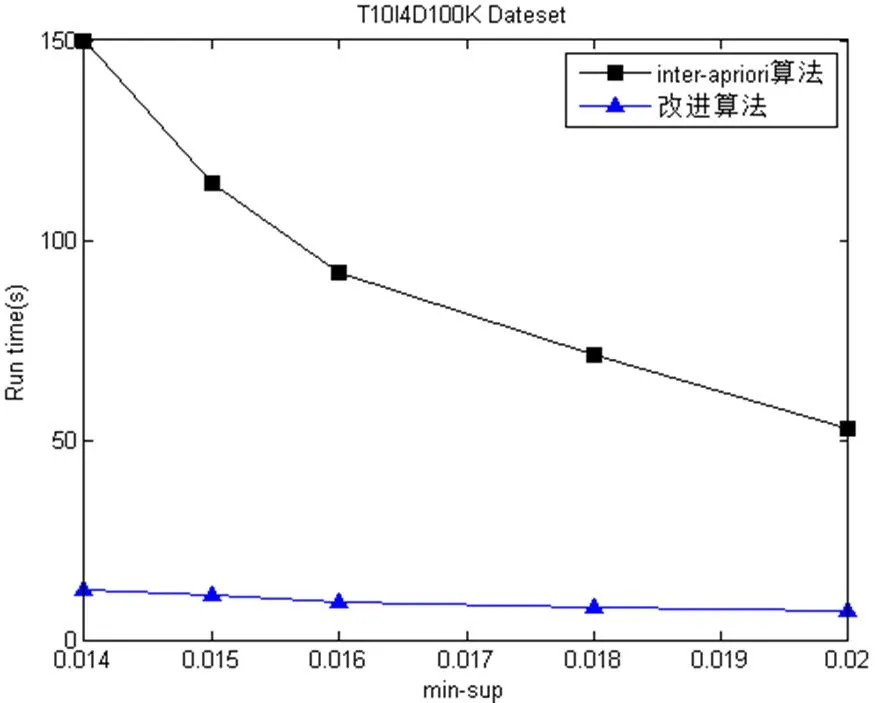
圖1 四種數(shù)據(jù)的運(yùn)行時(shí)間
從時(shí)間復(fù)雜度上看, 改進(jìn)的算法時(shí)間消耗比Inter-Apriori算法較少, 性能優(yōu)勢(shì)比較明顯, 同時(shí), 時(shí)間復(fù)雜度也明顯降低了. 因?yàn)橹С侄仍酱髸r(shí), 產(chǎn)生的頻繁項(xiàng)集越少. 在支持度較小的情況下, 對(duì)于密集型數(shù)據(jù)集Mushroom與Chess, 改進(jìn)后的算法運(yùn)行時(shí)間變化緩慢, 而Inter-Apriori算法的變化趨勢(shì)較大. 但是對(duì)于稀疏型數(shù)據(jù)集Nursery與T10I4D100K, 隨著支持度不斷變化的過程中, 在運(yùn)行時(shí)間上, 改進(jìn)后的算法明顯優(yōu)于Inter-Apriori算法.
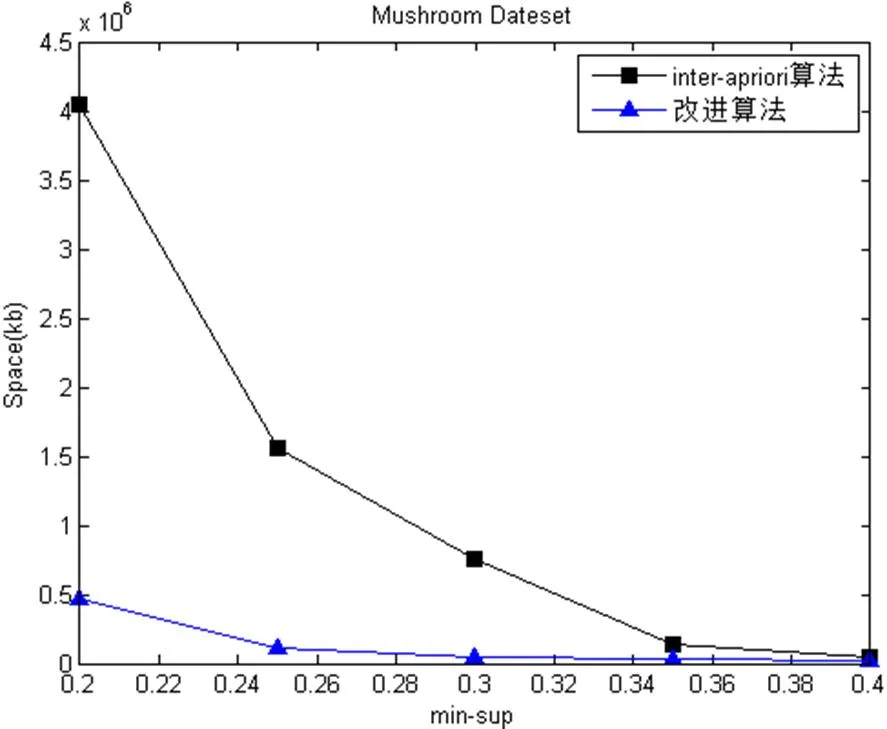
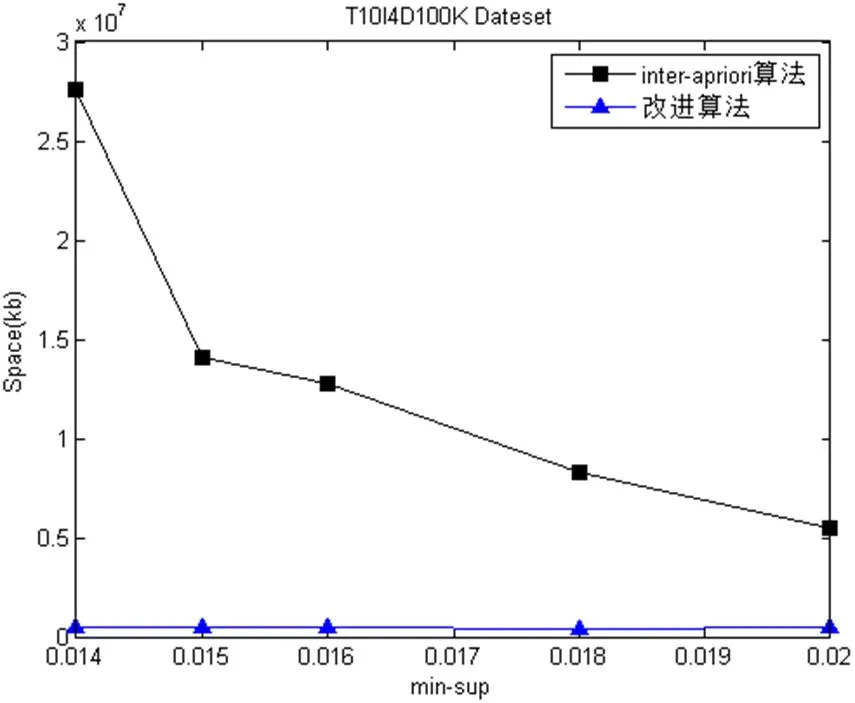
圖2 四種數(shù)據(jù)的運(yùn)行所占的內(nèi)存
從空間復(fù)雜度上看, 改進(jìn)后的算法明顯比Inter-Apriori算法少. 因?yàn)橹С侄仍酱髸r(shí), 產(chǎn)生的候選項(xiàng)集少, 進(jìn)而產(chǎn)生的頻繁項(xiàng)集越少, 算法運(yùn)行所占的空間存儲(chǔ)也越少. 在支持度較小的情況下, 對(duì)于密集型數(shù)據(jù)集Mushroom與Chess, 改進(jìn)后的算法運(yùn)行內(nèi)存變化接近平緩, 而Inter-Apriori算法的變化趨勢(shì)較大. 但是對(duì)于稀疏型數(shù)據(jù)集Nursery與T10I4D100K, 隨著支持度不斷變化的過程中, 在運(yùn)行內(nèi)存上, 改進(jìn)后的算法明顯優(yōu)于Inter-Apriori算法.
由圖1和圖2測(cè)試結(jié)果可知, 改進(jìn)算法的性能優(yōu)于Inter-Apriori算法. 無論是稀疏型還是密集型數(shù)據(jù)集,隨著minsup不斷減小的過程中, 改進(jìn)算法的性能和Inter-Apriori算法的性能差距逐步擴(kuò)大, 也體現(xiàn)了改進(jìn)后的算法良好的可伸縮性.
4 結(jié)論
本文建立了一種基于垂直型布爾矩陣的數(shù)據(jù)存儲(chǔ)結(jié)構(gòu)的挖掘算法, 利用定位和改變權(quán)值的大小, 來減少候選項(xiàng)目集的掃描時(shí)間和空間存儲(chǔ)的復(fù)雜度, 并且通過不同稠密度及規(guī)模的Mushroom、Chess、 Nursery、T10I4D100K數(shù)據(jù)集, 從時(shí)間和內(nèi)存上, 對(duì)兩種算法性能進(jìn)行了比較, 實(shí)驗(yàn)結(jié)果證明了改進(jìn)算法的性能比Inter-Apriori算法要高.
1 范明,范宏建.數(shù)據(jù)挖掘?qū)д?北京:人民郵電出版社,2011.
2 Agrawal R, Imielinaki T, Swami A. Mining association rules between sets of items in large databases. Proc. of ACM SIGMOD Conference on Management of Data. Washington, USA. ACM Press. 1993.
3 胡維華,馮偉.基于分解事務(wù)矩陣矩陣的關(guān)聯(lián)規(guī)則挖掘算法.計(jì)算機(jī)應(yīng)用,2014,3(S2):113–116.
4 苗苗苗,王玉英.基于矩陣壓縮的Apriori算法改進(jìn)的研究.計(jì)算機(jī)工程與應(yīng)用,2013,49(1):159–162.
5 羅丹,李陶深.一種基于壓縮矩陣的Apriori算法改進(jìn)的研究.計(jì)算機(jī)科學(xué),2013,40(12):75–79.
6 黃龍軍,段隆振,章志明.一種基于上三角項(xiàng)集矩陣的頻繁項(xiàng)集挖掘算法.計(jì)算機(jī)應(yīng)用研究,2006,11:25–26.
7 荀嬌,徐連成,楊仁華.基于排序索引矩陣的頻繁項(xiàng)集挖掘算法.計(jì)算機(jī)工程,2012,38(19):41–44.
8 張玉芳,熊忠陽.Eclat算法的分析及改進(jìn).計(jì)算機(jī)工程, 2010,36(23):28–30.
9 徐嘉莉,楊洪軍,趙茂娟,樊云.一種基于位運(yùn)算的頻繁閉項(xiàng)集挖掘算法.計(jì)算機(jī)應(yīng)用研究,2013,11(30):80–82.
10 張文東,尹金煥,等.基于向量的頻繁項(xiàng)集挖掘算法研究.山東大學(xué)學(xué)報(bào)(理學(xué)),2011,3(46):31–34.
11 劉步中.基于頻繁項(xiàng)集挖掘算法的改進(jìn)與研究.計(jì)算機(jī)應(yīng)用研究,2012,36(2):475–477.
12 紀(jì)懷猛.基于頻繁2項(xiàng)集支持矩陣的Apriori改進(jìn)算法.計(jì)算機(jī)工程,2013,39(11):183–186.
13 熊忠陽,陳培恩,張玉芳.基于散列布爾矩陣的關(guān)聯(lián)規(guī)則Eclat改進(jìn)算法.計(jì)算機(jī)應(yīng)用研究,2010,27(4):1323–1325.
14 Chen J, Xiao K. BISC: A bitmap itemset support counting approach for efficientfrequent itemset mining. ACM Trans. on Knowledge Discovery from Data, 2010, 4(3).
15 Goethals B. Frequent itemset mining dateset repository. http://fimi.ua.ac.be/date. [2004-12-02].
Improved Inter-Apriori Algorithm
CUI Shuang-Mi, ZHANG De-Sheng
(College of Science, Xi’an University of Technology, Xi’an 710054, China)
This paper establishes a mining algorithm based on the location and weight transaction item sets. It needs to scan the transaction database once. The algorithm adopts the vertical Boolean matrix to store transaction data, and the logic “and” operation and weight to calculate the support. Then it prunes through the searching location and combining the same columns of transaction matrix. Thereby the storage space and computing time used by the algorithm in the mining process can be reduced. The experimental results show that the improved algorithm performance has been significantly improved.
frequent itemsets; vertical type Boolean matrix; Inter-Apriori algorithm
國家自然科學(xué)基金(51379172)
2016-04-07;收到修改稿時(shí)間:2016-06-12
[10.15888/j.cnki.csa.005560]

