基于模糊PID算法的六自由度并聯機構控制研究

楊靖一，黃山云，丁祝順，荊龍賓

(北京航天控制儀器研究所，北京100039）

基于模糊PID算法的六自由度并聯機構控制研究

楊靖一，黃山云，丁祝順，荊龍賓

(北京航天控制儀器研究所，北京100039）

針對六自由度并聯機構難以實現高精度及快速響應的問題，分析六自由度并聯機構模型，提出基于模糊PID的六自由度并聯機構的控制算法。介紹了六自由度并聯機構的運動學反解模型及機械系統模型；在此基礎上確定模糊算法的模糊語言變量、隸屬函數和模糊規則，完成了六自由度并聯機構模糊PID控制器的設計。針對一組PID控制參數進行了仿真和實驗，結果表明，加入模糊算法的PID控制提高了系統的動態響應特性及運動精度。

運動學反解；模糊PID控制；六自由度；SimMechanics

Abstract：Due to the difficulties in the high precision and fast response of parallel mechanism，the parallel mecha?nism model is analyzed，the PID controller based on fuzzy algorithm is proposed to solve the motioned problem.Firstly，the inverse kinematics solution process of parallel mechanism is deduced.On the basis of analyzing the PID control and fuzzy control principle，the fuzzy language variables，membership function and fuzzy rules are determined，then six DOF parallel mechanism fuzzy PID controller is designed to improve the precision and response of the system.Finally，by the simulation and experiment analysis，the results show that the fuzzy PID controller improves the dynamic response performance and pre?cision.

Key words：inverse kinematics;PID fuzzy control;six?DOF;SimMechanics

0 引言

六自由度并聯機構基于Stewart平臺原理，由Stewart于1965年在 《A Platform with Six Degree》中首次提出，應用于飛行模擬器的運動研究。近年來，六自由度并聯機構以剛度大、結構穩定、承載能力強、精度高、動態性能好等優點成為機器人領域的一個研究熱點，已在并聯機器人、新型機床、大型射電望遠鏡、飛行模擬器、航空宇航對接器等領域獲得了廣泛應用。

六自由度并聯機構系統是一個多輸入、多輸出的復雜非線性系統，具有時變、強耦合和非線性等動力學特點，這給機構的控制研究帶來了很大的困難。在六自由度并聯機構的運動過程中，平臺的姿態變化反解出各桿的期望位移各不相同，甚至相差很大。而傳統控制方法一旦控制參數確定，在運動過程中就無法實時調整控制參數，所以傳統控制方法無法滿足系統在不同位姿情況下快速響應和高精度的要求。文獻[1]基于H∞魯棒控制，提出了一種并聯機構魯棒自適應控制，但其終究還是先進行線性化再進行設計的一種方法，無法完全適應六自由度并聯機構非線性控制的要求。文獻[2]提出了一種新型滑膜控制算法，其缺陷是控制器頻繁切換動作有可能造成跟蹤誤差在零點附近產生抖動的現象，而不能收斂到零。在此基礎上本文首先建立了六自由并聯機構模型，針對模型特性設計模糊PID控制器，并對其進行仿真及試驗研究，驗證了模糊PID在六自由度并聯機構控制上的優勢，達到了提高機構響應速度及精度的目的。

1 系統描述

六自由度并聯機構系統總體框圖如圖1所示，主要由運動學反解、控制系統和六自由并聯機構組成。運動學反解將輸入的期望位姿解算為六自由度并聯機構6根支腿的目標長度，同時根據反饋得到各支腿的實時長度，計算出各支腿的目標位移。將目標位移和目標位移的微分同時輸入控制系統，控制系統根據輸入量實時調整控制參數，輸出控制信號控制電機驅動，通過對6根電動推桿的控制使六自由度并聯機構輸出指定位姿。

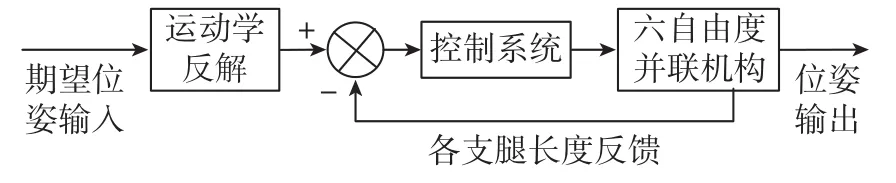
圖1 系統總體框圖Fig.1 Block diagram of system

下面將對系統運動學反解、控制系統的設計和六自由度并聯機構的建模進行詳細介紹。

2 系統建模

2.1 運動學反解

并聯機構運動學中有兩個基本問題，即機構的正解、反解問題。若己知機構主動件的位置，求解機構輸出件的位置和姿態，稱之為機構位置的正解；若已知輸出件的位置和姿態，求解機構輸入件的位置，稱之為機構位置的反解。由于正解的復雜性，以及無法獲得準確解，目前大部分并聯機構都采用反解的方法來求解運動學方程。

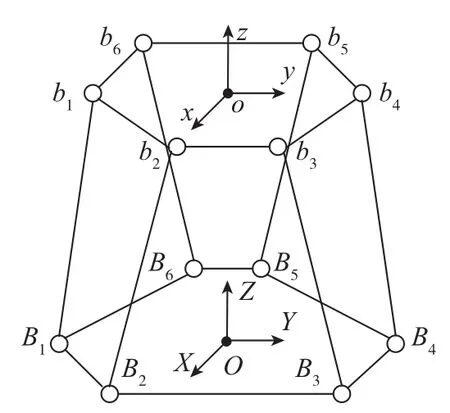
圖2 Stewart機構的運動學模型Fig.2 Dynamitic model of Stewart organization institution

圖2為Stewart機構的運動學簡化模型，固定坐標系O?XYZ建立在固定平臺上，動坐標系o?xyz建立在動平臺上，跟隨動平臺一起運動。建立固定坐標系和動坐標系兩者幾何矢量關系：

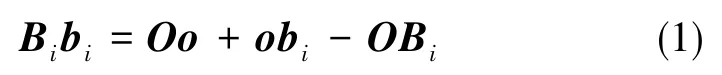
式中，Bi和bi是第i根支鏈的下固定鉸點和上運動鉸點。

并聯機構的運動逆解是從工作坐標反求鉸點坐標，并且有唯一解。位置逆解分析是利用坐標變換，將obi從動坐標系轉換到固定坐標系中，求Obi。動平臺在固定坐標系中有位置和姿態兩個參數，位置是動平臺的中心的位置(x，y，z）。姿態為動平臺的角姿態，設動平臺繞z軸旋轉的角為γ，繞y軸旋轉的角為β，繞x軸旋轉的角為α。

角位移γ、β、α對應的轉換矩陣R分別為［3］：

動平臺的姿態在空間上可以看到分別繞z軸、y軸、x軸旋轉得到，則：

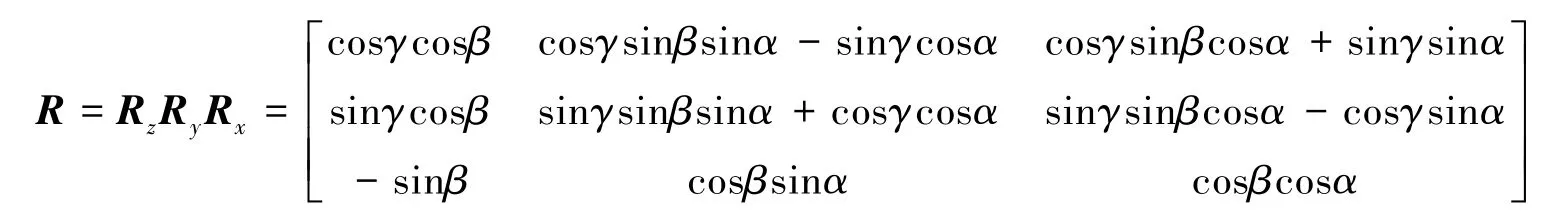
令Obi為Pi，obi為Pi′，Bibi為li，OBi為Bi，Oo為X，則［4?5］：

將式(2）代入式(1），得：

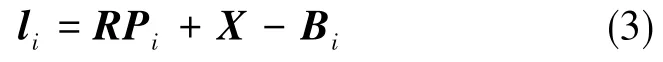
式中，li＝［lixliyliz］T。

則支鏈i對應的上下鉸點間的長度為：

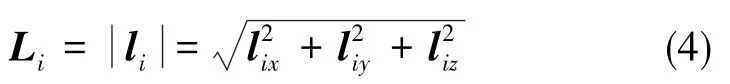
利用式(3）和式(4），即可通過輸出件的目標位姿，求解出機構的輸入量。

2.2 電動推桿建模

六自由度平臺系統的直流電動推桿不同于直流電機，它是通過輸入的電壓量U(t）轉換成距離量X(t），在此過程中電動推桿需要將U(t）逐步轉化為電流量I(t）、轉矩量T(t）、角速度量Ω(t）和最終的距離量X(t）。對于平臺位姿的控制實際需要從控制單個電動推桿開始，因此對于整個電動推桿的模型搭建和計算就顯得十分重要。圖3是本文所用的電動推桿經過拉普拉斯變換后的傳遞函數圖。

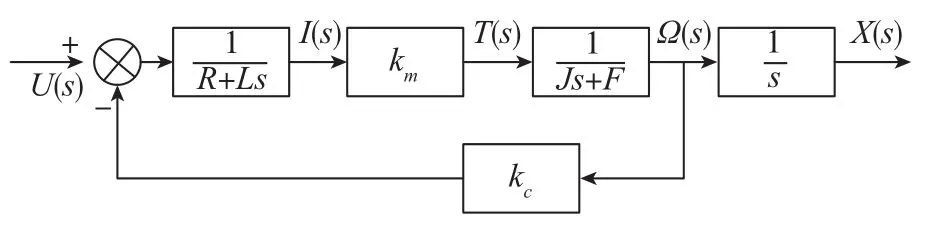
圖3 直流電動推桿傳遞函數圖Fig.3 Transfer function diagram of DC electric push rod

通過圖3可以得出輸入和輸出參數之間的關系：

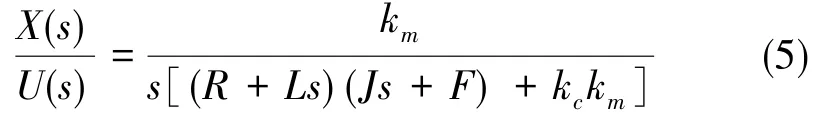
式(5）中，R和L分別代表直流電機的電樞電阻和電感，km是電子轉矩和電樞電流之間的系數，J和F是拖動系統整體轉動慣量和摩擦轉矩，kc是電動推桿的反電動勢系數。

2.3 并聯機構的SimMechanics建模

目前，對六自由度并聯機構的仿真大部分使用的是ADAMS，或者是ADAMS同Matlab的聯合仿真，因涉及不同軟件的接口問題，數據交換比較復雜。本文利用Simulink中的SimMechanics來構建物理模型，SimMechanics模塊庫中包含了組成一個完整機械系統所需要的基本模塊，利用這些模塊可以方便、準確地搭建出機械系統模型［6?7］。

六自由度機構結構主要由上、下平臺和6根桿組成。其中，上平臺由實體庫下Body創建，通過參數設置對話框，設置上平臺的幾何屬性、質量屬性和初始狀態。幾何屬性包括上平臺質心坐標以及同伸縮桿連接點的坐標。固定下平臺直接選用Ground模塊建模，設定系統環境，包括質量、機械系統維數及分析模式等。定義每根桿的驅動力Fi(i＝1，…，6）為機械系統輸入，桿的位移Pi(i＝1，…，6）作為機械系統輸出。

六自由度機構伸縮桿由上伸縮桿和下伸縮桿組成，使用實體庫、約束庫和約束激勵庫建立模型。在模型中添加伸縮桿同上下平臺的接口、上伸縮桿和下伸縮桿、上伸縮桿和上平臺的萬向副約束、上伸縮桿和下伸縮桿間的圓柱副，同時添加力驅動圓柱副、移動傳感器測量伸縮桿的位移、下伸縮桿和下平臺間添加萬向副約束。最終，建立的模型如圖4所示。

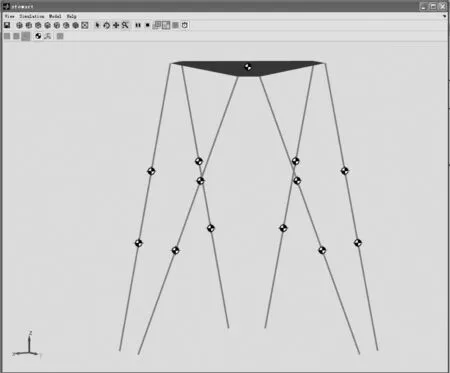
圖4 并聯機構的SimMechanics模型Fig.4 SimMechanics model of parallel mechanism

3 模糊PID控制器設計

通過以上對模型的分析，可以看出在機構運動過程中不同位姿反解得到的驅動桿的位移各不相同，如果在運動過程中使用同一組不變的控制參數，會對系統的響應速度及精度造成影響。本文提出在PID的基礎上，引入模糊控制來改善PID控制在運動過程中不能實時調整參數對六自由度并聯機構響應速度及精度帶來的影響。

3.1 模糊PID控制算法

六自由度并聯機構模糊PID控制器為基于誤差驅動的增益調整型控制，由PID控制器和模糊控制器兩部分組成。整個模糊PID控制器的結構框圖如圖5所示。

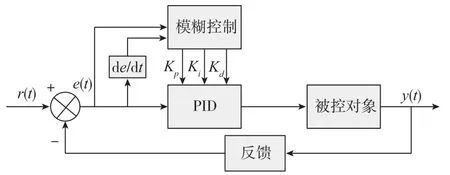
圖5 模糊PID控制原理圖Fig.5 Schematic diagram of fuzzy PID control

常規PID控制器的算法：

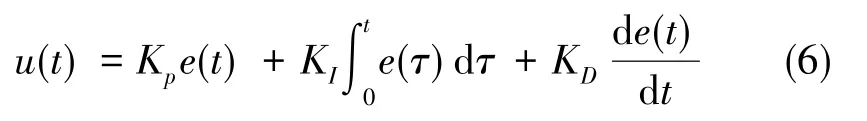
式中，KP為比例控制系數，KI為積分控制系數，KD為微分控制系數，e(t）為期望輸入r(t）與實際輸出y(t）之間的差值。

模糊控制器主要由4部分組成：模糊化、知識庫、模糊推理和清晰化［8?10］。

輸入輸出變量的確定：由于模糊PID控制器主要針對PID的3個參考進行調整，能夠實現參數自調整的效果。同時對于該控制器的輸入，選用偏差e和偏差變化率 de/dt作為輸入，輸出為PID 控制的 3 個參數：Δkp、Δki、Δkd。參數kp、ki、kd可由以下公式計算得出：

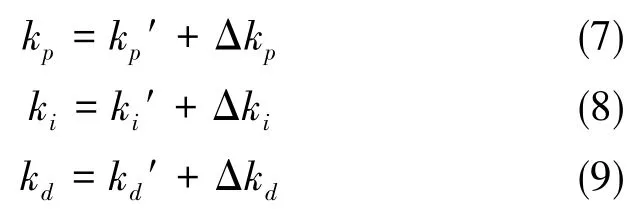
式中，kp′、ki′、kd′均為初始值，即為系統所要改進的傳統PID的控制系數。

將輸入輸出變量所對應的模糊子集以及模糊論域定義為：｛E｝＝｛EC｝＝｛－0.3，－0.2，－0.1，0，0.1，0.2，0.3｝；｛Δkp｝＝｛－30000，－20000，－10000，0，10000，20000，30000｝；｛Δki｝＝｛－300，－200，－100，0，100，200，300｝；｛Δkd｝＝｛－750，－500，－250，0，250，500，750｝。

其中，｛E｝、｛EC｝、｛Δkp｝、｛Δki｝和｛Δkd｝的模糊子集都定義為：｛NB(負大），NM(負中），NS(負小），ZO(零），PS(正小），PM(正中），PB(正大）｝。

模糊規則的確定：根據上文對PID3個參數控制作用的分析，結合專家庫中PID控制規則，得出關于Δkp、Δki、Δkd3個參數的控制規則表。如表1所示，文中只給出了Δkp的控制規則，Δki和Δkd的控制規則類似。

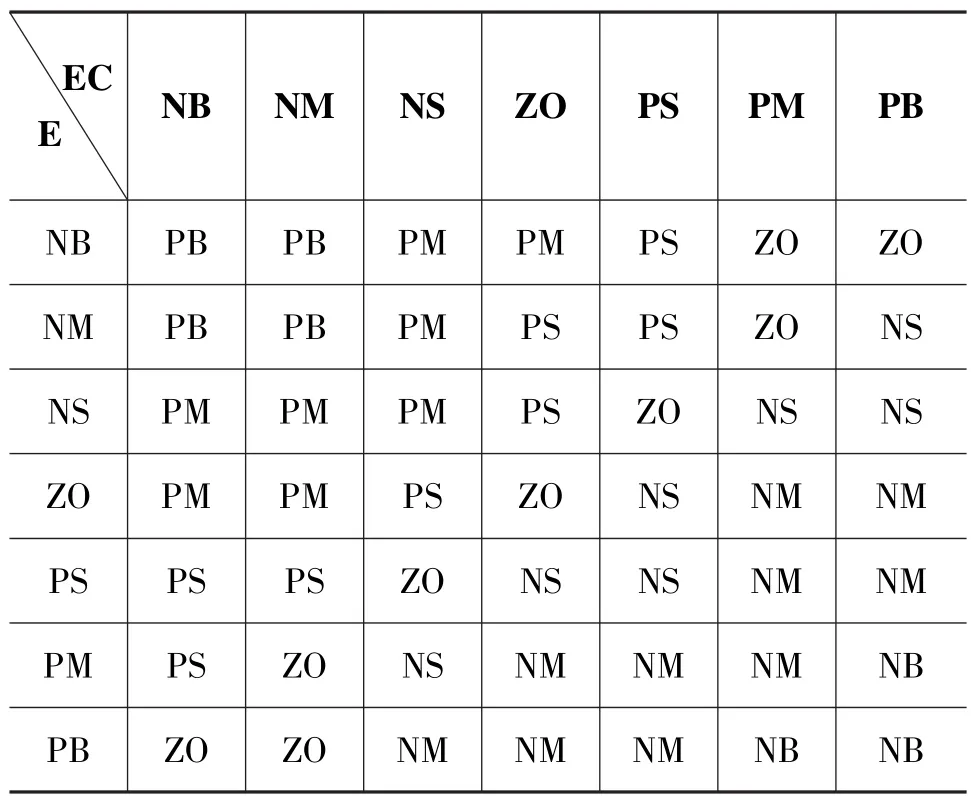
表1 ΔKp模糊規則表Table 1 Rule sheet ofΔKpfuzzy

3.2 模糊PID控制器設計

模糊PID是在普通PID基礎上，根據經驗對控制參數的實時修正，需要先搭建一個PID控制模型，如圖6所示。系統輸入兩個6×1矩陣，pos和r＿pos分別代表傳感器觀測的6根桿實時位移和經過運動學反解得出的6根桿的目標位移，計算偏差量輸入到PID控制器得到一個6×1矩陣Force，即施加在6根桿上的力。其中，kp＝80000、ki＝500、kd＝1800。

由于在并聯機構的運動過程中給定目標姿態，經運動學反解得出的各桿目標位移各不相同，所以本文針對6根桿分別設計控制器。6個模糊PID控制器可以根據桿的目標位移與實際位移的偏差量及偏差量變化率實時更新控制參數，達到更好的控制效果。下面以其中1根桿為例設計模糊PID控制器。

在PID控制器基礎上引入模糊控制，如圖7所示。選擇與傳統PID的控制參數作為模糊PID控制的初始控制參數，添加Fuzzy Logic Controller模塊，分別設置輸入輸出的論域及模糊規則，選擇Max?Min的推理算法和面積中心法的清晰化方法。其中，模糊控制器的輸入量為目標桿位移和實際桿位移的偏差量，即桿的伸縮量；以及伸縮量的變化率，輸出為Δkp、Δki、Δkd，分別和初始控參數kp、ki、kd作和，得到新的控制參數。

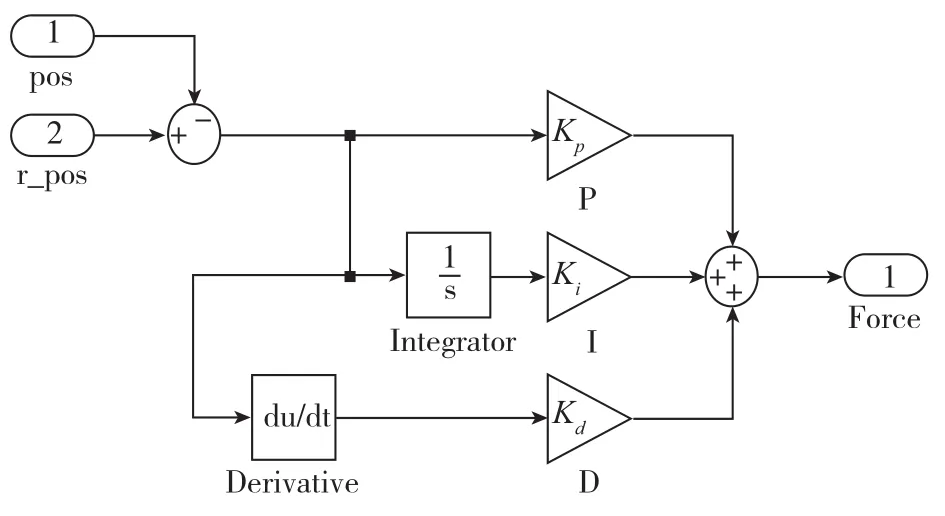
圖6 PID控制框圖Fig.6 The PID control frame

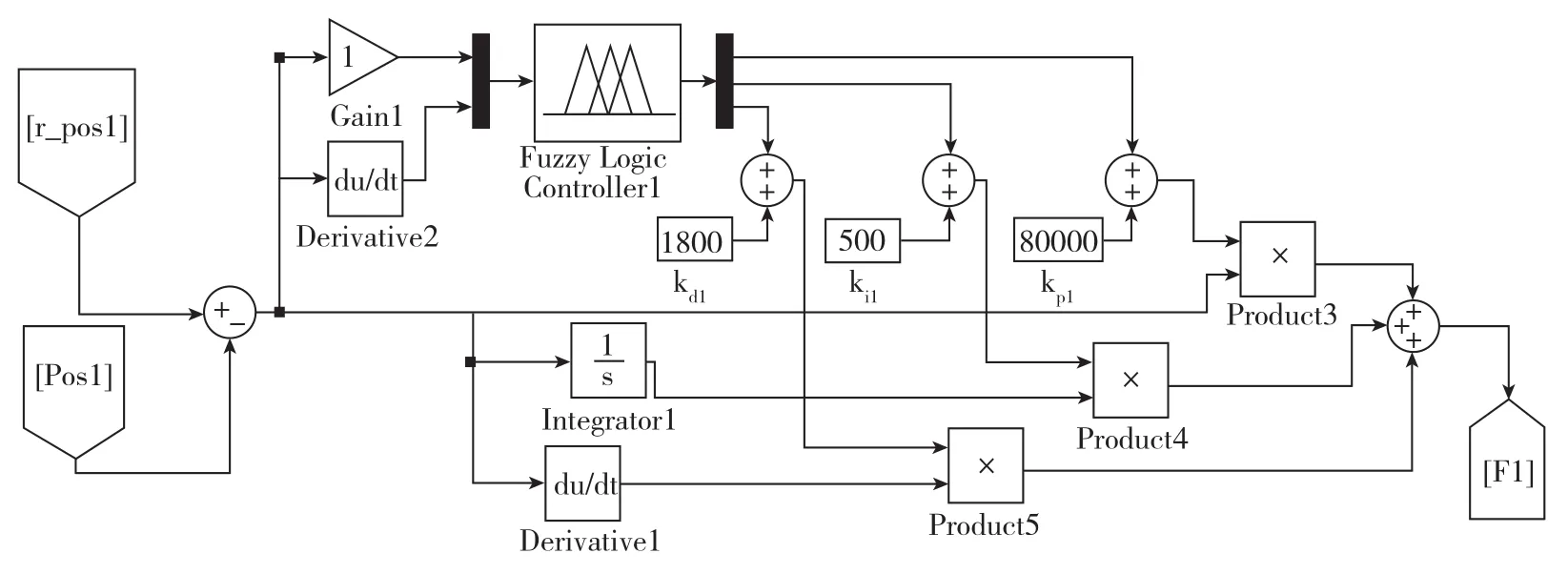
圖7 模糊PID控制框圖Fig.7 Control frame of fuzzy PID

4 控制系統仿真分析

采用 Matlab/Simulink軟件對系統進行仿真，仿真平臺的搭建與各模塊的連接如圖8所示。Leg Trajectory為運動學反解模塊，Controller為控制器模塊，Plant為機構的機械系統模塊。

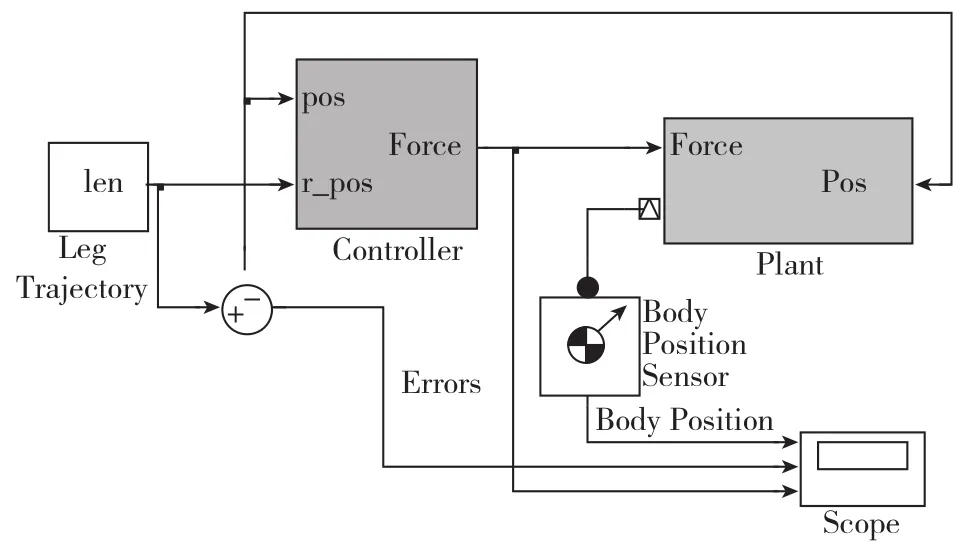
圖8 仿真總體框圖Fig.8 Overall model of simulation

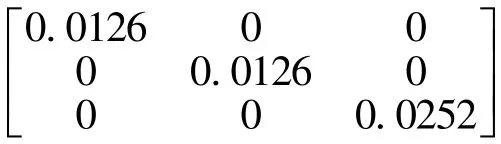
在3個進動方向和3個轉動方向分別輸入幅值為0.1m和1°、頻率為1Hz的正弦信號，針對同一組控制參數分別對傳統PID和模糊PID進行仿真，得到曲線如圖9所示。

根據仿真結果分析，得到的傳統PID仿真及模糊PID的仿真的幅值、誤差平均值及誤差方差如表2所示。從圖9和表2中可以看到，加入模糊算法的PID控制相對傳統PID控制在響應速度及精度上都有所改善。

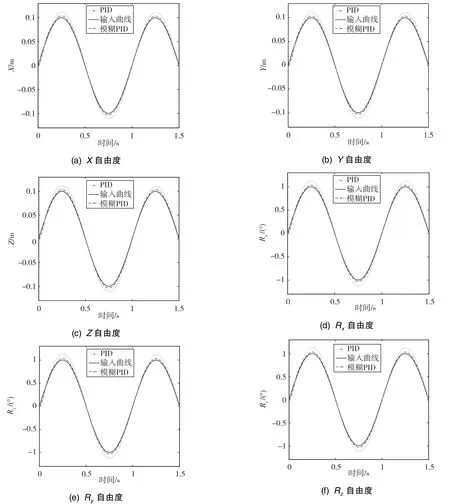
圖9 正弦輸入輸出對比Fig.9 The comparison of sine response

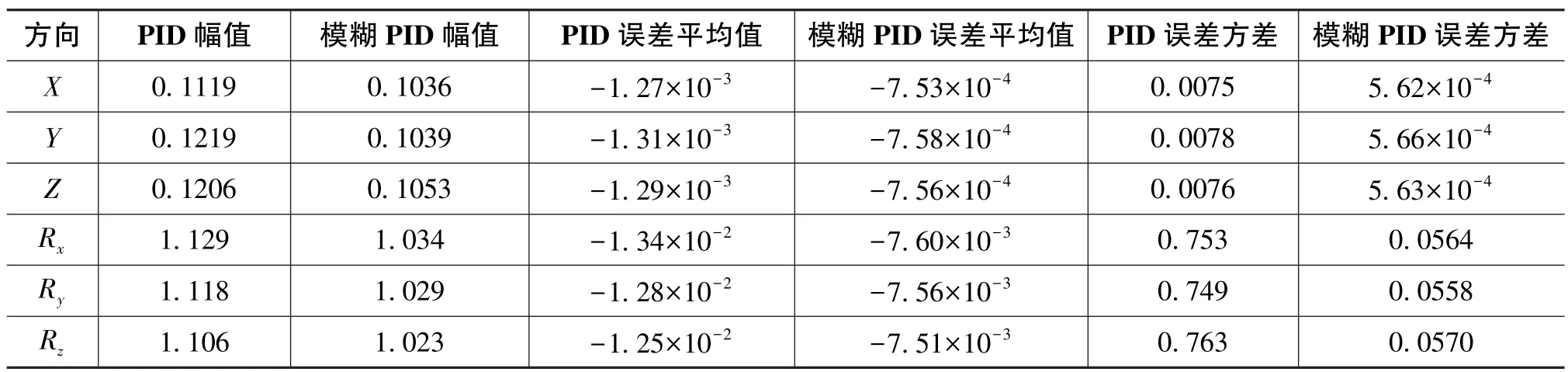
表2 設定信號為1Hz的仿真及實驗結果Table 2 Results of simulation and experiment about input signals with frequency of 1Hz

5 實驗結果分析

利用實驗室現有六自由度并聯機構，將模糊PID算法移植到控制板上。由于在各自由度的運動中得到的實驗結果類似，這里以繞Y方向的轉動為例，輸入控制指令使并聯機構繞Y軸跟蹤幅值為1°、頻率為1Hz的正弦曲線轉動。利用姿態板采集上平臺轉動的角度信息，傳統PID與模糊PID控制的輸出曲線如圖10所示。可以看出，模糊PID控制的響應速度及精度優于傳統PID控制的響應速度及精度。

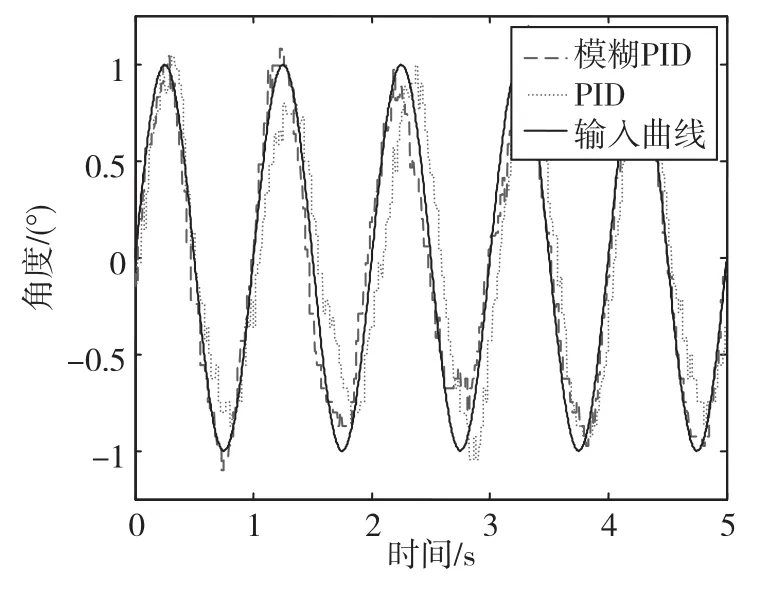
圖10 正弦輸入輸出對比Fig.10 The comparison of sine response

傳統PID與模糊PID控制的輸出曲線與輸入曲線作差取絕對值得出誤差曲線，如圖11所示。模糊PID控制誤差均值為0.0597，方差為0.0021。傳統PID控制誤差均值為0.1348，方差為0.0056。從分析結果可知，在不同位姿情況下模糊PID控制的控制效果相對于傳統PID控制的控制效果有所改善。

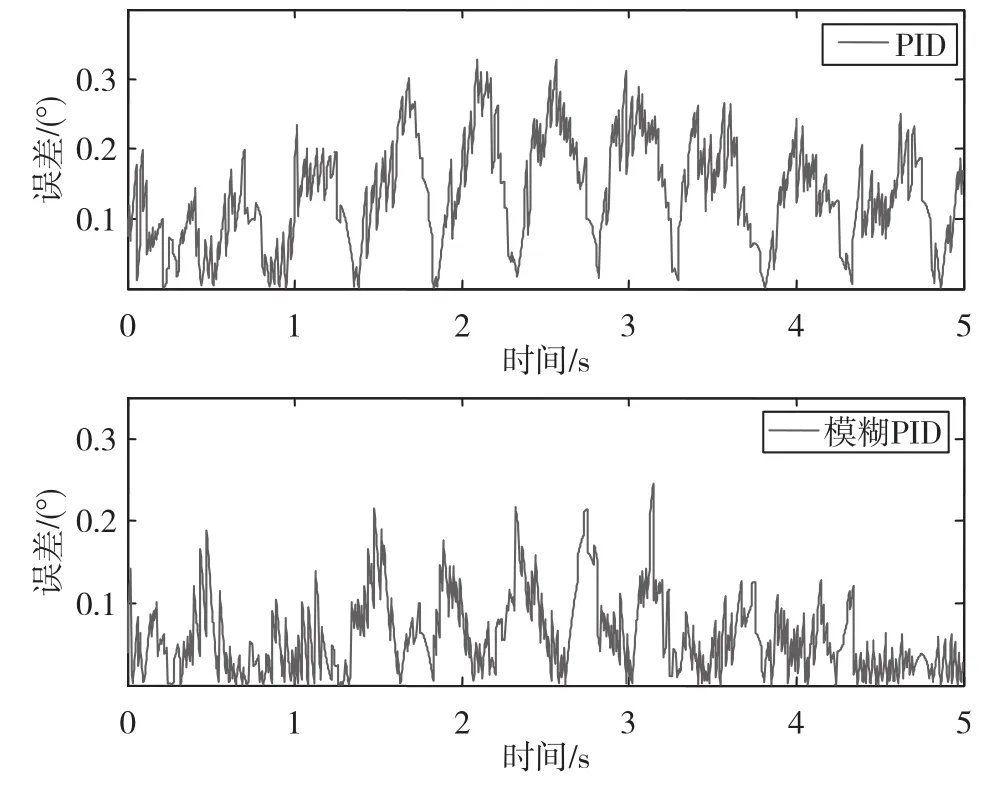
圖11 正弦跟蹤誤差對比Fig.11 The comparison of sine response error

6 結論

針對六自由度并聯機構難以實現高精度及快速響應的問題，本文針對六自由度并聯機構特性在傳統PID的基礎上引入模糊算法，使系統在控制過程中可以實時調整控制參數，建立了并聯機構的仿真模型，然后對所建立的并聯機構模型進行研究及仿真分析，并在實際的六自由度并聯機構中進行驗證。結果表明，加入模糊控制的PID改進了傳統PID控制在六自由度并聯機構中響應速度和精度的不足。

[1]吳東蘇.輕型飛行模擬器運動平臺先進控制技術研究[D].南京航空航天大學,2007.WU Dong?su.Advanced control technology research of light flight simulator motion platform[D].Nanjing University of Aeronautics and Astronautics,2007.

[2]Zhao D Y,Li S Y,Zhu Q M.A new TSMC prototype robust nonlinear task space control of a 6?DOF parallel ro?botic manipulator[J].International Journal of Control,Au?tomation,and Systems,2010,8(6）:1189?1197.

[3]陸元九.慣性器件（上冊）[M].北京:中國宇航出版社,1993.LU Yuan?jiu.Initial devices(1st）[M].Beijing:China Aer?ospace Press,1993.

[4]朱曉龍,頓向明.一種五自由度機械臂逆運動學求解的幾何法[J].機械與電子,2014,28(5）:77?80.ZHU Xiao?long,DUN Xiang?ming.A geometrical method for inverse kinematics of 5?DOF manipulator[J].Machinery＆ Electronics,2014,28(5）:77?80.

[5]黃真,孔令富,方躍法.并聯機器人機構學理論及控制[M].北京:機械工業出版社,1997.HUANG Zhen,KONG Ling?fu,FANG Yue?fa.Theory of mechanism and control of parallel robot[M].Beijing:China Machine Press,1997.

[6]李沛,楊小強,李煥良,等.基于Matlab/SimMechanics的六自由度并聯運動平臺建模與分析[J].機械與電子,2016,34(3）:75?80.LI Pei,YANG Xiao?qiang,LI Huan?liang,et al.Modeling and analysis of six?DOF parallel platform based on Matlab/SimMechanics[J].Machinery ＆ Electronics,2016,34(3）:75?80.

[7]張壽鳳,袁中凡,李彬彬,等.基于積分分離PID控制的Stewart六自由度臺仿真[J].機械科學與技術,2009,28(2）:214?217.ZHANG Shou?feng,YUAN Zhong?fan,LI Bin?bin,et al.Simulink of a six?DOF Stewart platform integral?separated PID control[J].Mechanical Science and Tech?nology for Aerospace Engineering,2009,28(2）:214?217.

[8]Feng G.An approach to adaptive control of fuzzy dynamic systems[J].IEEE Transactions on Fuzzy Systems,2002,10(2）:268?275.

[9]Park K H,Hwang D H,Bien Z.A study on the robustness of a PID?type iterative learning controller against initial state error[J].International Journal of Systems Science,1999,30(1）:49?59.

[10]陳政文.基于模糊PID控制的退火爐溫度控制系統的研究[D].武漢工程大學,2014.CHEN Zheng?wen.Annealing furnace temperature control system based on fuzzy PID control[D].Wuhan Institute of Technology,2014.

Research on the Controller of a 6?DOF Parallel Platform Based on the Fuzzy PID Strategy

YANG Jing?yi,HUANG Shan?yun,DING Zhu?shun,JING Long?bin
(Beijing Institute of Aerospace Control Devices,Beijing 100039）

U666.1

A

1674?5558(2017）01?01362

10.3969/j.issn.1674?5558.2017.05.006

2017?01?06

楊靖一，男，碩士，導航、制導與控制專業，研究方向為控制。