連鑄中間包熱損失影響因素的數值分析

杜亞偉 杜海明 杜玉蘭 單 強 蘇 彬

(安陽鋼鐵集團有限責任公司)

連鑄中間包熱損失影響因素的數值分析

杜亞偉 杜海明 杜玉蘭 單 強 蘇 彬

(安陽鋼鐵集團有限責任公司)

為掌握典型工況條件對連鑄過程中中間包熱損失的影響程度，基于大型數模分析軟件ANSYS 熱分析模塊，對普碳低合金鋼種連鑄中間包熱損失影響因素進行了數值分析。結果表明：1)當鋼水較大面積暴露在環境中時，環境溫度的變化將顯著影響中間包鋼水溫度的變化；2)實際生產中應盡量減少中間包操作孔敞開的時間；3)中間包保溫層采用新型隔熱保溫材料將大幅改善其保溫效果；4)覆蓋劑的合理選用及正確使用有助于降低上鋼溫度。

連鑄中間包 熱損失 數值模擬

AbstractIn order to grasp the influence of the typical operating conditions on the heat loss in the continuous casting tundish，the numerical analysis on the influence factors of the heat loss in the tundish in continuous casting for the carbon-steel and low alloy steel，based on the thermal analysis module of the software ANSYS，had been carried out. The results showed that，1)The steel temperature could be affected significantly when the molten steel ws exposed to the environment in large area；2)In practice，the opening time of the operation hole on the tundish should be minimized；3) The heat preservation effect in the tundish wounld be improved，if the new heat insulation materials were applied to the insulation on the tundish；4)Reasonable selection and proper use of the covering agent could help reduce the end point temperature of the LF refining.

KEYWORDScontinuous casting tundish heatloss numerical simulation

0 前言

溫度是整個煉鋼生產的生命線，中間包鋼水溫度作為連鑄流程乃至整個煉鋼流程溫度控制的一個重要環節，其溫度高低、波動直接或間接影響鋼材質量和產量。

對中間包溫度的研究，20世紀80年代以來，國內雖相繼開發并應用了各種中間包測溫技術和設備，如寶鋼等企業利用連續測溫裝置對中間包進行了熱測試[1]。并且以往對中間包熱狀態的研究多將其作為鋼包熱循環過程的一個組成部分，對影響中間包溫度變化規律的影響因素研究并不多見。因此，要了解中間包溫度的變化規律和穩定控制中間包溫度，必須對影響中間包溫度的因素進行分析和研究，才能更好的實現中間包的溫控。

以某鋼廠3#鑄機的中間包澆鑄過程為例，擬采用大型商用有限元分析軟件ANSYS11.0建立中間包的相關熱損失數學模型，著重就中間包所處的環境溫度變化、中間包操作孔封閉與否、中間包保溫層厚度及材質改變等幾種工況條件進行相關數值分析，以期找到影響中間包溫度變化的規律。同時，就中間包澆注過程的溫降規律進行模擬分析，為中間包內鋼液溫降控制提供理論依據，從而指導生產實踐。

1 中間包溫度模型的建立

以某鋼廠3#鑄機用中間包(正常工作噸位～53 t，液面高度～1 200 mm)為研究對象，以普碳低合金鋼為例，建立中間包溫度模型進行數值模擬。中間包結構尺寸及各部分耐材尺寸和相應的物性參數分別見表1、表2、表3[2]和表4[3]。

表1 中間包包體外形尺寸 / m

表2 中間包包底及側壁各層厚度 / m

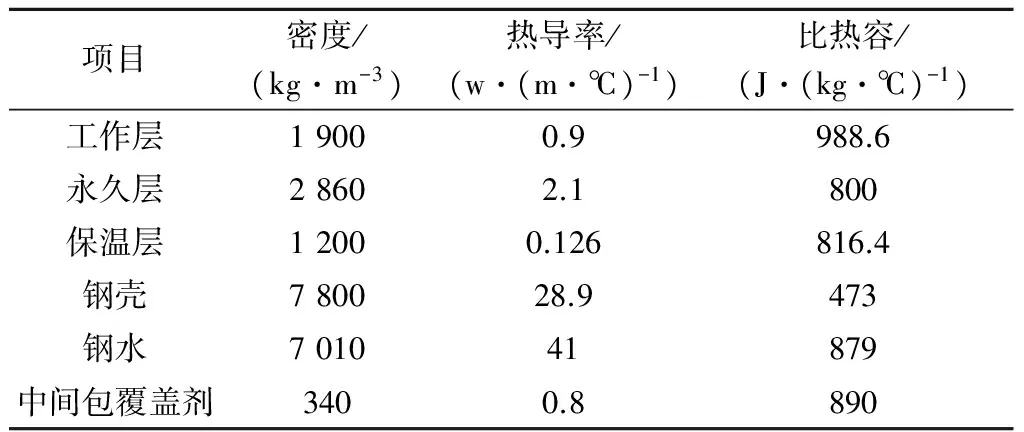
表3 中間包各組成部分的熱物性參數

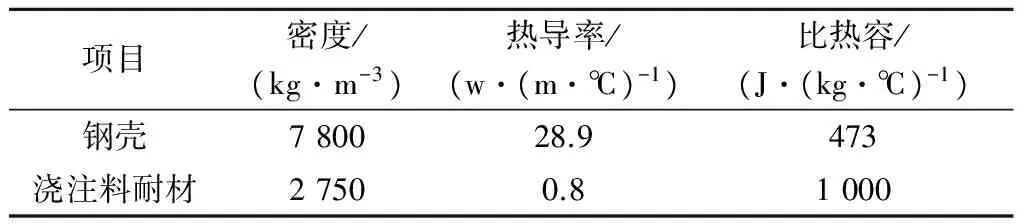
表4 中間包包蓋尺寸及熱物性參數

注：1. 包蓋各操作孔總面積約占包蓋平面面積的30%～40%； 2. 鋼殼厚度約8 mm，鋼纖維澆注料厚度約200 mm。

1.1 ANSYS模擬過程簡述

ANSYS求解模型分3個步驟[4]：前處理、求解、后處理。中間包ANSYS數值模擬的具體程序為：“進入前處理器”→“定義單元類型及材料熱物性參數”→“建立中間包實體模型”→“網格劃分”→“定義表面效應單元及空間節點”→“進入求解器”→“施加穩態邊界條件”→“進行穩態求解”→“刪除穩態邊界條件，將穩態結果作為瞬態分析初始條件并重新施加邊界條件”→“進行瞬態求解”→“進入后處理器”→“繪制溫度分布圖、時間-溫度曲線圖，輸出結果”→“結果保存”。

1.2 中間包實體模型的建立

在ANSYS前處理模塊中對中間包建立實體模型。利用查閱的相關物性參數在ANSYS前處理中分別定義單元類型(SOLID70、SURF152)、材料密度、熱導率、比熱容、輻射率。建立1/4中間包有蓋有覆蓋劑的實體模型。建立好中間包物理模型后對其進行網格劃分，施加邊界條件并求解。

這里需要說明的是，網格劃分主要分為映射網格劃分(mapped)和自由網格劃分(free)，事實上，完全靠軟件的自由網格劃分可能容易產生尖銳或邊長比很大的不良單元，但經過控制的自由網格劃分的精度與映射網格劃分差別不大[5]。采用自由網格劃分所產生的三角形單元或四面體單元將使自由度大大增加，從而造成運算量的增加，隨著機器配置的逐漸增強，運算量大的問題已經得到很好的解決，由于中間包各面結構復雜，故本文采用自由網格劃分方法與映射劃分相結合的方法，因覆蓋劑層比較薄，所以覆蓋劑的網格劃分尺寸較小，為0.05 m，而其他位置網格尺寸分別為0.1 m和0.5 m，劃分網格后有蓋有覆蓋劑中間包如圖1、圖2所示。

圖1 有蓋有覆蓋劑1/4中間包網格劃分圖2 包蓋4操作孔封閉1/4中間包網格劃分

在上述1/4中間包有限元模型基礎上對模型施加初始條件及邊界條件：1)進入Aux12，求解出中間包內輻射矩陣；2)再進入前處理器，選擇單元MATRIX50(超單元)，并設置單元KeyOption為熱輻射分析；3)讀入輻射矩陣，刪除生成輻射矩陣的SHELL57單元；4)先定義分析類型為穩態分析；5)定義中間包內表面初始溫度，外表面溫度；6)進行求解；7)設置分析類型為瞬態分析；8)刪除穩態時施加的邊界條件；9)定義中間包外表面、內壁及覆蓋劑上表面對流換熱系數；10)定義外界空氣溫度，覆蓋劑上表面空氣溫度；11)定義鋼水初始溫度；12)設置輸出控制為全部結果；13)定義求解傳熱時間；14)定義時間步長；15)求解。

2 影響中間包溫度變化的因素分析

前面簡述了利用有限元分析軟件對中間包溫度模型的建模過程，本部分將在模擬的基礎上求解中間包溫度模型，并較為系統的分析影響中間包鋼水溫度的各影響因素。

2.1 冬夏季不同環境溫度對中間包鋼水溫度的影響

中間包有蓋有覆蓋劑，分操作孔封閉與不封閉兩種模擬條件，模擬不同環境溫度對中間包鋼水溫度變化的影響程度，中間包鋼水的“溫度-時間”曲線圖分別如圖3、圖4所示。環境溫度取值：冬季設定為0 ℃，夏季設定為40 ℃。

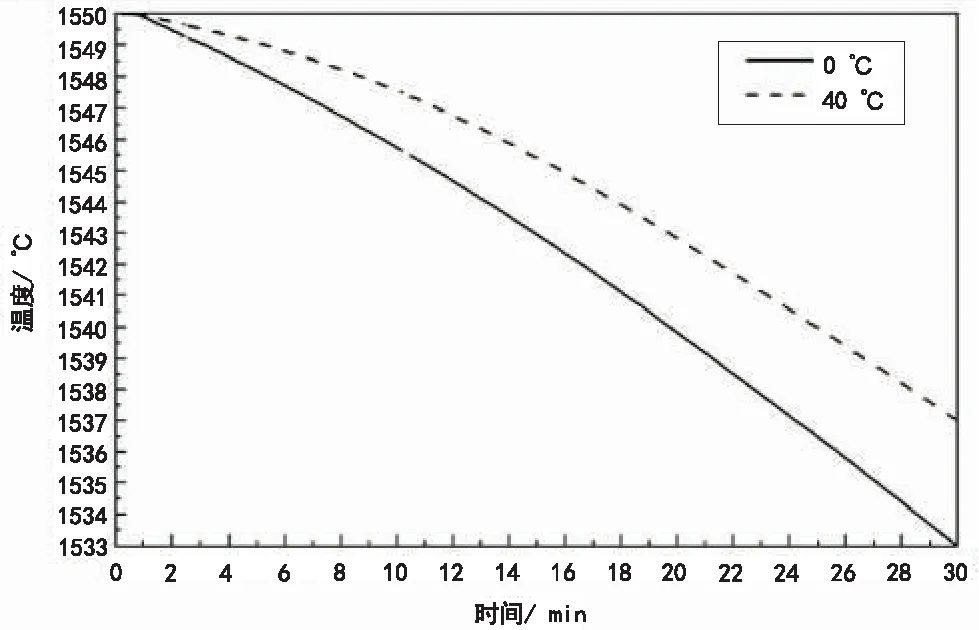
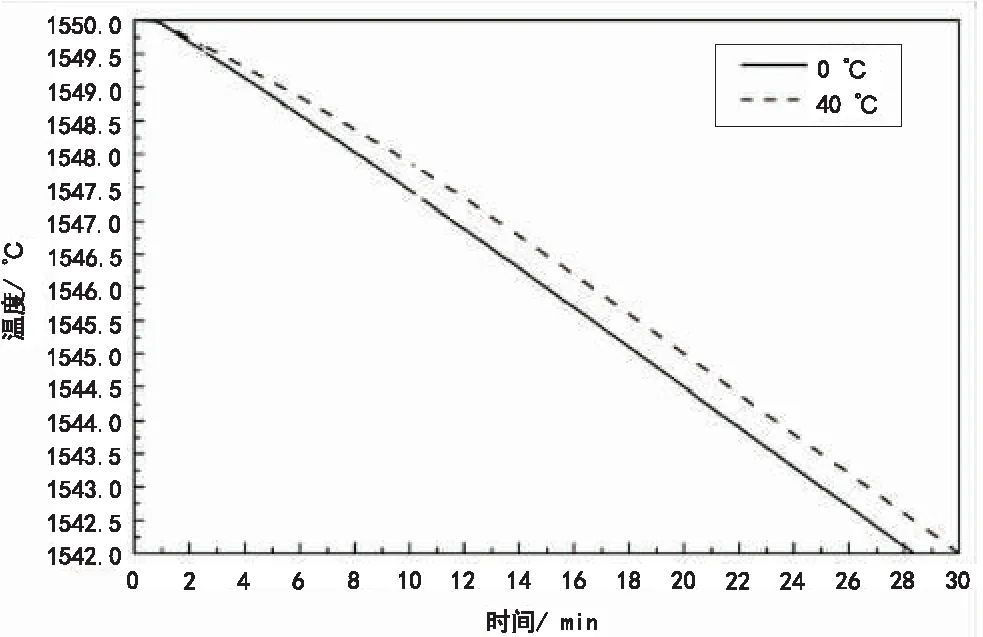
圖3 環境溫度對鋼水溫度的影響(不封閉)圖4 環境溫度對鋼水溫度的影響(封閉)

1)不封閉情況：從圖3可以看出，30 min內中間包鋼水溫度在外界環境不同時存在一定的差異。其他條件相同時，30 min內，外界環境為0 ℃時要比外界環境為40 ℃時多下降3 ℃左右。從這種情況分析，外界環境溫度是影響中間包溫度穩定的一個相對因素。

2)封閉情況：從圖4可以看出，30 min內，外界環境溫度從0 ℃升高到40 ℃，中間包內鋼水溫度的相對變化已經很小，相差僅0.5 ℃左右。

上述兩種情況的分析顯示，當鋼水較大面積暴露在環境中時，外界環境溫度的變化將顯著影響中間包鋼水溫度的變化。

2.2 包蓋各操作孔封閉與否對中間包鋼水溫度的影響

為掌握包蓋各操作孔封閉與不封閉情況下，對中間包鋼水溫度的影響程度，重點模擬了中間包有蓋有覆蓋劑，相同環境溫度(夏季為40 ℃)、相同保溫層厚度(5 mm)及相同邊界與初始條件下中間包鋼水溫度隨時間的變化，結果如圖5所示。

從圖5可以看出：1)各操作孔封閉情況中間包鋼水溫降要小于操作孔敞開情況的溫降；2)30 min內“封閉情況”要比“敞開情況”少下降3.6 ℃，“敞開情況”對中間包溫度的影響超過了“0 ℃外界環境溫度對中間包溫降”的影響程度。

由此可見，中間包操作孔封閉與否對中間包保溫有重要的影響，實際生產中應盡量減少中間包操作孔敞開的時間。

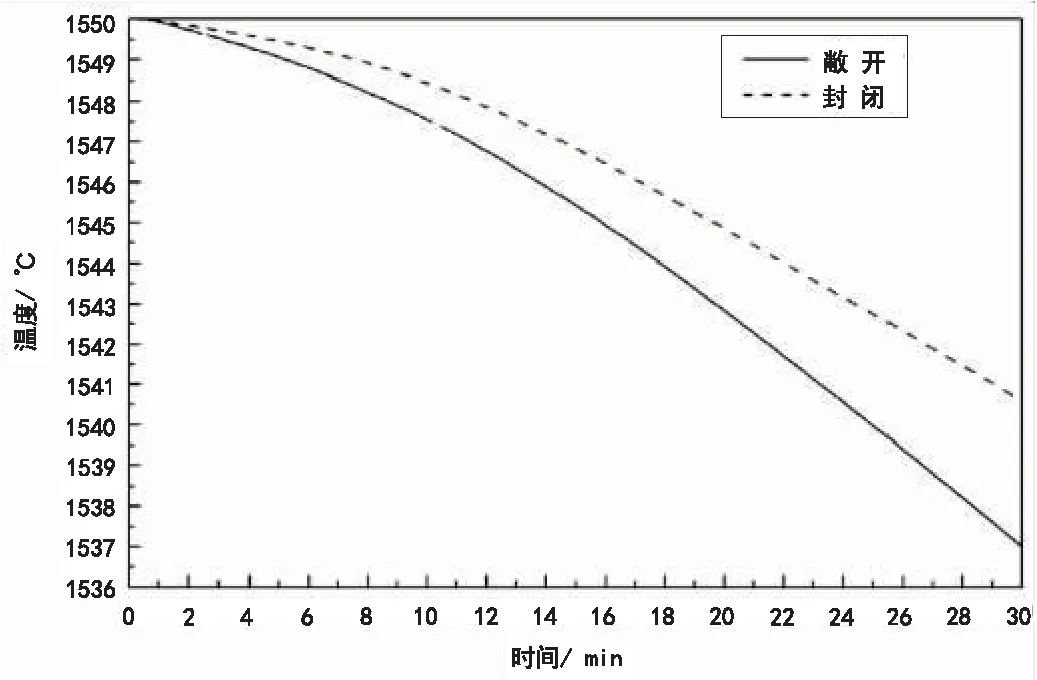
圖5 操作孔封閉與否對鋼水溫度的影響

2.3 不同保溫層厚度對中間包鋼水溫度的影響

中間包包壁分為4層，從外到內分別為鋼殼、保溫層、永久層和工作層。因中間包工作條件的需要，工作層和永久層的厚度幾乎不變，而鋼殼對中間包的保溫作用又沒有太大影響。所以，要有效提高中間包的保溫性能，只能通過改變中間包保溫層的厚度來實現。該部分通過討論“不同保溫層厚度”對中間包鋼液溫降的影響。

模擬計算條件為：中間包有蓋有覆蓋劑，包蓋各操作孔封閉情況下，相同環境溫度(夏季為40 ℃)、不同保溫層厚度(0.005 m、0.010 m、0.015 m、0.020 m(設計厚度)、0.030 m、0.035 m、0.040 m和0.050 m)及相同邊界與初始條件下建立中間包30 min鋼水溫度隨時間變化的溫度模型，如圖6所示；相應取30 min時0.70 m處中間包寬面側壁保溫層中部(8種不同厚度方案)的“溫度-厚度”曲線，如圖7所示。

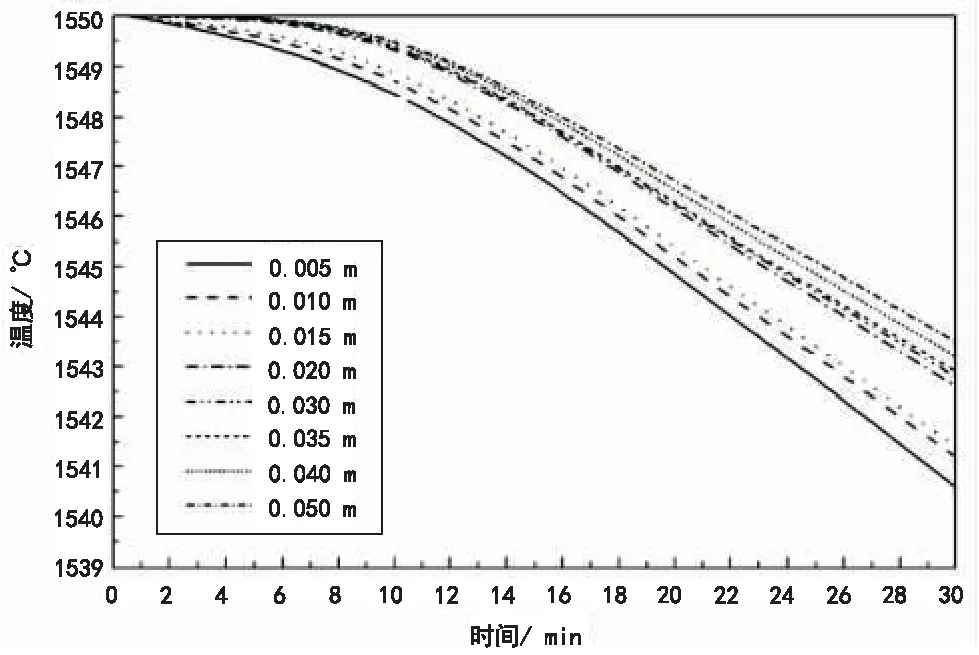
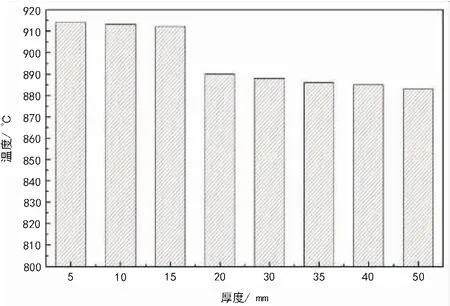
圖6 保溫層厚度對鋼水溫度的影響圖7 保溫層8種厚度方案溫度分布圖

由圖6、圖7可以看出：

1)鋼水溫度在保溫層厚度處于15 mm和20 mm時出現明顯轉折；保溫層厚度提高到20 mm后，鋼水“溫度-時間”曲線明顯趨緩并有所提高，30 min后鋼水溫度也相應提高了3 ℃左右。

2)保溫層8種厚度溫度分布圖同樣表明，在保溫層厚度提高到20 mm后，保溫層中部溫度明顯下降約20 ℃，這足以使中間包包體鋼殼溫度下降20 ℃以上。之后提高保溫層厚度的4種方案，溫度降低程度較小，則說明繼續提高保溫層厚度意義并不大。

由此可見，適當增加保溫層厚度對中間包的保溫效果有一定的影響。而當保溫層厚度增加到40 mm時與20 mm溫度變化基本相同。可知雖然增加中間包保溫層厚度可減少中間包向包外的散熱量，但其厚度增加到一定程度后繼續增加保溫層厚度對中間包保溫效果影響己經不大。

3)如果中間包保溫層在其材質不變的條件下，將保溫層實際投用厚度(目前實際投用厚度為～15 mm)保證在20 mm的設計厚度(永久層澆注料壓實后的實際厚度)以上，中間包保溫效果較好。

4)如果改變保溫層使用材質，如采用“新型納米硅反射材料”，其理化指標見表5。該種材料每張厚度為10 mm，與石棉氈一樣，砌包結束后的實際厚度<10 mm。

模擬結果顯示，其10 mm～15 mm使用厚度的保溫效果就能滿足相當于石棉氈20 mm以上使用厚度的保溫效果(如圖8所示)。

表5 新型納米材料隔熱板主要理化指標

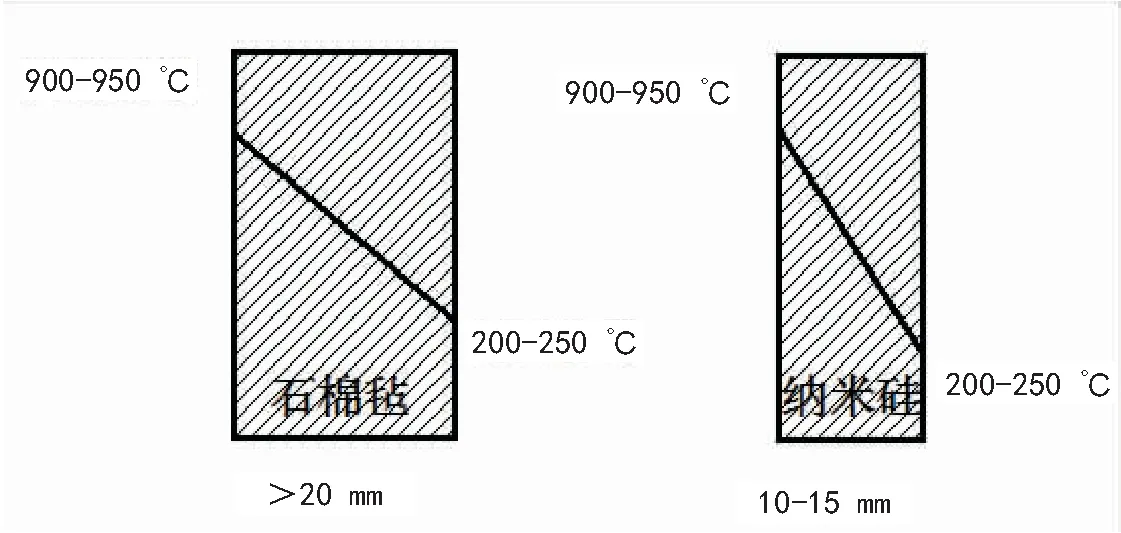
2.4 中間包覆蓋劑(材質與厚度)輻射及對流熱損失

某鋼廠3#鑄機要求中間包覆蓋劑厚度≤100 mm，但實際所用的材質均為廢舊的保護渣或認為不太好用的保護渣材料，并未采用雙層覆蓋劑方式：下層為堿性覆蓋劑熔融結構，主要吸附夾雜用；上層為保溫隔熱層(為避免中間包包蓋另加隔熱層)；但實際覆蓋厚度無定值，多為20 mm左右。

因此，以下就連澆爐次渣面溫度1 000 ℃(現用中間包覆蓋劑條件下)和渣面溫度為800 ℃(假設的采用雙層覆蓋劑后的渣面溫度)兩種情況下，對渣面熱損失做計算對比分析。

2.4.1 熱損失計算

中間包渣面熱量損失包括“輻射熱損失”和“對流熱損失”(這里假定為自然對流)，其中，包內氣氛溫度按tf=600 ℃設定，中間包渣面長度L=7.607 m，寬度W=1.183 m，黑度按ε= 0.6設定。可根據式(1)、式(2)進行計算。

q1=εCb((T/100)4-((tf+273)/100)4)·S

(1)

式中:q1——輻射熱，W；

ε——覆蓋劑表層黑度，這里取0.6；

Cb——黑體輻射系數，5.67，W·(m2·K4)-1；

T——覆蓋劑表層溫度(這里分別取1 000 ℃和800 ℃，即1 273 K和1 073 K，這兩個溫度取值即為式(2)中的tw的開氏溫度)，K；

tf——中間包包內氣氛溫度，℃。這里按600 ℃設定；

S——中間包渣面面積(由S=L×W計算確定)，m2。

q2= h(tw-tf)

(2)

式中:q2——對流熱，W；

h——覆蓋劑表層對包內氣氛的對流換熱系數，W·(m2·K)-1；

tw——覆蓋劑表層溫度，℃。這里分別取1 000 ℃和800 ℃；

tf——如式(1)中的說明。

其中，式(2)中關于h的計算則分別依據式(3)、式(4)、式(5)進行確定：

h=Nu·λ/l

(3)

式中:h——如式(2)中的說明；

Nu——努謝爾特準數，由式(4)計算確定；

λ——由定性溫度tm=(tw+tf)/2確定后查得的空氣的熱導率，W·(m·K)-1；

l——定型尺寸，m，由l = (L + W)/2計算確定。

Nu = C(Gr·Pr)n

(4)

式中:Nu——如式(3)中的說明；

Gr——格拉曉夫準數，由式(5)計算確定；Pr——普朗特準數，由定性溫度tm= (tw+ tf) /2確定后查得；

系數C、指數n——常數，由式(5)計算結果并參考表6確定。

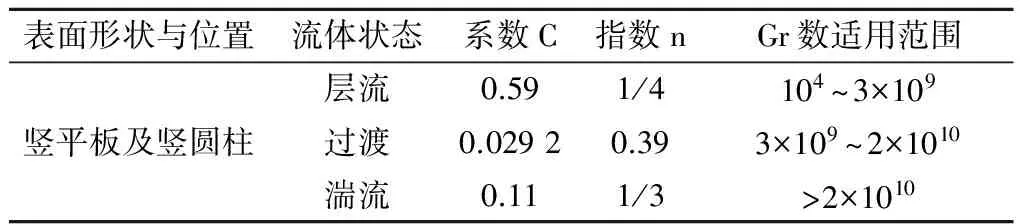
表6 典型表面形狀實驗室確定的常數C和n的取值表

Gr=βgl3Δt/ν2

(5)

式中:Gr——如式(4)中的說明；

β——格拉曉夫準數Gr中的體積膨脹系數，由β=1/(tm+273)計算確定；

g——重力加速度，這里取9.81m·s2；

l——如式(3)中的說明；

Δt——tw-tf的差值，℃；

ν——由定性溫度tm=(tw+tf)/2確定后查得的空氣的運動粘度，m2·s-1。

結合式(1) ～式(5)可分別計算渣面溫度T為1 000+273=1 273 K、800+273=1 073 K時中間包鋼水渣面熱量損失變化情況，計算結果見表7。

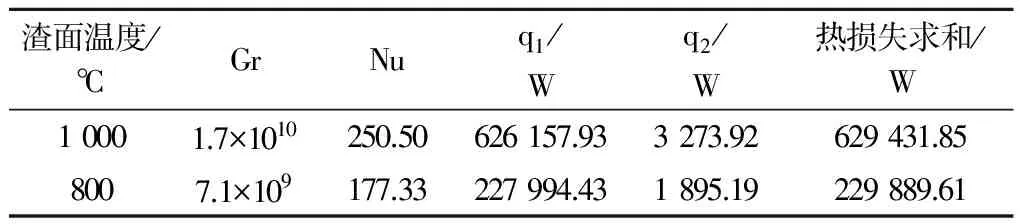
表7 中間包不同渣面溫度條件下熱損失計算結果

由表7數據可知，中間包渣面溫度800 ℃條件下總的熱損失約為渣面溫度1 000 ℃條件下的63%。

2.4.2 對鋼水溫度的影響

液態鋼水1 500 ℃的熱容按0.879 kJ·(kg·℃)-1計，中間包容量按5.3×104kg計。

根據上述計算可知，35 min內，上述兩種情況下損失的熱量分別為：1.51×106kJ、5.52×105kJ。那么，在包蓋各操作孔不完全隔熱封閉的情況下，約有30%～40%(前已述及包蓋各操作孔總面積約占包蓋平面面積的30%～40%)的渣層表面暴露于環境，這里取值30%。則在35 min內，依據公式(6)渣面散失的熱量可使中間包鋼水溫度下降值分別為：8.5 ℃和3.1 ℃。

Q=cmΔt

(6)

式中:Q——熱量，kJ；

c——鋼水的比熱容，kJ·(kg·℃)-1；

m——鋼水質量，kg；

Δt——溫差，℃。

以此推算，如果使用雙層覆蓋劑可使盛鋼量160 t的鋼包出站溫度下降3 ℃～5 ℃。這一點進一步說明了澆注過程中對中間包操作孔采取隔熱封閉的必要性。

綜上所述，渣面溫度僅降低200 ℃(從1 000 ℃降至800 ℃)的條件下對鋼水出站的溫度就有3 ℃～5 ℃的影響。可想而知，單就覆蓋劑而言，如果采用雙層覆蓋劑，則通過渣面造成的熱損失將大為降低。

2.5 包蓋加保溫層對中間包鋼水溫度的影響說明

現場砌包實際表明，中間包包蓋加保溫層(位置在鋼殼內側與鋼纖維澆注料之間)容易造成鋼纖維澆注料塌料事故，所以，這里不再進行包蓋加保溫層的熱模擬研究。

3 中間包溫降規律的數值分析

澆注過程中，普碳低合金鋼種在鋼水澆注溫度1 570 ℃、澆注周期按35 min計、中間包加蓋且有覆蓋劑等正常澆注條件的基礎上，計算了連澆3個包次的澆注過程中間包鋼水溫度變化規律，如圖9所示。

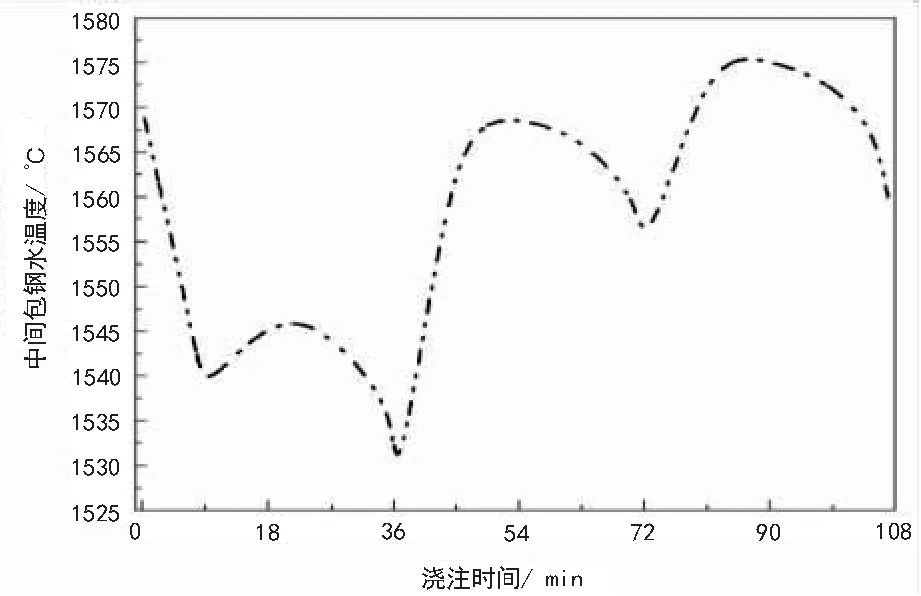
圖9 中間包鋼水溫降規律

計算所得中間包鋼液溫度變化規律與寶鋼實測中間包溫度變化規律相一致[6]。從圖9可以看出：

1)中間包內鋼液溫度變化很大，尤其是第1包次的澆注。第1包次鋼包開始澆注時包襯溫度較低，且在此期間內鋼液表面無任何覆蓋劑，鋼液自由表面直接向中間包空腔及環境輻射傳熱。

2)隨包襯蓄熱量不斷增加及隨后覆蓋劑等的加入很快達到熱平衡，中間包內鋼液溫度逐漸上升，由圖示曲線走勢可知，鋼液量澆注約1/2時達到最高。

3)在澆注中鋼包內鋼液的溫度逐漸降低，中間包內鋼液溫度也緩慢下降，但遠小于鋼液溫度上升時的速度。

4)更換鋼包時由于無新鋼液注入，包內鋼液面迅速下降，這時鋼液溫度下降速度明顯加快。當新的鋼包開澆后，鋼液迅速注入中間包，中間包內鋼液面很快恢復到正常澆注水平，由于新注入的鋼液溫度很高，中間包內鋼液溫度隨鋼液的注入而迅速上升且很快達到最大值，隨后緩慢下降，直到這一包次鋼液澆注結束，進入下一個包次循環。

5 結論

1)僅當鋼水較大面積暴露在環境中時，外界環境溫度的變化才顯著影響中間包鋼水溫度的變化。

2)可比條件下，澆注過程中間包操作孔“敞開”情況下對其鋼水溫度的影響超過了冬季相對較低的外界環境溫度對中間包鋼水溫降的影響程度。實際生產中應盡量減少中間包操作孔敞開的時間。

3)適當增加保溫層厚度對中間包的保溫效果有一定的影響。保溫層采用新型隔熱保溫材料將大幅改善中間包的保溫效果。

4)覆蓋劑的合理選用及正確使用有助于降低上鋼溫度，并改善中間包的過程溫降條件。

[1] 李里，周瑞和，薛念福，等. 攀鋼連鑄鋼包熱循環的現狀與分析[J]. 鋼鐵釩鈦，2002(3)：5-11.

[2] 譚真，郭廣文. 工程合金熱物性[M]. 北京：冶金工業出版社，1991：142-143.

[3] 楊世銘. 傳熱學基礎[M]. 北京：高等教育出版社，2004：18-30.

[4] 張朝暉，李樹奎. ANSYS11.0 有限元分析理論與工程應用[M]. 北京：電子工業出版社，2007：26-154.

[5] 胡紅軍，楊明波，張丁非. ANSYS10.0 材料工程有限元分析實例教程[M]. 北京：電子工業出版社，2008：54-176.

[6] 吳曉東，劉青，徐安軍，等. 寶鋼煉鋼廠300 t整體鋼包熱循環實測研究[J]. 北京科技大學學報，2001，23(5)：418-420.

NUMERICALANALYSISONTHEINFLUENCEFACTORSOFTHEHEATLOSSINTHECONTINUOUSCASTINGTUNDISH

Du Yawei Du Haiming Du Yulan Shan Qiang Su Bin

(Anyang Iron and Steel Group Co., Ltd)

2017—4—10

聯系人：杜亞偉，工程師，河南.安陽(455004)，安陽鋼鐵集團有限責任公司技術中心長材產品研究室；