BOOST交流斬波型無功補償器設計

王銀忠，牟憲民，許 康

（大連理工大學電氣工程學院，大連 116024）

BOOST交流斬波型無功補償器設計

王銀忠，牟憲民，許 康

（大連理工大學電氣工程學院，大連 116024）

針對交流斬波型無功補償裝置補償電流的各次諧波分量計算復雜，控制精度差等問題，本文以單相BOOST交流斬波型動態電容器為對象，建立了系統頻域模型，并提出局部靈敏度分析方法，采用基于同步參考坐標理論的閉環控制算法，實現了網側無功和諧波電流的閉環控制。相較于已有的數值計算模型，更加準確地分析了BOOST交流斬波電路占空比與無功補償電流、諧波電流之間的關系，系統性能和可靠性得到提高。仿真和實驗結果驗證了所提出的模型分析方法和控制算法的可行性及有效性。

交流斬波；BOOST電路；動態電容；無功補償；諧波抑制

Abstract:In order to solve the problems such as the computational complexity of each harmonic component of VAR compensator's compensation current based on AC chopper and the poor control precision，a frequency domain model of the system is established with a single-phase dynamic capacitor based on BOOST AC chopper as research object.A lo?cal sensitivity analysis method is presented，and the closed loop control of grid-side reactive power and harmonic cur?rent are realized using a closed-loop control algorithm based on the theory of synchronous reference coordinates．Com?pared with the existing numerical model，the proposed method can analyze the relationship between the duty cycle，reac?tive power compensation current and harmonic current more precisely，thus the performance and reliability of the sys?tem is improved．The feasibility and effectiveness of the proposed model and control strategy are validated through sim?ulation and experimental results.

Key words:AC chopper；BOOST circuit；dynamic capacitor；reactive power compensation；harmonic suppression

基于交流斬波電路的動態電容器D-CAP（dy?namic capacitor）是一種新型的動態無功和諧波補償技術。D-CAP與靜止無功補償器SVC（static VAR compensator）相比，成本相當，但其具有動態補償能力，響應速度也更快。D-CAP與靜止同步補償器STATCOM（static synchronous compensator）、并聯型有源濾波器APF（active power filter）相比，性能相近，由于不需要采用大容量的電解電容器作為儲能設備，成本更低廉，系統壽命更長，可靠性增強，因此其具有廣闊的市場前景[1-2]。

文獻[3-4]根據虛擬正交源理論，提出了基于Buck交流斬波結構的D-CAP概念，由于不采用逆變器結構，這樣就省去了大容量的直流儲能元件，并且采用不同的控制方法可以同時實現無功補償和諧波抑制功能。文獻[5-7]提出有源阻抗理論，采用交流斬波電路控制電感或電容進而向電網注入可控無功電流，與文獻[3-4]基本思想相同。文獻[8]以單相Buck型交流斬波無功補償器為研究對象，提出了直接電流閉環控制策略，但未提及諧波控制方案。文獻[9]提出了三相三線制BOOST交流斬波型有源濾波器概念，實現了無功和諧波的動態補償，但其針對三相對稱系統，對單相和三相不平衡供電系統未做研究。以上研究多針對Buck型交流斬波電路，其無功和諧波電流與占空比的關系式可準確獲得[10]，而對于BOOST和Buck-BOOST等其他拓撲則很難獲得。已有的研究使用數值計算方法給出了粗略的定量計算結果，分析了開環給定補償電流的方法，實驗中雖采用閉環控制方法，但是在控制過程中產生大量不可控的額外諧波，并未取得良好的控制效果。

本文針對單相BOOST交流斬波型D-CAP，詳細分析了BOOST交流斬波模塊的基本原理和補償特性，建立了系統的頻域模型，提出局部靈敏度分析方法，定性和定量分析了占空比與無功補償電流及諧波電流的對應關系，采用基于同步坐標理論的閉環控制算法，使系統實現了無功和諧波的閉環控制。與現有的分析方法相比，本文提出的局部靈敏度分析方法，更好地解決了BOOST交流斬波型DCAP的無功和諧波補償精度受限問題，獲得了較好的補償效果。

1 BOOST交流斬波D-CAP工作原理

BOOST交流斬波器使用雙向開關代替直流斬波電路中的單向開關，如圖1所示。雙向開關K1、K2采用共射極反向串聯的絕緣柵雙極型晶體管IGBT（insulated gate bipolar transistor）組成，Lf和Cf組成的網側LC低通濾波器濾除開關器件產生的高頻諧波，RL1和RL2是寄生電阻。斬波器二次側帶電容負載C，通過對交流斬波電路的控制可使其向網側注入可控的無功和諧波電流。

圖1 基于BOOST交流斬波器的動態電容器Fig.1 D-CAP based on BOOST AC chopper

與直流BOOST斬波電路相似，BOOST交流斬波電路也具有升壓功能，輸出電壓[11-12]為

式中：us（t）為電源電壓；iC（t）為流過電容C上的電流；d（t）為雙向開關K1的占空比，1-d（t）為K2的占空比。

1.1 恒定占空比調制

假設電網電壓為us(t)=Ussin(ωt)，當占空比d（t）為恒定常數D0時，流過電容上的電流為

無功補償電流為

式中，ω為電網電壓基波角頻率。

由式（3）和式（4）可知，BOOST交流斬波無功補償器向電網注入容性的補償電流，可將其看作容值連續可調的D-CAP。由于電網電壓幅值Us、基波角頻率ω和無功補償電容C為恒定值，因此改變占空比D0的大小便可改變向電網中注入電流的大小，從而實現網側無功的連續可控調節。

1.2 偶次諧波調制

為了消除晶閘管整流器等非線性負載產生的諧波，可以向電網中注入與這些諧波大小相等、方向相反的諧波電流，從而實現有源濾波。單相非線性負載產生的多為3、5、7等奇次諧波，當向占空比中加入偶次諧波調制項EHM（even harmonic modu?lation）時，則有

式中：Dn為第n次EHM的幅值，0≤D0+D2+D4+…+Dn≤1，n為正偶數；φn為第n次EHM的初相角。

以向占空比中加入第n次偶次諧波調制項為例，此時占空比d（t）為

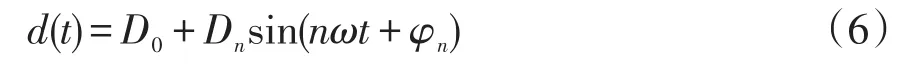
流過電容上的電流可表示為

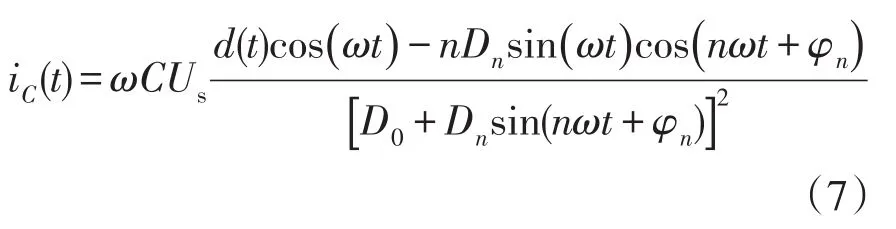
補償電流可表示為

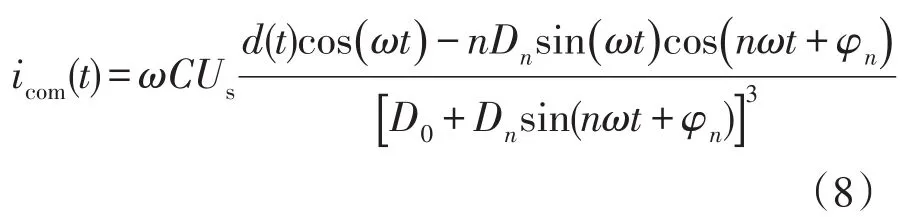
由上述分析可知，在占空比中加入第n次EHM時，系統向電網注入電流中含多個奇次諧波分量，由于各EHM產生的諧波電流會發生交叉耦合，這無疑增大了調制難度。由于BOOST交流斬波電路的非線性特性，而且電流計算公式中占空比位于分母位置且是變量，當加入多個EHM時，要得到icom（t）的傅里葉分析式便更加困難。本文建立了系統的頻域模型并利用局部靈敏度分析方法，準確地得到EHM與各奇次諧波的對應關系。

2 分析方法

2.1 頻域模型

為精確地分析占空比與無功和各次諧波電流的對應關系，建立了系統的頻域模型。由于輸入LC低通濾波器只濾除開關頻率附近高頻諧波，為簡化分析，將其省略，則單相BOOST交流斬波型DCAP的頻域模型如圖2所示。

圖2 D-CAP頻域模型Fig.2 Frequency-domain model of D-CAP

其中，YRL為圖1中濾波電感L和寄生電阻RL2的串聯導納矩陣，ZC為電容C的阻抗矩陣，T為交流斬波電路對應的矩陣。YRL、ZC可分別采用二端口網絡理論求得，即

其中

式中：yRL(n)為L與RL2的串聯導納，yRL(n)=1/(R+ j100πnL)；ZC(n)為電容C的阻抗，ZC(n)=-j/(100πnC)；N為子矩陣的階數。

矩陣T的推導過程如下。

占空比中含各次EHM，以正弦和余弦的形式給出，即

當網側電壓中的第h次諧波u(hωt)乘以第g次偶次諧波調制項d(gωt)得

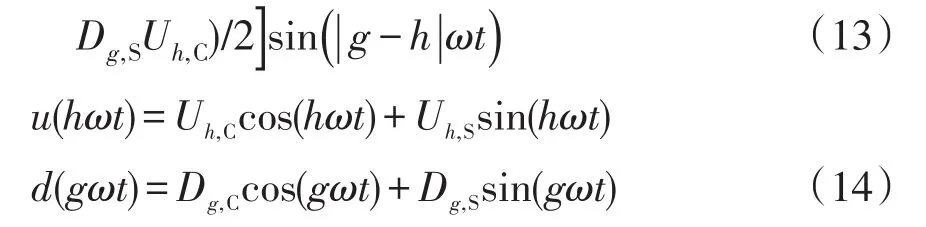
式中：g=2k-2；k∈[1,2,3,???,NE]；h=2n-1；n∈[1,2,3,???,NH]；NE為EHM的個數；NH為奇次諧波個數。

式（13）可表示任意EHM和電壓諧波的乘積。所有諧波和EHM乘積的總和為

網側電壓us（t）作為輸入變量，將其時域模型中的傅里葉系數組成一維矩陣U，ω(t)作為輸出變量，其各項傅里葉系數也可組成一維矩陣W，而交流斬波電路可由方陣T表示，可得其頻域模型為

式中：矩陣U和W均為一維矩陣，且具有相同的列數；T的階數與U的列數相同。

矩陣的推導過程中并未將實際的傅里葉系數在矩陣中寫出，而是用“+”“－”表示。對應的傅里葉系數在矩陣下方標出，這樣可以更直觀地觀察傅里葉系數在矩陣中的位置和大小。矩陣由4個子矩陣組成，即

矩陣T的階數由EHM和考慮到的諧波次數決定，其對應關系為

每個子矩陣關于主對角線對稱，占空比中加入2次諧波調制項時，各子矩陣的推導形式為

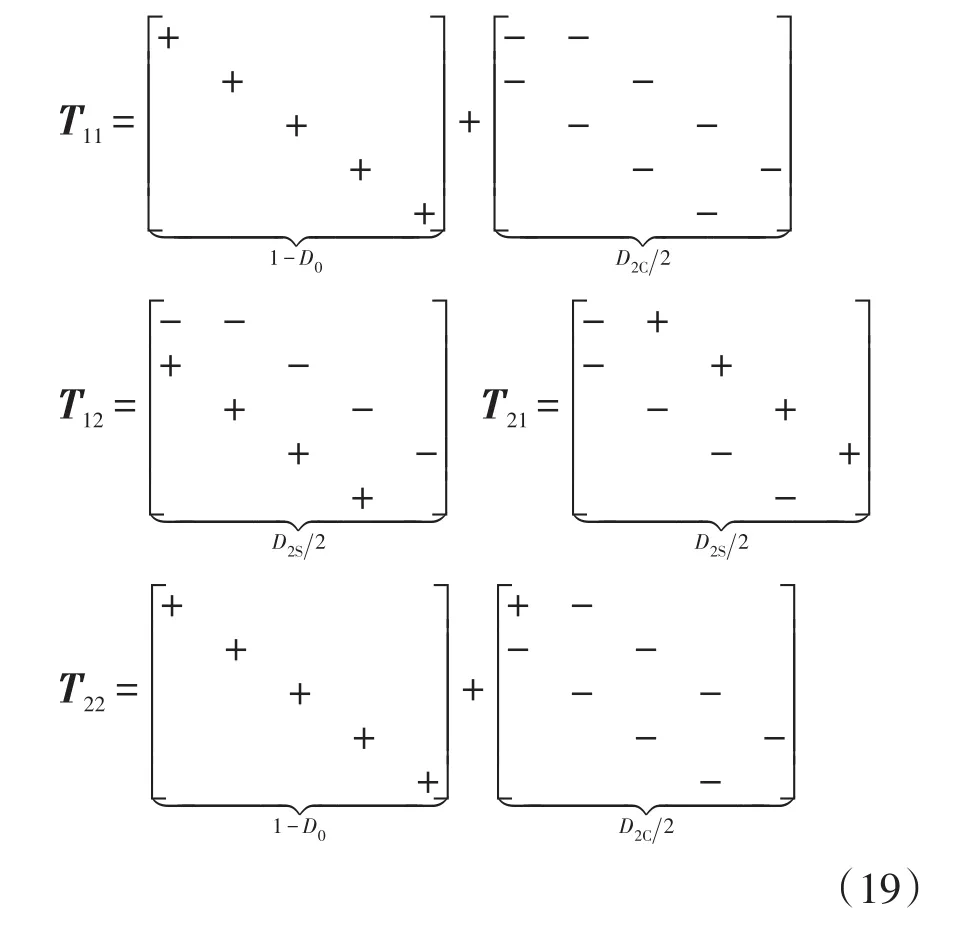
式中：T11和T22含常數項和二次諧波調制項；T12和T21僅含第2次EHM，“+”、“－”所在位置的值為矩陣下方的系數，正負性與“+”、“－”一致。根據推導公式的明確特征，可很容易將推導過程擴展到加入2、3、4等多個偶次諧波調制項的情況。

容易得到網側電壓的傅里葉分析式為

式中：an為傅里葉展開式sin項的幅值；bn為傅里葉展開式cos項的幅值。

因此，網側電壓可表示為一維矩陣，即

式中：U1C～UnC和U1S～UnS分別為網側電壓傅里葉展開式的cos項和sin項幅值系數；下標C和S表示余弦項和正弦項。

系統的無功補償電流為

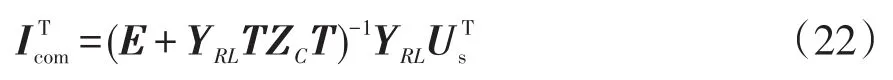
由以上分析可知，在系統確定的情況下，矩陣Us、YRL、ZC便可確定，而矩陣T在需要消除的諧波確定的情況下也可確定，因此可得到補償電流矩陣Icom，其由基波和各奇次諧波的cos項和sin項幅值構成。從而可知EHM與系統補償電流各奇次諧波幅值具有明確的定量關系。

由于非線性負載產生諧波多為奇次諧波，且隨著次數的增大，諧波幅值減小，即

為獲得最大的調節范圍而且占空比0≤d(t)≤1，通常將占空比的D0取0.5，各EHM的幅值取前一項的1/3，將占空比以矩陣形式表示為

式中：n為對應的EHM偶數次數；DnC和DnS分別為占空比第n項余弦項和正弦項的幅值。以網側電壓為220 V，濾波電感和補償電容分別為2.5 mH、25 μF，寄生電阻為0.1 Ω，占空比加入2次EHM為例，占空比d=[0.5 0.05 0.05]。此時可根據式（13）得到精確的系統補償電流為

其中前5項為余弦項系數，后5項為正弦項系數。

圖3中為根據頻域模型得到的補償電流的基波和諧波幅值隨D2和D4的變化關系曲線（此時D0=0.5，D2=0～0.167，D4=0～0.056）。隨著D2增大，補償電流的基波分量和各次諧波分量增大，且3次諧波幅值變化較大，與D2大致呈線性關系，7次諧波在D2取值0.1之后幅值迅速增大，在（0.1～0.168）范圍內不可忽略，5次諧波和9次諧波幅值相對于3次諧波始終較小。隨D4增大，基波分量和3、7、9、11等諧波分量略有增大但幅值較小（小于1 A），而5次諧波電流與D4呈線性關系，因此可以D4來抑制電網中的5次諧波。

圖3 EHM與諧波電流關系Fig.3 Relationship between EHM and harmonic current

2.2 靈敏度分析

頻域模型得到了補償電流各奇次諧波和占空比的定量關系，采用局部靈敏度分析方法研究各EHM系數和補償電流各奇次諧波的定性關系，常數項D0主要用來產生超前的無功補償電流，為分析方便，忽略對D0的分析。

補償電流Icom分別對占空比各EHM的正余弦項幅值求導，將其定義為補償電流相對于占空比各EHM的cos和sin項系數的靈敏度，可得

式中，x=2C,2S,4C,4S,???,nC,nS。

由于占空比0≤d(t)≤1，因此行向量d滿足

同樣以第2.1節中的系統為例，占空比加入第2次EHM，且EHM的cos和sin項取值相同，d=[0.5 0.05 0.05]。圖4中分別表示補償電流各次諧波相對于第2次EHM的cos項（D2C）和sin項系數（D2S）的敏感度，柱形圖的幅值越大，表明對應的諧波電流對于相應的EHM的靈敏度越大。

由圖4可得到EHM和諧波電流的定性關系，第n次諧波電流對第n-1次EHM的參數變化最敏感。因此可用第n-1次EHM控制補償電流中的第n次諧波電流，且第n次諧波電流的cos系數對第n-1次EHM中的cos系數靈敏度較大，第n次諧波電流的sin系數對第n-1次EHM中的sin系數靈敏度較大。同時，改變某一EHM時，多個次數諧波電流靈敏度較大，即補償電流中的各次諧波電流之間會發生交叉耦合。因此，改變占空比中的任一項系數，都會影響補償電流中的多次諧波，這增大了諧波電流控制的難度。在設計各次諧波電流的控制路徑時，為阻止不同次數的諧波電流之間的交叉耦合，可對臨近的諧波電流設計不同的時間常數，使不同的控制路徑調節速度不同。因此，較快的路徑可以補償較慢的路徑耦合產生的變化，這就為各次諧波的閉環控制提供了可能。

圖4 二次EHM靈敏度分析Fig.4 Sensitivity analysis of the second EHM

3 單相BOOST型D-CAP控制策略

由前述的結論可知，當向占空比中加入2、4、6等偶次諧波調制項時，可以用來補償非線性負載產生的第 3、5、7等奇次諧波。由于占空比0≤d(t)≤1，為保證占空比在0～1之間變化，占空比的常數項D0必不可少。

本文采用基于同步參考坐標理論無功和諧波電流檢測方法，應用直接電流控制策略，實現無功和諧波的閉環控制。由圖5可知，首先采樣電網電流，采用延遲90°的方法將電網電流進行正交分解，得到兩個相互垂直的電流分量iα（與電網電流同相）和iβ（滯后電網電流90°）。第1個路徑是對基波無功電流進行檢測與控制，對基波角頻率分量進行Park變換，得到d軸分量id和q軸分量iq（相當于電網電流無功分量），將iq與0做差，差值經過PI環節后得到調節無功的恒定占空比D0。與無功控制路徑類似，其他的路徑是對諧波進行控制。采用各奇次諧波對應的角頻率進行Park變換，然后將變換后的分量通過PI環節進行調節，再進行Park反變換形成消除諧波對應的EHM。由于第n個EHM主要消除第（n+1）次諧波，因此Park逆變換對應的角頻率比正變換對應的角頻率小ω，最后將變換后的結果相加即可得到占空比d（t）。將占空比d（t）進行脈沖寬度調制PWM（pulse width modulation），可得到BOOST交流斬波電路的開關信號。

圖5 無功和諧波閉環控制Fig.5 Close-loop control for VAR and harmonics

4 仿真和實驗

為驗證單相BOOST型D-CAP的無功和諧波補償特性，搭建了Matlab/Simulink仿真模型。其中，網側電壓us為220 V，濾波電感L和補償電容器C分別為2.5 mH和25 μF，阻感負載L1、C1分別為15 Ω、50 mH，非線性負載L2、C2、R2分別為10 mH、330 μF、100 Ω，低通濾波器Lf、Cf為2.2 mH、20 μF，電路帶阻感負載并聯非線性負載，網側電流滯后電壓，功率因數為0.82，且電流有畸變，總諧波失真THD（total harmonic distortion）為18.89%。當采用圖5中的第1、2、3、4條控制路徑時，系統向電網中注入了與非線性負載產生的諧波電流大小相等、方向相反的第3、5、7等次數的諧波電流，使THD降為4.26%，圖6（a）和圖6（b）為補償前后網側電流THD。由于占空比中含有偶次諧波調制項，不再是恒定常數，而是隨時間有規律地變化。再加上占空比中常數項的作用，補償后網側電流和網側電壓同相位，功率因數變為1，補償電流波形、補償后網側電壓和電流波形如圖6（c）和圖6（d）所示。

圖6 偶次諧波調制仿真波形Fig.6 Simulation waveforms under EHM

為進一步驗證系統模型和控制策略的正確性，搭建了圖1所示的實驗電路，實驗采用DSP28335作為控制芯片，功率開關采用仙童公司的G60N100型 IGBT反向串聯組成雙向開關，實驗電源由BK-1000型變壓器提供（輸出電壓為24 V），阻感負載取為10 Ω、20 mH，非線性負載與仿真參數相同，開關頻率為10 kHz。使用TDS3032B示波器中的快速傅里葉變換FFT（fast Fourier transformation）計算功能測量補償電流頻譜。

由圖7可知，補償電流為超前電網電壓90°的容性補償電流，補償前網側電流含3、5、7等奇次諧波，實驗中采用了如圖5所示的控制策略的第1、2、3條控制路徑，這些控制路徑是將占空比加入了D0、D2和D4。由圖7（a）和（b）可知，網側電流中的第3、5次諧波電流得到了補償，網側電流與電壓實現了同相位，且補償效果沒有受到第2條和第3條控制路徑交叉耦合的影響。通過搭建仿真模型和實驗電路，驗證了頻域模型、靈敏度分析模型的可行性和閉環控制策略的有效性。

圖7 偶次諧波調制實驗波形Fig.7 Experimental waveforms under EHM

5 結語

基于單相BOOST交流斬波器的D-CAP作為一種動態無功和諧波補償方案，通過對交流斬波電路的控制，可同時實現電網功率因數校正和諧波抑制功能。針對占空比中各偶次諧波調制項產生的諧波會發生交叉耦合，調制難度大的問題，建立了系統的頻域模型，推導出占空比與無功補償電流和各次諧波電流的定量關系，提出靈敏度分析方法，得到了補償電流中各次諧波和占空比各諧波調制項的一般性對應關系。基于同步參考坐標理論的閉環控制算法使系統可以實時、快速、精確地補償無功和諧波電流，仿真和實驗驗證了分析模型和控制策略的可行性和有效性。

[1]Prasai A，Sastry J，Divan D M.Dynamic capacitor（DCAP）：An integrated approach to reactive and harmonic compensation[J].IEEE Trans on Industry Applications，2010，46（6）：2518-2525.

[2]馬瑞軍，王輝云，常鮮戎，等（Ma Ruijun，Wang Huiyun，Chang Xianrong，et al）.DSTATCOM的新型高補償精度檢測方法（Novel detection method for DSTATCOM with high compensation precision）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2015，27（10）：62-68.

[3]Prasai A，Sastry J，Divan D.Dynamic var/harmonic com?pensation with inverter-less active filters[C]//IEEE Indus?try Applications Society Annual Meeting.Edmonton，Can?ada，2008.

[4]Prasai A，Divan D.Control of dynamic capacitor[J].IEEE Trans on Industry Applications，2011，47（1）：161-168.

[5]Ladoux P，Lowinsky A，Marino P，et al.Reactive power compensation in railways using active impedance concept [C]//International Symposium on Power Electronics，Elec?trical Drives，Automation and Motion.Pisa，Italy，2010：1362-1367.

[6]Raimondo G.Power quality improvements in 25 kV 50 Hz railway substation based on chopper controlled impedanc?es[R].Toulouse Inpt，2012.

[7]Ladoux P，Fabre J，Caron H.Power quality improvement inacrailwaysubstations：Theconceptofchopper-controlled impedance[J].IEEE Electrification Magazine，2014，2（3）：6-15.

[8]武偉，謝少軍，湯雨，等（Wu Wei，Xie Shaojun，Tang Yu，et al）.基于Buck交-交斬波器的無功補償器拓撲與控制方法設計（Topology and control strategy design for buck AC-AC chopper based var compensators）[J].電力系統自動化（Automation of Electric Power Systems），2013，37（5）：124-129.

[9]Liu Quanwei，Deng Yan，He Xiangning.BOOST-type in?verter-less shunt active power filter for VAR and har?monic compensation[J].IET Power Electronics，2013，6（3）：535-542.

[10]李楚杉（Li Chushan）.基于虛擬正交源電壓合成策略的直接AC-AC變換拓撲與控制技術研究（Research on To?pologies and Control of Virtual Quadrature Source Based Direct AC-AC Power Conversion）[D].杭州：浙江大學電氣工程學院（Hangzhou：College of Electrical Engineer?ing，Zhejiang University），2014.

[11]Raimondo G，Ladoux P，Lowinsky A，et al.Reactive power compensation in railways based on AC boost choppers[J].IET Electrical Systems in Transportation，2012，2（4）：169-177.

[12]Liu Quanwei，Deng Yan，He Xiangning.A novel AC-AC shunt active power filter without large energy storage ele?ments[C]//Proceedings of the 14th European Conference on Power Electronics and Applications.Birmingham，UK，2011.

Design of VAR Compensator Based on BOOST AC Chopper

WANG Yinzhong，MU Xianmin，XU Kang
（College of Electrical Engineering，Dalian University of Technology，Dalian 116024，China）

TM76

A

1003-8930（2017）09-0129-07

10.3969/j.issn.1003-8930.2017.09.021

2016-03-01；

2017-05-27

王銀忠（1990—），男，碩士研究生，研究方向為電力電子與電力傳動。Email：halo_wang@126.com

牟憲民（1973—），男，博士，副教授，研究方向為電網無功補償、電力電子技術。Email：muxm@dlut.edu.cn

許 康（1992—），男，碩士研究生，研究方向為電力電子與電力傳動、水下無線電能傳輸。Email：277758036@qq.com