把握本質區別 明確兩類計算
(安徽省碭山中學,安徽 碭山 235300)
把握本質區別明確兩類計算
邵永
(安徽省碭山中學,安徽 碭山 235300)
全面理解和把握教材,深入挖掘教材,利用基本知識、方法和思想,從非靜電力的提供和感應電動勢的公式兩個方面區分感生電動勢和動生電動勢,理解兩種電動勢的來由、區別和聯系,既提高了學生的理性思維能力和追根問底、格物致知的思維習慣,又加深了對所學知識的深刻理解,明確兩類常見的計算。
感應電動勢;動生電動勢;本質區別
1 引言
在“電磁感應”的教學中,由于高中生在電磁場的理論知識和數學知識兩方面都存在不足,因此學生未能做到深究,未能從本質上區分感生電動勢和動生電動勢,從而造成在相關的計算中經常出錯,疑問重重。而實際上人教版2003年新課標教材較老教材做了許多改動,從電磁感應現象、本質、規律三方面進行闡述,如果我們能深挖教材,利用基本知識、方法和思想,完全可以從本質上區分兩種電動勢。
2 感生電動勢與動生電動勢的區別
2.1 從非靜電力角度區分兩種電動勢
在人教版教材19頁中這樣說道:電路中電動勢的作用實際上是某種非靜電力對自由電荷的作用。對于不同電源,非靜電力來源也不同。區分感生電動勢和動生電動勢時,可從此入手。
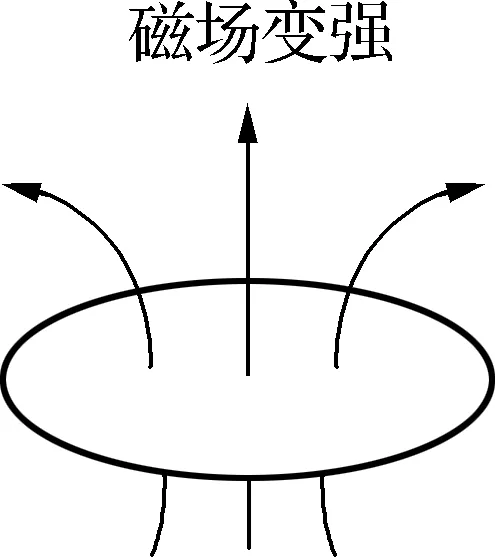
圖1
圖1是教材中原圖,描述的是一個閉合電路靜止于磁場中,由于磁場強弱的變化,在此空間產生是否存在閉合導體無關的感生電場。如果存在閉合導體,導體中的自由電荷就會在感生電場的作用下定向移動,在這種情況下,所謂的非靜電力就是感生電場對自由電荷的作用。
如圖2所示,金屬桿ab以速率v向右平移,它里面的電子也隨之向右運動,向右運動的電子因處在磁場中,要受到洛倫茲力作用,由左手定則可以判斷洛倫茲力方向向下,沿桿的洛倫茲力驅使自由電子向下運動,閉合線框中便出現逆時針方向的電流,這樣在桿ab中就產生了感應電動勢,又由于自由電子沿桿向下運動,由左手定則可以判斷電子受到向左的洛倫茲力,所以這時的非靜電力是洛倫茲力沿桿的分力。
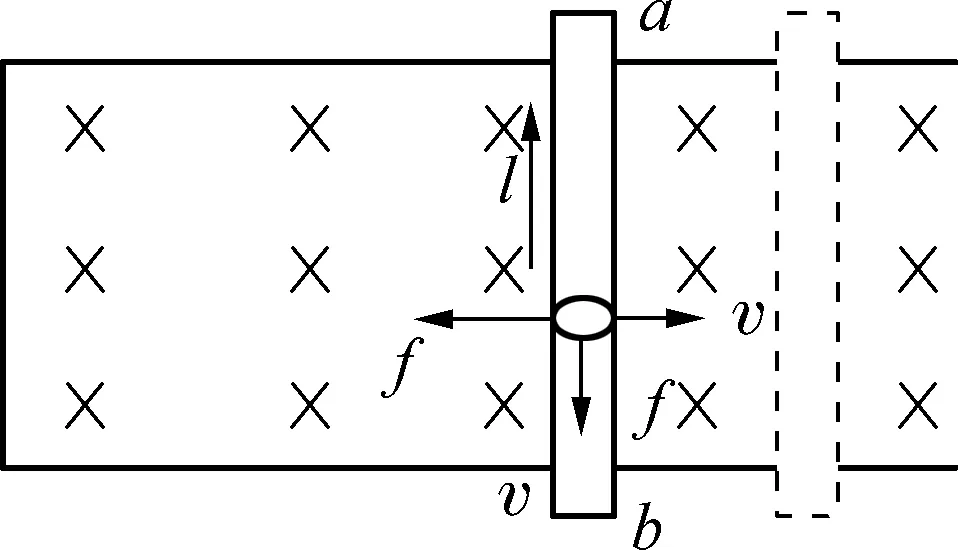
圖2
2.2 從感應電動勢的公式區分兩種電動勢
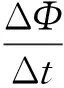
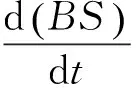
3 明確兩類計算
3.1 克服安培力做功的功率是否總等于回路中消耗的功率
例1:如圖3所示,兩條足夠長、相距為d的光滑水平導軌,其單位長度的電阻為r,左端MN用阻值不計的導線相連,電阻不計的金屬棒ab可在導軌上滑動。整個裝置處于豎直向下的均勻磁場中,金屬棒ab在水平外力的作用下,以速度v沿導軌向右做勻速運動,t=0時,金屬棒ab與MN相距非常近。
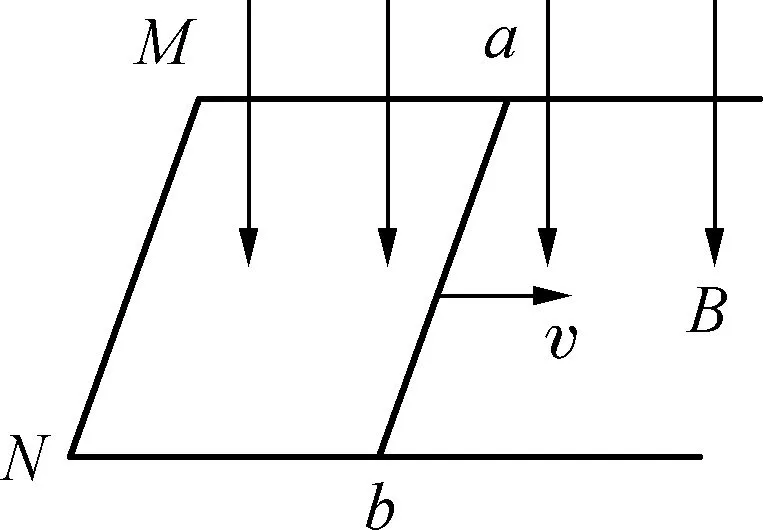
圖3
(1) 如果在此空間加一磁感應強度為B=kt0的勻強磁場,求t=t0時刻閉合回路消耗的功率。
(2) 如果在此空間加一磁感應強度隨時間均勻增加,B=kt的磁場(其中k為常數),求t=t0時刻閉合回路消耗的功率。

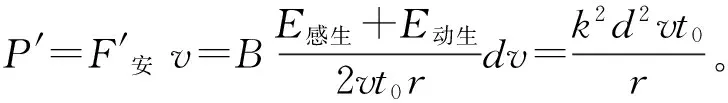
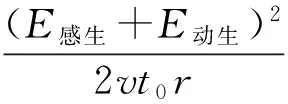
釋疑:在第(1)問中只存在動生電動勢,由圖2可知洛倫茲力沿桿的分力f充當非靜電力,而洛倫茲力的另一個分力f′宏觀上表現為安培力,又由于洛倫茲力不做功,所以洛倫茲力沿桿的分力所做的功等于克服安培力F安的功,即電路中消耗的功率等于克服安培力的功率,所以第(1)問的計算是正確的。由于感生電動勢的產生原因是感生電場力充當非靜電力,所以在第(2)問中既存在感生電動勢又存在動生電動勢,雖然非靜電力f的大小與感生電動勢無關,但是當增加了感生電動勢后,自由電荷沿桿的速度v′會發生變化,這樣會使f′發生變化,宏觀上表現為安培力發生了變化。由于本題在t=t0時刻動生電動勢與感生電動勢大小和方向均相同,所以自由電荷沿桿的速度v′和F安均增大為原來的2倍,所以克服安培力做功功率F安v與非靜電力f做功功率fv′仍相等,且變為原來的2倍,所以錯解中計算的僅是非靜電力f的功率,如果加上感生電場力的功率,就變為原來的4倍。
綜上所述,可總結出以下結論:(1) 由于洛倫茲力總是不做功的,所以安培力(洛倫茲力的分力f′的宏觀表現)的功率只是對應充當非靜電力的f的功率,所以在只存在動生電動勢時,才能用克服安培力的功率計算電路消耗的功率。
(2) 兩種電動勢同時存在時,雖然每一種電動勢都不影響另一種電動勢的非靜電力,但影響了非靜電力做功功率的另一個因素——沿桿的定向移動速度。
3.2 在B隨x變化的磁場中做切割磁感線運動時是否同時存在兩種電動勢
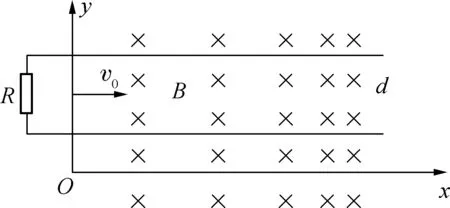
圖4
例2:如圖4所示,兩根相距為d的足夠長光滑的平行金屬導軌位于水平xOy平面內,一端接有阻值為R的電阻,其它電阻均忽略不計,在x>0的一側存在沿豎直方向的磁場,磁感應強度B的大小隨x的增大而增大,滿足B=kx,式中的k是常量,一根金屬直桿與金屬導軌垂直,可在導軌上滑動,當t=0時位于x=0處,速度為v0,方向沿x軸的正方向。在運動過程中,有一大小可調節的外力F作用于金屬桿上以保持金屬桿的加速度恒定,加速度大小為a,方向沿x軸負方向,求:
(1) 該回路中的感應電流持續的時間是多長?
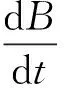
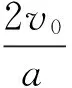
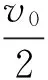
綜上所述,教材是教師教學、學生學習主要依據,是學生獲取知識、提升能力的主要資源,在教學中應深入理解教材、挖掘教材,重視教材中的基礎知識、方法和思想,在解決問題的過程中達到對物理知識與方法的融會貫通。

