基于隨機減量法的分布式結構模態參數識別

逯靜洲, Sung Han Sim, Billie F.Spencer, Jr.

(1. 煙臺大學 土木工程學院,山東 煙臺 264005； 2. 蔚山科學技術大學 城市與環境工程學院，韓國 蔚山 44919； 3. 伊利諾伊大學 香檳分校 土木與環境工程系, 美國 61801)

基于隨機減量法的分布式結構模態參數識別

逯靜洲1, Sung Han Sim2, Billie F.Spencer, Jr.3

(1. 煙臺大學 土木工程學院,山東 煙臺 264005； 2. 蔚山科學技術大學 城市與環境工程學院，韓國 蔚山 44919； 3. 伊利諾伊大學 香檳分校 土木與環境工程系, 美國 61801)

分區進行平行分析處理的技術已成為大型結構密集布置無線智能傳感器網絡檢測結構系統的重要任務。提出基于隨機減量法的分布式數據采集和模態識別方法。以兩邊簡支板模型試驗為例，采用ISM400無線智能傳感器，通過自然激勵法獲得測試結構的響應信號，計算隨機減量函數，然后運用特征系統實現算法提取系統的狀態空間參數，并結合穩定圖的方法剔除虛假模態，識別出結構的模態性能參數。以模態置信度為判據對比分析分布式算法與集中式算法的識別效果，結果表明兩種算法吻合良好。

隨機減量法；分布式傳感器網絡；特征系統實現算法；穩定圖；模態識別

近20年來，基于無線智能傳感器網絡的結構健康監測系統研究逐漸取得工程界的認同，并開始用于重大工程結構中。振動測試時需要布置中央處理器(也稱基站或網關)和傳感器(也稱節點)。傳統的集中采集和處理數據技術，每個節點都直接把數據傳遞給基站，節點只負責數據采集，基站則負責數據的處理。這種方法雖然簡便易行，但受到帶寬、數據擁堵和耗能等原因的限制，這種方法對于無線傳感器顯得效率不高。為此，基于局部數據聚合和壓縮技術的協同分布式采集方法應運而生，這種方法不僅避免傳遞冗余無用的數據，而且節省時間和能耗，效率明顯提高[1]。Nagayama等[2]提出分散數據聚集(Decentralized Data Aggregation，DDA)方法，這是一種分層次的數據采集處理方法，可將傳感器分成三個層次：基站、簇頭和節點。協同分布式采集主要分成以下三步：一是每個節點同步獨立采集數據；二是在組層次的局部數據通訊和處理，即在組內各個節點與簇頭進行數據傳遞和處理，通過局部傳感器網絡之間的交流合作獲得有價值的信息，例如得到相關函數等；三是由簇頭把有價值的信息傳遞給基站。這種方法中不需要每個節點都與基站直接進行數據傳遞，可以減少數據傳遞所需要的時間和電池能量，而且因為各個組之間有重疊，很好的保證了傳感器之間相對的空間信息不致丟失。DDA方法能最好地配合密集布排的智能傳感網絡，充分發揮其效能，真正實現足尺結構的現代健康監測。但目前基于分布式無線智能傳感器網絡結構模態識別的研究比較有限，且由于缺乏必要的試驗驗證，推廣應用很少。

環境激勵下結構的模態參數識別是結構健康監測研究的關鍵，它屬于工作狀態模態分析，可以不暫停結構的正常使用，這極大的方便了結構在正常使用狀態下健康監測工作的進行[3]。隨機子空間方法可以從環境激勵響應中直接提取結構自由衰減信號進行在線模態參數識別，與傳統的頻域系統識別方法相比，該法不但能準確地識別系統的頻率，還能很好地識別系統的模態振型和阻尼，識別結果更加精確[4]。張敏等[5-6]基于隨機子空間法提出分布式模態參數識別方法，并利用粒子群優化算法和平均技術調整子結構振型，獲得結構的整體振型，與集中式算法結果對比發現，該分布式算法應用靈活，可用于不同情況的子結構網絡拓撲結構，具有良好的識別效果。但是隨機子空間方法對非平穩信號的處理有時顯得無能為力。隨機減量法是由Cole[7-8]首先提出的，是指從線性振動系統的一個或多個平穩隨機響應樣本函數獲得系統自由振動響應的數據處理方法。其基本思想是在線性系統的疊加原理基礎上，利用測量的響應信號構造出表征結構自由振動的響應信號，即表征結構特性的一個自由衰減信號[9]。隨機減量法改進后則可直接處理零平均值非平穩響應信號，得到自由衰減響應[10-11]。Sim等[12]則基于隨機減量法提出一種分布式模態參數識別方法，并將其應用于無線傳感器，在桁架模型振動模態識別試驗中得到驗證。但基于環境激勵的分布式模態參數識別方法仍有待于深入研究，這是采用無線傳感網絡的健康監測系統分布式計算的基礎。

本文將在以上研究的基礎上，重點研究基于隨機減量法的分布式數據采集和模態識別方法，并通過實驗驗證該方法基于板類連續結構的響應信號計算整體模態信息的適用性，并與集中式算法獲得模態信息進行對比分析。

1 基本原理

1.1隨機減量法基本原理

隨機減量法是指從線性振動系統的一個或多個平穩隨機響應樣本函數獲得該系統自由振動響應，將自由振動響應表達為一解析形式，建立準則函數，調整解析函數中的參數，使準則函數取極小值，通過牛頓-拉夫遜迭代法獲取模態參數的最優估計值，獲取大型結構環境激勵下的模態參數[13]。Vandiver等[14]于1982年首先明確指出，在滿足高斯分布、均值為零的隨機過程這一個特定情況下，隨機減量函數正比于相應隨機信號的自相關函數。Brincker等[15]則根據一般形式的觸發條件推導出了隨機減量函數與相應相關函數之間更一般性的數學關系。隨機減量法的核心是利用在隨機激勵下系統的響應信號構造一個系統的自由振蕩信號，即系統的一個齊次解。

對于線性系統，設X1(t)與X2(t)為滿足均值為零的高斯分布的隨機響應樣本，則X1(t)與X2(t)按觸發條件CX1(ti)的自相關和互相關隨機減量函數為

DX1X1(τ)=E[X1(ti+τ)|CX1(ti)]

(1)

DX2X1(τ)=E[X2(ti+τ)|CX1(ti)]

(2)

(3)

式(1)，式(2)中，E[·]表示隨機變量的數學期望，還可以寫成如下形式

(4)

(5)

當采用正點觸發條件[16]，即

CX1(ti)=[α1σX1≤X1(ti)≤α2σX1,

(6)

式中：0≤α1<α2≤∞，此時，由式(4)和式(5)可得：

(7)

(8)

現在來討論多個自由度線性系統的情形，n個自由度具有黏性阻尼系統的運動方程為

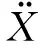
(9)

式中，M，C，K分別為結構的質量矩陣、阻尼矩陣和剛度矩陣。假設外力為均值為零的平穩高斯隨機過程，而質量、阻尼和剛度矩陣是確定的，則有RXXk是運動方程的齊次解，即有

(10)

(11)

式中：DXXk(τ)為隨機減量函數向量，引入標量反應過程Xk作為觸發條件的參考。從式(11)可以看出隨機減量函數DXXk(τ)為運動方程的齊次解。隨機減量函數可以按下式來估算：

(12)

由隨機減量法提取某一測點自由振動響應后，可以聯合特征系統實現算法(Eigensystem realization algorithm, ERA)進行結構模態參數識別。特征系統實現法是由結構自由響應識別結構模態參數的標準算法[17]，其利用系統脈沖響應函數構造廣義Hankel矩陣，利用奇異值分解技術，得到系統的最小實現，從而得到最小階次的系統矩陣，以此為基礎進一步識別系統的模態參數。

1.2基于隨機減量法分布式數據采集

Nagayama等[2]曾基于自然激勵技術(Natural Excitation Technique, NExT)提出的DDA方法基本原理如圖1所示。“節點1”為簇頭，負責為每個節點發送一個自由振動信號作為參考信號；而“節點2”到“節點ns”為傳感器節點，負責采集環境激勵下結構動力響應信號，計算自/互相關函數，并將相關函數傳遞給“節點1”，數據傳遞的總量為N·nd+N/2(ns-1)，其中N為時程記錄的總點數，nd為時程記錄平分的段數，ns為節點傳感器數目。一般來說，節點數越多，分布式數據采集方法比集中采集方法的高效性越明顯。受上述方法的啟發，Sim等[12]引入隨機減量技術，提出的一種分布式算法，具有更高的效率。該法數據采集和處理原理如圖2所示，與基于NExT技術的分布式數據采集方法相比，“節點2”到“節點ns”往“節點1”傳遞的不是自/互相關函數，而是隨機減量函數。因為該法發送的觸發條件通常比NExT法發送的自由振動時程信息短小，所以可以節省更多的數據傳遞帶寬和時間，基于隨機減量法的分布式采集方法具有更高的數據采集和處理效率。基于隨機減量法的分布式數據采集方法所需傳遞的數據量與觸發點的數目直接相關。對于正點觸發條件(式6)，觸發點的數目期望值為

(13)

式中：n(a1,a2)為介于a1和a2之間的觸發點數目；p(x)為X(t)的概率密度函數；Nx為X(t)中的點數；Nτ為隨機減量函數的點數。此時，需要傳遞的總數據點數為

(14)

圖1 基于NExT分布式數據采集

圖2 基于RDT分布式數據采集

1.3穩定圖確定模態階數

采用環境激勵下結構模態參數識別時，要求環境激勵必須滿足白噪聲。但實際結構的模態識別時，由于各種噪聲的影響，環境激勵往往不滿足白噪聲，因此引入穩定圖(Stabilisation Diagrams,SD)來消除虛假模態，提高模態參數的識別精度。穩定圖一般結合時域識別方法(例如ERA方法)進行，是基于系統階數敏感度分析的一種常用的系統極點辨別方法[3]。穩定圖法的基本原理是選用不同系統階數完成模態識別，通過鑒定系統極點對頻率、歸一化的振型、阻尼比的穩定性來判斷極點的真實性。通常穩定圖可輔助以功率譜密度函數進行模態判斷。傳統的穩定圖用于識別系統模態參數需要人的主觀判斷，容易產生誤差。

本文在基于模糊聚類算法的穩定圖繪制中以頻率為橫坐標，以系統階數為縱坐標，使每個極點包含兩個信息：頻率和系統階數，采用以下準則進行判斷，找到圖中聚類中心最近的數據點，這些數據點所對應的頻率及振型即為識別模態參數。本文采取的判據主要包括:① 當兩個模態的頻率差小于2 Hz時判定為一個模態；② 當沿著某個頻率的穩定圖譜線的極點數超過6時判定該頻率為真實頻率。

2 試驗驗證

2.1試驗模型

試驗模型是長度為2.438 4 m，寬度為0.914 4 m，一個兩短邊簡支的矩形彈性薄板，其厚度為0.019 05 m。制作板的材料是7層的膠合板層壓材料，主要物理性能指標如下：彈性模量為13 GPa，密度為485 kg/m3，泊松比為0.2。

2.2無線智能傳感器的網絡布置

采用自然激勵的方法，利用美國伊利諾伊大學香檳分校智能結構技術實驗室研制的ISM400型無線智能傳感器建立網絡系統，六個傳感器布置如圖3所示。ISM400型傳感器可以同時測量3個方向的加速度；可以測量溫度和濕度；用戶可以選擇采樣頻率和截斷頻率；可定制數字濾波器；內置4個通道的模擬數字轉換器，其中一個通道是專門為擴展應用所設計的，例如可以用于連接應變計來測量應變。

圖3 簡支板無線傳感器網絡布置方案

集中式算法以六個傳感器節點的全部加速度信息識別模型的振動特性。分布式算法按照不同的網絡拓撲情況分為三種工況。工況1由全部六個傳感器組成的網絡，其中S1為簇頭；工況2傳感器分成兩組，其中第一組傳感器由編號為S1，S2，S4，S5的四個傳感器組成，S1為簇頭，第二組傳感器由編號為S1，S3，S4，S6的四個傳感器組成，S3為簇頭；工況3傳感器分成兩組，其中第一組由編號S1，S2，S4，S5的四個傳感器組成，S1為簇頭，第二組由編號為S2，S3，S5，S6的四個傳感器組成的網絡，S3為簇頭。為保證兩組間傳感器相對的空間信息不致丟失，兩組傳感器中部分傳感器是重疊的。

2.3試驗數據采集和處理方法

數據采集和處理分別采用集中式和分布式兩種方法。數據處理流程如圖4所示，通過自然激勵法(NExT)從測試結構的響應信號中獲得自由響應信號，分別計 算自/互相關函數(對于集中式方法)和隨機減量函數(對于分布式方法)，然后運用ERA法提取系統的狀態空間參數，并結合穩定圖的方法剔除虛假模態，識別出精度較高的結構模態參數(固有頻率及模態振型)。兩種數據處理方法的主要區別是：集中式處理方法根據結構的響應信號計算自/互相關函數，然后基于相關函數進行模態參數識別；而分布式處理方法則先根據相關函數求得隨機減量函數，然后基于隨機減量函數進行模態參數識別。

圖4 數據采集處理流程

集中式數據采集處理方法，以六個節點的全部加速度信息得到的相關函數識別模型的振動特性。圖5為S1傳感器所采集的自然環境激勵下的結構動力響應信號。基于RDT的分布式數據采集處理方法，按照傳感器網絡拓撲三種工況，以隨機減量函數為基礎數據，識別模型的振動特性。限于篇幅，本文僅以傳感器S3的自隨機減量函數和S3關于S4的互隨機減量函數為例，其圖形見圖6。集中式數據采集方法需要傳遞的數據量為：61 440；三種工況下分布式數據采集方法需要傳遞的數據量依次為：6 144，3 454和3 454，占集中式算法傳遞數據的比例分別為10%，5.6%和5.6%。

圖5 豎向加速度響應信號(傳感器S1)

(a) S3-S3

(b) S3-S4

2.4試驗結果分析

對集中式和分布式算法，均引入穩定圖來消除虛假模態，提高模態參數的識別精度。集中式算法和分布式識別算法(工況1)時簡支板在環境激勵作用下的穩定圖，分別如圖7和圖8所示。圖中將頻率和階數分為六類，同時畫出頻率譜密度(PSD)曲線，十字表示數據輸入點，實心圓表示每一個聚類的中心，六個中心所對應的頻率及振型即為識別的模態參數。

根據分布式和集中式數據采集方法得到的數據識別的頻率見表1。表中相對誤差絕對值=(集中式算法識別頻率-分布式算法識別頻率(/集中式算法識別頻率。從表1中可以看出，分布式算法各種網絡拓撲工況下識別的頻率與集中式算法識別結果非常接近，三種工況下誤差最大值均發生在第3階頻率時，相對誤差分別為1.590 9%，1.604 5%和0.865 4%，其余工況下各階頻率相對誤差均小于1%，能滿足工程精度要求。

集中式和分布式算法得到的整體振型如圖9所示(為節省篇幅，僅給出分布式算法工況3下的識別模態振型圖)，分布式各種工況下振型與集中式算法下整體模態振型差別很小。引入模態置信度(Modal Assurance Criterion, MAC)來判斷振型的識別精度

(15)

式中：φZ表示分布式算法得到的振型；φq表示集中式算法得到的振型。MAC介于0到1之間，其值越接近于1，表示振型越準確。依據公式(15)，根據分布式算法得到的振型相對于集中式算法得到的振型的模態置信度MAC列在表2中。表中顯示三種工況下各階振型的MAC均大于0.8，除個別模態的MAC比較低，例如工況1和工況2下的第3階和第6階的MAC小于0.9，其余階振型均接近于1，分布式算法識別的模態可信。

圖7 簡支板環境激勵作用下穩定圖(集中式)

Fig.7 Stabilization diagram of simply supported plate through ambient excitation (Centralized processing)

圖8 簡支板環境激勵作用下穩定圖(分布式)

Fig.8 Stabilization diagram of simply supported plate through ambient excitation (Decentralized processing)

表1 簡支板頻率識別

3 結 論

本文提出了應用于分布式無線傳感器網絡的基于隨機減量技術分布式結構模態識別算法，并用該方法在實驗室簡支板模型上進行驗算。分布式數據采集處理方法不需要每個節點都與基站直接進行數據傳遞，可以大大減少數據傳遞所需要的時間和電池能量，而且因為各個組之間有重疊，很好的防止了傳感器之間相對空間信息的丟失。這種新的分布式算法本質上是分區、分級處理，允許傳感節點之間的交流和合作，并計及所測量的空間信息和局部信息。

(a) 一階振型(集中式)

(b) 一階振型(分布式)

(c) 二階振型(集中式)

(d) 二階振型(分布式)

(e) 三階振型(集中式)

(f) 三階振型(分布式)

(g) 四階振型(集中式)

(h) 四階振型(分布式)

(i) 五階振型(集中式)

(j) 六階振型(分布式)

(k) 六階振型(集中式)

(j) 六階振型(分布式)

模態階數123456工況10.99960.98910.81060.99020.99090.8835工況20.99980.98580.82850.87090.99410.8734工況30.99940.97060.99190.99510.99920.8985

與集中式算法識別結果的對比分析，可以得出以下結論：基于隨機減量法的分布式數據采集和模態識別方法得到的頻率和振型，與集中式數據采集方法得到識別結果吻合很好，頻率最大誤差1.6%，振型的模態置信度絕大部分都接近于1，表明該方法識別精度高，而且數據傳遞效率高，適合于密集布排傳感器網絡結構的振動測試，可以滿足工程應用。

[1] SIM S H, SPENCER JR B F. Decentralized strategies for monitoring structures using wireless smart sensor networks[R]. NSEL Report Series, No. 019, University of Illinois at Urbana-Champaign, U.S.A., 2010.

[2] NAGAYAMA T, SPENCER JR B F. Structural health monitoring using smart sensors[R]. NSEL Report Series, No.001, University of Illinois at Urbana-Champaign, U.S.A., 2007.

[3] 劉宇飛，辛克貴，樊健生，等. 環境激勵下結構模態參數識別方法綜述[J].工程力學，2014，31(4)：46-53.

LIU Yufei, XIN Kegui, FAN Jiansheng, et al. A review of structure modal identification methods through ambient excitation[J]. Engineering Mechanics, 214,31(4):46-53.

[4] PEETERS B, DE ROECK G. Reference-based stochastic subspace identification in civil engineering[J]. Inverse Problems in Engineering, 2000, 8: 47-7.

[5] 張敏，謝慧才，SIM S H, 等. 基于隨機子空間的分布式結構模態參數識別[J].深圳大學學報，2009，26(4)：394-399.

ZHANG Min, XIE Huicai, SIM S H, et al. Distribution modal identification based on stochastic subspace method[J]. Journal of Shenzhen University Science and Engineering, 2009, 26(4):394-399.

[6] 張敏，謝慧才，SIM S H, 等. 基于分布式傳感網絡的結構模態識別方法[J].土木工程學報，2010，43(3)：106-110.

ZHANG Min, XIE Huicai, SIM S H, et al. Modal identification technique based on distributed sensor networks[J]. China Civil Engieering Journal, 2010, 43(3):106-110.

[7] COLE H A． On-the-line analysis of random vibration[C]. AIAA / ASME 9th Structure, Structural Dynamics and Materials Conference, AIAA paper, 1968:268-288.

[8] COLE H A． Method and apparatus for measuring the damping characteristic of a structure[P]. United State Patent, No:3620069,1971.

[9] 陳德成，姜節勝． 隨機減量技術的方法與理論[J]．振動與沖擊，1984，3(4): 31-39.

CHEN Decheng, JIANG Jiesheng. Method and theory of random decrement technique[J]. Journal of Vibration and Shock, 1984,3(4):31-39.

[10] 劉劍鋒，李元兵，張啟偉. 基于改進隨機減量法和小波變換的結構模態參數識別[J]. 同濟大學學報，2015，43(10)：1447-1453.

LIU Jianfeng, LI Yuanbing， ZHANG Qiwei. Identification for modal parameters based on improved random decrement technique and wavelet transform[J]. Journal of Tongji University, 2015,43(10):1447-1453.

[11] 羅鈞，劉綱，黃宗明. 基于隨機減量法的非平穩激勵下模態參數識別[J]. 振動與沖擊，2015，34(21)：19-24.

LUO Jun, LIU Gang, HUANG Zongming. Modal parametric identification under non-stationary excitation based on random decrement method[J]. Journal of Vibration and Shock, 2015,34(21):19-24.

[12] SIM S H, CARBONELL-MARQUEZ J F, SPENCER JR B F, et al. Decentralized random decrement technique for efficient data aggregation and system identification in wireless smart sensor networks[J]. Probabilistic Engineering Mechanics, 2011,26:81-91.

[13] 黃方林，何旭輝，陳政清，等.隨機減量法在斜拉橋拉索模態參數識別中的應用[J].機械強度，2002，24(3):331-334.

HUANG Fanglin, HE Xuhui, CHEN Zhengqing, et al. Application of random decrement technique to modal parameter identification of cables for a cable-stayed bridge[J]. Journal of Mechanical Strength, 2002,24(3):331-334.

[14] VANDIVER J K，DUNWOODY A B，CAMPBELL R B，et al． A mathematical basis for the random decrement vibration signature analysis technique[J]． Transactions of the ASME Journal of Mechanical Design，1982，104: 307-313.

[15] BRINCKER R，KRENK S，KIRKEGAARD P H，et al． Identification of dynamical properties from correlation function estimates[J]．Bygningsstatiske Meddelllser，1992，63(1): 1-38.

[16] ASMUSSEN J C. Modal analysis based on the random decrement technique application to civil engineering structures[D]. Ph.D. thesis. Denmark: University of Aalborg, 1997.

[17] JUAN J N, PAPPA R S. An elgensystem realization algorithm (ERA) for modal parameter identification and model reduction[J]. Journal of Guidance Control and Dynamics, 1985, 8(5): 620-627.

Modalparametricidentificationofdistributiontypestructuresbasedonrandomdecrementtechnique

LU Jingzhou1， SIM, Sung Han2， SPENCER, B F, Jr.3

(1.School of Civil Engineering, Yantai University, Yantai 264005，China;2. School of Urban and Environmental Engineering, Ulsan National Institute of Science and Technology, Ulsan 44919, Korea;3. Department of Civil and Environmental Engineering, Illinois University at Urbana-Champaign, IL, 61801, USA)

Technology for partition processing and parallel analysis is essential to realize a dense array of wireless smart sensors network for measuring on large-scale civil structures. Here, a distributed data collecting approach for a system’s modal identification was proposed based on the random decrement technique (RDT). The performance of the RDT-based distributed data collecting was tested using a two-side simply supported plate model. Using ISM400 wireless smart sensors, the random decrement function was calculated with the measured vibration acceleration time histories of the plate by adopting the natural excitation technique (NExT). A time domain algorithm integrating NExT and the eigen-system realization algorithm (ERA) was applied to identify modal parameters of the plate and combined with the method of stability diagram (SD) to eliminate false modes. The identification results were compared with those based on the centralized method. It was shown that the plate’s modal shapes obtained with the proposed method are close to those obtained with the centralized method using the modal assurance criterion (MAC).

random decrement technique (RDT); distributed sensor networks; eigen-system realization algorithm (ERA); stabilization diagram (SD); modal identification

國家自然科學基金(51479174)

2016-04-20 修改稿收到日期：2016-06-27

逯靜洲 男,博士,教授,1973年12月

TU317

： A

10.13465/j.cnki.jvs.2017.17.008